基于压缩感知的语音盲稀疏重构算法及其去噪应用
李凤莲,畅江,张雪英,宋磊,田玉楚, 2
基于压缩感知的语音盲稀疏重构算法及其去噪应用
李凤莲1,畅江1,张雪英1,宋磊1,田玉楚1, 2
(1. 太原理工大学 信息工程学院,山西 太原,030024;2. 昆士兰科技大学 信息工程学院,澳大利亚 昆士兰,4001)
根据传统的正交匹配追踪(OMP)算法和稀疏度自适应匹配追踪(SAMP)算法各自的缺陷,提出可以在盲稀疏状态下重构带噪语音的多匹配正交追踪(MMOP)算法。该算法采用同时匹配多个原子以及同步增大和缩小原子集的办法来解决SAMP算法中原子的过匹配和欠匹配现象,此外,还提出一种新的去噪思想和设置初始步长方法,并且采用分阶段步长来重构原始语音信号。研究结果表明:本文算法不仅修正SAMP算法的过匹配和欠匹配的现象,而且还具有匹配速度快、迭代次数少的优点,同时又提高语音信号在盲稀疏状态下的重构精度,此外,该算法还可以应用在噪声语音中,有较明显的去噪效果,且其重构后的语音主客观质量评价都要好于传统的OMP算法和SAMP算法。
压缩感知;重构算法;语音去噪;匹配追踪算法
由于重构算法是压缩感知[1−2](compressed sensing, CS)理论研究的关键技术之一,因此,近年来,国外的学者对CS的重构算法进行大量研究,国内的一些学者也开始陆续对CS重构算法进行相关研究,例如王良君等[3]提出在多稀疏空间下重构图像,何宜宝等[4]提出利用概率结构模型实现信号重构,王超等[5]提出基于稀疏约束的自适应正则化迭代重构算法、陈胜垚等[6]提出混沌压缩感知的在线估计,王娟[7]提出基于量子免疫的CS重构算法。虽然已有的算法很多,但没有一个算法是普遍适用的,很多算法也都是在经典的CS重构算法之上进行改进,例如刘记红等[8]提出基于改进的正交匹配追踪算法,Do等[9]提出稀疏度自适应的匹配追踪算法,高睿等[10]提出的变步长匹配追踪算法。目前,最具有代表性的经典CS重构算法有基追踪法(basis pursuit, BP)[11]、正交匹配追踪(orthogonal matching pursuit, OMP)[12]以及稀疏度自适应匹配追踪(sparsity adaptive matching pursuit,SAMP)[13]等算法。然而,对于现有的OMP算法和SAMP算法都各有其优缺点。OMP算法是最常用的一种算法,虽然重构精度高,但它是在稀疏度已知的情况下才可使用,若稀疏度未知,则就要对其进行估计,稀疏度估计的过高和过低都会影响重构后的精度和速度。SAMP算法是一种稀疏度自适应的匹配追踪算法,它虽然可以在盲稀疏度的情况下对信号进行重构,但是它以降低算法的运算速度为代价来进行盲匹配的。此外,SAMP算法还存在过匹配和欠匹配[14]现象,该现象影响程序运行时的速度、精度以及稳定性。基于上述原因,本文作者针对语音信号,提出一种可以重构盲稀疏带噪语音的多匹配正交追踪算法(multi-matching orthogonal pursuit,MMOP),该算法使传统的压缩感知过程在3个方面进行了改进,首先它解决了SAMP算法的过匹配和欠匹配问题,并且还简单有效地完成了对初始步长的估计,加快了算法的计算速度;其次,它采用分阶段步长的思想来加强算法的重构精度,最后又提出一种新的方式来滤除原始信号中的噪声。通过这3方面的改进方法,使得语音信号达到了更清晰和更准确的重构效果。
1 压缩感知
1.1 压缩感知理论
在对信号进行观测时,若×维的观测矩阵与不相关,且<<<,为×1维的列向量,则信号的观测值为
在对信号进行重构时,实际上就是对式(2)求逆运算的过程,根据<<<,可将该逆运算转化为1或0范数优化问题,若采用0范数求解,只要求出中的个稀疏值即可,即求解公式(4)中的。
在CS理论中,通常使用的重构算法是基于0范数[12−13]优化的OMP算法和SAMP算法。
1.2 OMP算法和SAMP算法存在的问题和不足
正交匹配追踪(OMP)算法是一种常用的贪婪追踪算法,它的基本思想是:采用贪婪迭代的方法来达到原子选择和残差更新的目的,在每次迭代中对已选原子集合进行正交化处理,并计算求得观测矩阵与当前残差的相关性,找出最相关的原子用最小二乘法进行信号的稀疏逼近,求出残差,再重复之前的操作,完成次迭代,其中迭代的次数就为信号的稀疏度。OMP算法能够以极高的概率重构原始信号,但该算法实现的前提条件是所需信号的稀疏度必须是已知的,若能够精准地确定信号的稀疏度,则采用OMP算法重构原始信号是非常快速和有效的,而在实际情况中,信号经压缩传输后其稀疏度一般都是无法知晓的,尤其对于语音信号而言,经过分帧处理后的语音,其每一帧的稀疏度都是不一样的,因此,语音信号的稀疏度就更无法确定。
SAMP算法是OMP算法的一种改进算法,它通过设置1个初始步长,在程序反复迭代的过程中更新,找出最优原子,实现信号的稀疏估计,因此,该算法具有重建盲稀疏信号的优点。然而,该算法仍然存在一些问题,首先由于该算法迭代步骤增加,程序运行时需要花费大量的时间;其次,该算法在迭代过程中,过分依赖初始步长,若初始步长估计错误可导致程序运行时间过长;再次,该算法的迭代终止条件是当前残差小于设定阈值,由于不能保证每次的残差都会小于上一次的残差,因此,这样的终止条件极容易使信号在重构时产生过匹配和欠匹配的现象,从而降低了信号的重构精度和重构效率。
2 多匹配正交追踪算法(MMOP)
2.1 MMOP算法的基本原理
基于传统OMP算法和SAMP算法所存在的不足,本文提出一种MMOP算法,该算法的基本原理是在程序运行时的每次迭代中,从观测矩阵与当前残差的内积中选择与本次循环最相关的前个原子作为候选集,式(6)为其相关系数的表达式:
根据相关系数选出候选集原子后,再把本次候选集的原子和上次候选集的原子合并为新的候选集,将新选出的原子,用最小二乘法进行多匹配得出重构信号,求出当前残差。式(7)为用最小二乘法估计原始信号,式(8)为残差的求解公式:
1=+(9)
2=−(10)
式中:为信号迭代步长,然后比较候选集长度为1和2的残差,选用残差最小的候选集个数为当前,进行下一次迭代,当残差小于某个预先设定好的精度后程序将自动停止迭代。每次迭代完成后其就是语音信号每一帧的稀疏度。
2.2 MMOP重构中的阈值去噪思想
目前已有研究成果指出应用压缩感知理论可以提高原始信号的抗噪性能[15−18],但只能是在噪声强度不大的情况下,通过设置式(4)的阈值来限制重构的稀疏个数,再利用式(5)进行重构去噪,但是,由于重构的语音本身就是带噪的语音信号,所以,若原始信号的噪声比较大,最终重构出的信号仍是噪声信号,因此,传统的压缩感知理论不能达到真正的去噪目的[19]。基于上述原因本文所提出的这种阈值去噪思想可以使语音信号在无噪声状态时,直接跳过无语音帧,对有语音帧进行重构,而在语音信号含有噪声时,使带噪语音信号得到清晰的重构,其基本原理如下。
假设带噪语音为
式中:z,z和z分别为经过频域变换后的带噪信号、纯净信号和噪声信号。带噪语音在变换域上的稀疏表示为
式(13)为信号帧在有语音时的去噪过程,噪声阈值的设置方式为无语音期间信号帧的稀疏个数。为了满足语音信号的自适应重构要求,本文对噪声阈值进行2步评估,即设置2个去噪阈值,分别为初始阈值和迭代后的阈值。初始阈值的设置方式由重构纯净语音时的实验得出,若纯净语音在固定的帧长中,其无语音帧的稀疏个数一般总是小于某个范围,而这个范围就设定为初始去噪阈值,当为含噪语音时,若某个帧重构后的稀疏个数大于但远小于之前某个重构好的语音帧时,则可以判定该段语音信号帧为噪声帧,就将该段语音帧的稀疏个数设为。此设计方案可以有效地滤除噪声,实现语音增强的功能。
2.3 MMOP算法的分阶段步长思想
为了提高重构算法的速度,MMOP算法采用分阶段步长的法方法来重构语音信号。由于本文算法设置了一个去噪声阈值,若≤,则在重构过程中是不进行任何处理的,信号直接置零,这就说明每一个语音帧的稀疏个数至少要大于这个噪声阈值,即≥,因此,就可以设置MMOP的初始步长=。该方法简单而有效地实现了对初始步长的估计。此外,研究表明[10],在每次迭代过程中,当还没有达到所需重构信号的稀疏个数时,相邻2次迭代的残差是逐步减小的,而且随着迭代速度的增加,此残差的下降速度越来越慢。因此,在匹配速度变慢时,采用减小迭代步长的方法来逼近信号的稀疏度,信号迭代步长的增加量减小为=×(其中,为信号的压缩比)。
2.4 MMOP的具体实现步骤
步骤1:将带噪语音进行分帧加窗后,将每一帧的原始信号直接投影到观测矩阵上,得到信号的观测值。
步骤3:根据式(6)计算出相关系数,并从中选择个最大相关系数存入中。
步骤4:合并当前候选集与前一次候选集作为新的候选集new,更新=new,中的原子个数为新的,利用式(7)和(8)求出信号的当前估计值和当前 残差。
步骤5:当迭代次数=1时,求出new中不为零的原子个数,若不为零的原子个数=,则可认为该帧语音为有语音信号,转入步骤6;否则可认为该帧语音为无语音信号,设置当前帧为零,并进行下一帧的信号重构,=+1,转入步骤3。
步骤8:求出当前中不为零的原子个数K,若,则可认为该帧语音为噪音信号,更新噪声阈值,求出该帧的噪声功率谱,同时更新噪声功率,根据得到去噪后的语音帧,并进行下一帧的信号重构,转入步骤3;否则,无需更新噪声阈值,直接转入步骤3。
3 实验结果及分析
本实验所选用的语音库为英语语音库,在该语音库中,分别选取男生和女生的语音各20句,每段语音的时长为2 s,对于每段语音的每个实验,都重复5次,结果取其平均值。实验所用的仿真软件为MATLAB,实验方法是对每段语音采用OMP,SAMP和MMOP这3种算法进行重构,并比较它们重构后的语音质量。其中OMP算法是在已知语音信号每一帧稀疏度的情况下进行的,SAMP算法采用的固定迭代步长为4。实验中采用信噪比和主观质量评价(PESQ)的方法作为重构语音信号的评价标准。其中信噪比(SNR)的计算公式为
式中:s为信号功率;n为噪声功率。实验中语音信号的帧长为512个样点。实验分别讨论2种情况:一种是在无噪声条件下,分析这3种算法的重构性能;另一种情况是在有噪声的条件下,分析SAMP阈值去噪方法与MMOP去噪方法的去噪效果。
实验1:考察无噪声语音在不同压缩比的状态下,使用不同方法重构以后,语音的质量情况。表1所示为采用不同方法重构语音后的信噪比SNR和PESQ。
从表1可以看出:当小于0.3时,由于OMP算法的计算复杂度低,能够在较少数据中快速、准确找出最相关的匹配原子;而当大于0.3时,SAMP算法不论从信噪比还是PESQ都比OMP算法的重构效果好。对于本文所提出的MMOP算法,当压缩比不同时,其重构后语音的信噪比以及PESQ全都比OMP算法和SAMP算法的高。
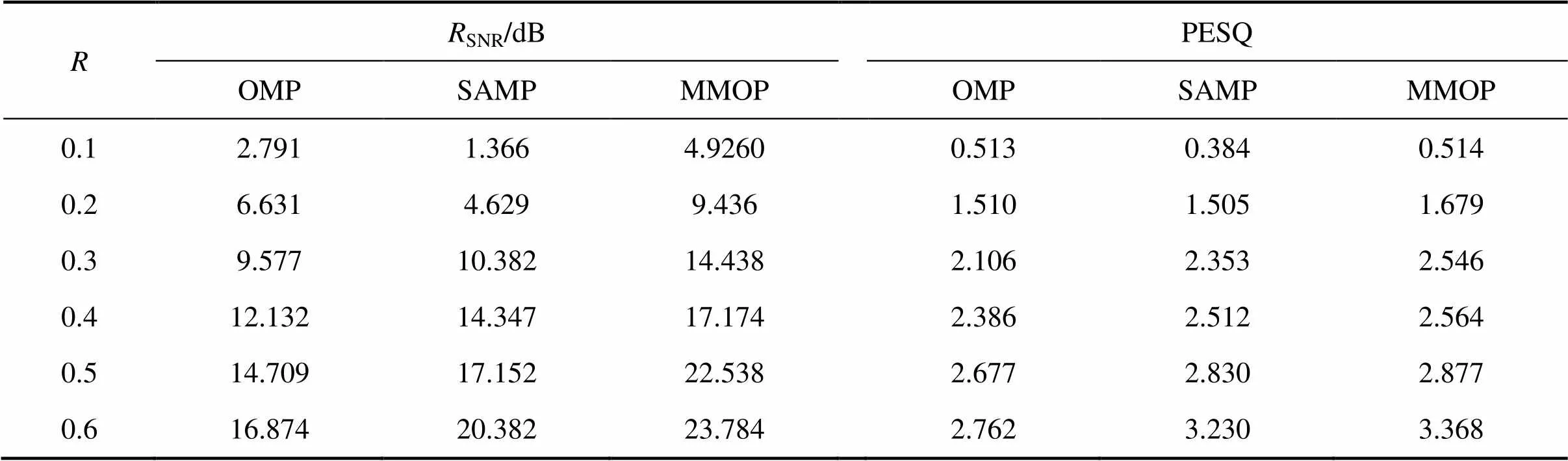
表1 采用不同方法重构语音后的RSNR和PESQ
由于MMOP所选取的迭代步长为自适应的,对于不同的语音帧,算法的迭代次数是不一样的,因此很难精确地计算出该算法的时间复杂度。所以,为了对这3种算法的计算速度进行分析,本文对算法的迭代次数和算法的运行时间进行比较,结果如表2和图1所示。对于重构2 s的语段来说,从表2可以看出MMOP算法的迭代次数要比OMP算法和SAMP算法的少得多,这是因为MMOP算法采用分阶段步长的方法根据实际的语音情况自适应调整迭代步长,从而大大减少了迭代次数。对于图1来说,OMP算法的程序运行时间要比SAMP算法快很多,甚至在10 dB为0.6时,SAMP算法所要耗费的时间几乎是OMP算法的6倍,这是因为SAMP算法迭代步长固定,且每增加1次迭代算法的运算量就比前一次大,所以,即便SAMP算法的重构效果较好,迭代次数少,但其计算速度慢的缺点就阻碍了该算法的应用。而OMP算法之所以能够快速准确地重构,是因为其稀疏度为已知确定的,但在实际情况中,语音信号每一帧的稀疏度都是未知的,所以,采用OMP算法就不能对信号进行快速准确的重构。本文提出的MMOP算法在运行速度上虽然不及已知稀疏度的OMP算法运法速度快,但是比起SAMP算法,其速度已有明显提高。

表2 每种算法的平均迭代次数
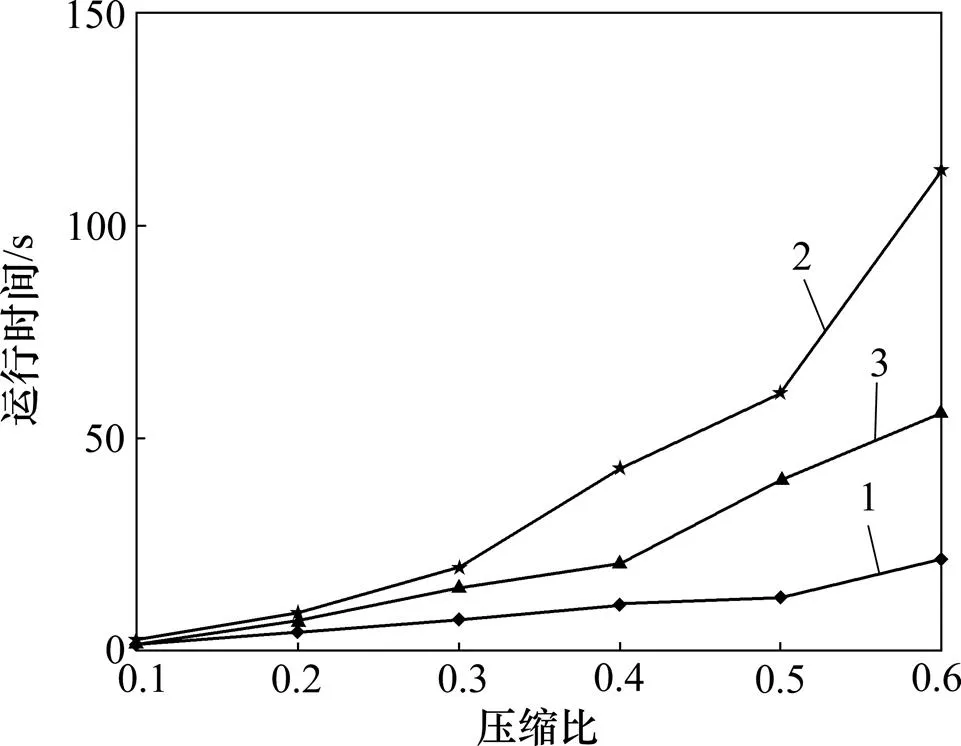
1—SAMP;2—OMP;3—MMOP
图1 不同算法的运行速度对比
Fig. 1 Running speed of different algorithms
图2所示为将这3种重构算法的相对误差和进行了比较。从图2可以看出:当压缩比大于0.3时,SAMP算法的相对误差较小,而本文的MMOP算法重构的语音,其相对误差都比前2种算法的小;当压缩比小于0.3时,MMOP的相对误差明显比OMP算法和SAMP算法的小,这表明在压缩比很大的情况下,采用MMOP算法可以使原始信号得到更精确的重构。
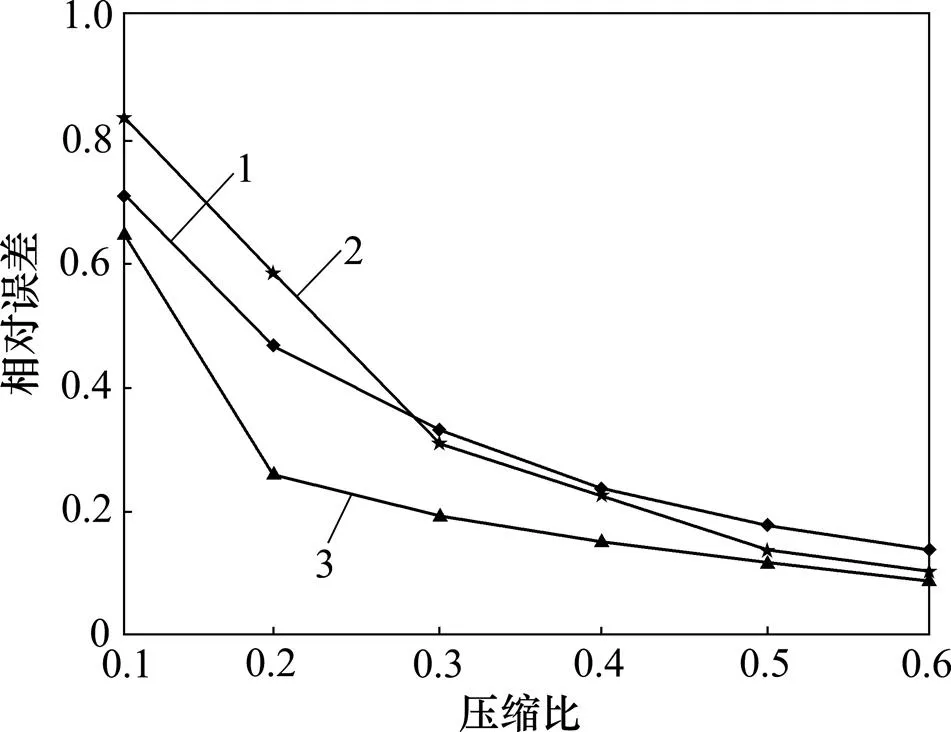
1—SAMP;2—OMP;3—MMOP
图2 不同算法的相对误差对比
Fig. 2 Comparison of relative error of different algorithms
图3所示为当压缩比为0.5时采用这3种方法对某段语音重构后的效果图。从图3可以看出:SAMP算法重构后的语音信号在横坐标为2×104处与原始语音信号有明显不一致的地方,并且该处的幅值明显比原始信号的大,这是一种“过匹配现象”。此外,还有一种现象为“欠匹配现象”,该现象在图中不容易被直接看出。从图3还可以看出本文的MMOP算法可以很好地解决重构过程中的过匹配和欠匹配问题,并且结合表1,可以看出它的重构效果要比OMP和SAMP算法的要好。
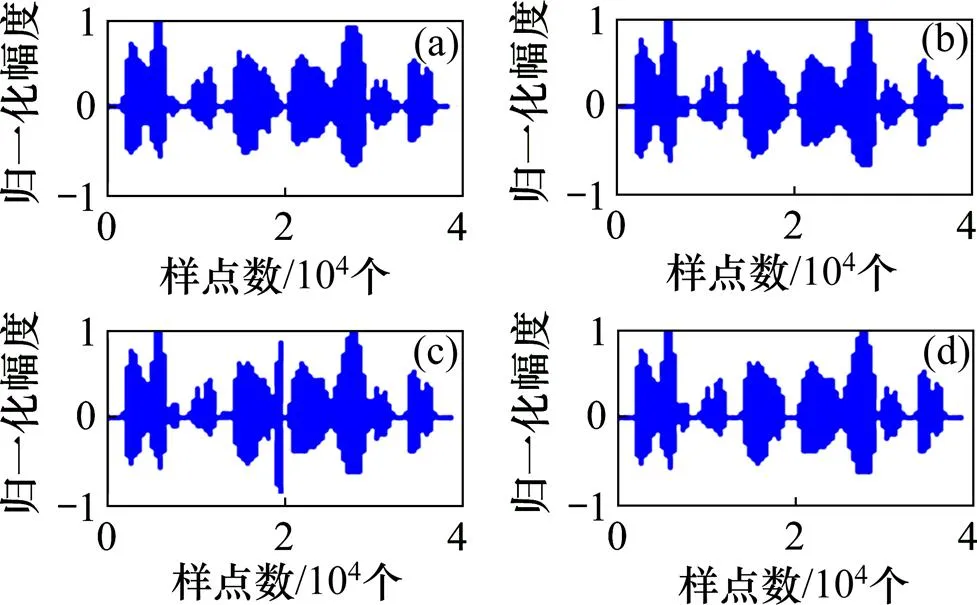
(a) 原始语音;(b) OMP重建语音;(c) SAMP重建语音;
(d) MMOP重建语音
图3=0.5时不同方法的重建效果图
Fig. 3 Reconstruction effect of different method when=0.5
实验2:考察信号在有噪声的情况下,比较传统SAMP算法的阈值去噪效果和本文所提出的MMOP算法的阈值去噪效果。图4所示为当带噪语音信噪比为5 dB时的去噪效果图。表3所示为当压缩比固定=0.3时,在不同噪声强度下,采用MMOP算法进行语音去噪以后的SNR和PESQ。表4所示为当原始含噪语音的信噪比为10 dB时,在压缩比不同的情况下MMOP算法的去噪性能。

(a) 原始语音;(b) 含噪语音;(c) SAMP阈值去噪;
(d) MMOP算法去噪
图4SNR为5 dB时MMOP的去噪效果图
Fig. 4 MMOP de-noising effect atSNRof 5 dB
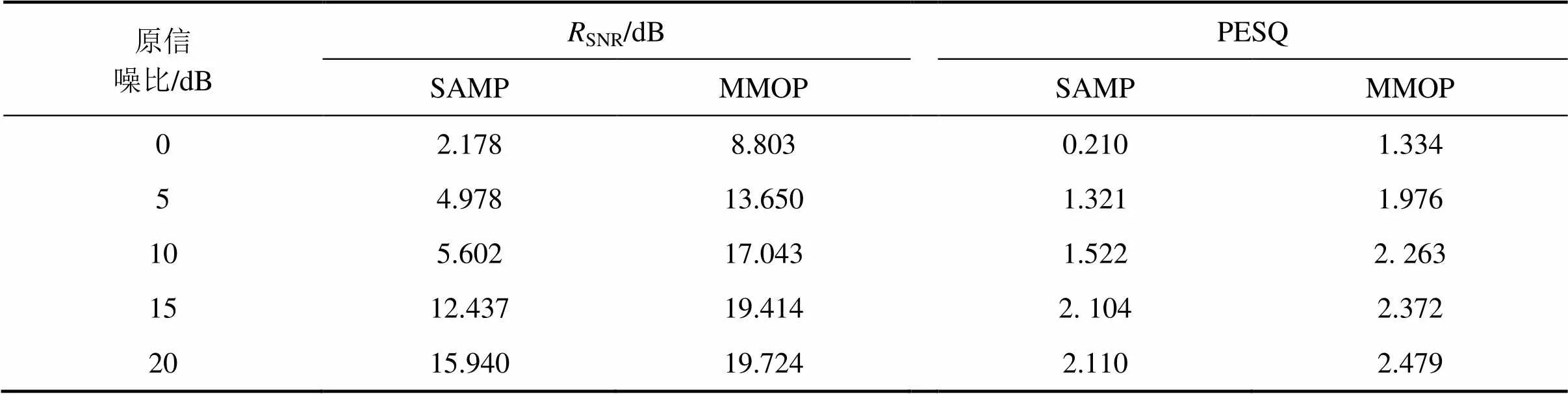
表3 R=0.3时SAMP和MMOP的去噪效果
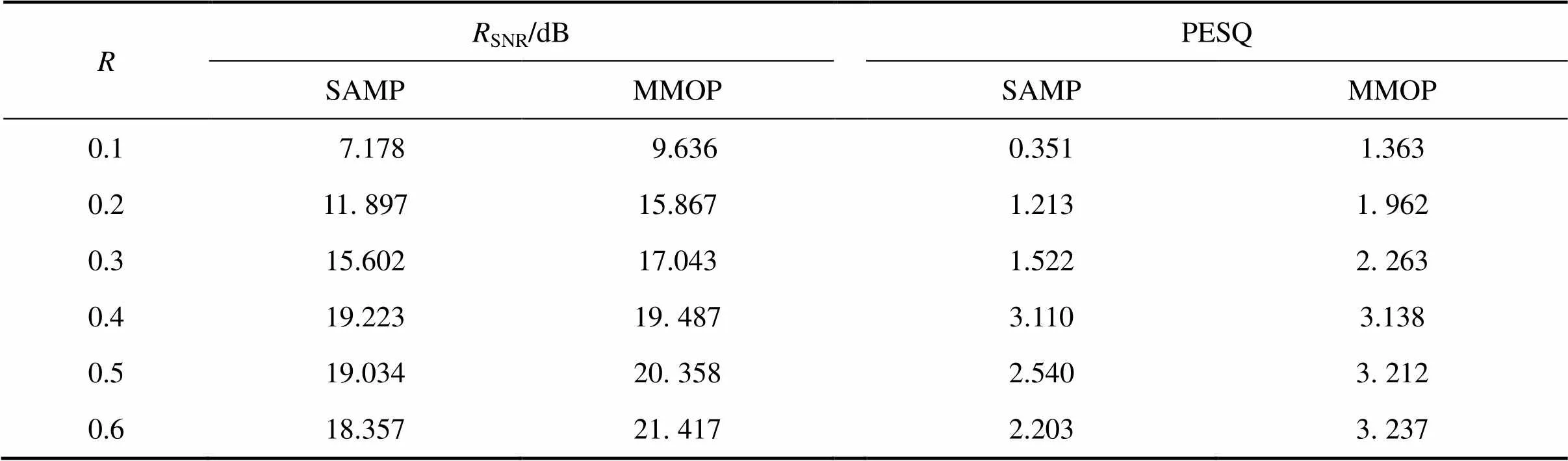
表4 原噪声比为10 dB、压缩比不同时MMOP的去噪效果
在本实验中,其噪声信号均采用高斯白噪声,这是因为实际的噪声信号经白化及同态滤波处理后都可以转化为高斯白噪声。从图4可以看出:将原始信号加上白噪声以后,通过设置噪声阈值的方式采用传统SAMP算法只能去除无语音期间的噪声,但是在有语音期间其重构后的语音仍是带噪语音,而使用MMOP算法,通过对噪声阈值的两步评估以及对含噪语音采用功率相减的方法,不仅可以滤除无语音期间的噪声,而且可以明显地去除有语音期间的噪声。
从表3可以看出:当压缩比固定=0.3时,相比于SAMP算法,MMOP算法有更好的去噪效果。当带噪语音的信噪比小于10 dB时,MMOP算法的去噪能力要比SAMP算法的去噪能力更强,并有相对较高的信噪比SNR和PESQ;当带噪语音大于15 dB时,由于背景噪声减弱,每种算法的去噪效果并不明显。
从表3可以看出:当原噪声信噪比为0.4时,SAMP算法的去噪效果最好,而当原噪声的信噪比大于0.3时,它的去噪效果下降。这是因为压缩比变大时,在重构时就会重构出一部分噪声,由此看出SAMP算法不能达到真正的去噪目的。对于MMOP算法,它不受压缩比的束缚,摆脱了压缩感知去噪方法的局限性。由表4可知:在相同的噪声干扰下,MMOP算法的去噪效果也要比SAMP算法的好。
4 结论
1) 针对使用传统压缩感知在处理语音信号时存在的一些问题,本文提出了3种改进算法,分别改进了重构算法的过匹配和欠匹配问题、重构过程中的初始步长设置问题和匹配速度问题以及重构时的去噪 问题。
2) 虽然本文结合语音信号,对已有的压缩感知理论进行相关改进,但是基于语音信号自身的特点,如何使用感知理论对语音信号进行有效处理,使其可以更为准确和快速地重构出来,还需要不断地研究和 完善。
[1] Donoho D. Compressive sampling[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289−1306.
[2] Donoho D L, Tsaig Y. Extension of compressed sensing[J]. Signal Processing, 2006, 86(3): 533−548.
[3] 王良君, 石光明, 李甫, 等. 多稀疏空间下的压缩感知图像重构[J]. 西安电子科技大学学报(自然科学版), 2013, 40(3): 88−97.
WANG Liangjun, SHI Guangming, LI Fu, et al. Compressed sensing image reconstruction in multiple sparse spaces[J]. Journal of Xidian University (Natural Science), 2013, 40(3): 88−97.
[4] 何宜宝, 毕笃彦. 利用概率结构稀疏模型实现信号重构的新算法[J]. 西安电子科技大学学报(自然科学版), 2013, 40(2): 235−241.
HE Yibao, BI Duyan. Signal reconstruction algorithm based on probabilistic structured sparse model[J]. Journal of Xidian University (Natural Science), 2013, 40(2): 235−241.
[5] 王超, 闫镔, 李磊, 等. 基于稀疏约束的自适应正则化迭代重建算法[J]. CT 理论与应用研究, 2012, 21(4): 689−698.
WANG Chao, YAN Bin, LI Lei, et al. An adaptive regularization iterative reconstruction algorithm on the basis of a sparse constraint[J]. CT Theory and Applications, 2012, 21(4): 689−698.
[6] 陈胜垚, 席峰, 刘中. 基于混沌压缩感知的稀疏时变信号在线估计[J]. 电子与信息学报, 2012, 34(4): 838−843.
CHEN Shengyao, XI Feng, LIU Zhong. Online estimation of sparse time-varying signalswith chaotic compressive sensing[J]. Journal of Electronics & Information Technology, 2012, 34(4): 838−843.
[7] 王娟. 量子免疫克隆算法研究及在压缩感知重构中的应用[D]. 南京: 南京邮电大学信号与信息处理学院, 2012: 5−60.
WANG Juan. Quantum-inspired immune clonal algorithm and its application to compressed sensing reconstruction[D]. Nanjing: Nanjing University of Posts and Telecommunications. School of Signal and Information Processing, 2012: 5−60.
[8] 刘记红, 黎湘, 徐少坤, 等. 基于改进正交匹配追踪算法的压缩感知雷达成像方法[J]. 电子与信息学报, 2012, 34(6): 1344−1350.
LIU Jihong, LI Xiang, XU Shaokun, et al. Compressed sensing radar imaging methods based on modified orthogonal matching pursuit algorithms[J]. Journal of Electronics & Information Technology, 2012, 34(6): 1344−1350.
[9] Do T T, Gan L, Nguyen N, et al. Sparsity adaptive mating pursuit algorithm for practical compressed sensing[C]// Asilomar Conference on Signals, Systems and Computers. Pacific Grove, California, 2008: 581−587.
[10] 高睿, 赵瑞珍, 胡绍海. 基于压缩感知的变步长自适应匹配追踪重建算法[J]. 光学学报, 2010, 30(6): 1639−1644.
GAO Rui, ZHAO Ruizhen, HU Shaohai. Variable step size a daptive matching pursuit algorithm for image reconstruction base don compressive sensing[J]. Acta Optic Sinica, 2010, 30(6): 1639−1644.
[11] Aybat N S, Iyengar G. A first-order augmented Lagrangian method for compressed sensing[J]. SIAM Journal on Optimization, 2012, 22(2): 429−459.
[12] Sun H, Ni L. Compressed sensing data reconstruction using adaptive generalized orthogonal matching pursuit algorithm[C]// 2013 3rd International Conference on Computer Science and Network Technology (ICCSNT). Dalian, China: IEEE, 2013: 1102−1106.
[13] Chi Y J, Scharf L L, Pezeshki A. Sensitivity to basis mismatch in compressed sensing[J]. IEEE Transactions on Signal Processing, 2012, 59(5): 2182−2195.
[14] 朱延万, 赵拥军, 孙兵, 等. 一种改进的稀疏度自适应匹配追踪算法[J]. 信号处理, 2012, 28(1): 80−86.
ZHU Yanwan, ZHAO Yongjun, SUN Bing, et al. A modified sparsity adaptive matching pursuit algorithm[J]. Signal Processing, 2012, 28(1): 80−86.
[15] BAO Guangzhao, YE Zhongfu, XU Xu, et al. Approach to blind separation of speech mixture based on a two-layer sparsity model[J]. IEEE Transactions on Audio Speech and Language Processing Sensing Compressed, 2013, 21(5): 899−906.
Central South University of Technology, 2013, 20(3): 702−714.
[17] 孙林慧, 杨震. 基于自适应基追踪去噪的含噪语音压缩感知[J]. 南京邮电大学学报(自然科学版), 2011, 31(5): 1−6.
SUN Linhui, YANG Zhen. Compressed sensing of noisy speech signal based on adaptive basis pursuit de-noising[J]. Journal of Nanjing University Posts and Telecommunications (Natural Science), 2011, 31(5): 1−6.
[18] 成经士. 压缩感知理论在语音信号去噪中的应用[J]. 现代电子技术, 2012, 35(7): 84−88.
CHENG Jingshi. Application of compressed sensing theory in speech denoising[J]. Modern Electronics Technique, 2012, 35(7): 84−88.
[19] Jeon Y Y, Lee S M. A speech enhancement algorithm to reduce noise and compensate for partial masking effect[J]. Journal of Central South University of Technology, 2011, 18(4): 1121−1127.
Reconstruction algorithm of blind sparse and its de-noising application in speech based on
LI Fenglian1, CHANG Jiang1, ZHANG Xueying1, SONG Lei1, TIAN Yuchu1, 2
(1. College of Information Engineering, Taiyuan Universi ty of Technology, Taiyuan 030024, China;2. Faculty of Information Technology, Queensland University of Technology, QLD 4001, Australia)
Considering the defects of the traditional orthogonal matching pursuit (OMP) algorithm and the sparsity adaptive matching pursuit (SAMP) algorithm, the multi-matching orthogonal pursuit (MMOP) algorithm was proposed under the condition of blind sparse with noise speech. The proposed algorithm used method of the match more than one atom to solve the over matching and less matching problems of SAMP algorithm as well as method of growing and shrinking atomic set. In addition, a new method of speech de-noising and the initial step, and the phased step was also proposed to reconstruct the original speech signal. The results show that the proposed algorithm can not only solve the SAMP algorithm problem of over matching and less matching, but also improve the matching speed and lessen the iterations number, and at the same time improve the accuracy of reconstruction. What’s more, the proposed algorithm can also be applied to the common noisy speech, with a better speech quality evaluation than the traditional OMP algorithm and SAMP algorithm.
compressed sensing; reconstruction algorithms; speech de-noising; matching pursuit algorithm
TN921.3
A
1672−7207(2015)01−0164−07
2014−02−22;
2014−04−17
国家自然科学基金资助项目(61371193);山西省自然科学基金资助项目(2012011014-1);山西省青年科技研究基金资助项目(2013021016-2);山西省回国留学人员科研基金资助项目(2013-034) (Project(61371193) supported by the National Natural Science Foundation of China; Project(2012011014-1) supported by the Natural Science Foundation of Shanxi Province; Project(2013021016-2) supported by the Natural Science Foundation for Young Scientists of Shanxi Province; Project(2013-034) supported by the Shanxi Provincial Foundation for Returned Scholars)
张雪英,教授,博士生导师;从事语音信号处理、音频水印、煤矿安全预警及信息化研究;E-mail: tyzhangxy@163.com
10.11817/j.issn.1672−7207.2015.01.023
(编辑 杨幼平)

