一种基于稠密SIFT特征对齐的稀疏表达人脸识别算法

周 全 魏 昕 陈建新 郑宝玉



一种基于稠密SIFT特征对齐的稀疏表达人脸识别算法

周 全*魏 昕 陈建新 郑宝玉

(南京邮电大学宽带通信与传感网技术教育部重点实验室 南京 210003)

该文针对人脸图像受到非刚性变化的影响，如旋转、姿态以及表情变化等，提出一种基于稠密尺度不变特征转换(SIFT)特征对齐(Dense SIFT Feature Alignment, DSFA)的稀疏表达人脸识别算法。整个算法包含两个步骤：首先利用DSFA方法对齐训练和测试样本；然后设计一种改进的稀疏表达模型进行人脸识别。为加快DSFA步骤的执行速度，还设计了一种由粗到精的层次化对齐机制。实验结果表明：在ORL, AR和LFW 3个典型数据集上，该文方法都获得了最高的识别精度。该文方法比传统稀疏表达方法在识别精度上平均提高了4.3%，同时提高了大约6倍的识别效率。

人脸识别；人脸对齐；稠密尺度不变特征转换特征；稀疏表达模型

1 引言

作为高层视觉的主要任务之一，人脸识别的目的是区分输入人脸图像的类别信息。人脸识别技术不仅是计算机视觉领域的研究热点，而且为相关的实际应用提供技术支持，如：人脸鉴定[3]，人机交互[4]，视频监控[5]以及入侵检测[6]等。过去十几年来，学者们设计了很多成功的人脸识别系统。从建模的角度出发，现有的人脸识别方法大致可以分为两个类别：监督式模型和非监督式模型。监督式模型通过判别准则来识别人脸，如线性映射模型[12]和线性回归模型[13]等。实际的人脸图像经常受到剧烈的变形和噪声干扰，如光照，遮挡，旋转、姿态和表情变化等，限制了这类方法在实际中的应用。非监督式模型则主要采用图像重建的方法来建模，并通过重建误差来估计人脸类别。比较经典的建模方法包括主成份分析(Principal Component Analysis, PCA)[14]，独立成份分析(Independent Component Analysis, ICA)[15]和稀疏表达模型(Sparse Representation Models, SRMs)等。PCA方法也称为特征脸方法，通过最大化所有训练样本的散度来计算主要的投影方向。ICA方法是PCA方法的扩展，通过求取一系列相互独立的投影方向，然后将训练样本投影到由这些投影方向张成的特征空间中[15]。SRM模型[16]广泛应用于正脸样本的识别，在提高识别精度的同时很好地解决了遮挡，光照以及噪声对人脸图像识别的影响。Peng等人[17]提出了一种改进的稀疏表达模型，专门用来处理刚性变换下的非正脸图像的识别问题。Wagner等人[18]在Peng等人[17]的研究基础上，提出一种面向实际应用的人脸识别系统。但在实际场景中，无论是训练图像还是测试图像，都会受到非刚性变换的影响，如旋转、表情、姿态等的变化，这就需要研究非刚性变换作用后人脸图像的识别问题。

本文提出一种基于稠密SIFT(Scale Invariant Feature Transform)特征对齐(Donse SIFT Feature Alignment, DSFA)的稀疏表达人脸识别算法。首先将训练图像向测试人脸对齐，然后利用稀疏近似的方法进行人脸识别。具体而言，首先提取图像每个像素的SIFT特征描述子[19]，然后根据图像对齐准则建立图像对齐模型。在对齐模型的优化过程中，设计一种由粗到精的层次化对齐机制，可大大降低算法复杂度。最后，设计一种改进的稀疏表达模型来进行人脸识别。本文方法不需要测试人脸是正脸图像，提高了整个算法的灵活性。文献[18]提出的SRM模型与本文方法直接相关，但两者在方法动机和技术细节上存在本质不同。首先，两种方法的假设前提不同。文献[18]中假设测试图像是一系列非对齐人脸图像，而训练图像是一系列对齐的正脸图像。本文则考虑在训练和测试图像都是非对齐人脸图像，并都受到非刚性形变情况下的人脸识别问题。其次，两种方法的工作机制不同。文献[18]是测试图像向训练图像对齐，而本文方法是训练图像向测试图像对齐。最后，两种方法在具体算法上不同。文献[18]采用线性迭代更新的方法求取一系列最优的刚性变换，将测试人脸图像对齐到训练图像，而本文运用DSFA算法作为一种非刚性变换将训练图像对齐到测试图像。与传统的人脸识别算法和现有的SRM模型相比，实验结果证明了本文方法获得了更高的识别精度和更快的识别速度。总而言之，本文主要贡献如下：(1)针对人脸图像易于受到非刚性变换的影响(如旋转、姿态和表情变化等)，设计了一种DSFA算法进行人脸对齐；(2)为提高DSFA的优化效率，设计了一种由粗到精的层次化对齐机制；(3)得到大致对齐的训练样本图像之后，设计了一种改进的SRM模型，并提出一种易于实现的识别算法。

2 基于DSFA的人脸图像对齐

2.1 稠密SIFT特征描述子提取

SIFT特征[19]是一种刻画图像梯度变化信息的鲁棒性描述子，并广泛应用于人脸识别[20]。计算SIFT特征主要包括特征点检测和特征点描述两个过程，本文只采用特征点描述过程。以像素=(,)为中心，将16×16大小的图像区块分割成4×4个较小的区块(每个区块的大小为4×4)。在每个4×4区块中统计8个方向上的梯度直方图。这样像素就可以表示成为一个4×4×8=128维度的特征向量。稠密SIFT特征描述子提取就是对图像中每个像素都提取SIFT特征描述子。

2.2人脸图像对齐模型及其优化

给定两幅人脸图像1和2，图像对齐的目的就是希望图像1中像素经过漂移之后，在图像2中具有相同或者类似的SIFT特征。定义()=((),())为像素的漂移向量。其中，()和()分别代表在竖直方向和水平方向上的漂移向量。显然，()和()的取值只能是整数。为避免像素漂移之后出现不连续的情况，相邻像素之间的漂移向量应尽量保持一致。定义图像1和2的对齐模型或者对齐能量为

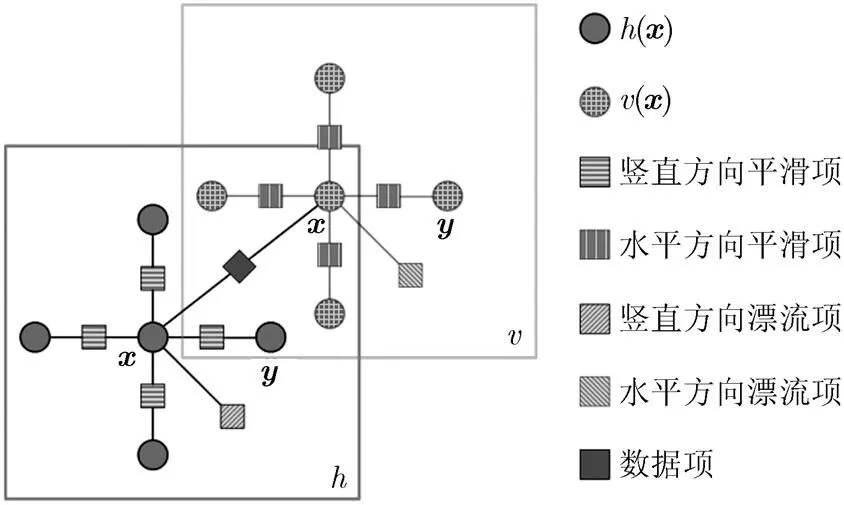
图1 双层信念传播子图示意图

2.3 由粗到精的对齐机制

采用双层环形信念传播算法的问题在于整个算法的复杂度随着图像分辨率的增大而急剧增加。例如，优化一幅100×100和一幅80×80大小的图像之间的对齐模型耗时约50 s，而优化两幅256×256大小的图像则需要2 h，仅存储式(1)中数据对齐项中的数据就需要大约16 G的内存。为此，本文设计一种由粗到精的对齐机制来加快DSFA的优化速度。该机制的基本思想是在粗的尺度上大致估计漂移量，然后逐渐传播并细化到精细的尺度。整个优化过程如图2所示。建立3层不同尺度的图像金字塔{s},=1, 2, 3。其中1的分辨率与原始图像大小一样，而图像s+1通过图像s下采样得到。假设k表示在第个尺度需要被对齐的像素坐标，表示像素在第个尺度上的最优漂移向量，k表示搜索最优漂移向量的窗口中心坐标。在图像金字塔最高层3中，搜索窗口的中心设置为3=3。为确保全搜索，搜索窗口的大小设置为，其中为3的宽度或者高度。所以3层信念传播算法的复杂度为。当信念传播算法收敛以后，整个系统将像素3的最优漂移向量传播给下一层。信念传播算法将在以为中心，大小为的搜索窗口中搜索最优的漂移向量。整个优化过程重复迭代直到计算得到。这种由粗到精的算法复杂度为，大大优于原始的优化算法复杂度。实际应用中，使用双核2.7 GHz因特尔CPU和32 G内存的PC机，采用由粗到精的对齐机制来优化两幅256×256大小的人脸图像仅仅只需要大约30 s，比原始优化算法提高了4倍速率。

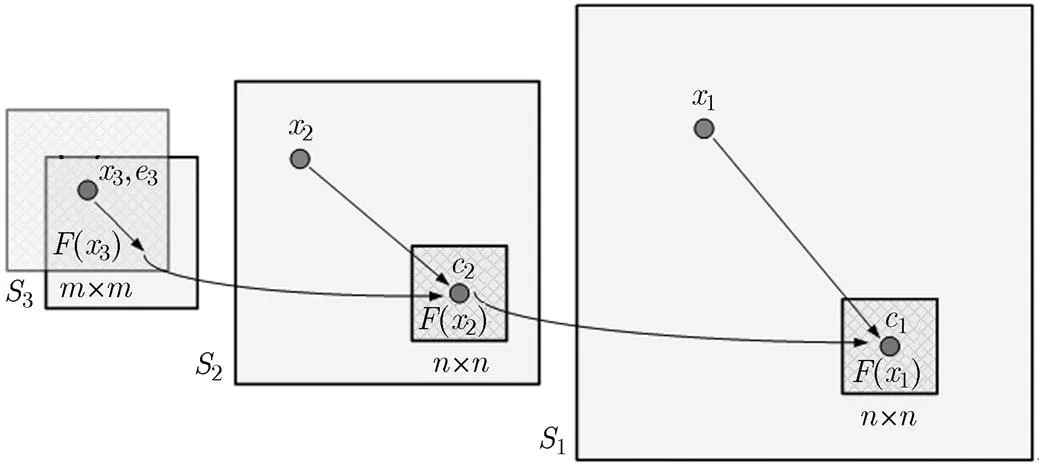
图2 由粗到精的对齐机制示意图(阴影窗口表示在第k个尺度上像素x k的搜索窗口)

图3展示了ORL数据集[8]中3个人脸图像进行对齐的例子。其中最左边是任意选择的测试人脸图像，剩下的人脸图像分别向选择的测试图像对齐。尽管受到不同的旋转、遮挡以及姿态和表情变化的影响，采用DSFA的方法可以很好地将同一类别的训练图像向测试图像进行对齐。图3的最右边还展示了不同类别的训练图像向测试人脸图像对齐的效果，可以看出不同类别的训练图像在经过DSFA 后与测试图像依然存在很大的形变。

图3 ORL数据集中运用DSFA算法进行对齐的3个例子

3 基于DSFA的人脸识别

传统SRM将测试样本通过训练样本集合张成的空间线性近似表达[16]，并通过优化模型中系数向量的稀疏性来求解人脸识别问题。如图3所示，经过DSFA算法进行人脸对齐之后，同一类别的训练图像可以向测试图像进行对齐，而不同类别的训练图像不能很好的与测试图像对齐。这意味着如果利用传统的SRM来建模对齐后人脸图像的识别问题，并不影响系数向量的稀疏性。本节结合DSFA对齐算法，提出一种改进的SRM模型及其对应的人脸识别算法。

3.1改进的SRM模型

3.2 基于SRM模型的人脸识别算法

整个识别过程如表1所示。本文采用对偶的线性规划算法[22]来实现范数的最小化优化计算。

表1 SRM模型分类算法

4 仿真实验以及实验结果

4.1 数据集

ORL人脸数据集[8]包含40个人的400幅灰度图像。这些图像包含不同表情的正脸图像和非正脸图像，如睁眼和闭眼，张嘴和微笑等；不同的遮挡，如佩戴眼镜；以及姿态和旋转等。本文采用ORL数据集的另外一个主要原因在于这些人脸图像来自于不同的性别和年龄。

AR人脸数据集[23]包含126个人(70个男人和56个女人)的4000幅彩色图像。这些人脸图像都是正脸图像，主要包含不同的人脸表情变化(如微笑，发怒，哭喊以及无变化等)；光照变化；以及遮挡变化(太阳镜以及围巾)。采用这个数据集用来测试本文方法在表情变化下的鲁棒性。

LFW人脸数据集[24]一共包含5749个人的13233幅彩色图像。这些人脸图像都具有较大的姿态、旋转以及表情变化。本文首先采用人脸检测算法[25]在原始图像中检测人脸区域，然后在原始图像中截取分辨率为大小的人脸图像。采用这个数据集的目的在于测试本文方法在旋转、姿态以及表情等非刚性变化对人脸识别的影响。

4.2 实验环境设置

本文选择6种人脸识别算法，从识别精度和执行效率两个方面做性能比较。这些方法分别是：TPFRS算法[18]，LBP算法[9]，PCA算法[14]， ICA算法[15]，GNN算法[2]以及FF算法[12]。3个数据集中每幅图像都下采样到分辨率大小的图像。为避免固定的训练样本对算法性能产生的影响，本文在LFW数据集上做10次交叉验证[24]，在另外两个数据集上做30次交叉验证，其中，50%的样本用于训练，10%的样本用来做交叉验证，40%的样本用于测试。实验中参数设置为0.7。式(1)中其他所有参数设置准则为：极端误匹配的情况下(如白色像素匹配到黑色像素或者黑色像素匹配到白色像素)，可能的最大取值为(RGB 3个通道)。是一个经验参数。在固定其他参数的前提下，当=1.275时在验证集上获得最优识别性能。此外，本文要求像素的漂移向量与毗邻的4个像素的漂移向量尽量保持一致，因此对取值较大，为=500。门限的作用和类似，其取值与有关。由于所有图像下采样到分辨率大小，那么水平方向或者竖直方向匹配的极端情况是，因此，本文中的取值为。

4.3实验结果

表2展示了本文算法在3个数据集上的平均识别精度以及执行效率，并与其他基准算法做了性能对比。为检测交叉验证对算法性能的影响，每种方法在第2行还分别展示了识别精度和执行效率的方差。从表2可以看出，本文算法在3个数据集上都取得了最好的识别精度。与LFW数据集相比，ORL和AR数据集包含较少的人脸图像，并且人脸图像的变化简单。因此，本文方法在ORL和AR数据集上取得较高的识别精度(100%, 99.3%)，而在LFW数据集上识别精度相对较低(95.7%)。此外，与采用传统稀疏表达模型的TPFRS方法[18]相比，本文方法在ORL, AR和LFW 3个数据集上的识别精度分别提高了1.4%, 2.1%和9.4%，平均提高了4.3%。可以看出，本文方法在LFW数据集上能取得较高识别精度的增益，这是因为LFW数据集中大部分人脸图像都受到非刚性形变的影响，而本文提出的DSFA方法很好地解决了这类人脸图像的对齐问题。执行效率方面，本文方法在3个数据集上识别一幅人脸图像的平均时间分别为0.45 s, 0.43 s和0.40s，而TPFRS算法[18]的识别时间分别为2.48 s, 2.87 s和2.32 s，大约提高了6倍的识别效率。基于重建的人脸识别方法(如PCA和ICA模型)对非刚性变化非常敏感，而本文采用DSFA的对齐机制对旋转、表情以及姿态变化具有鲁棒性。虽然TPFRS算法在ORL数据集[8]和AR数据集[23]上也取得了较好的性能，但是很难解决非刚性变换后人脸图像的识别问题。尤其在LFW这种存在剧烈非刚性变换的数据集上，性能下降很快，而本文算法依然可以获得95.7%的识别精度。在所有基准算法中，TPFRS[18]算法性能最好，但是计算效率较低。FF算法[12]，GNN算法[2]和LBP算法[9]性能相当，而PCA算法[14]和ICA算法[15]性能最差。

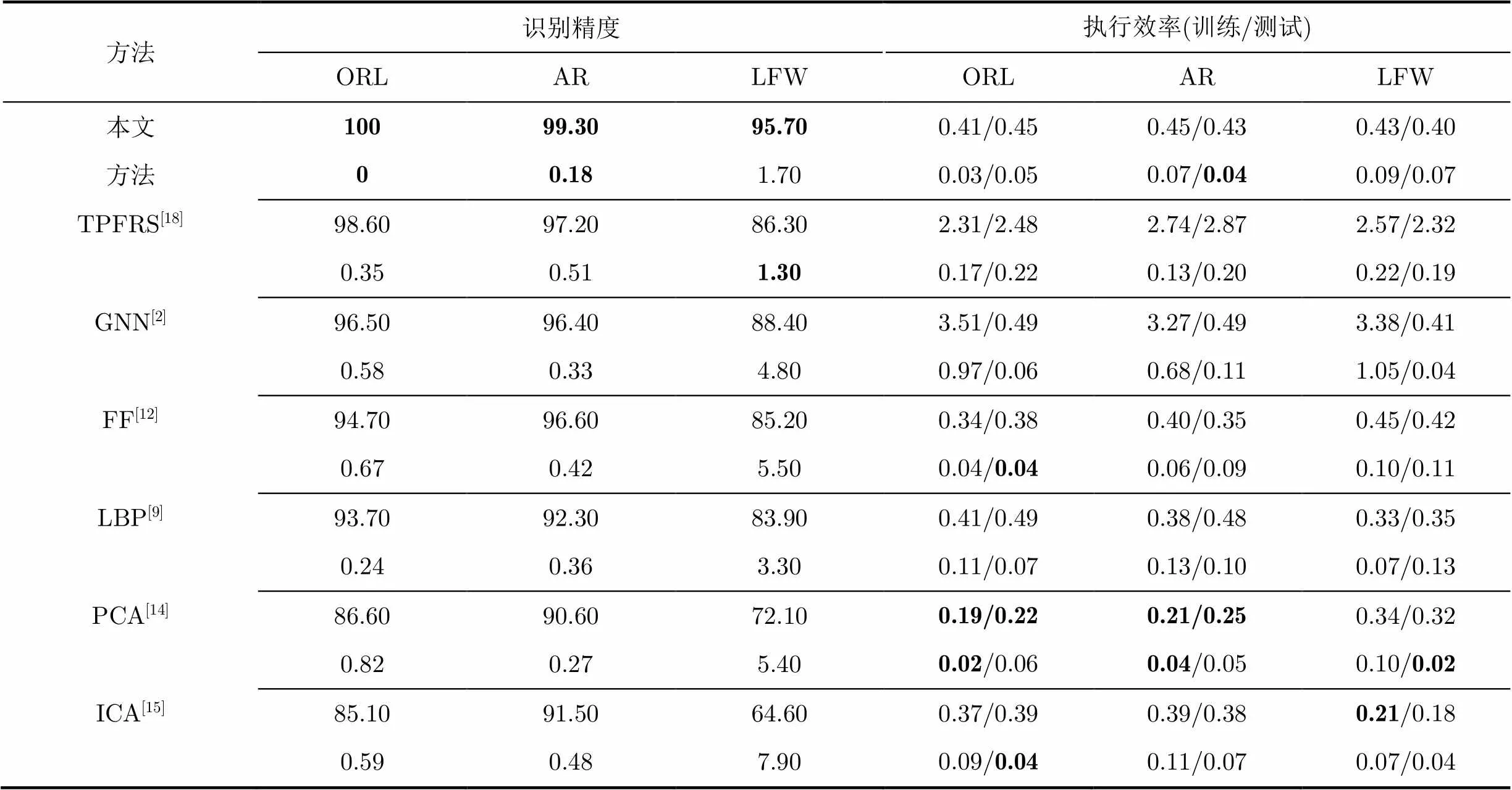
表2不同方法在ORL数据集[8]、AR数据集[23]和LFW数据集[24]上的性能对比

4.4 训练样本个数对识别精度的影响

本文还测试了训练样本个数对整体性能的影响。图4展示了本文算法在ORL数据集[8]和AR数据集[23]上随着训练样本个数变化而导致识别精度的变化。本文选择TPFRS算法[18]，GNN算法[2]以及FF算法[12]作为基准对比算法。可以看出，随着训练样本的增加，所有方法的性能都得到提升。相比之下，本文获得了最好的识别精度。在ORL数据集[8]上，本文算法在50%训练样本的情况下还取得了100%识别精度。

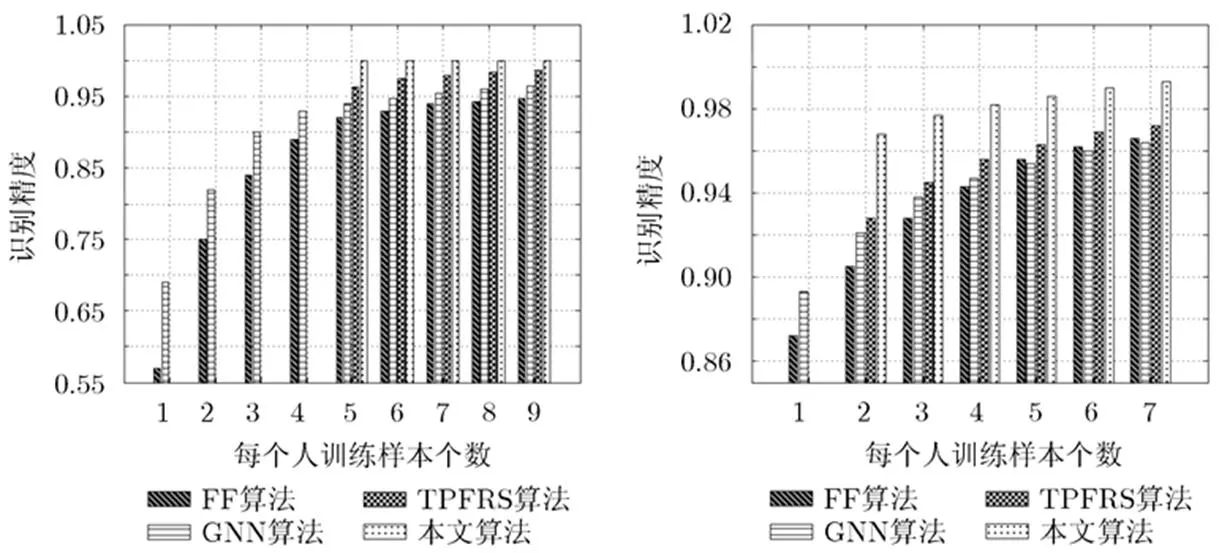
图4 在ORL数据集和AR数据集上识别精度随着训练样本个数的变化

4.5 运行效率对比

表1中还展示了本文算法和其他算法的执行效率，并对比了训练和识别所需要的平均时间和方差。所有算法结果在双核2.7GHz因特尔CPU和32G内存的PC机上运行得到。可以看出，本文算法的平均识别效率要快于TPFRS算法[18]，GNN算法[2]和LBP算法[9]，但是要慢于FF算法[12]，PCA算法[14]以及ICA算法[15]。具体而言，运用DSFA 算法进行图像对齐大致需要0.28 s，而识别过程需要耗时0.15 s。

4.6由粗到精对齐机制的收敛性

在使用DSFA算法进行人脸对齐的过程中，一个自然的问题在于使用由粗到精的对齐机制与不采用由粗到精的对齐机制相比，是否能收敛到相同的最小的能量。为此，本文随机抽取200对人脸图像进行实验。所有图像分辨率首先归一化到大小，然后运用DSFA算法进行人脸对齐。图5展示了使用由粗到精和不使用由粗到精两种机制下式(1)的最小能量。其中横轴是采用由粗到精对齐机制下的最小能量，纵轴是不采用由粗到精对齐机制下的最小能量。采用由粗到精的对齐机制平均耗时31 s，而不采用由粗到精的对齐机制则要耗时127 min。如图5所示，不使用由粗到精对齐机制能够获得更小的对齐能量，而且大多数情况下，采用由粗到精对齐机制下的对齐能量都能收敛到不采用由粗到精对齐机制下的对齐能量。

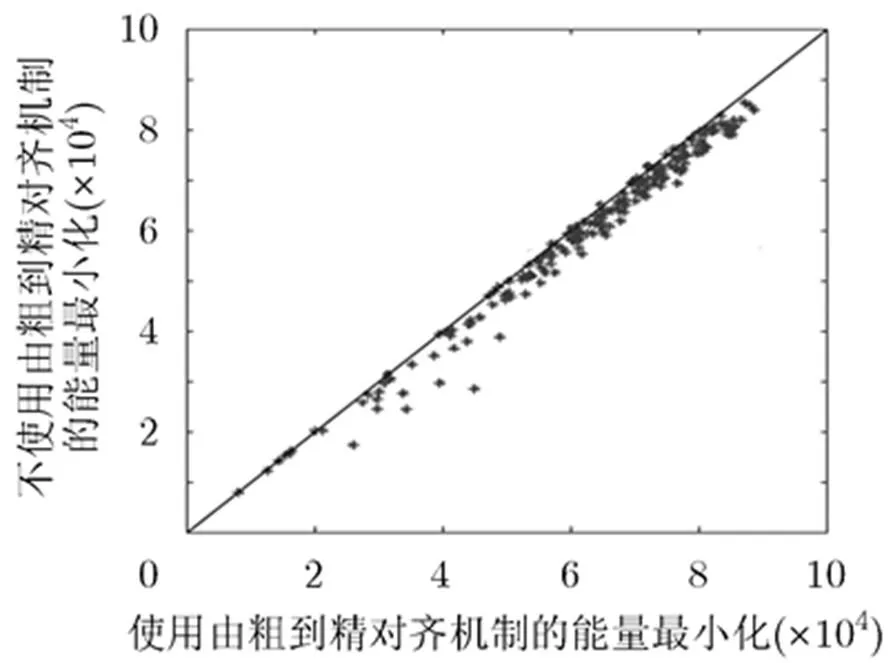
图5 采用由粗到精对齐机制下对齐能量的收敛性

5 结束语

本文提出了一种有效克服非刚性视觉变换的人脸识别方法。采用DSFA算法能够将同一类别的训练样本大致对齐到测试样本，而不同类别的训练样本不能对齐到测试样本；然后提出一种改进的SRM 模型，并利用模型中系数向量的稀疏性来识别不同类别的人脸图像。实验结果表明本文方法在ORL，AR以及LFW数据集上的识别精度和执行效率要优于其他人脸识别模型。后续工作将探讨如何运用本文方法解决视频序列中人脸图像的识别问题。

参考文献

[1] Li S Z and Jain A K. Handbook of face recognition[M]. New York, Springer, 2011: 1-374.

[2] Yang A Y, Zihan Z, Ganesh B A,.. Fast-minimization algorithms for robust face recognition[J]., 2013, 22(8): 3234-3236.

[3] Cament A L, Castillo L E, Perez J P,.. Fusion of local normalization and Gabor entropy weighted features for face identification[J]., 2014, 47(2): 568-577.

[4] Jonathon P P and Alice O J. Comparison of human and computer performance across face recognition experiments[J]., 2014, 32(1): 74-85.

[5] Radtke V W P, Granger E, Sabourin R,.. Skew-sensitive boolean combination for adaptive ensembles-An application to face recognition in video surveillance[J]., 2014, 20(10): 31-48.

[6] Abdullah M F A, Sayeed S M, Sonai K M,.. Face recognition with symmetric local graph Structure[J]., 2014, 41(14): 6131-6137.

[7] 殷飞, 焦李成, 杨淑媛. 基于子空间类标传播和正则判别分析的单标记图像人脸识别[J]. 电子与信息学报, 2014, 36(3): 610-616.

Yin Fei, Jiao Li-cheng, and Yang Shu-yuan. Subspace label propagation and regularized discriminate analysis based single labeled image person face recognition[J].&, 2014, 36(3): 610-616.

[8] 赵振华郝晓弘.局部保持鉴别投影及其在人脸识别中的应用[J]. 电子与信息学报, 2013, 35(2): 463-467.

Zhao Zhen-hua and Hao Xiao-hong. Linear locality preserving and discriminating projection for face recognition [J].&, 2013, 35(2): 463-467.

[9] Ahonen T, Hadid A, and Pietikainen M. Face description with local binary patterns: Application to face recognition[J]., 2006, 28(12): 2037-2041

[10] 张洁玉, 赵鸿萍, 陈曙. 自适应阈值及加权局部二值模式的人脸识别[J]. 电子与信息学报, 2014, 36(6): 1327-1333.

Zhang Jie-yu, Zhao Hong-ping, and Chen Shu. Face recognition based on weighted local binary pattern with adaptive threshold[J].&, 2014, 36(6): 1327-1333.

[11] Cootes T F, Edwards G J, and Taylor C J. Active appearance models[J]., 2001, 23(6): 681-685.

[12] Belhumeur P N, Hespanha J P, and Kriegman D J. Eigenfaces vs. fisherfaces: recognition using class specific linear projection[J]., 1997, 19(7): 711-720

[13] Naseem I, Togneri R, and Bennamoun M. Linear regression for face recognition[J]., 2010, 32(11): 2106-2112

[14] Turk M and Pentland A. Eigenfaces for recognition[J]., 2010, 3(1): 71-86.

[15] Bartlett M S, Movellan J R, and Sejnowski T J. Face recognition by independent component analysis[J]., 2002, 13(6): 1450-1464.

[16] Wright J, Yang A Y, Ganesh A,.. Robust face recognition via sparse representation[J]., 2009, 31(2): 210-227

[17] Peng Y, Ganesh A, Wright J,.. Rasl: Robust alignment by sparse and low-rank decomposition for linearly correlated images[J]., 2012, 34(11): 22330-2246.

[18] Wagner A, Wright J, Ganesh A,.. Toward a practical face recognition system: Robust alignment and illumination by sparse representation[J]., 2012, 34(2): 372-386.

[19] Lowe D G. Distinctive image features from scale-invariant keypoints[J]., 2004, 60(2): 91-110.

[20] Shekhovtsov A, Kovtun I, and Hlavac V. Efficient MRF Deformation Model for Non-Rigid Image Matching[C]. Proceedings of the IEEE Computer Vision and Pattern Recognition, Miami, FL, USA, 2007: 1-6.

[21] Felzenszwalb P F and Huttenlocher D P. Efficient belief propagation for early vision[J]., 2006, 70(1): 41-54.

[22] Boyd S and Vandenberghe L. Convex Optimization[M]. London, Cambridge University Press, 2004: 457-514.

[23] Martinez A M. The AR face database[R]. CVC Tech. Rep. 1998.

[24] Huang G B, Ramesh M, Berg T,.. Labeled faces in the wild: A database for studying face recognition in unconstrained environments[R]. University of Massachusetts, Amherst Tech. Rep. 7-49, 2007.

[25] Viola P and Jones M J. Robust Real-Time Face Detection[J], 2004, 57(3): 137-154.

Improved Sparse Representation Algorithm for Face Recognition Via Dense SIFT Feature Alignment

Zhou Quan Wei Xin Chen Jian-xin Zheng Bao-yu

(,,210003,)

In order to address the non-rigid deformation (e.g., misalignment, poses, and expression) of facial images, this paper proposes a novel sparse representation face recognition algorithm using Dense Scale Invariant Feature Transform (SIFT) Feature Alignment (DSFA). The whole method consists of two steps: first, DSFA is employed as a generic transformation to roughly align training and testing samples; and then, input facial images are identified based on proposed sparse representation model. A novel coarse-to-fine scheme is designed to accelerate facial image alignment. The experimental results demonstrate the superiority of the proposed method over other methods on ORL, AR, and LFW datasets. The proposed approach improves 4.3% in terms of recognition accuracy and runs nearly 6 times faster than previous sparse approximation methods on three datasets.

Face recognition; Face alignment; Dense Scale Invariant Feature Fransform (SIFT) Feature; Sparse representation model

TP391.41

A

1009-5896(2015)08-1913-07

10.11999/JEIT141194

周全 quan.zhou@njupt.edu.cn

2014-09-12收到，2015-04-24改回，2015-06-08网络优先出版

国家自然科学基金(61201165, 61271240, 61401228, 61403350)和南京邮电大学科研基金(NY213067)资助课题

周 全： 男，1980年生，讲师，研究方向为计算机视觉、模式识别.

魏 昕： 男，1983年生，副教授，研究方向为模式识别.

陈建新： 男，1971年生，副教授，研究方向为多媒体信号处理.

郑宝玉： 男，1945年生，教授，研究方向为多媒体信号处理、多媒体通信.