基于角点保护的偏微分方程图像插值方法
肖志涛 冯铁君 张 芳 耿 磊 吴 骏 李月龙 王丹钰 陈 颖
基于角点保护的偏微分方程图像插值方法
肖志涛①冯铁君①张 芳*①耿 磊①吴 骏①李月龙②王丹钰①陈 颖①
①(天津工业大学电子与信息工程学院 天津 300387)②(天津工业大学计算机科学与软件学院 天津 300387)
图像插值是数字图像处理领域中的一个基本问题,利用插值技术可以实现图像的缩放和图像恢复。传统的插值方法易使边缘产生锯齿效应或使插值结果模糊不清。该文提出一种基于角点保护的偏微分方程插值方法。该方法针对图像中不同的特征进行特定插值,在保持边缘结构清晰的同时,还能保护尖锐的角形结构,有效改善插值后图像的整体视觉效果和峰值信噪比。此外,对方程的主要参数进行分析,提出了相应的参数确定方法,从而提高该方法的适用性。
图像插值;图像放大;偏微分方程;角点;边缘
1 引言
图像插值是数字图像处理中的基本问题之一,常用于图像放大,是由一个低物理分辨率(Low Physical Resolution, LPR)的模糊图像插值重建对应高物理分辨率(High Physical Resolution, HPR) 的清晰图像,在医学图像分析、航空航天、广告宣传等许多领域有重要作用[1]。传统的插值方法,包括最近邻插值、双线性插值等操作简单,速度快,但会使图像的处理结果产生锯齿状边缘。高分辨率插值方法包括双三次插值、三次B样条插值以及Newton Thiele插值[2]等,虽然可以平滑边缘锯齿,但都需要使用一些已知的光滑函数或函数结构,这些固定函数的局限性势必会影响图像质量,而且放大倍数越大,图像质量受此影响越多。
为了克服这些不足之处,引入了基于偏微分方程[3](Partial Differential Equation, PDE)的图像插值方法。文献[4]提出了经典的各向异性扩散PM模型,其扩散函数是随图像局部性质变化而变化,它能够起到保护图像边缘的作用。文献[5]提出以热传导方程为模型进行插值,该方法运算量小、处理时间短、图像具有较好的平滑性,但迭代次数较多时,图像的边缘信息就会大量丢失,从而造成边缘模糊的现象。文献[6]提出基于边缘增强的方向扩散PDE,利用边缘停止函数抑制边缘法线方向的扩散,达到保护边缘的目的。文献[7]把方向扩散PDE与角点约束算法相结合,抑制方向扩散PDE在角形区域及边缘处的扩散,进而提高图像视觉效果。文献[8]为解决四阶PDE产生的过度平滑问题,提出基于边缘检测的四阶PDE,减少了方程在图像边缘的扩散。应用PDE处理图像涉及到一个非常重要的问题,即方程参数的选择问题。方程的参数包括两种,一是方程的内部参数,如扩散系数和保真系数等。另一种是对方程进行离散求解时用到的参数,参数的选取是否恰当与PDE模型的插值效果直接相关,甚至影响方程的稳定性。
本文引进角点保护算子与边缘冲激滤波器结合,根据图像的不同特征在相应位置采用不同的插值策略,从而更好地保护图像边缘和角点。本文主要有两个目的。第一,为了实现对角点结构的自适应保护,在方程中引入角点保护算子作为扩散系数;第二,分析并得出离散求解偏微分方程的最优参数,包括保真项系数、扩散项系数、时间步长和迭代次数。
2 基于角点检测算子约束的PDE图像插值算法
2.1图像插值的退化建模
退化建模是图像插值中的首要问题,即建立高分辨率图像(HPR)和低分辨率图像(LPR)之间的关系。假设HPR与LPR图像的采样因子之比为,可建立式(1)退化模型。
2.2 图像的角点求取
角点是图像的重要特征,在图像匹配、目标跟踪、图像建模等领域具有重要的应用。为了保证图像处理结果的视觉效果和图像质量,保持图像细节,必须在插值放大过程中保护角点。
在本文中,利用散布矩阵(scatter matrix)求取角点,其公式定义为

考虑局部邻域可以识别角形结构,角点计算公式为
由于散布矩阵是根据图像的局部邻域结构特征识别和确定角形结构,因此基于散布矩阵求取的角点比基于差分算子求取的角点更稳定,抗噪性更好[9]。
2.3基于角点检测算子约束的PDE图像插值算法
PDE图像处理方法[10]把图像处理变换看做PDE的算子,利用PDE将初始图像变形,通过求解偏微分方程完成图像插值放大。
基于PDE的图像插值算法主要以边缘增强的方向扩散偏微分方程为代表[6]:
上述边缘增强的偏微分方程图像插值算法虽然可以充分保护图像边缘,但方程中没有针对角形结构进行相应保护,导致插值结果图像中角形结构钝化,使原本尖锐的特征角点变为平滑的圆形结构。文献[7]提出了一种角点检测算子约束的偏微分方程图像插值算法,其基本思想是在每个角点对应的角形区域建立半径为的圆形(记为屏障指示函数:
3 基于角点保护算子的PDE图像插值算法
由2.3节可知,角点检测算子约束的PDE图像插值算法虽然能够保护角点,但是屏障指示函数内部扩散被完全禁止,导致过分保护角点,使角点处与边缘衔接不自然,影响图像质量。为了在保护角点结构同时不影响图像的视觉效果,本文根据边缘停止函数[4],推导出角点保护算子,表示图像的角点。这样,基于角点保护算子的PDE图像插值算法可以表述为
4 PDE参数分析
4.1 偏微分方程的离散差分形式
由于图像是以像素为单位存储在计算机中的,所以在用PDE对图像进行处理时,首先要对其进行离散化[12]。假设离散差分步长为,在方程的演化过程中,时刻的演化图像可以表示为。点处,时刻的时间差分可以用一个前向差分来计算,即
采用的空间差分为
求解插值图像过程中,需要用到两类参数。一类是方程的内部参数,包括边缘冲激函数系数,保真项系数、边缘停止函数和角点保护算子中的,一般取经验值0.025[6];另一类是方程的离散求解参数,包括扩散系数和最优停止时间(即迭代次数)。这些参数的取值对插值结果有重要影响,下面通过实验分析得出,,的最优值,并实现的自适应选取。

图1 变化曲线
4.3保真项系数
4.4 离散差分步长
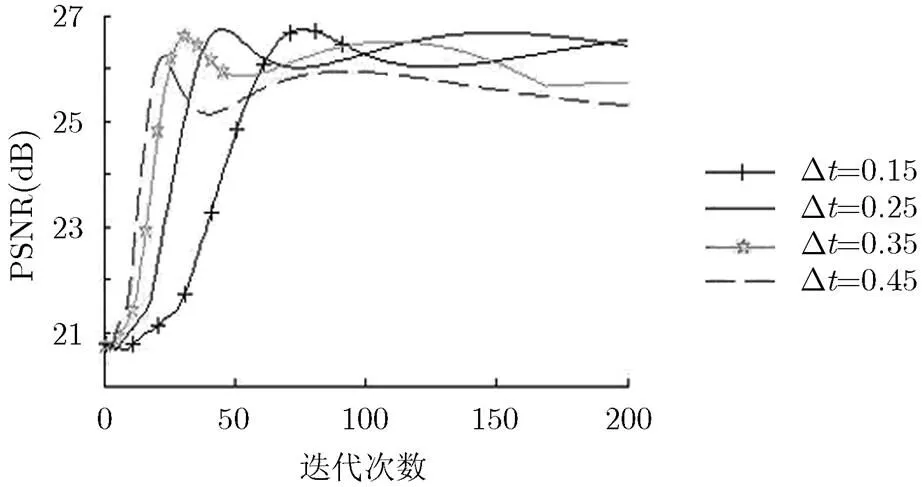
图2 每个迭代200次对应PSNR曲线
图3(a1)~图3(a4)给出了4幅测试图像,图3(b1) ~图3(b4)为4幅测试图像在循环过程中得到的最大PSNR的变化曲线,从实验结果可以看出,当= 0.25时PSNR达到最大值,或小于0.25时PSNR最大值的变化趋于平缓。因此本文取0.25。

图3 插值图像在不同差分步长取值下的最大PSNR变化曲线及不同迭代次数下的清晰度曲线
4.5迭代次数
对像素复制图像进行插值时,清晰度先增后减,清晰度随迭代次数的变化曲线如图3(c1)~图3(c4)所示。初始像素复制图像边缘很模糊,清晰度低;随着插值的进行边缘细节逐渐加强,清晰度上升至最大值;若迭代次数继续增大,清晰度反而会下降,这是因为迭代次数过多时,会导致方程对像素间的灰度融合作用大于灰度插补作用。因此,应选择清晰度最高点对应的迭代次数。本文利用清晰度比值(Resolution Ratio) RR选择迭代次数,设R和R分别对应迭代结果和初始图像(即LPR图像的像素复制图像)的清晰度,定义。设定迭代时间间隔为4.4节中得到的经验数值,。为了得到该最高点,同时避免迭代过程中有可能出现的小幅度波动的干扰,当满足式(19)时,对应的迭代次数即为最优迭代次数。同样对图3(a1)~ 图3(a4)中的4幅图像进行测试,最优迭代次数分别为1=64,2=143,3=116,4=66。
5 实验与结果分析
利用本文方法对图像进行插值放大。为了说明本文方法的优势,与几种典型的PDE插值方法进行对比。采用插值图像的PSNR和图像熵值,同时结合主观视觉效果(包括边缘清晰度及锯齿效应、角形尖锐度、边缘附近和平坦区域中的振铃效应)对插值算法进行客观和主观综合评价[14,15]。
实验1 运用本文提出的基于角点保护算子的PDE,以图3(a1)为例结合给出的参数确定方法对LPR图像的像素复制图像进行插值处理,并与四阶PDE[16]、方向扩散PDE、角点检测算子约束的PDE进行比较。原始HPR图像如图4(a)所示,大小为256×256像素,根据退化模型式(2)将图4(a)进行4倍率下采样,得到64×64的LPR图像,如图4(b)所示。对LPR图像进行像素复制,得到256×256大小的灰度图像,如图4(c)所示,作为插值初始图像,分别利用上述4种方法对图4(c)进行插值处理。在本实验中,取,用4.3节算法计算。图4(d)~图4(g)分别展示了上述4种方法插值结果的局部放大图像(选取图4(c)中白色框内的部分),可以明显看出图4(d)效果明显模糊;图4(e)效果虽然边缘清晰但是角点钝化,细节丢失;图4(f)效果明显优于前两种方法,但是由于其方法在插值过程中角点处的扩散被完全禁止,导致角点突兀,图像整体效果不自然;图4(g)效果图特征更为清晰,边缘角点过渡自然,提高了整体视觉效果。为了证明本文自适应算法的普适性,对图3(a1)~图3(a4)组中的所有图像用4种插值方法进行插值,并对结果进行定量评价,如表1所示。可以看出,本文方法得到的插值结果PSNR值最大,而四阶PDE的插值结果PSNR值最小,这是因为四阶PDE不能有效保护边缘信息,造成了图像模糊;此外本文方法插值图像的信息熵仅次于四阶PDE,后者在边缘模糊的情况下仍能获得最高的信息熵,说明它在本应平坦的区域内部引入了噪声。综合两个评价指标,本文插值结果在信噪比最大的基础上图像信息量高,说明本文方法在保持图像细节,包括边缘和角型结构时更具优势。

图4 4种方法插值结果比较

表1各方法PSNR及H数值比较
实验2 运用本文提出的基于角点保护算子的PDE对LPR图像直接进行插值放大。在该组实验中LPR图像如图5(a)所示,分别用上述4种方法进行直接插值放大。直接插值放大时,极易产生边缘锯齿效应,因此在处理时应加强切线方向滤波强度以平滑锯齿,所以本实验中取,其他参数为,用4.3节给出的算法计算。4种方法的处理结果如图5所示。用清晰度对插值结果进行客观评价,4种方法的清晰度分别为32.37, 35.56, 33.73, 36.66。本文方法得到的结果清晰度最高,说明该方法可以有效保护图像中的边缘和角点结构。

图5 4种方法直接插值放大效果图
实验3 去除图像边缘的锯齿。在此项实验中,原始图像的锯齿非常明显,由于待处理图像与期望的处理结果出入较大,为了有效去除锯齿,需要减少保真项的比重,并加强切线方向的平滑强度。因此本实验中取保真项系数。本文给出了两组实验结果,如图6所示。最优迭代次数分别为和,其他参数同取。对于两组结果,方向PDE插值方法所得到的结果图清晰度分别为28.99和29.25,而利用本文方法插值的结果图清晰度为32.89和39.54,表明本文方法得到的插值结果更加清晰。从图6中也可明显看出,两种方法都能有效去除边缘锯齿,但相比于方向扩散PDE插值方法而言,本文方法在保持图像角点结构的尖锐性方面效果更佳。

图6去除锯齿效果图
实验4 对含噪图像进行插值处理。由于PDE插值方案中融入了灰度值扩散的思想,因此在插值的同时具有一定的滤波去噪功能[17]。图7(a)对图4(c)加入了方差为15的高斯噪声,分别用方向扩散PDE、角点检测约束PDE和本文算法进行插值,结果如图7所示。由于噪声图像局部梯度较高,为了有效滤除噪声,需要加强滤波强度,因此本实验中取,其他参数取,用4.3节算法计算。图7(b)图7(d)分别是3种方法插值结果的局部放大图像(选取图7(a)中白色框内的部分),可明显看出图7(b)边缘严重模糊;图7(c)虽然清晰但是角点处过于突兀;图7(d)整体效果清晰,且边缘角点过渡自然。经计算3种方法插值结果的PSNR值分别是75.14, 77.10, 77.78,本文方法优于前两种方法。

图7 对含噪图像的插值效果图
6 结论
本文针对图像边缘和角点在插值放大后出现模糊造成细节丢失等问题,提出了基于角点保护算子的PDE图像插值方法,有效控制不同特征像素点的扩散速度,在图像的平滑区域得到充分插值的同时,有效保护图像边缘和角点等重要信息。此方法不仅可以消除边缘锯齿效应,也可以抑制角形区域的扩散,并用实验证明了此方法的可行性和优势。在此基础上,本文还分析了各参数的取值范围,解决了尝试性选取参数的盲目性。将本文方法应用于图像插值放大中,定性和定量分析均表明了本文方法的有效性。
参考文献
[1] Jha A, Kumar A, Schaefer G,.. An efficient edge preserving image interpolation algorithm[C]. 3rd International Conference on Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 2014, DOI:10.1109/ ICIEV.2014.6850820.
[2] Yang Z, Lu F, and Guan L. Image enlargement and reduction with arbitrary accuracy through scaling relation of B-spline[J]., 2001, 13(9): 824-827.
[3] Sarti A, Mikula K, Sgallari F,. Evolutionary partial differential equations for biomedical image processing[J]., 2002, 35: 77-91.
[4] Perona P and Malik J. Scale-space and edge detection using anisotropic diffusion[J]., 1990, 12(7): 629-639.
[5] 朱宁, 吴静, 王忠谦. 图像放大的偏微分方程方法[J]. 计算机辅助设计与图形学学报, 2005, 39(3): 124-132.
Zhu Ning, Wu Jing, and Wang Zhong-qian. Image zooming based on partial differential equations[J].-, 2005, 39(3): 124-132.
[6] Aly H and Dubois E. Image up-sampling using total-variation regularization with a new observation model[J]., 2005, 14(10): 1647-1659.
[7] 邵文泽. 基于图像建模理论的多幅图像正则化超分辨率重建算法研究[D]. [博士论文], 南京理工大学, 2008.
Shao Wen-ze. Image modeling based regularized multi-frame super-resolution reconstruction[D]. [Ph.D. dissertation], Nanjing University of Science and Technology, 2008.
[8] 张帆. 基于偏微分方程与边缘检测的图像去噪算法[J]. 计算机工程与设计, 2014, 35(2): 562-566.
Zhang Fan. Partial differential equation and edge detection based image denoising algorithm[J]., 2014, 35(2): 562-566.
[9] Shao W and Wei Z. Edge-and-corner preserving regularization for image interpolation and reconstruction[J]., 2008, 26(12): 1591-1606.
[10] 季成涛, 何小海, 符耀庆, 等. 一种基于正则化的边缘定向插值算法[J]. 电子与信息学报, 2014, 36(2): 293-297.
Ji Cheng-tao, He Xiao-hai, Fu Yao-qing,An edge directed interpolation algorithm based on regularization[J].&, 2014, 36(2): 293-297.
[11] Bini A and Bhat M. Selective image smoothing and feature enhancement using modified shock filters[C]. 8th Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI) Association of Thailand-Conference, Khon Kaen, 2011: 991-994.
[12] Zhang F, Liu W, Tang C,.. Variational denoising method for electronic speckle pattern interferometry[J]., 2008, 6(1): 38-40.
[13] 郭茂银. 基于四阶偏微分方程的并行图像去噪研究[D]. [硕士论文], 重庆邮电大学, 2011.
Guo Mao-yin. The parallel image denoising research based on fourth-order PDE[D]. [Master dissertation], Chongqing University of Posts and Telecommunications, 2011.
[14] 李朝锋, 唐国凤, 吴小俊, 等. 学习相位一致特征的无参考图像质量评价[J]. 电子与信息学报, 2013, 35(2): 484-488.
Li Chao-feng, Tang Guo-feng, Wu Xiao-jun,. No-reference image quality assessment with learning phase congruency feature[J].&,2013, 35(2): 484-488.
[15] 姜求平, 邵枫, 蒋刚毅, 等. 基于视觉重要区域的立体图像视觉舒适度客观评价方法[J]. 电子与信息学报, 2014, 36(4): 875-881.
Jiang Qiu-ping, Shao Feng, Jiang Gang-yi,An objective stereoscopic image visual comfort assessment metric based on visual important regions[J].&,2014, 36(4): 875-881.
[16] Gao R, Song J, and Tai X. Image zooming algorithm based on partial differential equations technique[J]., 2009, 6(2): 284-292.
[17] Ye Z, Li X, and Li Y. Visual and artistic images denoising methods based on partial differential equation[J]., 2013, 8(3): 284-290.
Image Interpolation with Corner Preserving Based on Partial Differential Equation
Xiao Zhi-tao①Feng Tie-jun①Zhang Fang①Geng Lei①Wu Jun①Li Yue-long②Wang Dan-yu①Chen Ying①
①(,,300387,)②(,,300387,)
Image interpolation is a basic issue in digital image processing, which can be used to realize image magnification and restoration,.. Traditional interpolation methods are easy to make the edge structures produce staircase artifacts or make the interpolated results blurred. An image interpolation method with corner preserving based on Partial Differential Equation (PDE) is proposed, which provides different interpolation applications for different characteristics of the image. The proposed interpolation scheme is not only able to maintain the edge structure clear, but also able to keep the corner sharp. Then, the overall visual and the Peak Signal to Noise Ratio (PSNR) of the interpolation image can be improved effectively. In addition, this paper puts forward methods for selecting the parameters through analyzing the equation, thus it improves the adaptability of the proposed method.
Image interpolation; Image magnification; Partial Differential Equation (PDE); Corner; Edge
TN911.73
A
1009-5896(2015)08-1892-08
10.11999/JEIT141420
张芳 hhzhangfang@126.com
2014-11-05收到,2015-03-05改回,2015-06-08网络优先出版
肖志涛: 男,1971年生,教授,博士生导师,研究方向为图像处理与模式识别、智能信号处理.
冯铁君: 女,1988年生,硕士生,研究方向为偏微分方程图像处理.
张 芳: 女,1981年生,副教授,硕士生导师,研究方向为光学图像处理与检测技术.
耿 磊: 男,1982年生,副教授,硕士生导师,研究方向为测量检测技术与机器视觉.
吴 骏: 男,1978年生,副教授,硕士生导师,研究方向为智能信号处理.
李月龙: 男,1982年生,讲师,研究方向为图像处理与模式识别.
王丹钰: 女,1989年生,硕士生,研究方向为电子散斑干涉测量技术.
陈 颖: 女,1991年生,硕士生,研究方向为图像处理.

