基于环境动态感知的空时自适应处理

方 明 刘宏伟 戴奉周 王小谟②



基于环境动态感知的空时自适应处理

方 明①刘宏伟①戴奉周*①王小谟①②

①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)②(中国电子科学研究院 北京 100041)

在非均匀环境中，缺乏独立同分布的训练样本会使空时自适应处理(Space-Time Adaptive Processing, STAP)算法性能严重下降。针对这个问题，该文提出一种基于环境动态感知的空时自适应处理方法。该方法首先通过发射一组正交信号感知观测场景获取杂波信息；然后利用杂波信息结合平台参数及系统参数预测未来一段时间内杂波的协方差矩阵；最后将预测的协方差矩阵与样本协方差矩阵进行组合以构造空时滤波器。仿真结果表明，与传统的知识辅助类STAP算法相比，该方法在缺乏准确先验知识的情况下依然可以有效地抑制非均匀环境中的杂波。

机载雷达；杂波抑制；空时自适应处理；感知；正交信号

1 引言

对于架设在移动平台上的机载雷达，来自不同方向的杂波具有不同的多普勒频率，因此其杂波具有空时2维的分布特性[1]。为了抑制回波中的杂波分量，我们需进行空时2维的联合滤波，即空时自适应处理(Space-Time Adaptive Processing, STAP)。空时自适应处理需要通过一定数量的训练样本来估计检测单元的杂噪协方差矩阵。但是在实际应用中，由于环境的非均匀性，如地形地貌的变化，人造建筑物等，产生了非均匀样本，导致自适应滤波器的凹口位置与深度发生偏差，从而影响了机载雷达的杂波抑制性能。

对此，文献[6,7]提出利用机载雷达探测环境的先验知识来改善STAP算法的杂波抑制性能，即知识辅助空时自适应处理(Knowledge-Aided STAP, KA-STAP)。根据先验知识的使用方式，KA-STAP一般可分为两类：(1)间接利用先验知识，例如智能地选择滤波器和训练样本；(2)直接利用先验知识，例如贝叶斯滤波及预白化类STAP。第(1)类方式利用数字地形高程数据、地面覆盖/地面使用数据等先验知识选取与环境相匹配的自适应滤波器以及均匀的训练样本；第(2)类方式需通过先前的观测数据或是其它方式获取当前检测单元的先验协方差矩阵。在先验知识准确的情况下，KA-STAP能够极大地改善雷达在非均匀环境中的杂波抑制性能。但是在实际应用中，由于外界环境的改变，造成了先验知识与实际环境的失配，使用这样的先验知识不仅不会改善STAP的杂波抑制性能，甚至可能会降低其性能[2]。

针对上述问题，本文提出了一种基于环境动态感知的空时自适应处理方法。该方法利用天线阵发射正交信号时具有全向方向图的特点，在检测前发射一组正交信号探测外界环境，并通过环境的观测数据估计场景内杂波的散射特性，存入环境动态数据库，完成环境的实时在线感知；检测时先利用数据库中的杂波信息结合平台参数及系统参数预测未来一段时间内的杂波协方差矩阵；之后预测的杂波协方差矩阵与样本协方差矩阵以一定的方式组合生成空时滤波器，抑制回波中的杂波分量。本文通过仿真实验表明：在先验知识与实际环境失配的情况下，该方法依然可以有效地抑制杂波。

2 杂波信息的获取

检测前，雷达发射探测信号主动感知外界环境获取杂波信息，本文将这一阶段称为感知阶段。天线阵发射正交信号时具有全向的方向图，因此通过发射一组正交信号即可获得整个场景的观测，从而节省大量的时间资源；相较于普通波形，发射正交信号时，系统可以获得更高的参数辨别能力。基于以上两个点，本文将正交信号作为环境的探测信号。

2.1环境回波模型

2.2杂波散射特性估计

假设观测场景内的杂波是非均匀的，并且强杂波具有一定的稀疏性(即杂波RCS只有一部分元素的模值较大，其余元素的模值都相对较小)，则通过观测数据，对具有稀疏特性的杂波RCS进行估计的问题可以描述为

3 杂波协方差矩阵预测及空时自适应处理

雷达完成环境的感知后，发射普通的相控阵信号，探测目标，本文将这一阶段称为探测阶段。探测阶段，天线阵的个阵元发射线性调频信号，其中表示探测阶段每个阵元的发射功率，是归一化复包络。此时相干处理间隔内的脉冲数为，脉冲重复间隔为。

3.1杂波块位置信息更新

平台的运动使杂波块与雷达的相对位置不断地发生变化，因此在利用杂波信息前，应先更新杂波块的位置信息。如图1所示，假设感知阶段雷达位于处，杂波块相对雷达的距离及到达角为与，雷达切换到相控阵模式后，经到达，此时该杂波块相对雷达的距离及到达角变为与。在图1中，由余弦定理及正弦定理分别可得

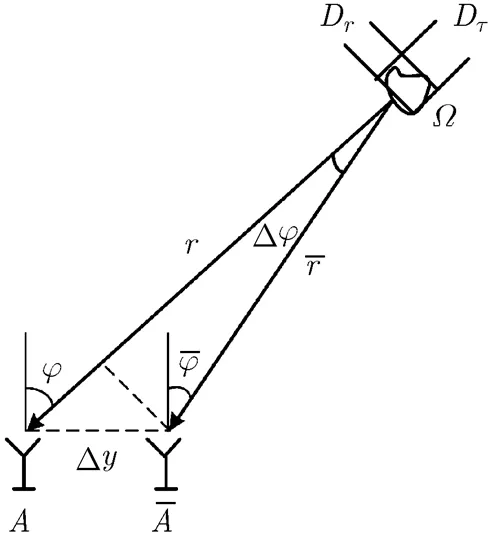
图1 杂波块与雷达的几何关系

3.2杂波协方差矩阵预测

在非均匀的杂波环境中，为了避免非均匀样本数据给杂波协方差矩阵估计带来的影响，本文利用Ward的杂波模型[1]构造检测单元的杂波协方差矩阵。根据Ward的杂波模型，杂波协方差矩阵估计包括杂波强度估计及其导向矢量估计，其中杂波强度取决于杂波的RCS、杂波的距离以及天线的照射功率，导向矢量取决于杂波的到达角，则结构化的杂波协方差矩阵可表示为

3.3空时滤波器设计

考虑到重构场景与实际场景存在一定的误差，且这种误差会影响杂波子空间的估计精度，进而造成杂波抑制性能的下降。因此本文在自适应处理时先利用实际回波数据校正杂波子空间。

根据文献[12]，校正后的协方差矩阵可以表示为

4 杂波信息的时效性分析

如图1所示，对于场景内任一杂波块，雷达平台的运动会使杂波块内部散射点间的相位差发生变化，导致散射点子回波的向量和的幅度发生变化，即杂波块的RCS会随着平台的运动产生一定的起伏。为了保证杂波协方差矩阵估计的精度，需确保雷达在感知阶段与探测阶段对同一杂波块的观测是相关的，但是随着平台的运动，这种相关性逐渐减弱，因此感知阶段获取的杂波信息具有时效性。本节就杂波信息的时效性展开讨论。

4.1稀疏重构的分辨率

在研究杂波信息的时效性前，先讨论稀疏重构算法的分辨率问题。本文参考文献[13]将稀疏重构算法的分辨率定义为：在一定的虚拟孔径()、相干积累脉冲及杂噪比CNR下，以概率成功地将两个杂波块检测出来的最小角度间隔。

由于很难给出上述分辨率的理论值，因此本文通过蒙特卡洛实验的方法得到该理论值的估计。

4.2杂波信息的时效性

平台的运动会导致杂波块RCS的起伏，在这种情况下，杂波块的点目标模型[1]就不够精确。为了更好地描述杂波块RCS随平台运动的起伏特性，这里将杂波块建模为分布式目标。在图1中，假设杂波块由一组分布在中的个散射点组成。则根据文献[14]，当满足式(21)时：

由4.1节定义的分辨率，重构杂波的切向尺寸可表示为

将式(22)和式(23)代入式(21)，得到保持杂波RCS相关的平台位移量

将式(24)右端定义为杂波的相关距离，且规定每当平台位移量超出杂波相关距离后，雷达需重新发射正交信号感知观测场景，更新杂波信息，以保证杂波协方差矩阵估计的精度。

5 仿真实验

本节利用仿真数据来验证本文所提方法的有效性。

实验场景设置：将一幅SAR图像作为实际场景，且每个像素的幅值作为散射点的强度，如图2所示。

图2 某地区的SAR图像

系统参数设置：雷达的系统参数如表1所示，平台参数如表2所示。

表1系统参数

表2平台参数

5.1实验1：重构算法的分辨率及杂波的相关距离

在上述的实验条件下，令环境回波的杂噪比分别为0 dB, 10 dB, 20 dB, 30 dB, 40 dB，对稀疏重构算法进行1000次蒙特卡洛实验，得到检测概率时稀疏重构的分辨率，实验结果如图3所示。从图中可以看出稀疏重构算法较瑞利限具有一定的超分辨能力，且杂噪比越大稀疏重构算法的分辨力也越强，但是随着杂波到达角的增大，分辨力随之下降，尤其是当到达角大于80°后，分辨力急剧下降。

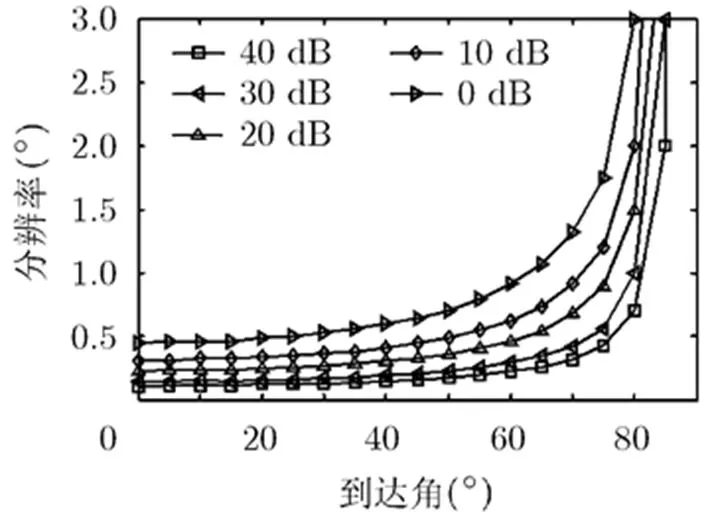
图3 重构算法的分辨率

将重构算法的分辨率代入式(24)，得到杂波的相关距离，如图4所示。从图中可以看出杂噪比越大杂波的相关距离也越大，且当杂波到达角小于时杂波的相关距离基本固定。

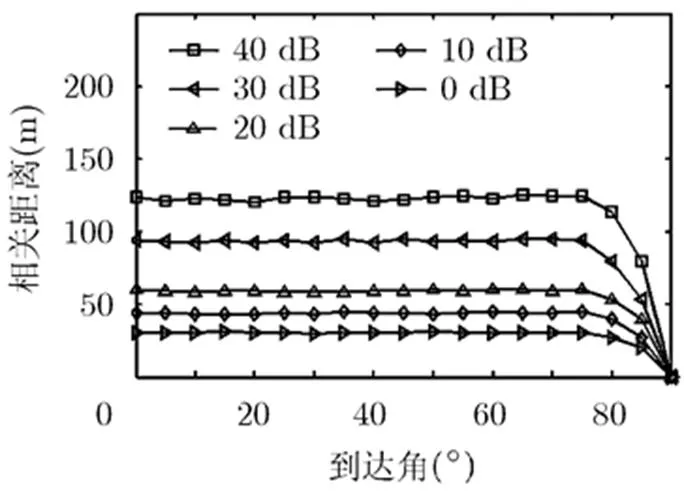
图4 杂波的相关距离

5.2实验2：杂波场景的重构

图5 实际杂波场景

图6 重构杂波场景

如图5~图7所示，通过稀疏重构的方式可以较精确地重构出场景中的强杂波块，而强杂波块对目标的检测有着重大影响，因此本文通过发射全向的正交信号感知观测场景并将获取的杂波信息用于随后的空时自适应处理是可行的。

5.3 实验3：空时自适应处理

探测阶段，对波束指向为-23°，杂噪比为40 dB的回波数据，分别采用最优处理器，FMLACC[12]以及本文方法进行处理。FMLACC方法是典型的预白化类STAP方法，且在先验协方差矩阵准确的情况下，该算法很快收敛。实验时，本文算法以及FMLACC算法的样本数分别为10个和40个。FMLACC算法的先验协方差矩阵可按如下方式构造：杂波的空时导向矢量是精确的，但是利用先验知识估计的杂波强度与真实的杂波强度存在一定的偏差。根据文献[15]，当外界环境改变时，利用先验知识估计的杂波强度可能会严重偏离真实的杂波强度。因此，本文假设估计的杂波强度与真实的杂波强度相差30 dB。

一般空时滤波器的性能用杂波改善因子IF来衡量，其定义为输出信杂噪比和输入信杂噪比的比值：

图8(a)~8(d)给出了最优处理器、FMLACC以及本文算法在不同平台位移下的杂波改善因子。对于FMLACC算法，当先验知识不准确时，预白化后的杂波子空间依然较大，导致该算法的收敛速度变慢，故本实验中FMLACC算法的性能并不理想。而本文算法由于通过实时获取的杂波信息构造杂波协方差矩阵，实现检测单元杂噪协方差矩阵较精确地估计，因此可以明显改善雷达在非均匀环境中的杂波抑制性能。但是当平台的空间位移量大于杂波的相关距离时(本实验中，杂波的相关距离为60 m左右)，感知阶段获取的杂波信息与实际杂波信息存在较大偏差，导致杂噪协方差矩阵的估计精度严重下降，故本文算法会有较大的性能损失。因此当平台的位移量大于杂波相关距离时，系统需重新感知场景，以完成杂波信息的实时更新。

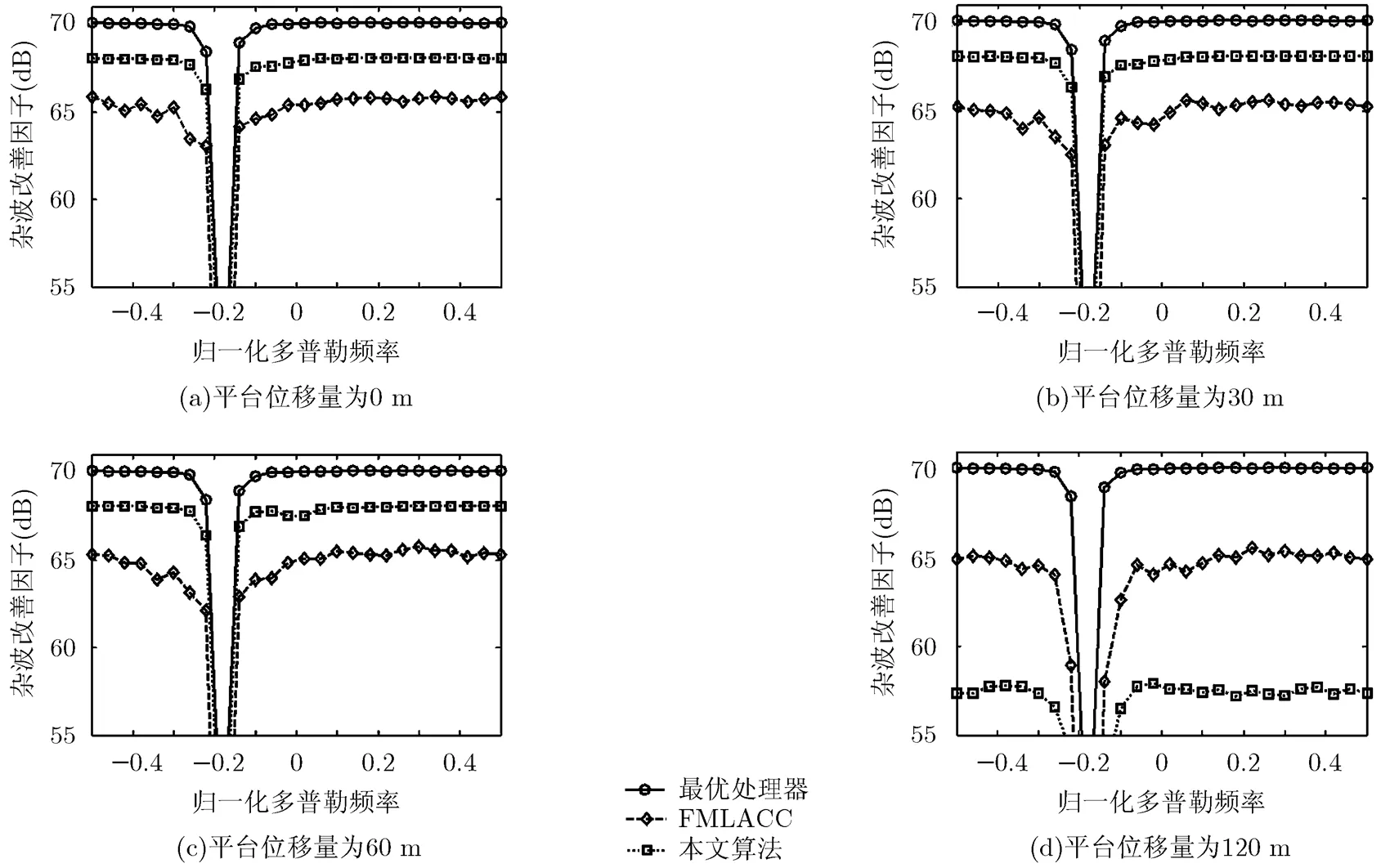
图8 杂波改善因子(第350个距离单元)

6 结束语

本文研究了在缺乏准确先验知识的情况下抑制非均匀杂波的问题，提出一种基于环境动态感知的空时自适应处理方法。该方法首先通过发射一组正交信号感知观测场景获取杂波信息；然后利用杂波信息结合平台参数及系统参数预测未来一段时间内杂波的协方差矩阵；最后将预测的协方差矩阵与样本协方差矩阵进行组合以构造空时滤波器，抑制杂波，提高输出信杂比。仿真结果表明，在缺乏准确先验知识的情况下，该方法依然可以有效地抑制非均匀环境中的杂波。然而，本文在重构场景时，假设场景内的强杂波是稀疏的，因此未来的一个研究方向是进一步提高重构算法对稀疏度的稳健性。

参考文献

[1] Ward J. Space-time adaptive processing for airborne radar[R]. MASS: Lincoln Lab, 1994.

[2] 范西昆, 曲毅. 知识辅助机载雷达杂波抑制方法研究进展[J]. 电子学报, 2012, 40(6): 1199-1206.

Fan Xi-kun and Qu Yi. An overview of knowledge-aided clutter mitigation methods for airborne radar[J]., 2012, 40(6): 1199-1206.

[3] Wang P, Wang Z, Li H,.. Knowledge-aided parametric adaptive matched filter with automatic combining for covariance estimation[J]., 2014, 62(18): 4713-4722.

[4] He M and Cao J. Recursive KA-STAP algorithm based on QR decomposition[C]. International Workshop on Microwave and Millimeter Wave Circuits and System Technology, Chengdu, China, 2013: 391-394.

[5] 阳召成, 黎湘, 王宏强. 基于空时功率谱稀疏性的空时自适应处理技术研究进展[J]. 电子学报, 2014, 42(6): 1194-1204.

Yang Zhao-cheng, Li Xiang, and Wang Hong-qiang. An overview of space-time adaptive processing technology based on sparsity of space-time power spectrum[J]., 2014, 42(6): 1194-1204.

[6] Melvin W and Showman G. An approach to knowledge-aided covariance estimation[J]., 2006, 42(3): 1021-1042.

[7] Capraro C, Capraro G, Bradaric Ivan,.. Implementing digital terrain data in knowledge-aided space-time adaptive processing[J]., 2006, 42(3): 1080-1099.

[8] 王旭, 纠博, 刘宏伟, 等. 一种基于先验信息的MIMO雷达发射方向图设计方法[J]. 电子与信息学报, 2013, 35(12): 2802-2808.

Wang Xu, Jiu Bo, Liu Hong-wei,.. A beampattern design method for MIMO radar based on a priori information[J].&, 2013, 35(12): 2802-2808.

[9] Hua G and Abeysekera S. Receiver design for range and doppler sidelobe suppression using MIMO and phased-array radar[J]., 2013, 61(6): 1315-1326.

[10] Khan W, Qureshi I, and Sultan K. Ambiguity function of Phased-MIMO radar with colocated antennas and its properties[J]., 2014, 11(7): 1220-1224.

[11] Chen X, Zhou P, Hou Q,.. Design of 2-D MIMO antenna arrays for high resolution burden surface[C]. The 11th IEEE International Conference on Electronic Measurement & Instruments, Harbin, China, 2013: 895-900.

[12] Wu Y, Tang J, and Peng Y. On the essence of knowledge- aided clutter covariance estimate and its convergence[J].,2011, 47(1): 569-585.

[13] Zhu X and Bamler R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J].,2012, 50(1): 247-258.

[14] Fishler E, Haimovich A, Blum R,.. Spatial diversity in radars-models and detection performance[J]., 2006, 54(3): 823-838.

[15] Skolnik M. 周万幸, 马林, 胡明春, 等. 雷达手册[M]. 第3版, 北京: 电子工业出版社, 2010: 644-655.

Space-time Adaptive Processing via Dynamic Environment Sensing

Fang Ming①Liu Hong-wei①Dai Feng-zhou①Wang Xiao-mo①②

①(,,710071,)②(,100041,)

In heterogeneous clutter environments, Space-Time Adaptive Processing (STAP) shows notable performance degradation for lacking sufficient Independent Identically Distributed (IID) training samples. To solve this problem, a STAP approach is proposed based on dynamic environment sensing. With transmitted signal being orthogonal waveform, the clutter information is achieved. Then the clutter information and platform parameters are used and a clutter covariance matrix at future time is obtained incorporating system parameters. Finally, the space-time processor can be built based on the combination of the predicted clutter covariance matrix and the sample covariance matrix. The simulation results demonstrate that the new approach still can achieve better clutter suppression performance under circumstance of inaccurate environmental knowledge.

Airborne radar; Clutter suppression; Space-Time Adaptive Processing (STAP); Sensing; Orthogonal signal

TN959.73

A

1009-5896(2015)08-1786-07

10.11999/JEIT141505

戴奉周 fzdai@xidian.edu.cn

2014-11-27收到，2015-05-11改回，2015-06-09网络优先出版

国家自然科学基金(61271291, 61201285)，新世纪优秀人才支持计划(NCET-09-0630)，全国优秀博士学位论文作者专项资金(FANEDD- 201156)和中央高校基本科研业务费专项资金资助课题

方 明： 男，1987年生，博士生，研究方向为认知雷达、空时自适应处理、目标检测.

刘宏伟： 男，1971年生，博士，教授，博士生导师，研究方向为雷达信号处理、雷达自动目标识别等.

戴奉周： 男，1978年生，博士，讲师，研究方向为统计与自适应信号处理及其在雷达信号处理和目标检测中的应用.

王小谟： 男，1938年生，教授，博士生导师，中国工程院院士，主要研究方向为雷达信号处理等.