回转窑截面物料运动及力链结构的数值试验

陈辉，刘义伦，肖友刚，李松柏



回转窑截面物料运动及力链结构的数值试验

陈辉1，刘义伦1，肖友刚2，李松柏1

(1. 中南大学机电工程学院，高性能复杂制造国家重点实验室，湖南长沙，410083;2. 中南大学交通运输工程学院，湖南长沙，410075)

采用离散单元法从颗粒尺度建立回转窑内物料的运动模型，以球形沙粒为例，通过数值计算，研究回转窑截面上物料的运动模式和力链结构。以Froude数、物料填充角、窑壁摩擦因数为变量，模拟物料的滑移、塌落、滚落、泻落、抛落和离心6种运动模式，模拟结果与实验观测结果相符。研究结果表明：回转窑内物料力链由表层弱力链区域(约占料层厚度10%)和底层强力链区域组成；滑移、塌落、滚落和泻落4种模式中，底层强力链结构稳定，颗粒之间相对静止，表层弱力链断裂和重组频繁，具体运动模式由窑转速和表层力链断裂重组的速度决定；实际转速中，泻落模式的物料颗粒碰撞最强烈。

回转窑；物料运动；力链；离散元法

回转窑是冶金、化工、建材等行业生产流程中的核心设备，应用于物料分解、烧结、干燥等物理化学反应过程[1]。大多数回转窑的物料呈散体颗粒状，其运动规律不仅决定着物料在窑内的停留时间，而且直接影响着窑内物料的混合与传热效率[2−3]。因此，回转窑内物料的运动规律一直是国内外研究的热点。通过实验测试和理论建模分析，学者们对回转窑内物料的运动规律展开了研究。Henein等[4]通过观察颗粒、石灰、碎石和铁珠在实验回转窑内的运动行为，将回转窑内物料运动模式主要分为：滑移、塌落、滚落、泻落、抛落和离心运动。Mellmann[5]和Ding等[6]基于连续介质力学理论，通过建立物料力矩平衡和质量守恒方程，对以上几种物料运动模式之间转换关系进行研究并建立了数学模型。工业生产中，一般认为滚落运动最利于物料的混合与热量的传递，是工程实践中的理想工况[7]。针对回转窑物料滚落运动产生的条件以及滚落运动中“运动层”和“静止层”厚度的研究，学者们也开展了实验测量并建立了相应的数学模 型[8−10]。回转窑物料属于散体颗粒物质体系，力学性能具有复杂的非线性和多变性特点[11]，一般的连续介质分析方法过分依赖高度简化的本构模型，易造成分析物料传力与运动时结果与实际相偏离。离散单元法作为分析散体物质力学行为的一种数值方法，能够提供散体内部的力学信息，虽然在回转窑方面的研究比较少见，但在岩土工程和粉体工程中已得到较广泛应用，目前已逐渐成为散体颗粒物质研究工作的主 流[12]。同时，为突破传统的颗粒物质力学理论框架限制，近20年提出了“力链”的概念[13]，认为力链是颗粒物质受力、变形和运动的内在因素[14−15]，关于颗粒物质体系力链的研究也成为当前科学研究的前沿。本文作者采用离散单元法从颗粒尺度建立回转窑内物料运动的数学模型，通过数值试验，对物料运动规律进行分析，并研究运动过程中物料颗粒的力链结构。

1 数值试验建模

1.1 颗粒离散元模型

针对回转窑物料的散体颗粒性质，离散元法中以离散颗粒的力学理论，配合经典的牛顿第二运动定律及合适的时间积分法来描述物料颗粒的运动。离散元本构关系体现于力与位移的关系，材料参数具有明显的物理意义，对于数目稠密的颗粒物料流而言，是理想的分析方法。

假设回转窑物料由颗颗粒组成，根据牛顿第二定律，可得到第(=1, 2, …,)颗物料的运动控制方程：

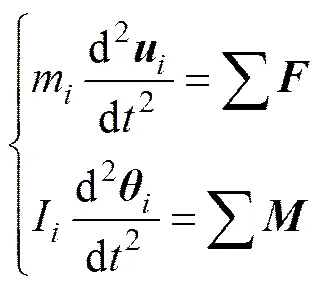
其中：为时间变量；m和I分别为物料颗粒的质量与转动惯量；和分别为物料颗粒的速度矢量与角速度矢量；为物料颗粒在质心处受到的合外力，包括壁面和物料颗粒(=1, 2, …,−1,+1, …,)对颗粒的接触力、物料颗粒重力；为物料颗粒所受合力矩，包括壁面和颗粒作用在颗粒上的接触切向力矩和滚动力矩。

物料颗粒的接触本构模型是离散元法的核心，本研究中将回转窑物料近似为均匀的球形颗粒，以圆球单元为研究对象。如图1所示，物料颗粒所受合外力与合外力矩采用Hertz-Mindlin接触刚度型，物料颗粒的控制方程式(1)采用差分法求解，最后通过时间步进积分计算得到物料颗粒位置、速度和受力随时间的变化[11]。离散元法可以方便的提取颗粒力学信息，图1中，连接颗粒中心和接触点的矢量便形成颗粒之间的力链，矢量大小由线条的粗细表示，正比于接触强度(≥0)。

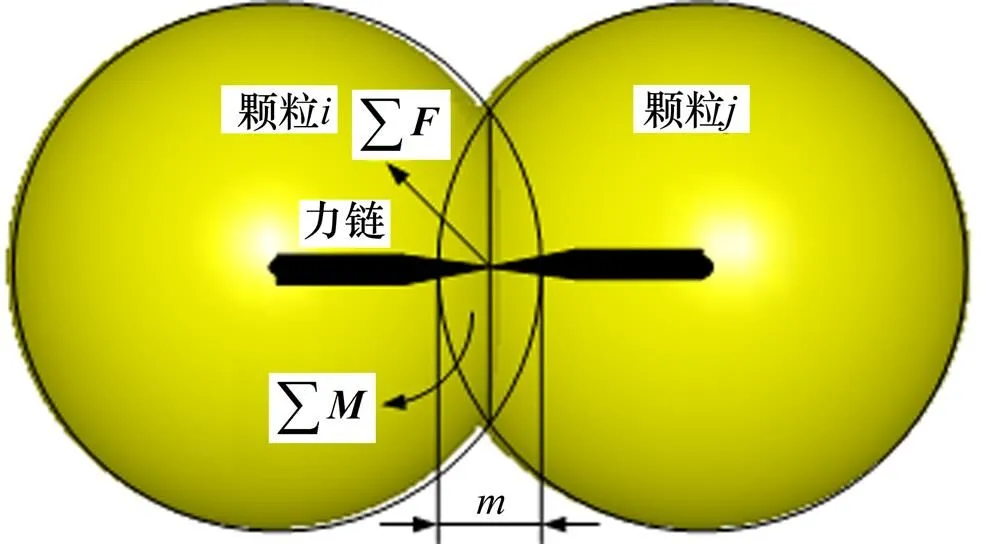
图1 颗粒离散元接触模型示意图

1.2 物料运动建模

本文物料颗粒采用球形沙粒，颗粒直径呈正态分布。表1所示为离散元数值模拟参数。

表1 数值模拟参数

回转窑运行中窑轴线为水平状态。根据以往学者研究习惯，回转窑运行状态采用物料填充率和Froude数表示[2]，且

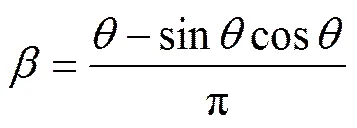
(3)

由于Mellmann[5]在实验中发现窑端面挡板会使同一运动模式下的Froude数偏小，为消除窑端面挡板对物料运动的影响，模型中不设置挡板，轴线方向为循环边界，即回转窑窑前端面的物料与后端面的物料相接触。

图2(a)所示为采用离散元方法生成的物料静态堆积三维示意图，图中物料填充率=0.5，回转窑将绕轴线顺时针转动，从而带动物料运动。图2(b) 所示为力链结构。本文借鉴Sun等[14]对强力链的判断准则，定义接触强度大于平均接触强度的力链为强力链并标记为红色，弱力链为浅灰色，图2(b)中实线表示物料表层界面，虚线表示强力链区域与弱力链区域的分界面。由图2(b)可知：物料内部力链呈非规则的网络状，具有非均匀和各向异性的特点；力链沿着重力方向逐渐变强，且按照本文的对强力链的定义和描述，物料表层为弱力链区域，主要由弱力链组成，约占料层厚度的10%，底层为强力链区域，由起支撑作用的强力链和起辅助作用的弱力链组成。

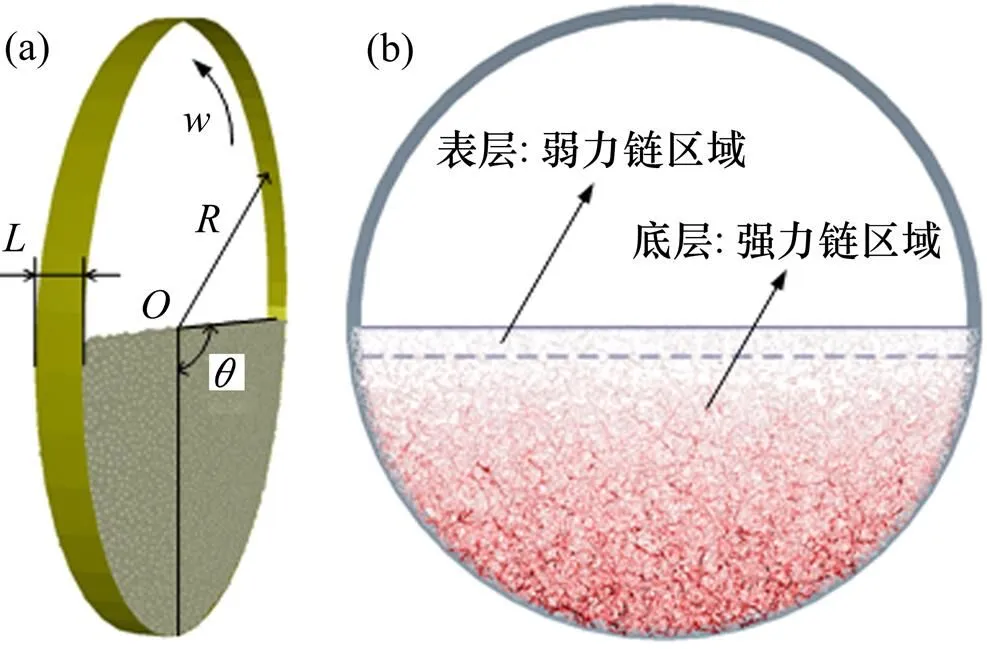
(a) 三维示意图；(b) 力链结构

2 物料的运动模式

针对回转窑截面上物料运动规律的研究，Henein等[4−5]在实验回转窑上进行了大量实验测试，将运动模式划分为6种：滑移、塌落、滚落、泻落、抛落和离心运动。其中Mellmann[5]通过对实验结果的统计，以Froude数、物料填充率、内壁摩擦因数为主要变量，将物料6种运动模式对应的变量取值区域进行了划分。

本文以，和为主要变量，参照Mellmann的变量取值区域对回转窑内物料的运动模式进行数值模拟，计算结果与Mellmann的实验观测结果相符，证明本文的离散元模型能有效分析回转窑截面上的物料运动规律。图3所示为其中一组变量取值模拟而得到的6种物料运动形态，回转窑顺时针转动，图3中实线表示物料表层界面，物料颗粒用颗粒中心的速度矢量表示，速度与颜色深度成正比。

1) 图3(a)所示为滑移，由于偏小，物料在达到最大动态安息角U之前以整体的形式在窑壁内往返滑动，颗粒速度与窑半径成正比。

2) 当足够大，且10−5＜＜10−3时，出现图3(b)所示的塌落运动，物料随窑的旋转不断被提升，表层颗粒间歇式从最大动态安息角U高速崩落至最小动态安息角L，底层颗粒随窑旋转并且相对窑壁静止。

3) 随着窑转速增大(10−4＜＜10−2)，表层颗粒由间歇式崩落变为连续滚落，并形成稳定的高速运动层，底层颗粒随窑旋转并且相对窑壁静止，得到图3(c)所示的滚落运动。

4) 图3(d)所示为泻落运动。与滚落相似，只是由于窑转速进一步增大(10−3＜＜10−1)，表层颗粒界面变成了“弓形”。

以上为物料在回转窑中几种常见的运动模式。

5) 当10−3＜＜10−1时，图3(e)所示的抛落运动出现，物料翻滚剧烈，且有颗粒甩入空中，已经没有明显的表层界面。当＞1时，出现图3(f)所示的离心运动，颗粒紧贴窑壁并相对静止，形成稳定的环形物料圈。

(a) Fr=0.000 1, μ=0.25, β=0.4; (b) Fr=0.000 9, μ=0.42, β=0.4; (c) Fr=0.009, μ=0.42, β=0.4; (d) Fr=0.09, μ=0.42, β=0.4; (e) Fr=0.9, μ=0.42, β=0.4; (f) Fr=1.5, μ=0.42, β=0.4

除球磨机中可见抛落运动外，回转窑运行中几乎没有抛落和离心运动，因此，抛落和离心运动一般不是人们研究的重点。

3 物料的力链结构

颗粒间的力链结构反映了物料颗粒的宏观运动行为，图4所示为滑移模式的力链结构。图4(a)描述了物料滑移运动的内部的力链分布，图4(a)中物料的底层强力链和表层弱力链在运动中都没有破坏，所以，虽然底层物料颗粒与窑壁有相对运动，但由于颗粒之间的力链结构稳定，从而颗粒之间相对位置稳定，物料以整体的形式滑动。图4(b)所示为底层颗粒力链局部放大图，图中，，和为4个力链节点，观察点固定在物料上。由图4(b)可知：物料随着窑转动，重力与力链网络之间的夹角改变，力链的强度轻微变化，但，，和4个节点稳定，由于偏小，物料滑移回同一位置时，力链强度也恢复到原来状态，表层力链变化与底层类似，整个过程物料相当于单一的整体。

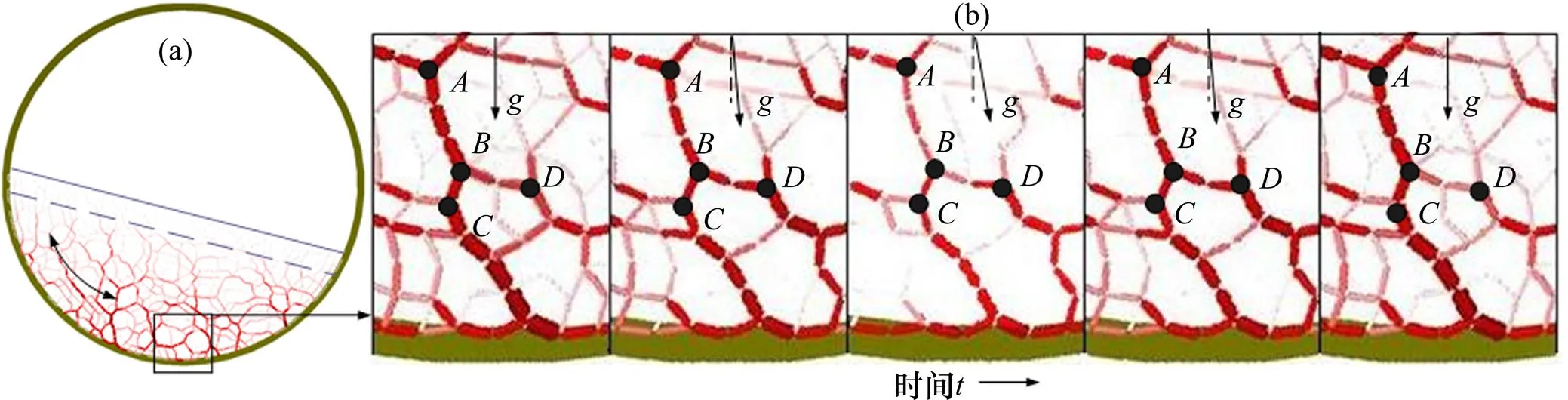
(a) 力链截面图；(b) 局部放大图

图5所示为塌落模式的力链结构。图5(a)描述了物料塌落运动的力链分布情况。从图5(a)可见：当足够大时，物料随窑转动不断被提升；当物料表面倾角达到U时，表层弱力链区域被重力破坏，导致颗粒从高端向下崩落并进行重组，处于高端的部分强力链进入表层，形成新的表层弱力链区域，物料表面倾角变为L；当表面倾角重新达到U时，表层弱力链再次破坏而导致物料颗粒崩落，如此循环。图5(b)所示为强、弱力链区域交界处力链断裂过程的局部放大，图中，，和为4个力链节点，观察点固定在物料上；物料随着窑的旋转，颗粒力链网络与重力的夹角不断增大，在重力剪切作用下，表层弱力链断裂后，点，和点，所处强力链逐渐变弱、变形、进入表层后替代弱力链，最后依次断裂消失。力链的重组与图5(b)所示的断裂过程相反，但是形成的力链结构是随机的。在整个过程中，底层强力链区域由于抵御剪切破坏的能力较强，力链结构稳定，颗粒之间没有相对位移。

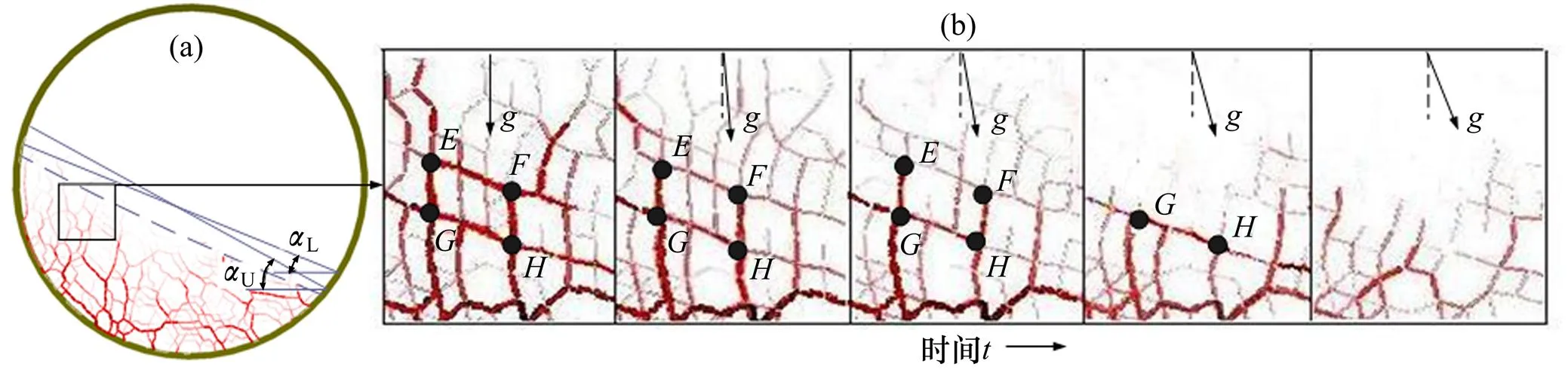
(a) 力链截面图；(b) 局部放大图

为方便描述，设强力链替代表层弱力链的时间为r，r主要由窑转速决定，且

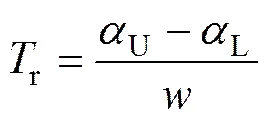
设表层弱力链从断裂到重组的时间为b，当窑转速较低，r＞b时，表层颗粒崩落的速度大于被底层颗粒替代的速度，物料为间歇式崩落，即塌落模式。

图6(a)所示为滚落模式的力链结构。与塌落模式力链结构相似，表层区域力链频繁断裂重组，而底层的强力链结构稳定。只是由于增大，使r=b，物料表层力链由间歇式破坏变成连续的断裂与重组，形成稳定的颗粒运动层，即以往学者描述的“运动层”，底层力链结构稳定，颗粒相对静止，即为“静止层”。并且结合图3(c)和图6(a)可知：采用文中对强、弱力链的描述方法，回转窑物料表层的“运动层”与的弱力链区域的厚度相吻合。

图6(b)所示为泻落模式的力链结构。其力链结构与滚落相似，只是表面弱力链区域变成“弓形”，并且区域的高端变厚，这是由于进一步增大，r＜b时，底层颗粒替代表层颗粒的速度超过表层颗粒崩落速度而导致。

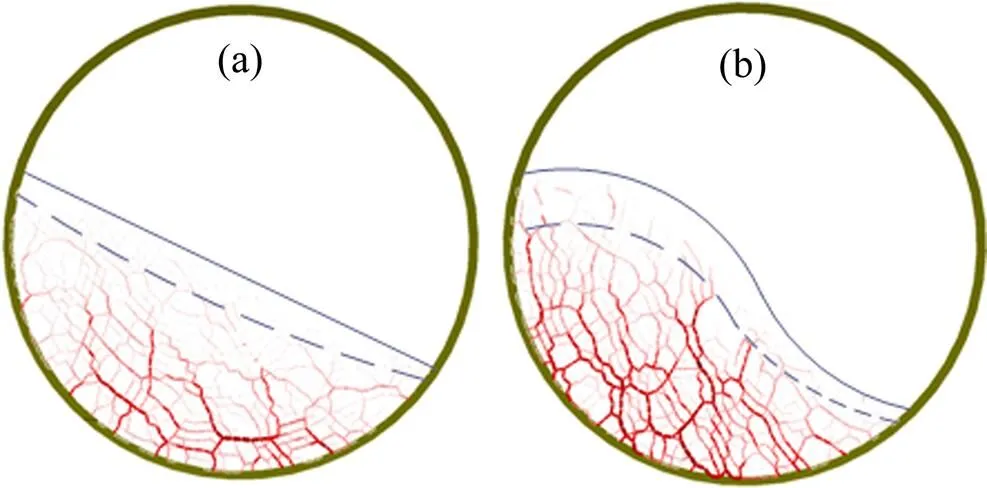
(a) 滚落模式；(b) 泻落模式

结合以上分析：物料在回转窑几种常见运动模式中，底层强力链结构稳定，颗粒不发生相对运动，表层弱力链在重力作用下被破坏，导致颗粒向下滚动。具体运动模式由r和b决定，若将滑移状态的r视为无穷大，则：当r→∞时，物料为塌落运动；当r＞b时，物料为塌落运动；当r=b时，物料为滚落运动；当r＜b时，物料为泻落运动。

图7(a)所示为抛落的力链结构。由于离心力作用，强力链变得不连续，物料内部力链网络已经不稳定，导致物料内部混合剧烈。图7(b)所示为离心运动的力链结构。颗粒沿窑壁形成一圈环形的稳定力链，使物料固定在窑壁上，形成离心运动。

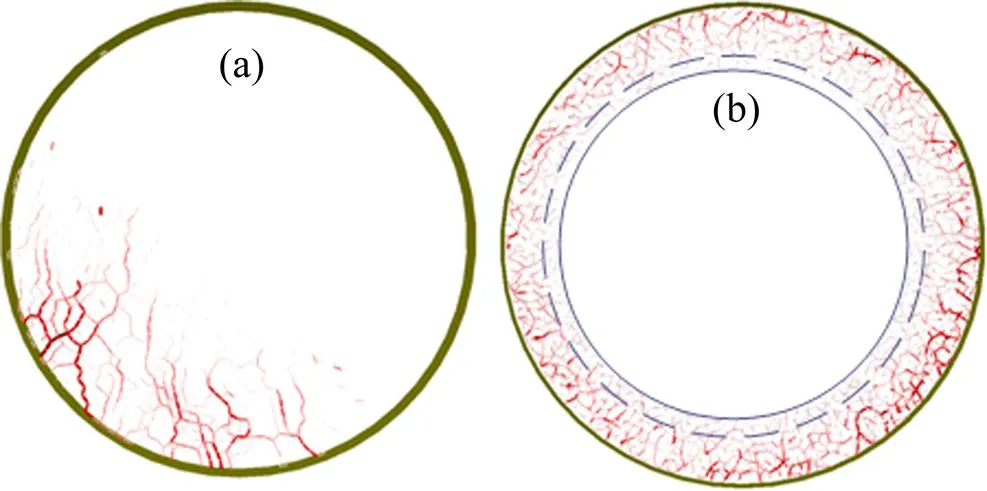
(a) 抛落模式；(b) 离心模式

力链断裂和重组越频繁，颗粒的相对运动和碰撞越剧烈。力链的断裂和重组伴随着颗粒接触数量的变化，图8所示为6种运动模式下颗粒接触数变化的对比。由图8可知：滑移和离心运动的颗粒接触数量稳定；塌落的颗粒接触数为间歇式变化；滚落、泻落和抛落的颗粒接触数为连续变化且程度依次增强。结合回转窑实际转速范围，物料颗粒相对运动和碰撞最剧烈的运动模式为泻落模式。

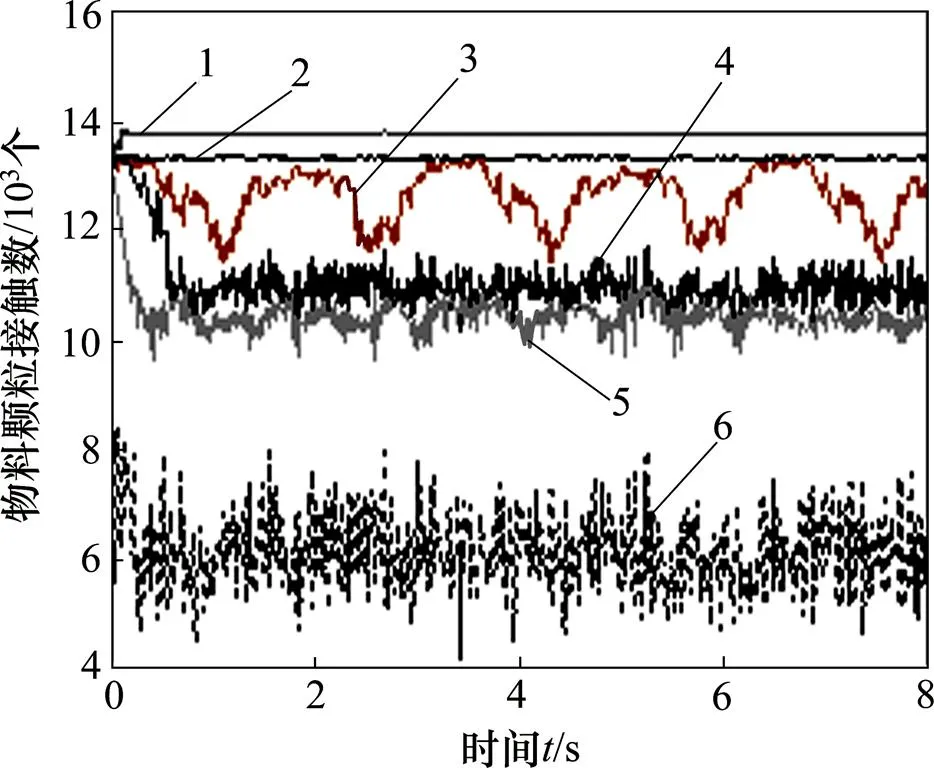
1—离心；2—滑移；3—塌落；4—滚落；5—泻落；6—抛落

4 结论

1) 基于离散元法建立的物料运动模型模拟了滑移、塌落、滚落、泻落、抛落和离心6种运动模式，据此模型能有效分析物料在回转窑内的运动规律。

2) 回转窑内物料的力链分为表层弱力链区域和底层强力链区域，表层弱力链区域容易发生力链的变形与断裂。

3) 常见的滑移、塌落、滚落和泻落4种运动模式中，底层物料的强力链结构稳定，物料颗粒之间相对静止，表层物料的弱力链发生断裂和重组，物料颗粒高速向下运动，具体运动模式由强力链替代表层弱力链的时间r和表层力链从断裂到重组的时间b决定；抛落模式下，物料整体力链不稳定，而离心模式的颗粒沿窑壁形成一圈环形的稳定力链。

4) 在实际运行工况中，泻落运动模式下物料力链的断裂与重组最频繁，颗粒之间的相对运动和碰撞最剧烈。

参考文献：

[1] Herz F, Mitov I, Specht E, et al. Experimental study of the contact heat transfer coefficient between the covered wall and solid bed in rotary drums[J]. Chemical Engineering Science, 2012, 82: 312−318.

[2] Mellmann J, Specht E, LIU Xiaoyan. Prediction of rolling bed motion in rotating cylinders[J]. AIChE Journal, 2004, 50(11): 2783−2793.

[3] Marigo M, Cairns D L, Davies M, et al. A numerical comparison of mixing efficiencies of solids in a cylindrical vessel subject to a range of motion[J]. Powder Technology, 2012, 217: 540−547.

[4] Henein H, Brimacombe J K, Watkinson A P. The modeling of transverse solids motion in rotary kilns[J]. Metall Urgical Transactions B, 1983, 14: 207−220.

[5] Mellmann J. The transverse motion of solids in rotating cylinders-forms of motion and transition behavior[J]. Powder Technology, 2001, 118: 251−270.

[6] Ding Y L, Forster R, Seville J P K, et al. Granular motion in rotating drums: bed turnover time and slumping-rolling transition[J]. Powder Technology, 2002, 124: 18−27.

[7] Demagh Y, Moussa H B, Lachi M, et al. Surface particle motions in rotating cylinders: Validation and similarity for an industrial scale kiln[J]. Powder Technology, 2012, 224: 260−272.

[8] CHENG Niansheng, ZHOU Qi, Tan S K, et al. Application of incomplete similarity theory for estimating maximum shear layer thickness of granular flows in rotating drums[J]. Chemical Engineering Science, 2011, 66: 2872−2878.

[9] LIU Xiaoyan, Specht E. Predicting the fraction of the mixing zone of a rolling bed in rotary kilns[J]. Chemical Engineering Science, 2010, 65: 3059−3063.

[10] Specht E, SHI Yichun, Woche H, et al. Experimental investigation of solid bed depth at the discharge end of rotary kilns[J]. Powder Technology, 2010, 197: 17−24.

[11] 曹秒艳, 董国疆, 赵长财. 基于离散元法的固体颗粒介质传力特性研究[J]. 机械工程学报, 2011, 47(14): 62−69. CAO Miaoyan, DONG Guojiang, ZHAO Changcai. Research on pressure-transfer characteristics in the solid granule medium forming based on the discrete element method[J]. Journal of Mechanical Engineering, 2011, 47(14): 62−69.

[12] Manickam S S, Shah R, Tomei J, et al. Investigating mixing in a multi-dimensional rotary mixer: Experiments and simulations[J]. Powder Technology, 2010, 201: 83−92.

[13] Bouchaud J P, Cates M E, Claudin P. Stress distribution in granular media and nonlinear wave equation[J]. J Phys, 1995, 5: 639−656.

[14] Sun Q C, Wang G Q, Hu K H. Some open problems in granular matter mechanies[J]. Soil and Foundations, 1972, 12(1): 523−529.

[15] Walsh S D C, Tordesillas A, Peters J F. Development of micromechanical models for granular media: The projection problem[J]. Granular Matter, 2007, 9(5): 337−352.

Numerical experiments on transverse motion and force chains of solids in rotating cylinders

CHEN Hui1, LIU Yilun1, XIAO Yougang2, LI Songbai1

(1. State Key Laboratory of High Performance Complex Manufacturing, School of Mechanical and Electrical Engineering, Central South University, Changsha 410083 China;2. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

Taking account of the interactions between particles, a kinematic model of granular bed in rotating kiln was established using discrete element method based on its particle size. Using spherical quartz sand as bed material, transverse bed motions and particle force chains were studied through numerical calculation of the model. Taking the Froude number, filling angle, and wall friction coefficient as variables, six forms of transverse bed motion observed in experimental tests were simulated: sliding, slumping, rolling, cascading, cataracting and centrifuging. The results show that the force chains within the bed consist of two parts: the surface area with weak chain (about 10% of the bed thickness) and the underlying area with strong chain. In case of sliding, slumping, rolling and cascading, the force chains of the underlying area are stable and the particles are relatively static. However, the force chains of the surface area are broken and restructured frequently, which makes the material particles move downward and mix together. The specific motion is determined by rotate speed and force chain breaking-restructuring speed. Contracts between bed particles in the form of cascading are the most savage for actual operation.

rotating cylinders; transverse bed motion; force chains; discrete element method

10.11817/j.issn.1672-7207.2015.07.009

TF537

A

1672−7207(2015)07−2446−06

2014−07−08；

2014−10−13

国家自然科学基金资助项目(51374241，51275531)；中国博士后基金资助项目(20100471229，201104514)；湖南省科技计划项目(2012GK3171) (Projects(51374241, 51275531) supported by the National Natural Science Foundation of China; Projects(20100471229, 201104514) supported by the China Postdoctoral Science Foundation; Project(2012GK3171) supported by the Science and Technology Project of Hunan Province, China)

刘义伦，博士，教授，博士生导师，从事大型设备状态监测和诊断、离散物质传热传质机理研究；E-mail: ylliu@csu.edu.cn

(编辑 杨幼平)