可修系统不完全维修连续比例强度模型及应用
任丽娜,芮执元,王智明
可修系统不完全维修连续比例强度模型及应用
任丽娜1,芮执元1,王智明2
(1. 兰州理工大学机电工程学院,甘肃兰州,730050;2.淮海工学院机械工程学院,江苏连云港,222005)
为解决传统不完全维修模型难于工程应用的问题,基于边界强度过程理论,提出一种新的具有封闭形式解的连续比例强度模型。讨论模型的特性,推导模型参数及诸如给定时刻的条件可靠度、期望故障数、累积平均故障间隔时间等重要可靠性指标的极大似然点估计的计算公式,利用Fisher信息矩阵法和delta法给出模型参数及上述可靠性指标的区间估计,基于Akaike信息准则和拟合优度检验指标,给出模型评价准则。以数控机床现场故障数据为例对所提方法进行验证。研究结果表明:应用本文方法可以获得数控机床可靠性指标封闭形式的解及置信区间,可以很好地应用于工程实际。
不完全维修;连续比例强度模型;边界强度过程;极大似然估计;可修系统
对于可修系统,当其发生故障后,通常需经过维修才能使其恢复至功能状态。根据维修的影响程度,通常假设维修可使系统恢复至“修复如新”(完全维 修[1])、“修复如旧”(最小维修[2−3])和“好于旧而次于新”(不完全维修[4−5])3种状态,由于不完全维修假设同时考虑了运行时间和维修行为对系统状态的影响,因此更符合工程实际。常见的不完全维修模型主要有2种:虚龄模型[5]和比例强度模型[6]。虚龄模型由Kijima等[5]首次提出,认为维修效果可通过减小系统役龄来描述,有Kijima模型Ⅰ和Kijima模型Ⅱ 2种,模型参数求解方法主要有Monte Carlo(MC)仿真法[7]、极大似然估计法[8−9]、似然比检验法[10]、非线性约束规划法[11]等,但由于模型本身的非连续性,这些方法均难获得诸如条件可靠度、累积平均故障间隔时间等重要可靠性指标的封闭形式的解,因此,该模型很难用于解决工程实际问题。比例强度模型最早由Cox[6]提出,其强调通过强度减小系数来评估系统的维修水平,在Cox工作的基础上,Lawless等[12]提出既包含系统运行时间信息又包含更新类型行为的比例强度模型,但该模型同样存在难于应用的问题,鉴于此,Guo 等[13−14]提出将累积故障强度函数作为协变量引入比例强度模型,可以获得模型参数及可靠性指标封闭形式的解,但未给出条件可靠度等可靠性指标的置信区间,且模型中系统的基础故障强度过程主要由幂律过程(power law process, PLP)和对数线性过程(log-linear process, LLP)来描述,而对处于耗损期的可靠性恶化系统,由于频繁的被维修,其故障强度会随着时间的增加而趋于一稳定值,此时,边界强度过程[15]应该更适合描述其故障过程。因此,本文作者针对可用边界强度过程描述的性能恶化的可修系统,在综合考虑其故障过程、运行时间及维修历史等信息影响的情况下,提出了一种新的具有封闭形式解的连续比例强度模型,并给出了重要可靠性指标置信区间的求解方法。
1 模型建立
对于维修频繁的可靠性恶化系统,其经维修后一般会处于“好于旧而次于新”的中间状态,因此不完全维修模型更适合描述其实际的维修效果,且因其故障过程更适合用边界强度过程描述,因此,定义连续比例强度模型为

2 模型特性

(3)
显然,式(3)可大于0或小于0,其符号主要由基本故障强度模型参数及维修影响系数决定,若式(3)在时刻大于零,则为一增函数,即系统处于耗损阶段;若式(3)在时刻小于0,则为一减函数,即系统处于可靠性增长阶段;若式(3)接近于0,则系统具有稳定的故障强度。

将式(4)两边进行变换并取不定积分,得
(5)
通过对式(5)进行求解,可得
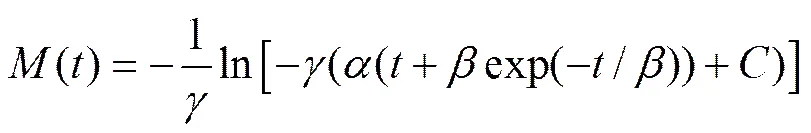
(7)

<(9)
3 模型参数及可靠性指标的极大似然点估计及区间估计
3.1 模型参数及可靠性指标的极大似然点估计
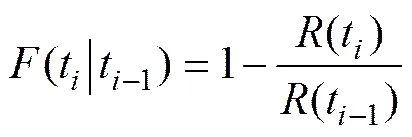
与式(1)中的新模型相对应的经验故障强度函数为
(11)
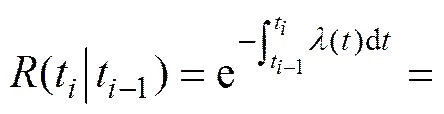
(12)
而第次故障时间t的条件概率密度函数为
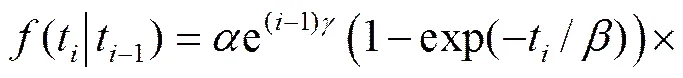
(13)
若故障数据为时间截尾,则似然函数为

式中:为试验结束时间。若故障数据为故障截尾,则=t,且。
那么,对于单个系统,当故障数据为时间截尾时,对数似然函数为

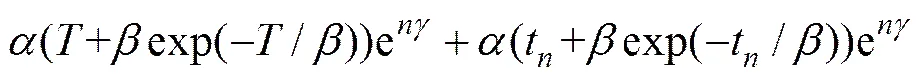
当故障数据为故障截尾时,对数似然函数为
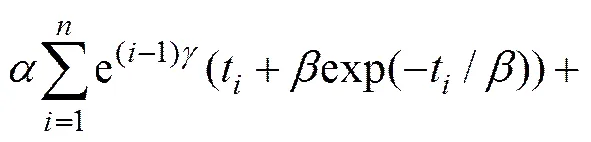
(16)

(17)
因此,将式(17)代入式(16)中可以得到1个含有2个参数的对数似然函数:
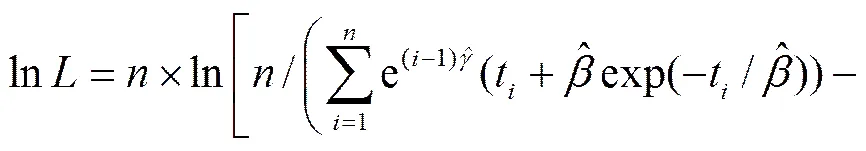
(18)
所以,在式(17)大于零的条件下,将式(18)最大化并作为目标函数,将参数估计问题转化为优化问题,即可求出模型参数和,再将其代入式(17),则可求出参数。对于单个系统,模型参数求解过程与上述方法相同。
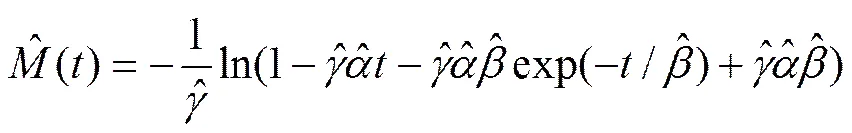
(20)
(21)
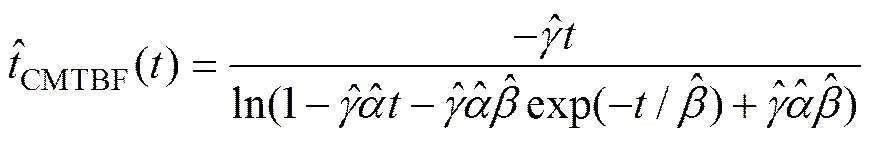
(23)
3.2 模型参数及可靠性指标的区间估计
在小样本(<30)情况下,若利用参数极大似然估计的渐近正态分布特性求置信区间会产生负的置信下限,而其渐近对数正态分布避免了这一问题,因此,若要求模型参数大于0,利用参数极大似然估计的渐近对数正态分布特性求置信区间更优。因此,模型估计参数或可靠性指标的置信区间可由下式求出:
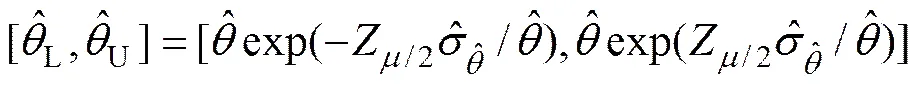
因此,只需求出待估计参数或可靠性指标的方差即可求出置信区间。根据Fisher信息矩阵法[16],单个系统故障截尾数据不完全维修模型参数,和的方差(var)和协方差(cov)可由逆Fisher矩阵给出,即
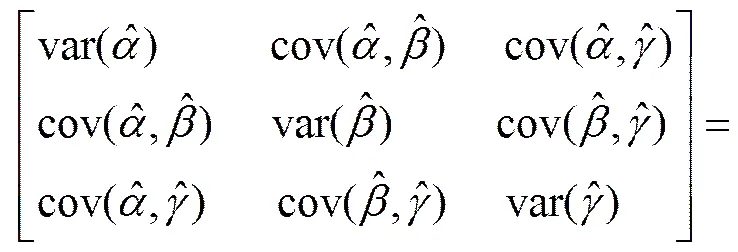
(25)
对式(16)中各模型参数求二阶偏导数得
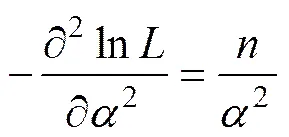
;
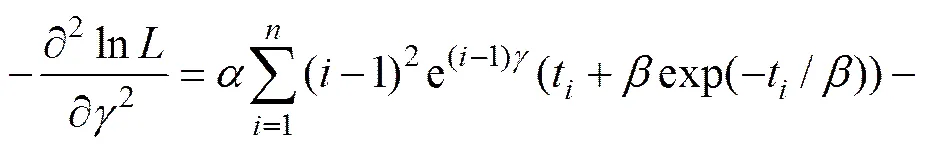
;
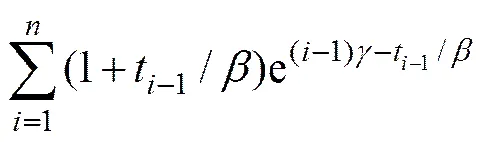
;
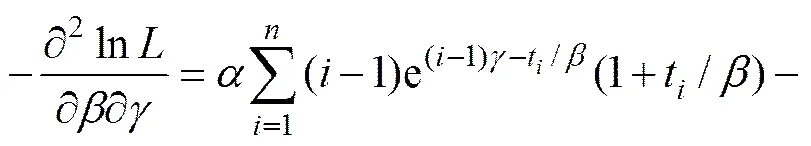
对于可靠性指标的置信区间,可以根据模型参数的方差及协方差求出。根据delta法[13],系统条件可靠度的方差为
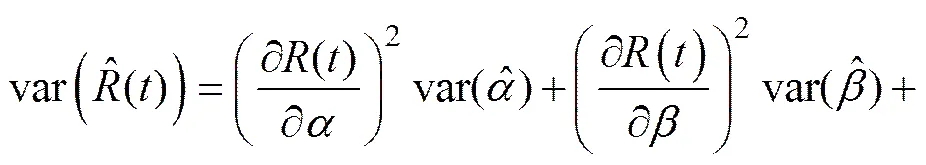
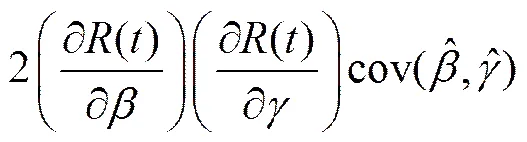
将上式中()用()等其他可靠性指标代替,即可求出相应可靠性指标的方差。
为使系统可靠度变换到[0,1]区间内,在计算可靠度区间上边界、下边界时引入logit函数,其表达式为
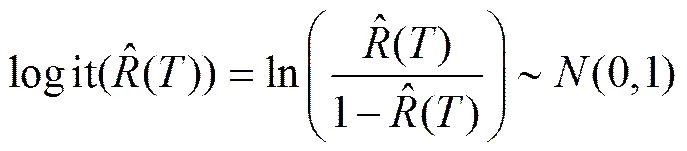
因此,可靠度置信区间计算公式为
将计算结果与式(24)进行比较,2种计算方法中上边界较小者为最终上边界,下边界较大者为最终下 边界。
4 实例分析
收集到国内某机床厂某一数控机床现场故障截尾数据20个,故障时间为950.46,1 405.2,1 515.92, 1 611.4,2 709.33,2 797.42,2 954.22,3 153.87,3 446.2,3 543.11,3 706.49,3 923.93,4 074.9,4 126.33,4 427.4,4 659.99,5 061.16,5 840.57,6 345.3,6 742.95 h。
那么,基于何种假设的模型最佳,最适合描述数控机床的故障过程,还需进行选择。Akaike信息准则法[17]是比较简单实用的模型选择方法之一,该准则利用似然估计性质,认为当Akaike信息准则(AIC)最小时,对应的模型即为最佳模型,其表达式定义为
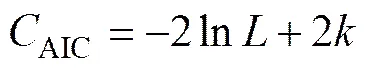
式中:为模型参数的个数;ln为故障数据的最大对数似然估计。
不同模型的AIC计算结果如表1所示,显然,本文模型的AIC最小,初步说明本文模型即为最佳模型。由此可知,该数控机床经维修后处于“好于旧而次于新”的中间维修状态,应基于不完全维修假设对其可靠性进行分析。为进一步验证所选模型即为最佳模型,可对模型进行拟合优度检验,定义拟合优度评价指标[18]为
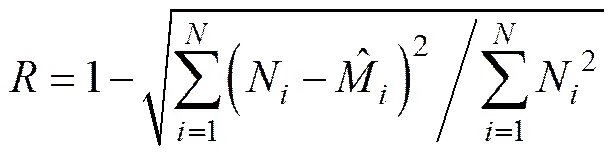
式中:N为时刻实际累积故障数;为期望故障数的估计值。越大则说明模型拟合程度越好。不同模型的拟合优度计算结果如表1所示。从表1可以看出:本文模型的拟合优度评价指标最大,进一步说明本文模型即为最佳模型。不同模型的累积故障数拟合曲线如图1所示,从图1可以看出:本文提出的连续比例强度模型更适合描述其故障趋势。

表1 不同模型计算结果
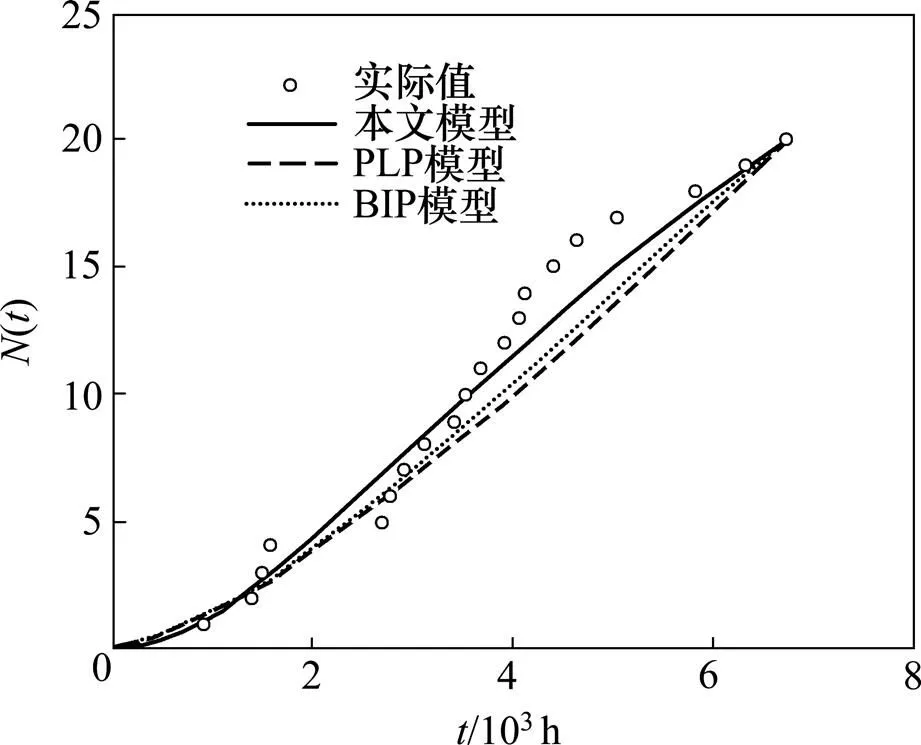
图1 不同模型累积故障数拟合曲线
本文模型故障强度曲线如图2所示。从图2可以看出:故障强度先增加后减小。故障强度增加可能是因为数控机床某部位故障时,其他部件虽在用但潜在的未揭露的故障增加的缘故,而后随着不断地维修,故障强度逐渐减小。系统条件可靠度与时间曲线、瞬时平均故障间隔时间曲线和累积平均故障间隔时间曲线分别如图3~5所示。从图3和图5可以看出:对处于耗损期的数控机床,由于频繁地对其进行维修,系统条件可靠度有了明显提高,但由于耗损增加,可靠度相对来说也在逐渐下降,累积平均故障间隔时间也逐渐缩短直至趋于稳定。由图4所示本文模型对应曲线可知:该机床大约从第5个故障开始,瞬时平均故障间隔时间逐渐增加,说明不完全维修效果显著,实现了机床的可靠性增长。而对于BIP模型,瞬时平均故障间隔时间一直处于逐渐减小的状态,维修并没有使系统可靠性得到明显改善,与本案例机床实际情况不符。
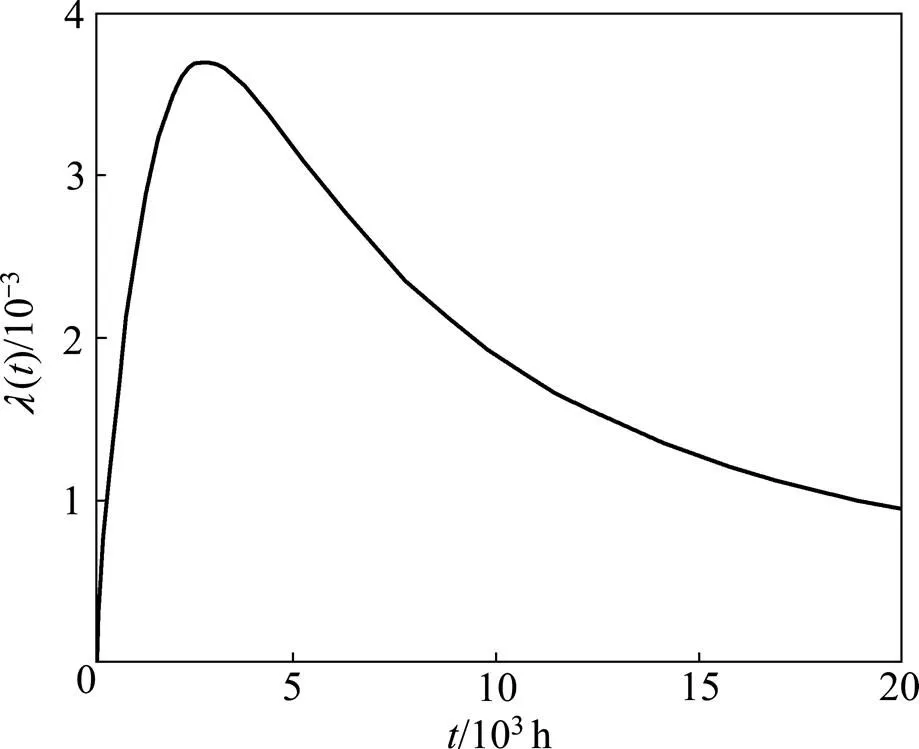
图2 新模型故障强度曲线
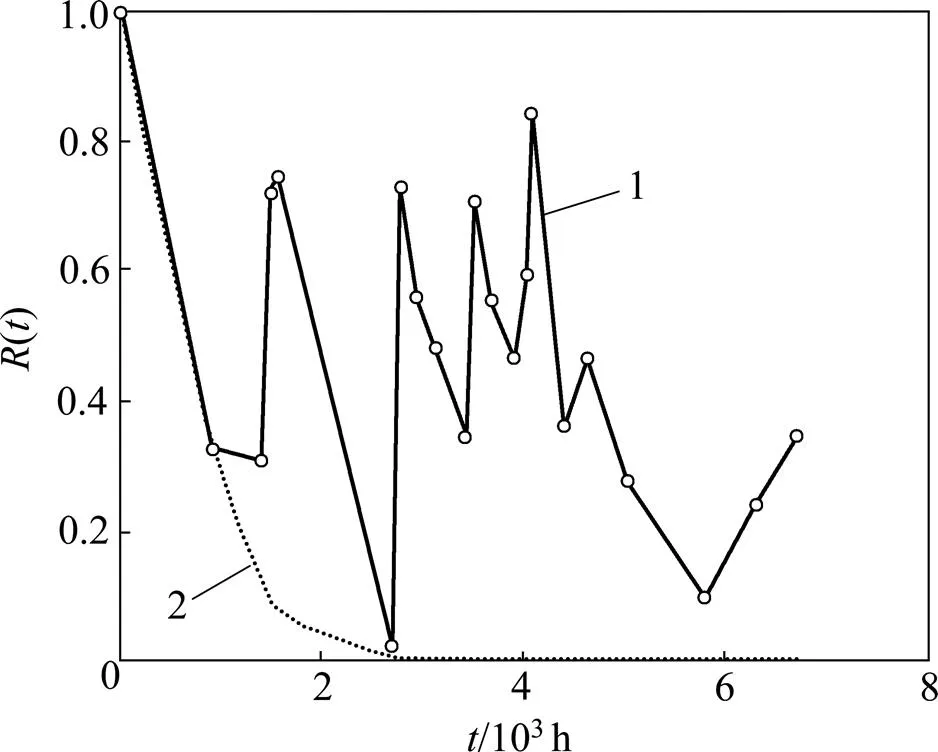
1—本文模型;2—BIP模型
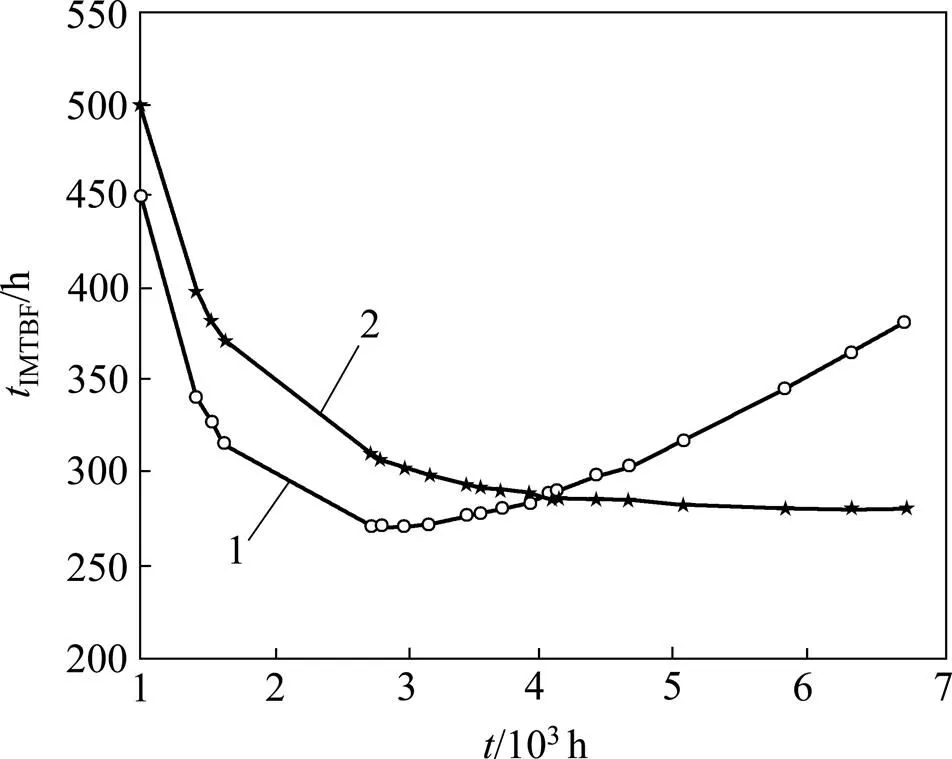
1—本文模型;2—BIP模型
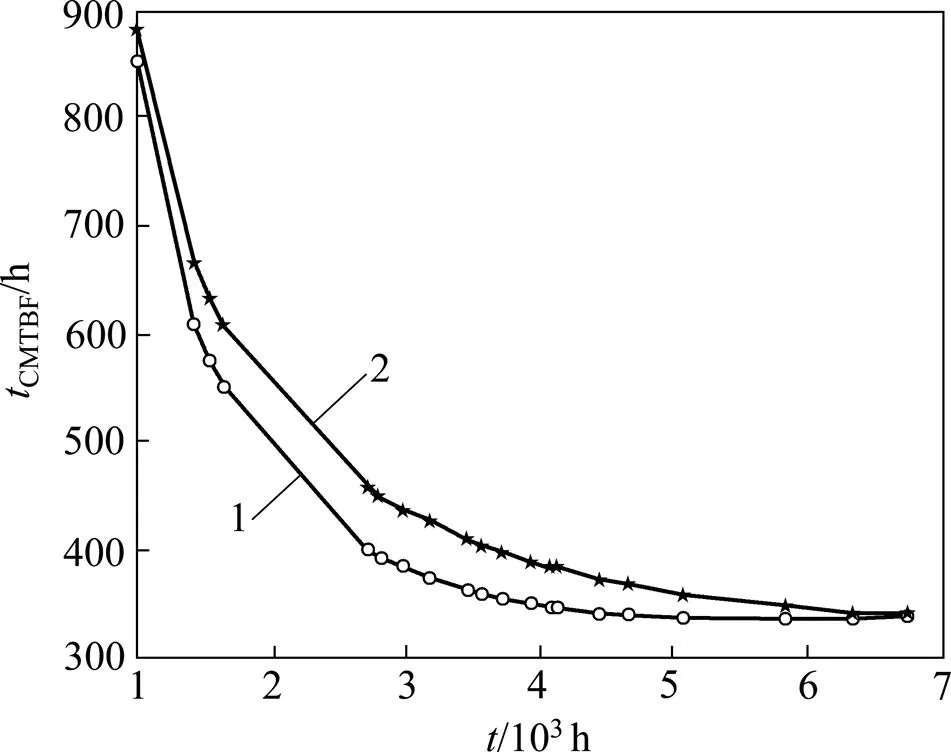
1—本文模型;2—BIP模型
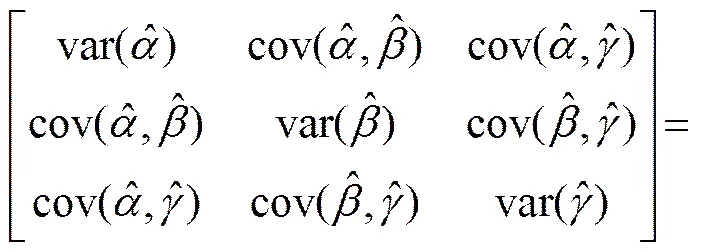
;
;
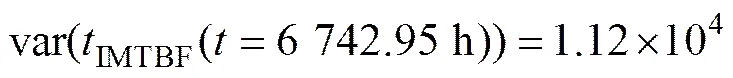
;
;
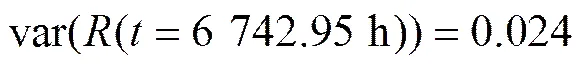
则模型参数和可靠性指标的点估计和置信度为95%的区间估计如表2所示。
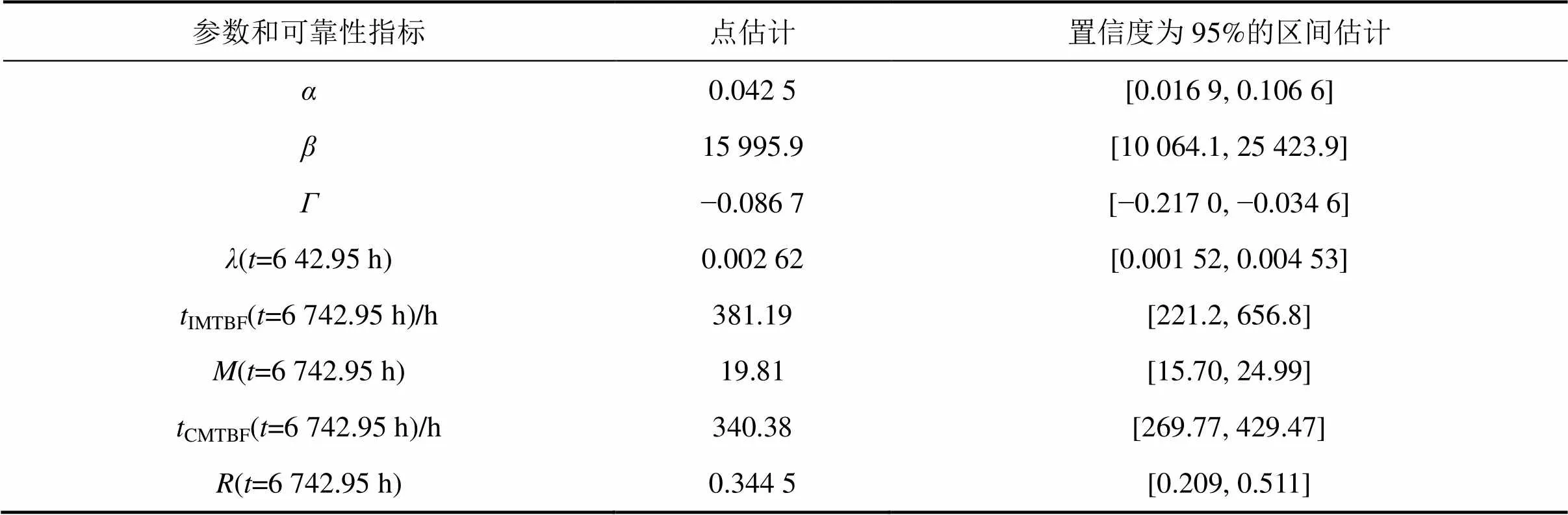
表2 模型参数和可靠性指标的点估计和区间估计
5 结论
1) 本文提出的连续比例强度模型,同时考虑了运行时间及维修行为对系统可靠性的影响,是一种新的不完全维修模型。该模型采用连续函数形式表达,模型参数和可靠性指标具有封闭形式的解,容易获得相应的置信区间,更易于实现工程实际中的可修系统可靠性评估。
2) 利用数控机床现场故障数据对模型进行验证,结果表明,本文模型可以很好地应用于工程实际,为可靠性预测及准确地确定维修策略提供了一定的理论依据。
参考文献:
[1] 王智明, 杨建国. 可靠性模型自助参数估计法[J]. 哈尔滨工业大学学报, 2010, 42(5): 820−823. WANG Zhiming, YANG Jianguo. Bootstrap method of parameter estimation in reliability model [J]. Journal of Harbin Institute of Technology, 2010, 42(5): 820−823.
[2] 谷东伟, 申桂香, 张英芝, 等. 数控机床主轴系统可靠性评价[J]. 中南大学学报(自然科学版), 2013, 44(2): 540−545.GU Dongwei, SHEN Guixiang, ZHANG Yingzhi, et al. Reliability evaluation of spindle system of CNC[J]. Journal of Central South University (Science and Technology), 2013, 44(2): 540−545.
[3] 王智明, 杨建国, 王国强, 等. 多台数控机床最小维修的可靠性评估[J]. 哈尔滨工业大学学报, 2011, 43(7): 127−130. WANG Zhiming, YANG Jianguo, WANG Guoqiang, et al. Reliability assessment of multiple NC machine tools with minimal repair[J]. Journal of Harbin Institute of Technology, 2011, 43(7): 127−130.
[4] Syamsundar A, Naikan V N A. Imperfect repair proportional intensity models for maintained systems[J]. IEEE Transactions on Reliability, 2011, 60(4): 782−787.
[5] Kijima M, Sumita N. A useful generalization of renewal theory: Counting process governed by non-negative Markovian increments[J]. Appl Prob, 1986, 23: 71−88.
[6] Cox D R. The statistical analysis of dependencies in point process[C] // Lewis P A W. Stochastic Point Processes. New York: Wiley-Interscience, 1972: 55−66.
[7] Kaminskiy M, Krvtsov V. A Monte Carlo approach to repairable system reliability analysis[C]// Mosleh A. Probabilistic Safety Assessment and Management. New York: Springer, 1998: 1063−1068.
[8] Doyen L. Asymptotic properties of imperfect repair models and estimation of repair efficiency[J].Nav Res Logist, 2010, 57: 296−307.
[9] Gasmi S. Estimating parameters of a log-linear intensity for a repairable system[J]. Applied Mathematical Modelling, 2013, 37(6): 4325−4336.
[10] Gasmi S. Parameter estimation in an alternating repair model[J]. Journal of Statistical Planning and Inference, 2011,141(11): 3605−3616.
[11] Wang Z M, Yang J G. Numerical method for Weibull generalized renewal process and its applications in reliability analysis of NC machine tools[J]. Computers & Industrial Engineering, 2012, 63: 1128−1134.
[12] Lawless J F, Thiagarajah K. A point-process model incorporating renewals and time trends, with application to repairable systems[J]. Technimetrics, 1996, 38(2): 131−138.
[13] GUO Huairui, LIAO Haitao, ZHAO Wenbiao, et al. A new stochastic model for systems under general repairs[J]. IEEE Transactions on Reliability, 2007, 56(1): 40−49.
[14] GUO Huairui, LIAO Haitao, ZHAO Wenbiao, et al. Practical methods for modeling repairable systems with time trends and repair effects[C]// Reliability and Maintainability Symposium, California: IEEE, 2006: 182−188.
[15] 王智明, 杨建国. 数控机床可靠性评估中的边界强度过程[J]. 上海交通大学学报, 2012, 30(10): 1622−1626. WANG Zhiming, YANG Jianguo. Bounded intensity process and its applications in reliability assessment of NC machine tools[J]. Journal of Shanghai Jiaotong University, 2012, 30(10): 1622−1626.
[16] Sangun P, Balakrishnan N, ZHENG Gang. Fisher information in hybrid censored data[J]. Statistics and Probability Letters, 2008, 78: 2781−2786.
[17] CHEN Xiaoming. Using Akaike information criterion for selecting the field distribution in a reverberation chamber[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55(4): 664−670.
[18] 任丽娜, 芮执元, 李建华, 等. 三参数边界强度过程及其在数控机床可靠性评估中的应用[J]. 西安交通大学学报, 2014, 48(5): 107−112. REN Lina, RUI Zhiyuan, LI Jianhua, et al. Three-parameter bounded intensity process model and its application in reliability assessment of NC machine tools[J]. Journal of Xi’an Jiaotong University, 2014, 48(5): 107−112.
Imperfect repair continuous proportional intensity model for repairable systems and its application
REN Lina1, RUI Zhiyuan1, WANG Zhiming2
(1. School of Mechanical and Electronic Engineering, Lanzhou University of Technology, Lanzhou 730050, China;2. School of Mechanical Engineering, Huaihai Institute of Technology, Lianyungang 222005, China)
Considering that traditional imperfect repair model was difficult to use in practice, a new continuous proportional intensity model with closed-form solutions was proposed based on the theory of bounded intensity process. The characteristics of the model were discussed, the formula of point maximum likelihood estimators for model parameters, as well as the important reliability indices such as the conditional reliability at given time, the s-expected number of failures, and the cumulative mean time between failure were all derived, the interval estimators of model parameters and reliability indices were given by using the Fisher information matrix method and delta method, and the assessment criterion of model was provided based on Akaike information criterion and the index of goodness-of-fit test. An example of real failure data from numerical control machine tools was taken to prove the proposed method. The results show that the closed-form solutions and confidence bounds of reliability indices for NC machine tools are obtained and the method can be well applied in practical.
imperfect repair; continuous proportional intensity model; bounded intensity process (BIP); maximum likelihood estimation; repairable systems
10.11817/j.issn.1672-7207.2015.07.012
TG659;TB114
A
1672−7207(2015)07−2467−07
2014−07−25;
2014−10−04
国家自然科学基金资助项目(51165018);甘肃省省青年科技基金资助项目(145RJYA307) (Project(51165018) supported by the National Natural Science Foundation of China; Project (145RJYA307) supported by the Youth Science and Technology Foundation of Gansu Province, China)
芮执元,教授,博士生导师,从事复杂成套装备数字化设计与制造、系统仿真技术与可靠性研究;E-mail: zhiy_rui@163.com
(编辑 杨幼平)

