基于有限元计算结果的强夯加固效果估算方法

吕先华， 王琨， 邓通发， 罗嗣海

(江西理工大学建筑与测绘工程学院，江西 赣州341000)

基于有限元计算结果的强夯加固效果估算方法

吕先华， 王琨， 邓通发， 罗嗣海

(江西理工大学建筑与测绘工程学院，江西 赣州341000)

为验证和简化已有的强夯效果估算的数值计算结果，运用数据拟合方法对已有无粘性土强夯有限元计算得出的有关图表和曲线关系进行了拟合，得出了便于应用的相关方程和系数表达式，进而提出了应用有限元计算结果估算无粘性土强夯加固效果的步骤.介绍了已有粘性土强夯有限元计算结果和拟合方程.分别用工程实例对无粘性土和粘性土拟合方程进行了验证，验算结果表明，计算结果与实测结果较为吻合，方法为夯前定量预估强夯加固效果随深度的变化提供了一种实用途径.

强夯;有限元;数据拟合;加固效果

0 引 言

强夯的设计方法及加固效果评估，特别是如何依据夯前土质参数和强夯工艺参数估算夯后地基性状及其随深度变化，是一个仍未较好解决需进一步研究的课题[1-6].

由于强夯过程的复杂性，许多学者进行了强夯的数值分析，但多数研究者只关注强夯的动力响应过程，而更有实践意义的是将强夯过程与夯后地基的性状即强夯加固效果联系起来.F.H.Lee，Q.Gu[7]对砂土进行了二维有限元分析，利用离心模型成果对模型进行了验证，对不同强夯工艺参数和土质参数进行了广泛计算，并对计算结果进行了归一化处理，提出了考虑土质和强夯工艺参数的用于估算砂土地基强夯效果的图表.K.F.Mostafa，Robert Y. Liang[8]采用剑桥本构模型和ABAQUS有限元程序对粘性土强夯进行了数值分析，得出了有效加固深度及加固程度等值线与冲击能量及土质参数的相关方程.

但F.H.Lee，Q.Gu[7]计算得出的图表应用较为烦琐，两种土性中有限元成果的实践应用也有待进一步验证.本文分别简要介绍F.H.Lee，Q.Gu[7]无粘性土与K.F.Mostafa，Robert Y.Liang[8]粘性土有限元计算结果，对F.H.Lee，Q.Gu[7]无粘性土图表曲线进行数据拟合，得出相关方程和相关系数表达式，便于工程应用.分别用2个无粘性土和粘性土工程实例的计算与实测结果进行对比，对拟合方程进行验证，探讨成果在工程实践中的可用性.

1 无粘性土强夯有限元计算结果的拟合及其在加固效果估算中的应用与验证

Gu[9]提出了一个干砂上强夯计算模型，应用此强夯分析模型计算得到的加固范围为一灯泡形，其大小可以用某一加固程度的最大加固深度和加固半径来表征，F.H.Lee，Q.Gu[7]对强夯过程中不同土质参数和强夯工艺参数进行了大量的计算，建立了一些基本的理论和公式.

1.1 相对加固程度概念

F.H.Lee，Q.Gu[7]模拟强夯过程，在不同的砂类土中进行试验，根据分析结果对不同初始相对密度的砂进行强夯试验，分析得出初始相对密度对深部加固效果有较大的影响，定义相对密度的相对加固程度Ir:

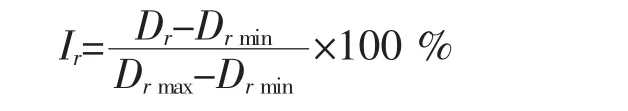
其中:Drmin为夯后最小相对密度，Drmax为夯后最大相对密度.

又考虑到夯后最小相对密度和最大相对密度在强夯之前不容易确定，近似的取为Dr0和100%，则可的近似定义式:

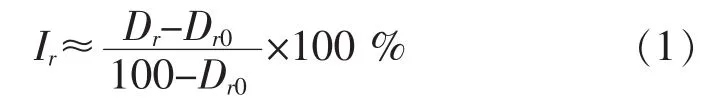
其中:Dr0为初始相对密度.

按式(1)定义分析得出，用相对加固程度来定义时，不同土类和初始相对密度的加固效果随深度变化规律近于相同.

1.2 有限元计算结果及其拟合

1.2.1 单击动量与动能的影响

F.H.Lee，Q.Gu[7]对夯击的能量和动量的影响进行了研究，做了大量的不同能量和不同动量的强夯试验，整理得出了相关图表资料并对数据进行了归一化处理.

1)对不同的能量和动量进行试验，以能量和动量相同时作为参考算例(单击动量能量相等，分别等于200、400和800为参考算例，动量单位为 t· m/s，能量单位为 t·m).对加固深度和单击能量进行归一化处理，得出能量归一化加固深度δE与归一化能量ψ关系，如图1所示.

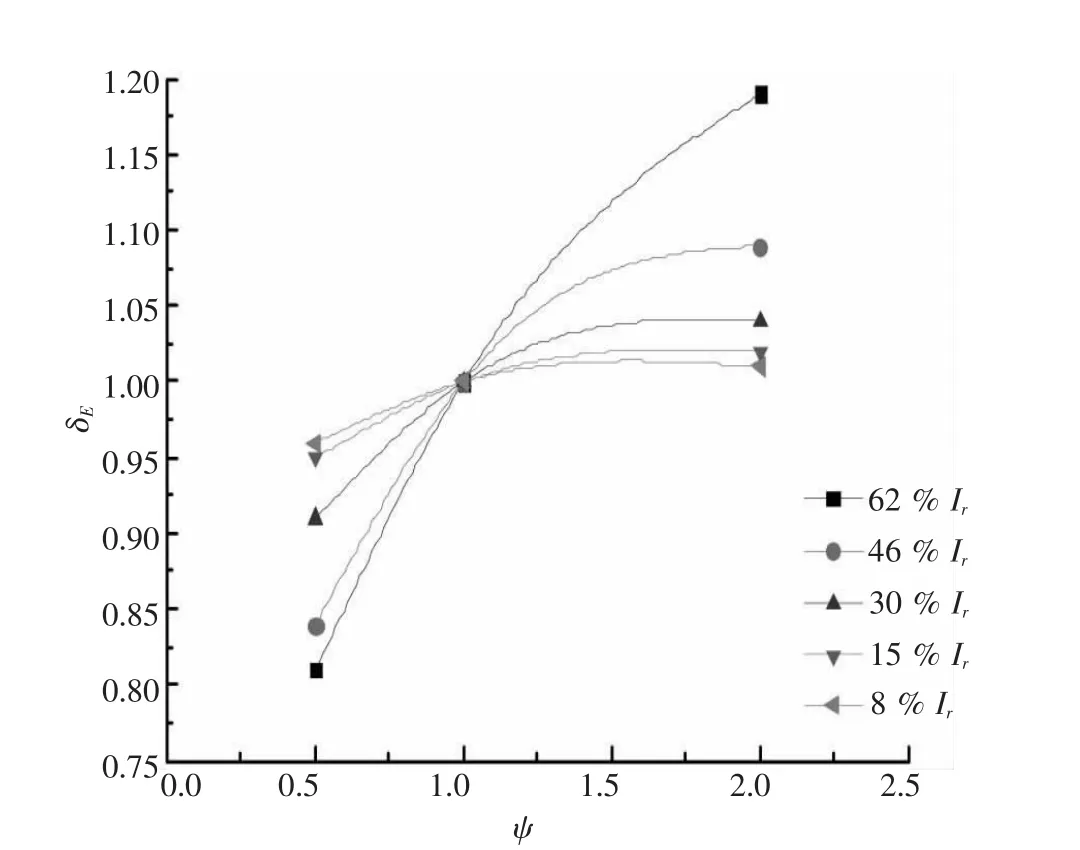
图1 能量归一化加固深度δE与归一化能量ψ关系曲线

对图1曲线进行拟合，得出拟合方程式:

对应各Ir的系数A、B1、B2可由下式计算:

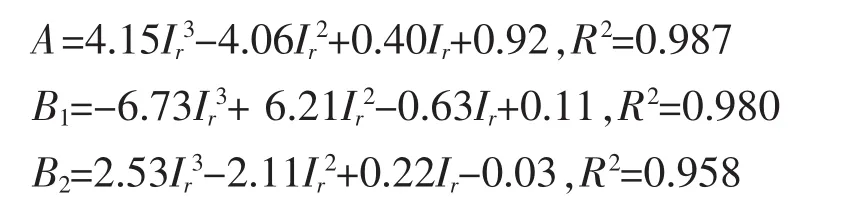
2)参考算例中的加固深度Zr与能量(动量)值是相关的，计单击夯击能量400 t·m和单击夯击动量400 t·m/s时的加固深度为标准加固深度ZS，则3种不同参考算例的加固深度可用ZS来归一化，即归一化加固深度δM=Zr/ZS.

图2可反映动量大小的影响，ZS数值可由图2中查得，也可按下式估算:

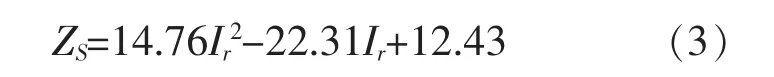
3)考虑归一化加固深度δM与单击动量P之间的关系.不同参考算例中归一化的加固深度δM与动量P(t·m/s)的关系如图3所示.

图2 加固深度与单击动量关系图

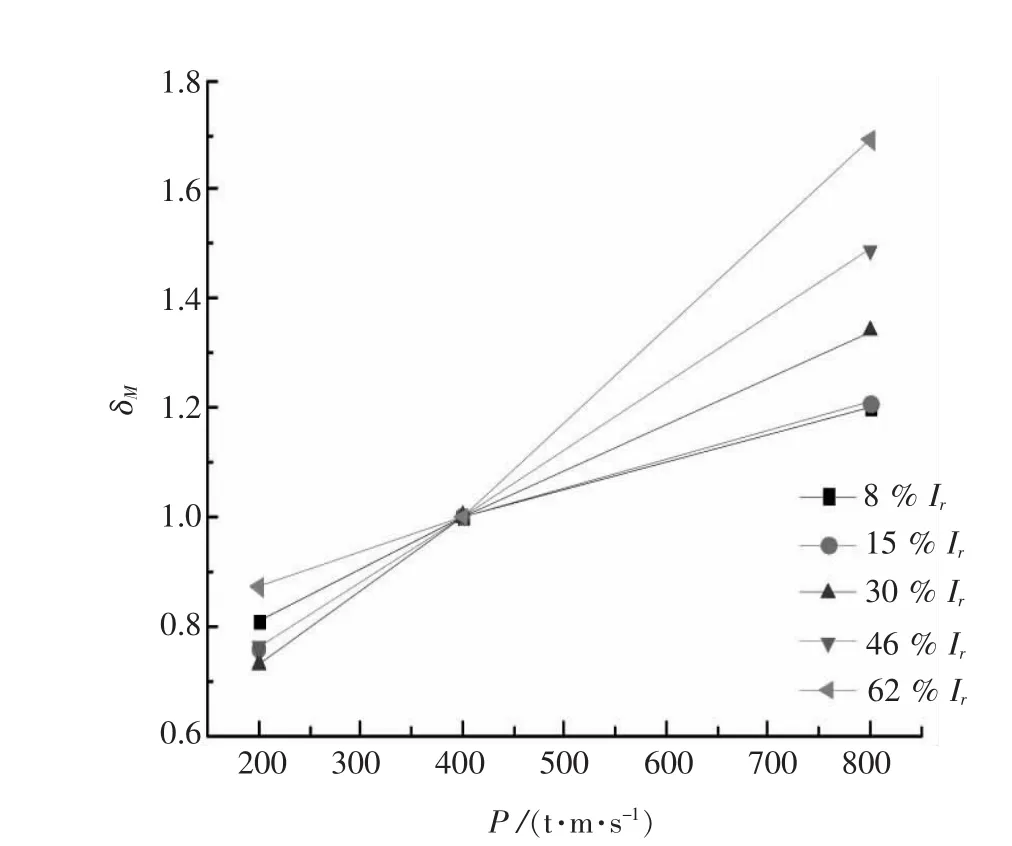
图3 归一化加固深度与单击动量的关系

结合图3，拟合方程为:

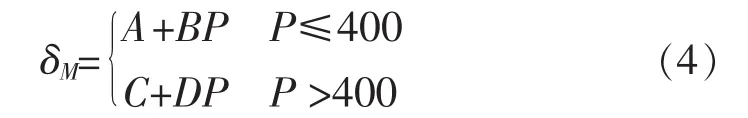
对应的系数A、B、C、D由下式计算:

结合以上式(2)、式(4)可得出某一加固程度的归一化加固深度为:

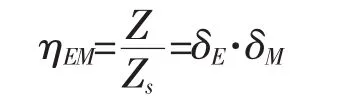
Z为同一动量但能量不同时相应于同一加固程度的深度.只要给定Zs，即可计算出考虑能量和动量的加固深度.

1.2.2 锤底面积的影响

F.H.Lee，Q.Gu[7]通过数值模拟强夯过程，用不同锤底面积进行试验研究，结果表明，某一加固程度的加固深度与锤底面积有关并定义了锤径归一化加固深度，通过对特定的能量和动量进行试验研究，得出了夯锤面积归一化加固深度和夯锤半径的关系，根据其关系分析出对特定的能量和动量存在加固的最优底面积，其半径记为r0.其计算结果如图4所示.

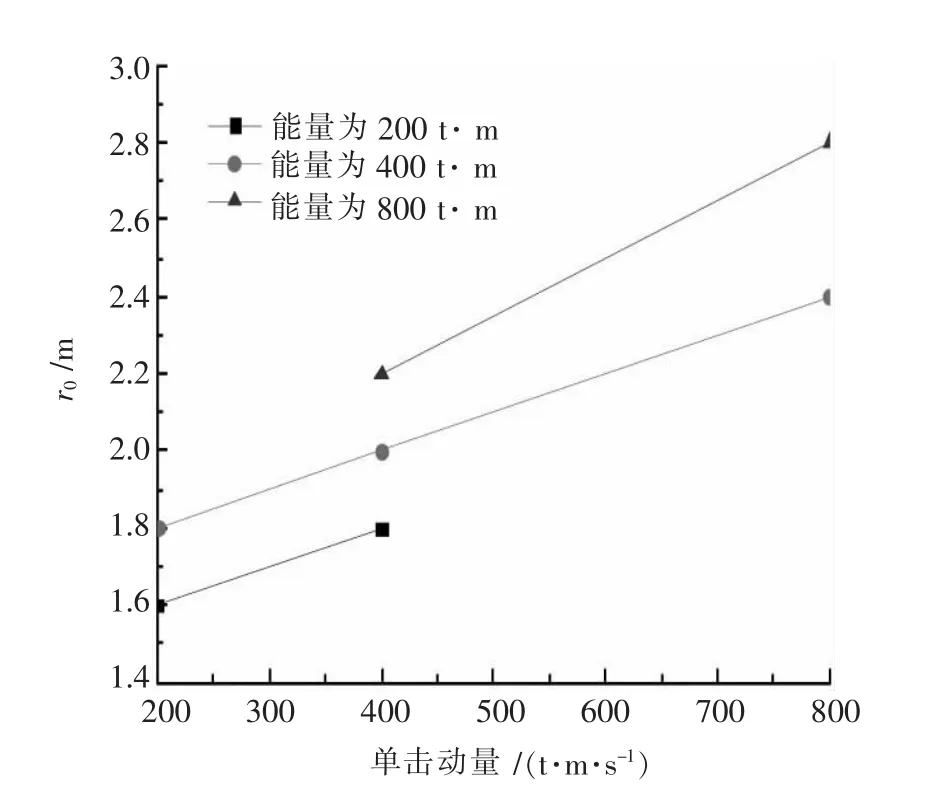
图4 动量和能量对最优半径的影响

将不同情况下的计算结果整理成归一化深度与用最优半径r0归一化的锤径关系，结果如图5所示.

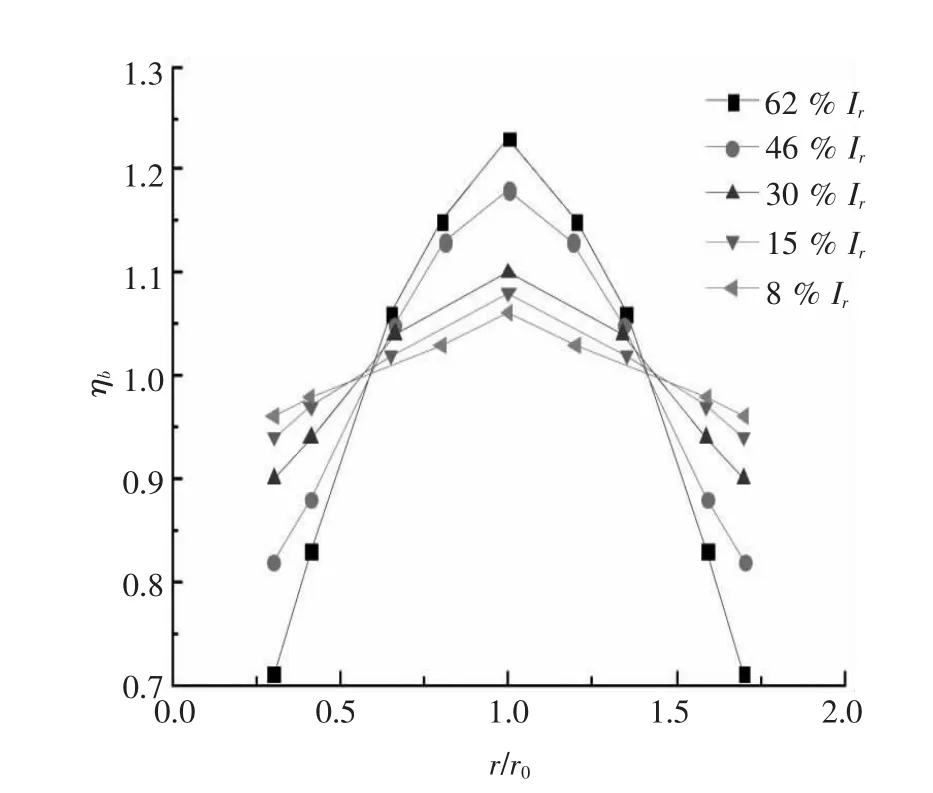
图5 夯锤底面积归一化加固深度ηb与归一化半径r/r0关系曲线

对图5进行数据拟合，得出拟合方程为:

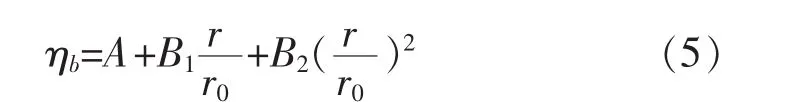
式(5)中系数为:

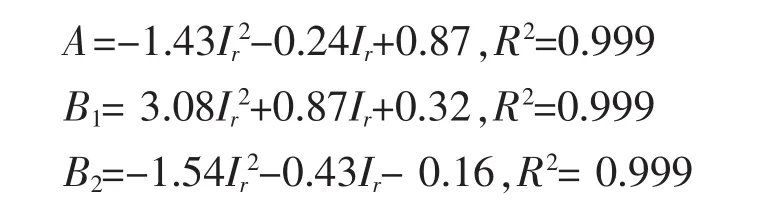
1.3 加固效果的估算方法

基于上面的理论基础，考虑加固效果的各种因素的影响及做的相关归一化处理，建立估算无粘性土强夯加固效果的具体步骤方法:

1)由公式(3)计算对应某一加固程度Ir的标准加固深度Zs(能量为400 t·m，动量为400 t·m/s);计算归一化能量，由公式(2)计算能量归一化深度δE;由公式(4)计算动量归一化参考深度δM，并计算用标准化深度归一化的加固深度ηEM=Z/Zs= δE·δM

2)根据能量和动量从图4中查出最优半径r0(采用内插法)，计算归一化半径r/r0，从公式(5)中计算出锤底面积归一化深度ηb.

3)计算与加固程度Ir相应的加固深度Z=ηEMηbZs

4)计算不同的相对加固程度的深度，可得相对加固程度—深度关系曲线.

5)利用式(1)可进一步计算夯后相对密度—深度关系曲线.

1.4 工程实例计算中的应用与验证

1.4.1 马来西亚Kampung Pakar场地

场地位于距马来西亚Kuala Lumpur-Seremban高速公路附近的Sungei Besi地区[10].一期工程包括在约15英亩土地上修建8个中档五层居住区.在用强夯进行地基处理的c区，土质条件为:14 m以上为松散砂土，其中10～12 m为粉质粘土夹层，14 m以下为灰岩，地下水位埋深约3.0 m.现场试夯时，夯锤重150 kN，锤底面积1.83×1.83 m2(锤径D= 2.05 m)，夯点成6×6 m布置，分三遍夯击，第一遍夯击时落距20 m，夯10击，第二遍夯击时落距25 m，夯6击，第三遍为满夯，落距6 m，夯4击.根据夯击前后测得的锥尖阻力，Y.K.Chow等[11]利用Meyerhof经验方程给出了相对密度剖面，根据1.3节建立的方法计算得出的相对密度剖面及其与由夯后实测锥尖阻力换算出的结果对比如图6所示.

图6 Kampung Pakar场地实测与计算的相对密度剖面

1.4.2 日本Noshiro场地(Tanaka和Sasaki，1989)

场地[10]内表部沉积物主要为7.0 m厚的松散细砂，其下为密实的中—粗砂，夯前地下水位埋深为2.0 m.强夯加固的主要目的是消除松散砂土的液化性.强夯施工采用重W=200 kN、直径D=1.95 m的夯锤，落距25 m.夯点间距6.36 m，梅花形布置，夯击一遍，共35击.夯前、夯后在夯点下测得的典型标贯击数，根据Skempton经验公式，可分别估算夯前和夯后的相对密度.用1.3节的分析方法计算得到的夯后相对密度剖面及其与由实测标贯值换算的结果对比如图7所示.

由图6、图7中两个工程实例验证中可以看出，基于有限元计算结果和拟合方程所建立的无粘性土强夯加固效果估算方法能够较好估算夯后相对密度随深度的变化关系，方法具有一定的实用性.

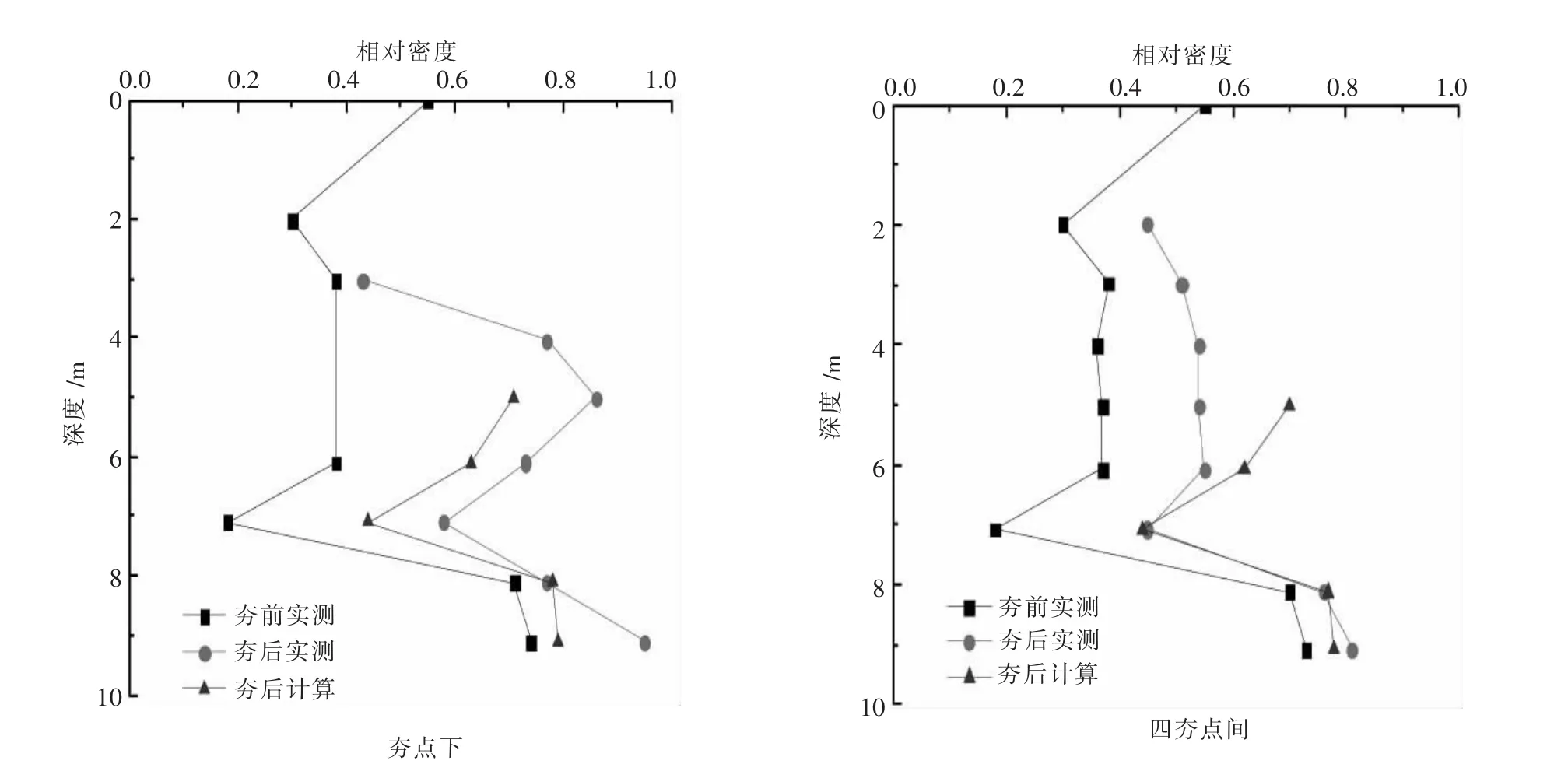
图7 Noshiro场地计算与实测相对密度剖面

2 粘性土强夯有限元计算结果在加固效果估算中的应用与验证

K.F.Mostafa，Robert Y.Liang[8]采用剑桥本构模型和ABAQUS有限元程序对粘性土强夯进行了数值分析，通过计算结果与经验规律和实测结果进行比较，证实程序的可靠性.随后，进行了广泛的参数研究，对结果进行了统计拟合，得出了有效加固深度及加固程度等值线与冲击能量及土质参数的相关方程，可计算出夯坑深度及夯后部分土性指标，可用于粘性土强夯加固效果估算.

2.1 有限元模型与参数取值简介

2.1.1 有限元模型简介

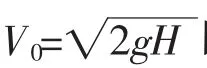
2.1.2 参数取值简介

强夯工艺参数是夯锤半径(r)、夯锤重量(M)和落距(H).表1和表2是用于参数研究的参数范围.分析中相关的剑桥模型参数有6个:p，v，M，eo，λ，ao，其物理含义见表2，弹性体积模量(k)取为0.1λ.

表1 用于参数研究的强夯参数

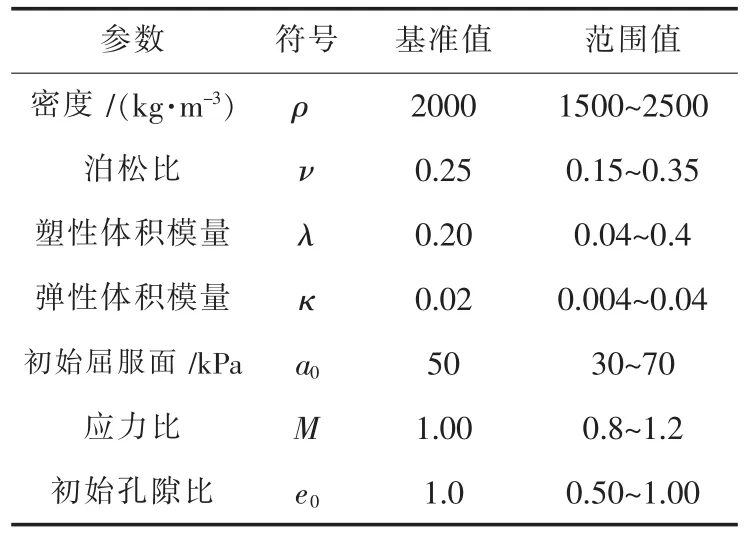
表2 用于有限元参数研究的剑桥模型参数

2.2 计算结果拟合

2.2.1 夯沉量

图8是计算得到的夯坑深度与锤底单位面积夯击动量关系，可见两者大致成线性关系.图9是计算得到的夯坑深度与夯击次数的关系，可见夯坑深度与夯击次数平方根近似成比例增长.图10是归一化夯坑深度与各个土质参数归一化值的关系，随着土性参数的不断改变，夯坑深度也显著变化.

基于图8～图10，将夯坑深度S的估算公式可表达为:

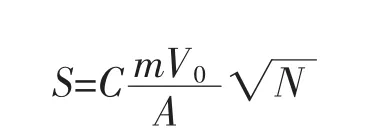
相关系数C取决于土质特性，N为夯击次数.

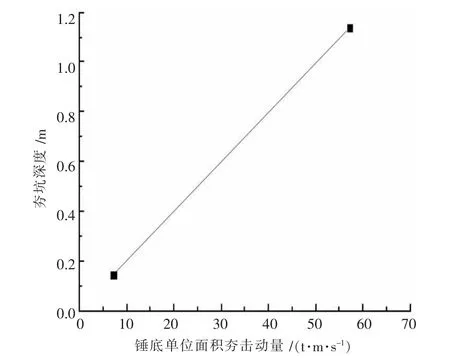
图8 夯坑深度与锤底单位面积夯击动量的关系曲线

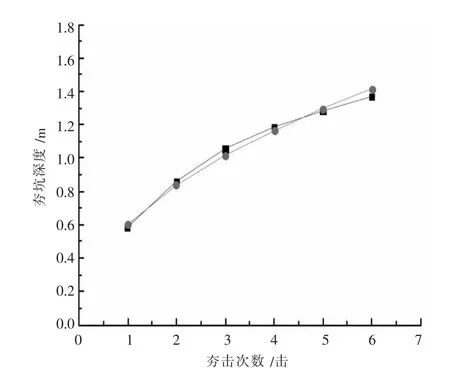
图9 夯坑深度与夯击次数的关系曲线

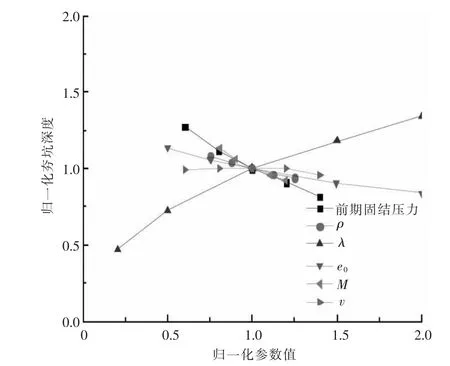
图10 归一化夯坑深度与归一化土质参数的关系曲线

应用统计分析软件SPSS程序对上述结果进行分析，得出相关系数C的如下表达式:

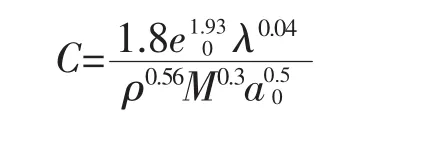
分析得出有限元计算结果和上述公式预测的夯坑深度的较为接近.

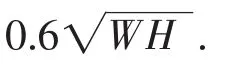
2.2.2 夯后孔隙比估算

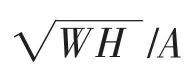
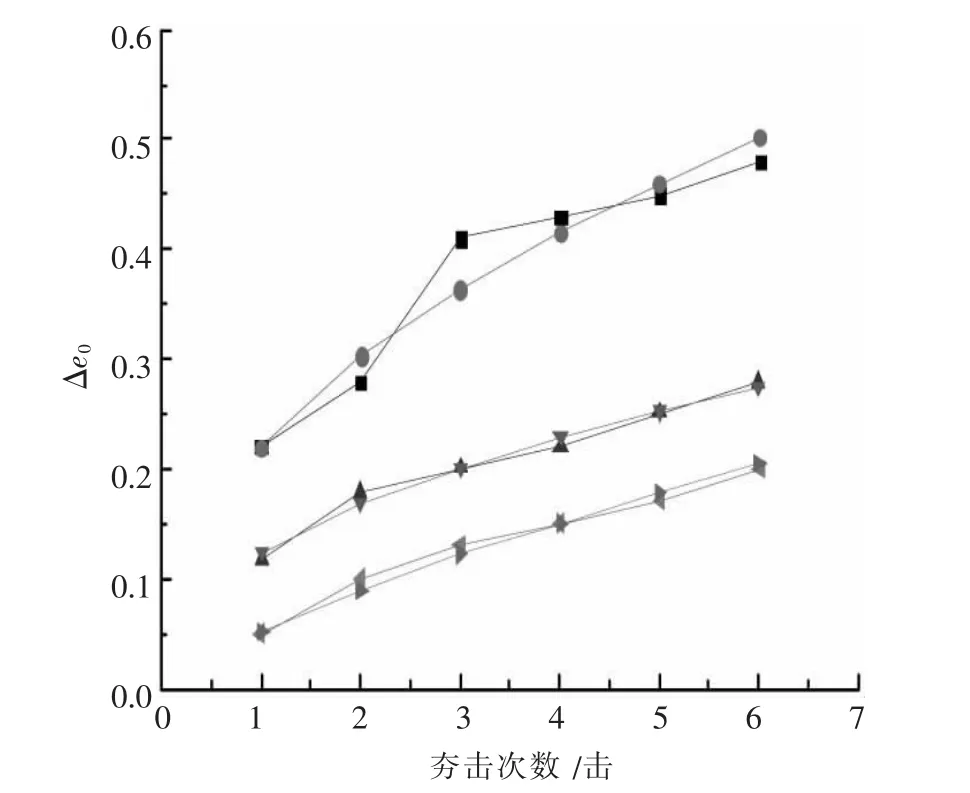
图11 孔隙比减小值随夯击数的变化曲线

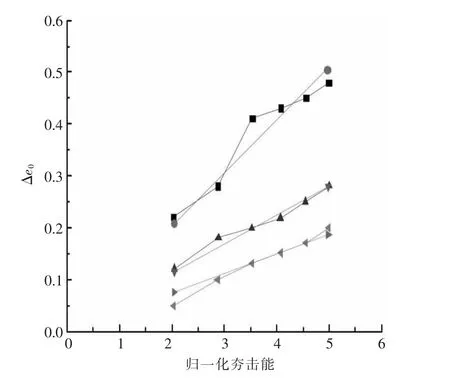
图12 孔隙比减小值随归一化夯击能的变化曲线

基于上述分析，孔隙比减小的估算公式可设为:

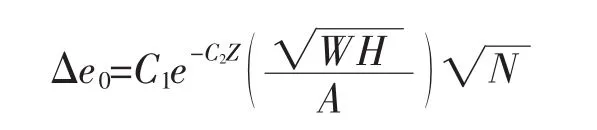
其中:C1和C2是回归参数，与土性参数相关.

利用SPSS统计分析软件，对有限元分析结果进行拟合，可得到C1和C2如下式:

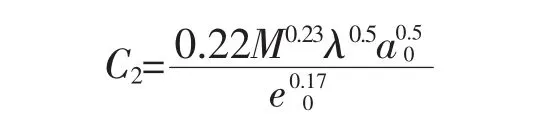
由此可计算夯后孔隙比减小沿深度的变化规律，进而可由e=e0-Δe0计算夯后孔隙比沿深度变化规律.

2.3 工程实例计算中的应用与验证

2.3.1 河北国电龙山电厂

河北国电龙山电厂场地[12]表层主要为粉土，厚度为0.4～2.00 m，结构松散，采用强夯法处理，其中夯击能E为5000 kN·m，夯点间距为3 m，共夯击3遍.夯锤底面积A=4.9 m2，根据剑桥模型中参数的表2以及结合实际土体的初始孔隙比，利用2.2.2节方法，采用表2中剑桥模型参数取值的上限值、下限值、基准值计算的结果与实测值夯击后土体孔隙比随深度的变化如图13所示.

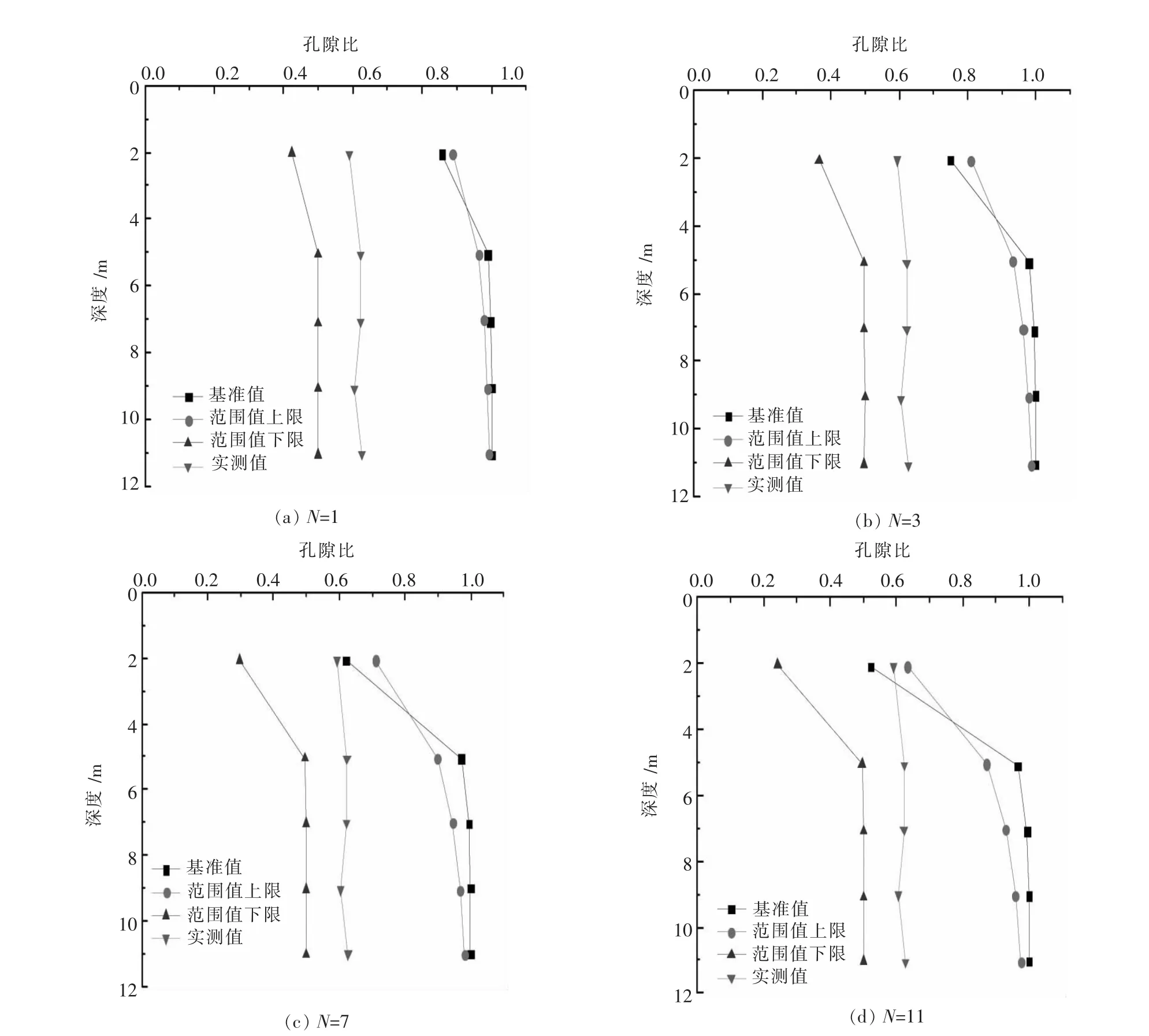
图13 孔隙比随深度变化曲线

从图13中可看出取剑桥模型中的上限范围值得出的结果与实测值较为接近.故确定该实例中计算孔隙比的变化时应用到的剑桥模型参数如表3所示.

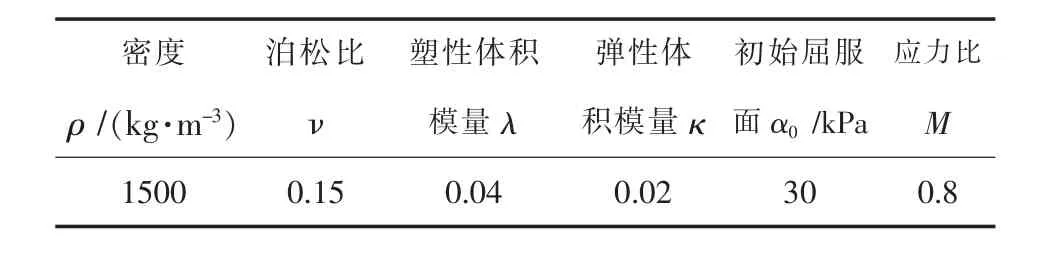
表3 用于实例计算的剑桥模型参数取值

2.3.2 三门峡至灵宝高速

三门峡至灵宝高速公路[13]，该段重粘质黄土及重砂土多，黄土骨架颗粒以粗粉粒为主体，其粒径在0.05～0.01 mm的占60%，不均匀系数Cu在8左右，湿陷系数为0.0150～0.1355，为湿陷性黄土，自重湿陷系数为0.0015～0.088.采用强夯法处理，E=2880 kN·m，A=5 m2，N=12击，在试夯阶段分别采用单击夯击能为2880 kN·m和2250 kN·m两种，锤重18 t，锤径2.5 m，夯点按正方形布置，间距3.2 m，施工分3遍完成.结合夯击前后孔隙比的实际测量值，应用剑桥模型的参数进行计算，图14(a)和(b)分别为夯击能为2250 kN·m时应用表2中剑桥模型参数取值的上限值、下限值、基准值及表3中的参数计算得出的孔隙比随深度的变化和实测值的对比.

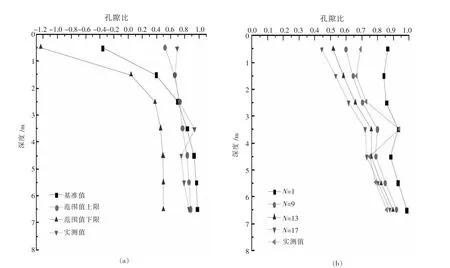
图14 孔隙比随深度变化曲线

从图13、图14中两组实例验证中可以看出，利用2.2.2方法计算夯后孔隙比大小总体上是可行的，但相比之下，利用剑桥模型的上限范围值计算的结果更为理想.

3 结 语

通过计算结果与实测结果对比表明:利用有限元计算结果通过数据拟合得出相关表达式所建立的无粘性土强夯加固效果估算步骤可用于工程实践中;对于有限元计算结果用于估算粘性土强夯加固效果在工程实践中总体是可行的，相比之下，利用剑桥模型的上限范围值计算的结果更为理想.综合表明，基于有限元计算结果的估算方法可作为估算实际工程中强夯加固效果的一种实用途径.

[1]罗嗣海.无粘性土强夯加固效果定量估算的拟静力分析法[J].岩土工程学报，2008，30(4):480-486.

[2]董倩，况龙川，孔凡林.碎石土地基强夯加固效果评价与工程实践[J].岩土工程学报，2011，3(1):330-334.

[3]丁月双，李连营，张学飞.强夯加固深度及加固效果分析[J].施工技术，2012(S2):35-38.

[4]吴立春，王厚星，殷青芳.强夯能量对饱和吹填土地基加固效果的影响[J].工业建筑，2012，42(1):128-132.

[5]吕爽，罗嗣海.砂土强夯加固效果的深度效应[J].江西理工大学学报，2013，34(1):37-41.

[6]宋修广，周志东，杨阳，等.强夯法加固无黏性土路基的现场试验与数值分析[J].公路交通科技，2014，31(3):1-6，37.

[7]Lee F H，Gu Q.Method for estimating dynamic compaction effect on sand[J].JournalofGeotechnicaland Geoenvironmental Engineering，2004，130(2):139-152.

[8]Mostafa K F，Robert Y Liang，Numerical modeling of dynamic compaction in cohesive soils[J].Geo-Frontiers，2011:738-747.

[9]Gu Q.Finite element study of dynamic compaction[D].Singapore: National Univ.of Singapore，2003.

[10]罗嗣海.软弱地基强夯与强夯置换加固效果计算[D].杭州:浙江大学，1999.

[11]Chow Y K，Yong D M.Dynamic compaction of loose sand deposits[J]. Soils and Foundations，1992，32(4):93-106.

[12]任月芬.灰土换填与强夯法在湿陷性黄土地区的应用[J].中国科技信息，2007(16):35-36.

[13]牛希顺，姜永军.三灵高速公路湿陷性黄土路堤基底强夯处理[J].铁道工程学报，2001(4):34-37.

Estimation method of soil improvement effect based on finite element calculation results

LV Xianhua，WANG Kun，DENG Tongfa，LUO Sihai
(School of Architectural and Surveying&Mapping Engineering，Jiangxi University of Science and Technology，Ganzhou 341000，China)

To verify and simplify the numerical calculation results of the existing compaction effects estimation，use the data fitting method to fit related charts and curves of the existing compaction finite element calculations of cohesionless soil with the result of drawing relative and effective equation and coefficients expression and then putting forward the steps of applying finite element calculation results to estimate cohesionless soil consolidation effect.Introduce the existing dynamic finite element calculation results of cohesive soil and its fitting equation.The two kinds of fitting ones are verified respectively with engineering examples with the results that the calculated results agree well with experimental ones.These methods provide a practical way for the prediction of reinforcement effect change with depth before dynamic compaction.

dynamic compaction;finite element;data fitting;reinforcement effect

2095-3046(2015)01-0049-08

10.13265/j.cnki.jxlgdxxb.2015.01.009

TU44

A

2014-08-27

江西省交通厅科技资助项目(2012C0003)

吕先华(1990- )，男，硕士研究生，主要从事岩土工程等方面的研究，E-mail:lvxh2013@163.com.

罗嗣海(1966- )，男，博士后，教授，主要从事岩土力学与地基处理等方面的研究，E-mail:drsoil@163.com.