山区斜坡段桥梁基桩屈曲稳定性分析

宁夏元，尹平保，赵衡



山区斜坡段桥梁基桩屈曲稳定性分析

宁夏元1，尹平保2，赵衡3

(1. 湖南省交通科学研究院，湖南长沙，410015；2. 长沙理工大学土木与建筑学院，湖南长沙，410114；3. 中南大学资源与安全工程学院，湖南长沙，410083)

根据山区斜坡段桥梁基桩的承载机理，考虑桩前岩土体弱化效应，建立斜坡段桥梁基桩屈曲稳定性分析简化计算模型；建立山区斜坡段桥梁基桩桩−坡体系的总势能方程，并利用能量原理及变分法进行求解，导出基桩屈曲临界荷载及稳定计算长度公式；然后，通过与模型试验结果进行对比分析，验证理论解答的可行性；结合有限元法探讨桩身弹性模量、自由段长度、桩径以及嵌固深度等因素对某实体工程桩稳定性的影响。研究结果表明：基桩存在一临界嵌固深度；桩径及埋入比对基桩稳定性影响较大；弹性模量对基桩稳定性影响较小。

桥梁工程；基桩；斜坡；能量法；屈曲

随着越来越多的公路或铁路在西部山区修建，某些路段往往采用高架桥来穿越斜坡或峡谷，从而不得不将基桩设置在陡峭的山坡或岸坡上，这时基桩的稳定性非常突出，应引起高度重视[1−2]。有关桥梁基桩的稳定性问题，国外早有不少学者对其开展过一些有益的研究工作。Reddy等[3]采用能量法对完全和部分入土桩进行了稳定性分析。Poulos等[4]利用弹性理论法、Bowles等[5]利用有限元法对基桩的屈曲稳定性进行了求解。而在胡人礼在20世纪70年代提出基于法的基桩稳定计算长度经验公式；其后，赵明华[6]基于最小势能原理和变分法导出了9种边界条件下基桩屈曲临界荷载及稳定计算长度的能量法解答；Lin等[7]研究了多层地基中基桩的稳定性问题；郭红雨等[8]基于弹性理论，导出了冻土区基桩稳定分析的能量法解答；赵明华等[9]引入突变理论和能量原理，对高桥墩桩基进行了理论研究，得到了高桥墩桩基体系的失稳荷载及对应的墩顶位移；姚文娟等[10]同样基于突变理论和能量法对超长桩的前、后屈曲问题进行了深入研究。然而，上述研究对象均是位于平地上的基桩，而针对山区斜坡段桥梁基桩稳定性方面的研究则鲜有报道。鉴于山区斜坡段桥梁基桩稳定性问题的重要性，应对其展开深入、系统的研究。为此，本文作者在已有研究的基础上[11−13]，根据山区斜坡段桥梁基桩的竖向荷载传递机理及承载特性，考虑桩前岩土体水平地基抗力弱化效应，建立山区斜坡段桥梁基桩稳定性分析简化计算模型及总势能函数，并借助能量原理及变分法进行求解，导出基桩屈曲临界荷载及稳定计算长度计算公式。以此为基础，结合有限元法进一步探讨桩身弹性模量、自由段长度、桩径以及嵌固深度等因素对某实体工程桩屈曲稳定性的影响。

1 计算模型及基本假定

根据基桩与斜坡之间的位置关系，可将基桩分为3段：位于坡面以上的自由段(3)、坡面以下一定深度范围内的抗力弱化段(2)以及进入稳定持力层的嵌固段(1)，由此可以建立如图1所示的山区斜坡段桥梁基桩稳定性分析简化计算模型。图1中：桩顶竖向荷载为；基桩总长123；2tan；为抗力弱化影响范围系数，一般取3~5；为入土段桩径；为边坡坡度；11为基桩入土段抗弯刚度；22为基桩自由段抗弯刚度。

为便于后续分析，首先进行如下基本假定[14]：

1) 假定基桩仅在平面内发生运动，即不考虑基桩在空间上的弯扭或转动，据此可将其转化为一平面问题，并取其最不利平面进行分析，假定坐标原点位于桩端，如图1所示。

图1 基桩屈曲稳定性分析简化计算模型

2) 已有研究表明桩身自重及桩侧摩阻力对基桩屈曲稳定性的影响极小[6]，因此，在建立总势能方程时可忽略二者的影响。

3) 斜坡的存在将导致坡面以下2深度范围内桩侧岩土体水平抗力弱化，须进行合理折减。此时，基于法的桩侧岩土体水平抗力表达式为

式中：(，)为桩侧岩土体水平抗力；为水平抗力折减系数，其取值见文献[2]；1为基桩有效计算宽度；为桩侧岩土体水平抗力比例系数；为桩身挠曲位移；设=1+2，=(2+1)。

4) 不考虑桩顶水平荷载及偏心弯矩的作用。

5) 根据文献[6]桥梁基桩的桩端及桩顶边界条件可分为自由、弹性嵌固、嵌固及铰接等几种。对于山区桥梁基桩，大多数情况下其桩端已嵌入稳定的岩层当中，故假定桩端嵌固更为合理；对于桩顶则可选取自由和弹性嵌固2种不利情况进行稳定性分析，其对应的桩身挠曲函数如下：

对于桩端嵌固、桩顶弹性嵌固，

对于桩端嵌固、桩顶自由，

式中：c为待定系数；为基桩总长；为半波数。

2 能量法解答

2.1 总势能方程的建立

根据图1所示的简化计算模型，并基于上述基本假定，即可建立山区斜坡段桥梁基桩桩−坡体系的总势能方程。桩−坡体系的总势能由桩身应变能P、桩侧岩土体弹性应变能s及桩顶荷载势能P组成，即

桩身应变能P为

桩侧岩土体弹性应变能s为

桩顶外荷载势能P为

将式(5)~(7)代入式(4)可得

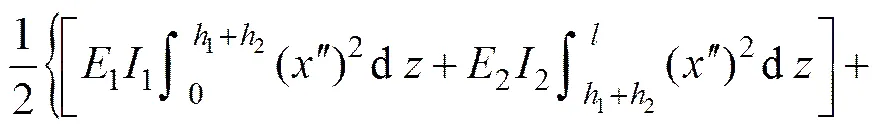
2.2 能量法解答

可以利用能量法对方程式(8)进行求解。限于篇幅，这里仅以桩端嵌固、桩顶自由为例，对方程式(8)进行求解。首先将式(3)及其一、二阶导数代入式(8)，然后根据势能驻值原理，对其取变分，并令，即

将式(9)展开，可得

式中：A，A，B，B，C，C，D，D，E，E，F，F，G，G，J，J，k和k均为与，，，，和(=1，2，…，)和(=1，2，…，)等有关的系数。

式(11)为一齐次线性方程组，其矩阵形式为

式(12)中总共有个变量c(=1，2，3，…，)，要使其具有非零解，则其系数行列式必为0，即

式(13)即为山区斜坡段桥梁基桩屈曲稳定性分析的特征方程。对式(13)进行求解，并设其最小正根为min，则可得到基桩的屈曲临界荷载cr：

则对应的基桩稳定计算长度P为

3 试验验证

为验证本文计算方法及程序的可靠性，现以文献[13]中的试验桩为例进行对比验证。理论计算时半波数取50（一般来说，宜取大于20的整数），其他参数与文献[13]中的相同。该模型试验桩的边界条件为：1~6号桩桩端嵌固、桩顶自由；7~12号桩桩端嵌固、桩顶弹性嵌固。模型试验桩为木桩，桩周填土为型砂。该试验的基本参数及计算结果如表1和表2所示。

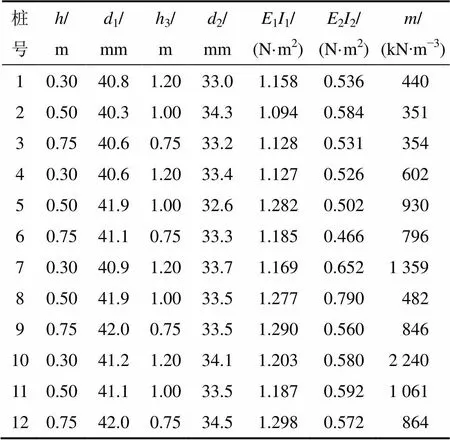
表1 试桩计算参数

注：，1和11分别为入土段基桩桩长、桩径及抗弯刚度；3，2和22分别为自由段基桩长度、桩径及抗弯刚度。

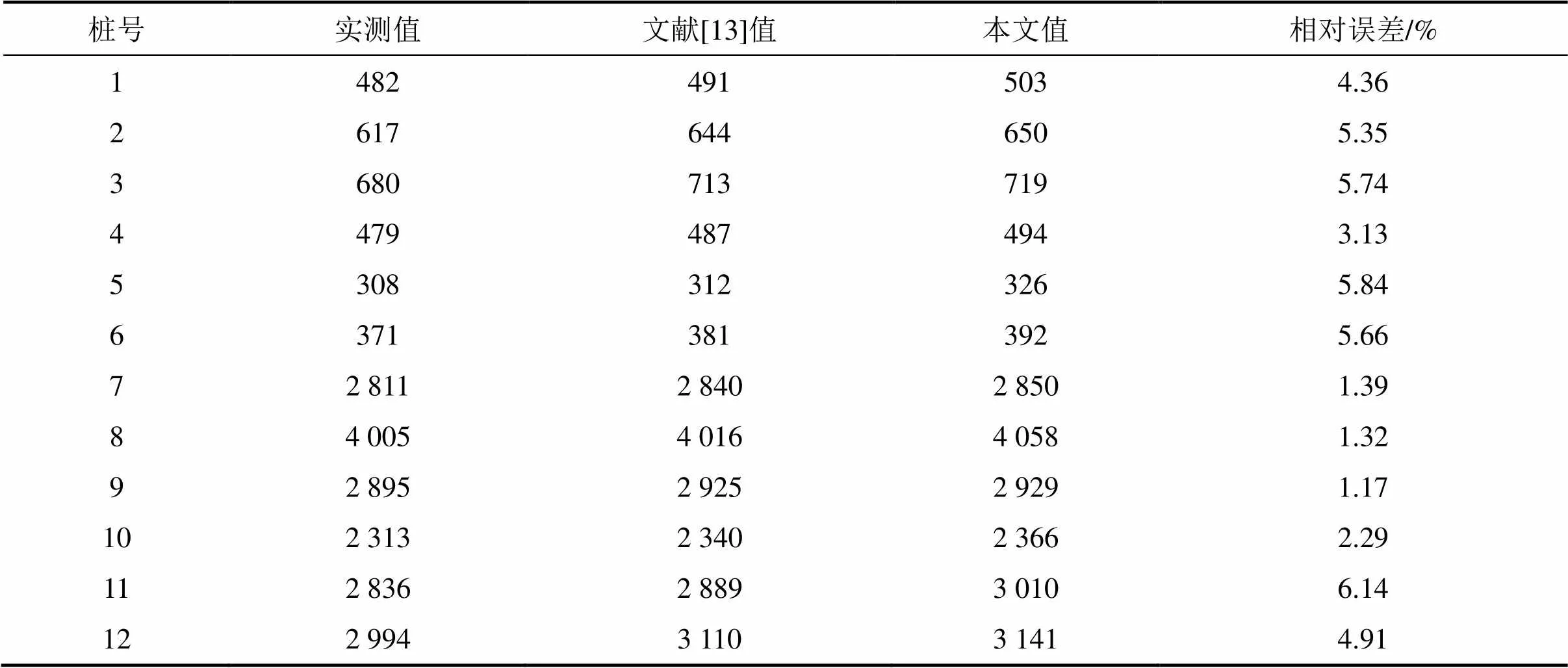
表2 临界荷载计算结果对比

由表2可以看出，本文计算结果与实测结果及文献[13]中计算结果均比较接近，本文计算值与实测值的最大计算误差尚低于10%，说明本文计算方法是可行的。

4 工程实例分析

现以张(张家界)—花(花垣)高速公路某斜坡段桥梁基桩为例，利用本文计算方法及有限元法对其屈曲稳定性进行理论及数值模拟分析。以探讨自由段长度3、桩身弹性模量、桩径及嵌固深度1对其屈曲稳定性的影响。该桥梁基桩的主要计算参数为：基桩自由段长3=8.0 m；基桩入土段长=25.0 m。自由段直径2=1.8 m，入土段基桩直径1=2.0 m。自由段采用C30混凝土，其弹性模量为30 GPa；入土段基桩采用C25混凝土，其弹性模量为28 GPa，取水平抗力比例系数当量为77 952 kN/m4。

4.1 数值分析模型及计算参数

根据该基桩的实际工程资料，采用ADINA数值计算软件，进行数值模拟计算。建模时，桩体弹性本构模型及桩侧岩土体均服从摩尔−库仑强度准则，根据最不利状况，设桩顶边界条件为自由。

单位：mm

表3 数值分析计算参数

注：为弹性模量；为泊松比；为黏聚力；为内摩擦角；为重度。

4.2 计算结果分析

应用ADINA后处理模块获得了竖向荷载作用下基桩屈曲稳定性计算结果，图3所示为桩顶竖向荷载作用下桩−坡体系的变形图。为了显示桩−坡体系的相对变形特性，将变形图进行放大处理，放大倍数为1.5×105。另外，从图3可以看出：计算得到的临界荷载因子约为6.68×108，即基桩的屈曲临界荷载cr为682 MN，其与利用本文理论计算方法得到的结果715 MN基本吻合。

图3 桩−坡体系变形图

4.3 影响因素分析

为探讨桩身弹性模量对陡坡段桥梁基桩屈曲稳定性的影响，保持其他参数不变，选取0.5，1.0和1.5分别利用能量法和有限元法进行计算分析，从而得到不同桩身弹性模量下，基桩屈曲临界荷载cr与自由段长度之间的关系曲线如图4所示。

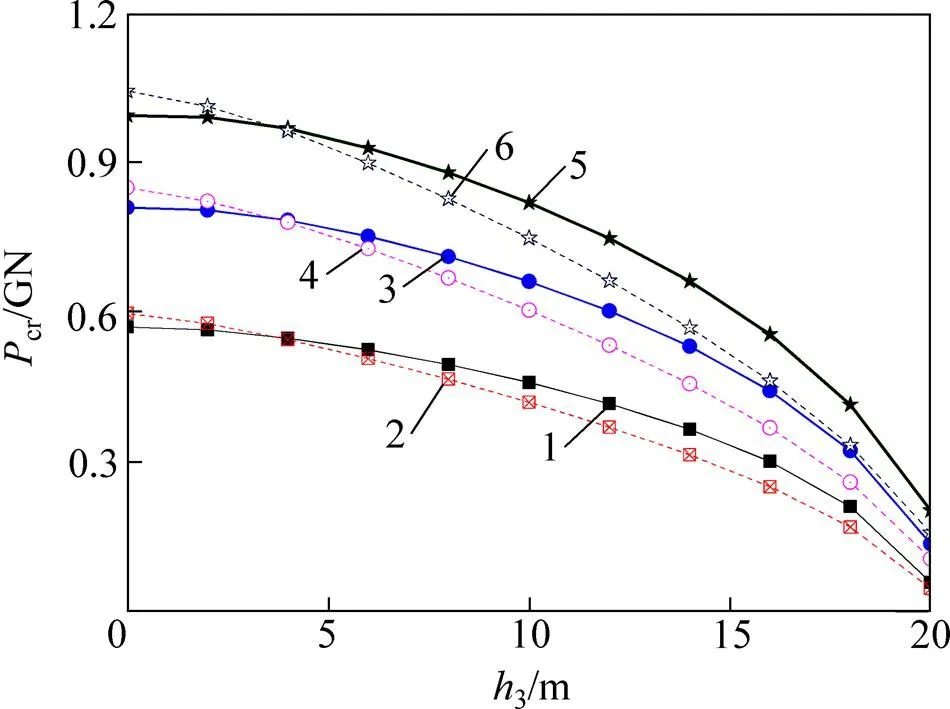
1—0.5E(能量法)；2—0.5E(有限元法)；3—1.0E(能量法)；4—1.0E(有限元法)；5—1.5E(能量法)；6—1.5E(有限元法)

图5所示为不同弹性模量下临界荷载cr与嵌固段长度1的关系曲线。由图4和5可知：桩身弹性模量越大，基桩的屈曲临界荷载cr也就越大；当桩身弹性模量由0.5增大到1.5时，基桩的屈曲临界荷载值提高了1.5~2.0倍；随基桩自由段长度3的增加，临界荷载cr逐渐减小；而随着嵌固段长度1的增加，基桩屈曲临界荷载cr逐渐增大；但当嵌固段长度增大到18 m左右时，嵌固段长度1与基桩屈曲临界荷载cr的关系曲线趋于平缓，即继续增加嵌固段长度对改善基桩的屈曲稳定性已不明显，此嵌固深度即为基桩稳定的临界嵌固深度。

1—0.5(能量法)；2—0.5(有限元法)；3—1.0(能量法)；4—1.0(有限元法)；5—1.5(能量法)；6—1.5(有限元法)

图5 不同弹性模量下临界荷载cr与嵌固段长度1的关系曲线

Fig. 51−crrelationship curve under different elastic modulus

对比图4和5可以发现：减小基桩的自由段长度和增加其嵌固深度，均可提高基桩的屈曲稳定性。因此，设计时，应根据工程的实际情况，选取1个合理的埋入比（基桩入土深度与总长之比），确保基桩的最佳稳定性。

图6所示为不同桩径下临界荷载cr与自由段长度3的关系曲线。由图6可以看出：当桩径由1(即2 m)增大到2(即4 m)时，基桩的屈曲临界荷载提高了5~6倍。由此可见：与提高桩身混凝土强度相比，增大桩径对改善其稳定性更有效。

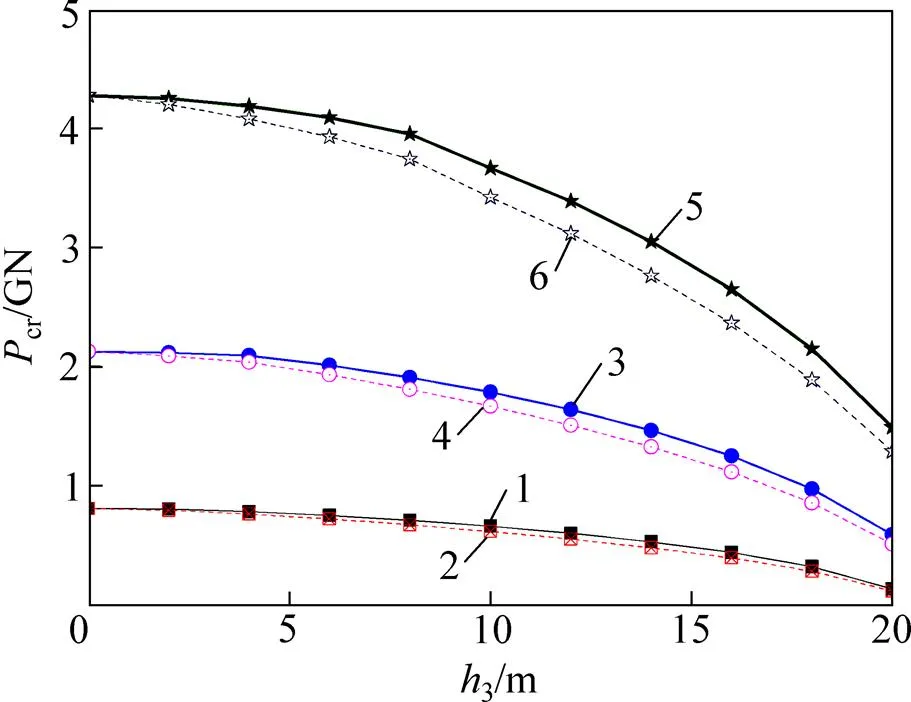
1—0.5E(能量法)；2—0.5E(有限元法)；3—1.0E(能量法)；4—1.0E(有限元法)；5—1.5E(能量法)；6—1.5E(有限元法)

5 结论

1) 分析山区斜坡段桥梁基桩的竖向承载机理，并基于一些假定，建立山区斜坡段桥梁基桩屈曲稳定性分析简化计算模型；其次，导出了桩−坡体系的总势能方程，并利用能量法对其进行求解，获得了斜坡段桥梁基桩屈曲临界荷载及稳定计算长度公式；以某模型试验桩为例，通过理论与实测结果的对比分析，验证了理论计算方法的可行性。

2) 在上述理论研究的基础上，以某实际工程为例，借助ADINA有限元软件，建立相应的数值计算模型，分析了桩−坡体系的变形及基桩的屈曲稳定性，再次验证了理论方法的合理性。进而通过理论与数值计算，探讨了基桩自由段长度3、桩身弹性模量、桩径及嵌固深度1对其屈曲稳定性的影响。

3) 考虑基桩稳定性时，往往存在一临界嵌固深度(18 m)；选择合理的埋入比可使基桩保持最优的稳定状态(可取0.6)；与提高桩身混凝土强度相比，增大桩径对改善其稳定性更有效。

[1] 冯忠居. 特殊地区基础工程[M]. 北京: 人民交通出版社, 2008: 163−164. FENG Zhongju. Foundation engineering in special area[M]. Beijing: China Communication Press, 2008: 163−164.

[2] 赵明华, 尹平保, 杨明辉, 等. 高陡斜坡上桥梁桩基受力特性及影响因素分析[J]. 中南大学学报(自然科学版), 2012, 43(7): 2733−2739. ZHAO Minghua, YIN Pingbao, YANG Minghui, et al. The analysis of influence factors and mechanical characteristics of bridge piles in high and steep slopes[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2733−2739.

[3] Reddy A S, Valsangkar A J. Buckling of fully and partially embedded piles[J]. Journal of Soil Mechanics and Foundation Divison, ASCE, 1970, 96(6): 1951−1965.

[4] Poulos H G. Davis E H. Pile foundation analysis and design[M]. New York: John Wiley and Sons Inc, 1980: 325−335.

[5] Bowles J E. 基础工程分析与设计[M]. 唐念慈, 译. 北京: 中国建筑工业版社, 1987: 1−9. Bowles J E. Foundation Analysis and Design[M]. TANG Lianzi, trans. Beijing: China Building Industry Press, 1987: 1−9.

[6] 赵明华. 桥梁桩基的屈曲分析及试验[J]. 中国公路学报, 1990, 3(4): 47−56. ZHAO Minghua. Pile foundation analysis and experimental buckling[J]. China Journal of Highway and Transport, 1990, 3(4): 47−56.

[7] Lin S S, Chang W K. Bucking of piles in a layered elastic medium[J]. Journal of the Chinese Institute of Engineering, 2002, 25(2): 157−169.

[8] 郭红雨, 贾艳敏. 用能量法确定考虑冻胀力和冻土抗力作用时桩基的临界荷载[J]. 工程力学, 2007, 24(7): 167−173.GUO Hongyu, JIA Yanmin. Determination of critical loads for piles by energy method considering frost heave forces and resistance to deformation of frozen soil[J]. Engineering Mechanics, 2007, 24(7): 167−173.

[9] 赵明华, 蒋冲, 曹文贵. 高桥墩-桩基结构体系屈曲的突变理论分析[J]. 中国公路学报, 2008, 21(2): 49−53. ZHAO Minghua, JIANG Chong, CAO Wengui. Catastrophe theory analysis of structural system buckling of high bridge pier and pile foundation[J]. China Journal of Highway and Transport, 2008, 21(2): 49−53.

[10] 姚文娟, 傅祥卿, 仇元忠. 超长桩的屈曲荷载计算[J]. 地下空间与工程学报, 2009, 5(3): 463−467.YAO Wenjuan, FU Xiangqin, QIU Yuanzhong. Buckling loads for super-long piles[J]. Chinese Journal of Underground Space and Engineering, 2009, 5(3): 463−467.

[11] 赵明华, 王杜鹃, 杨明辉. 高墩−群桩体系临界荷载计算[J]. 湖南大学学报(自然科学版), 2011, 38(8): 1−6. ZHAO Minghua, WANG Dujuan, YANG Minghui. Critical load calculation of high−pier and pile groups system[J]. Journal of Hunan University (Natural Sciences), 2011, 38(8): 1−6.

[12] 朱媛媛, 胡育佳, 程昌钧. 非线性弹性土中桩基的屈曲和后屈曲分析[J]. 力学季刊, 2012, 33(4): 526-534.ZHU Yuanyuan, HU Yujia, CHENG Changjun. Analysis of buckling and post-buckling for piles in non-linear elastic soils[J]. Chinese Quarterly of Mechanics, 2012, 33(4): 526−534.

[13] 汪优. 高桥墩桩基稳定性分析及其优化设计研究[D]. 长沙: 湖南大学土木工程学院, 2007: 81−97. WANG You. Buckling analysis and optimization design for piles foundation with high bridge piers[D]. Changsha: Hunan University. College of Civil Engineering, 2007: 81−97.

[14] 赵明华, 刘恩, 汪优. 桩柱式高桥墩桩基稳定性分析[J]. 公路交通科技, 2008, 25(7): 95−99. ZHAO Minghua, LIU En, WANG You. Stability analysis of pile foundation with higher pile-column bridge piers[J]. Journal of Highway and Transportation Research and Development, 2008, 25(7): 95−99.

Buckling analysis of bridge piles in mountain slopes

NING Xiayuan1, YIN Pingbao2, ZHAO Heng3

(1. Hunan Communications Research Institute, Changsha 410015, China;2. School of Civil Engineering and Architecture,Changsha University of Science and Technology, Changsha 410114, China;3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

By considering the mechanical response of piles and the weakening effect of soil in front of piles, a calculation method was proposed for buckling analysis of bridge piles in slopes. Total potential energy equation of the pile-soil system was established, where buckling critical load and stability calculation length were derived by using energy method. Compared with model test results, the feasibility of the proposed method was verified. In addition, the parametric studies were conducted by FEM, such as elastic modulus, diameter, free length, and embedded depth of piles. The results show that diameter and embedded ratio are closely related to quality of the stability, but little related with elastic modulus conversely.

bridge engineering; pile; slope; energy method; buckling

10.11817/j.issn.1672-7207.2015.10.027

TU352

A

1672−7207(2015)10−3752−06

2015−02−27；

2015−05−22

国家自然科学基金资助项目(51408066，51478051)(Projects (51408066, 51478051) supported by the National Natural Science Foundation of China)

宁夏元，高级工程师，硕士生导师，从事公路桥梁工程等相关研究；E-mail：pingbaby921@163.com

(编辑 陈爱华)