一种新型的注入式混合有源电力滤波器直接功率控制方法
舒大松,黄挚雄,杨仁利,周要
一种新型的注入式混合有源电力滤波器直接功率控制方法
舒大松1, 2,黄挚雄1,杨仁利1,周要1
(1. 中南大学信息科学与工程学院,湖南长沙,410083;2. 湖南广播电视大学机电工程系,湖南长沙,410004)
基于注入式混合有源电力滤波器(injection type hybrid active power filter, IHAPF)因存在基波谐振支路,使得有源部分不承受基波电压,适用于高电压、大容量配电网谐波治理的特点,对注入式混合有源电力滤波器基本结构和工作原理进行分析,论述注入式混合有源电力滤波器采用直接功率控制的可行性;根据瞬时功率理论,将检测出来的谐波功率作为参考信号,使滤波器实际输出的谐波功率跟踪参考功率,从而达到谐波治理的效果。对系统参数进行设计,以保证系统安全可靠运行。研究结果表明:该方法省去了谐波电流检测和复杂坐标变换,提高系统动态控制性能;所采用的直接功率控制在IHAPF谐波补偿中是可行的。
注入式有源电力滤波器;直接功率控制;瞬时功率理论;谐波电流
现代电力电子设备大量使用对电网等造成严重谐波污染[1],具有补偿特性好、抑制能力强和动态响应迅速的有源电力滤波器成为谐波治理的主要方式。随着技术进步,开关管器件容量[2]增加,使得有源电力滤波器容量能够满足低压场合要求,但在中高压大容量系统中,传统的串、并联结构有源电力滤波器难以满足谐波抑制要求。注入式混合有源电力滤波器由于注入支路作用,使用基波电压只作用于注入支路,而有源部分仅承受谐波电压,所以具有满足中高压系统下提供无功补偿和谐波抑制能力[3−5]。目前,人们对注入式APF(active power filter)的研究主要基于电流控制策略[6−8]。检测负载电流控制策略主要是检测出负载谐波电流,然后向电网注入等量的谐波电流,以达到补偿的目的,但这种控制方法不能抑制无源滤波器与电网串、并联谐振问题。检测电网电流控制能更好地减小谐波含量,但会引起系统不稳定,而且不快速。近年来,直接功率控制(direct power control, DPC)因具有控制简单、动态性能良好等优点而被大量应用于有源电力滤波器。乐江源等[9−10]从不同角度将直接功率控制应用于APF系统,提高了APF的动态性能、系统稳定性、谐波抑制能力等。与电流控制相比,采用直接功率控制对系统模型要求不高,控制结构简单,无需复杂坐标变换与计算,具有更高的功率因数。但以上研究都是基于并联性有源电力滤波器,并没有对注入式混合有源电力滤波器直接功率控制进行研究。为此,本文作者首先阐述注入混合有源电力滤波器系统结构、工作原理,建立IHAPF数学模型。在此基础上提出直接功率控制策略,采用电压外环和功率控制内环,通过基于瞬时功率理论,将检测负载谐波功率作为参考信号,与有源电力滤波器输出功率进行比较得到期望值,通过滞环比较器得到开关表输入值,产生PWM信号驱动开关管,使有源电力滤波器输出与谐波功率大小相等、方向相差的180°谐波有功功率和无功功率,以实现IHAPF快速功率调节和谐波抑制。
1 IHAPF系统结构
注入式混合有源电力滤波器系统由电压源型逆变器、输出滤波器、耦合逆变器、基波串联谐振支路、注入支路、无源滤波器和非线性负载组成,如图1所示。图1中:s为电网电压;s为电网电感;0为输出滤波器电感;f和f分别为谐振支路电容和电感;G为注入电容;s,L,Z,C和R分别为电网电流、负载电流、注入电流、补偿电流和谐振支路电流。f和f构成串联谐振在基波频率时阻抗很小,电网电压集中在G,而有源部分只承受很小的谐波电压,所以大大减小了有源部分的容量。在谐波分量时,f和f构成的网络阻抗随着频率的增高而迅速增大,相当于断路,而G阻抗却随着频率增高而减小,因此,有源部分产生的谐波电流绝大部分都将流入注入支路。注入支流这种拓扑优势使得其适用于高压电力系统。
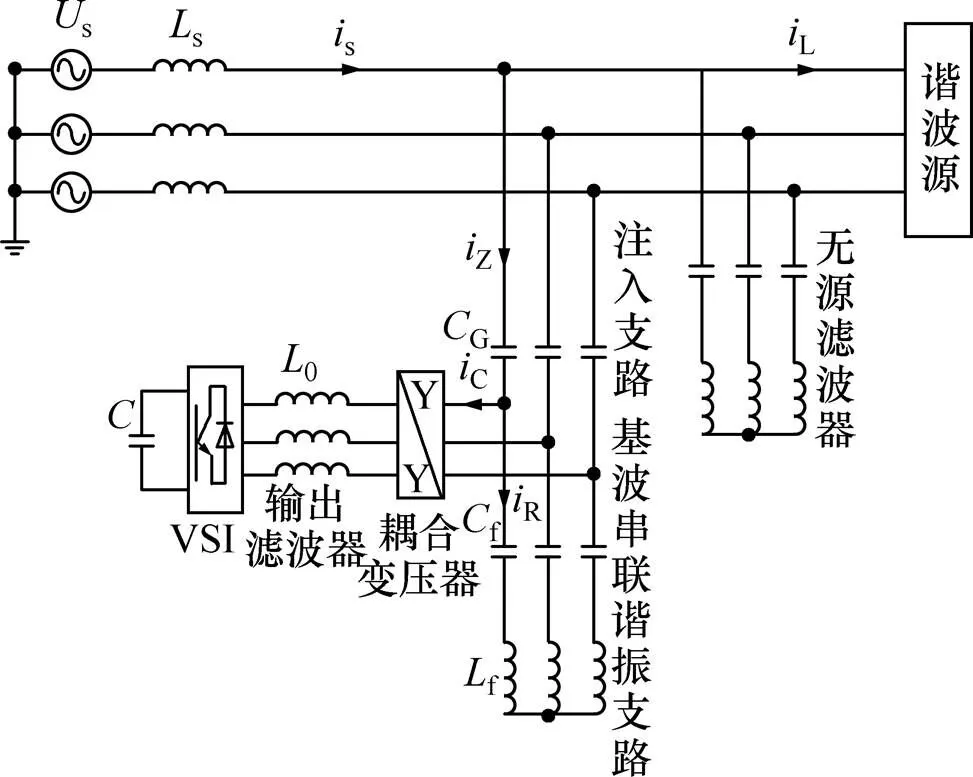
图1 IHAPF系统结构
简化的单相等效电路如图2所示。参照文献[11],为分析方便,电路中无电网电压源和负载谐波电流源,将耦合逆变器等效到输出滤波器边,逆变器等效为1个受控电压源,其输出电压为inv,经耦合变压器等效为inv。根据基尔霍夫电压和电流定律,可以得到逆变器输出电压inv和注入电网谐波电流ch关系。

图2 简化的单相等效电路
由图2可得
其中:
f为基波谐振支路电感内阻;s为电网阻抗;G为注入电容;0和0分别为输出滤波电感内阻和电感量;为复变量。求解式(1),得
得到逆变器输出补偿电流与电压传递函数()为
将式(4)进行如下变换:

对式(5)进行简化,得
式中:f为基波谐振支路阻抗,随着频率升高,f越来越大。式(6)中趋向于0,得
从式(7)可以看出基波谐振支路在高频处对()几乎没有影响。
2 直接功率控制原理
基于直接功率控制的注入式混合有源电力滤波器单相等效原理如图3所示[12],其中,Lh和s分别为负载谐波电流源和电网电压。
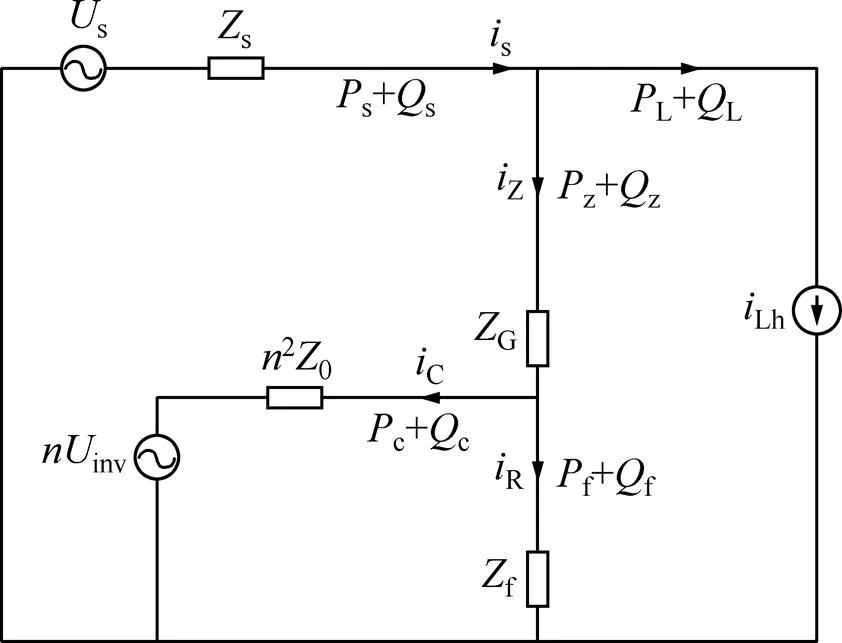
图3 单相等效电路
假设电网电压不含有谐波[13],电网提供的有功功率和无功功率分别为s和s,负载消耗的有功功率和无功功率分别为L和L,有源电力滤波器补偿的有功功率和无功功率分别为c和c,谐振支路有功功率和无功功率分别为f和f,注入支路有功功率和无功功率分别为z和z。根据功率平衡和基尔霍夫电压和电流定律,得
其中:j为虚数。在非线性负载中,L和L都含有由负载侧基波正序电流在基波正序电压作用下的瞬时有功Lf、无功Lf的直流分量和负载谐波电流在基波正序电压作用下的瞬时有功Lh、无功Lh交流分量,所以,
由式(8)和(9)得
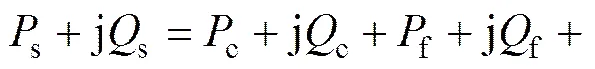
随着谐波频率增加,f和f构成基波谐振支路阻抗迅速增加,相当于断路,所以忽略f和f的影响,式(10)可以简化成
当有源电力滤波器输出满足
时,将式(12)代入式(11),有
通过有源电力滤波器补偿掉负载中含有谐波有功功率和无功功率,这样电网就只含有基波正序电流和基波正序电压作用的有功功率和无功功率。
3 直接功率控制策略
采用直接功率控制注入式混合有源电力滤波器系统结构,如图4所示,该结构由直流侧电压外环和功率控制环组成。通过控制负载谐波有功功率和无功功率等于有源部分补偿的有功和无功功率,功率计算在静止坐标系下求得,实现有功和无功的解耦。

图4 IHAPF 控制策略框图
在两相静止坐标系下,基于瞬时无功功率理论,负载谐波电流有功功率和无功功率检测结果如图5所示。将电网电压sabc通过32变换得到静止坐标系下分量s和s,将负载电流通Labc通过32变换得到静止坐标系下分量L和L,由公式计算负载瞬时有功功率L和瞬时无功功率L,L和L经过低通滤波器(low-pass filter, LPF)得到基波分量,最后将总的瞬时功率减去基波功率得到负载谐波电流瞬时功率交流分量Lh和Lh。
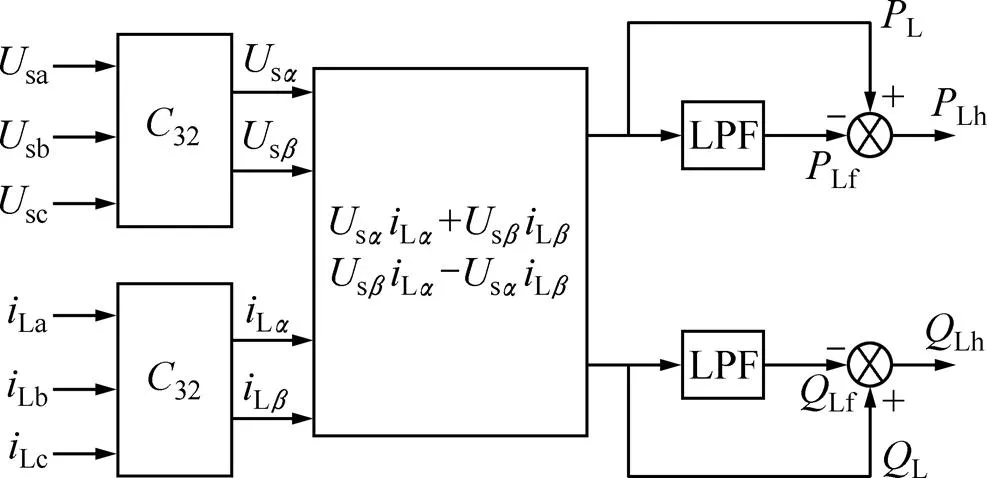
图5 基于p-q理论的谐波电流功率计算结构图
32变换矩阵为。
由瞬时功率理论计算负载瞬时有功功率和无功功率:
根据图6可以得到:
式中:C和C分别为逆变器输出在两相静止坐标系下瞬时有功功率和无功功率;和分别为逆变器输出电流cabc在两相静止坐标系下的分量。
如图4所示,负载谐波有功功率参考值Lh与直流侧输出有功功率dc相加,与实际补偿有功功率c相减作为滞环比较器输入,得到开关信号p。无功功率参考值Lh与实际补偿无功功率C的差值经过滞环比较器后,输出开关信号q。p,q和幅角作为开关矢量表的输入,产生开关驱动信号。p和q满足下式:

其中:p和q为滞环比较器的宽度。
4 仿真结果
无源滤波器参数设计参照文献[1]。由于系统只存在6±1(=1,2,…)次谐波,所以,无源支路设计为11次和13次,根据系统要补偿无功容量,最终选定11=13.7 mH,11=6.7 μF,品质因数=35;13=10.2 mH,13=6.2 μF,=35。
基波谐振支路和注入电容设计参照文献[13],由于5次和7次谐波含量较高,基波谐振支路和注入电容构成1个谐振频率为6次单调谐型无源滤波器,对5次和7次谐波进行抑制,选取f=19.1 mH,f=531 μF,G=15.2 μF。
由系统容量选择耦合变压器变比=2,直流侧电容=10 mF,电压d=900 V,输出滤波器电感取值0=1 mH。
为了验证上述理论的正确性,在MATLAB/Simulink下搭建基于直接功率控制注入式混合有源电力滤波器模型。系统参数为:电网电压s=10 kV,电网额定频率=50 Hz;采用非线性带阻感性负载,=200 Ω,=1 mH;开关频率s=10 kHz。
图7和图8所示为采用直接功率控制IHAPF谐波的补偿效果。其中,图7(a)所示为电网侧电压,不含有谐波成分;图7(b),(c)和(d)所示分别为负载谐波电流、投入PF后电网侧电流和投入APF+PF后电网侧电流。从图7可见:投入PF后,电流谐波有所下降,但还不能达到国家标准,投入APF+PF后,电流谐波含量大幅度下降,波形良好。
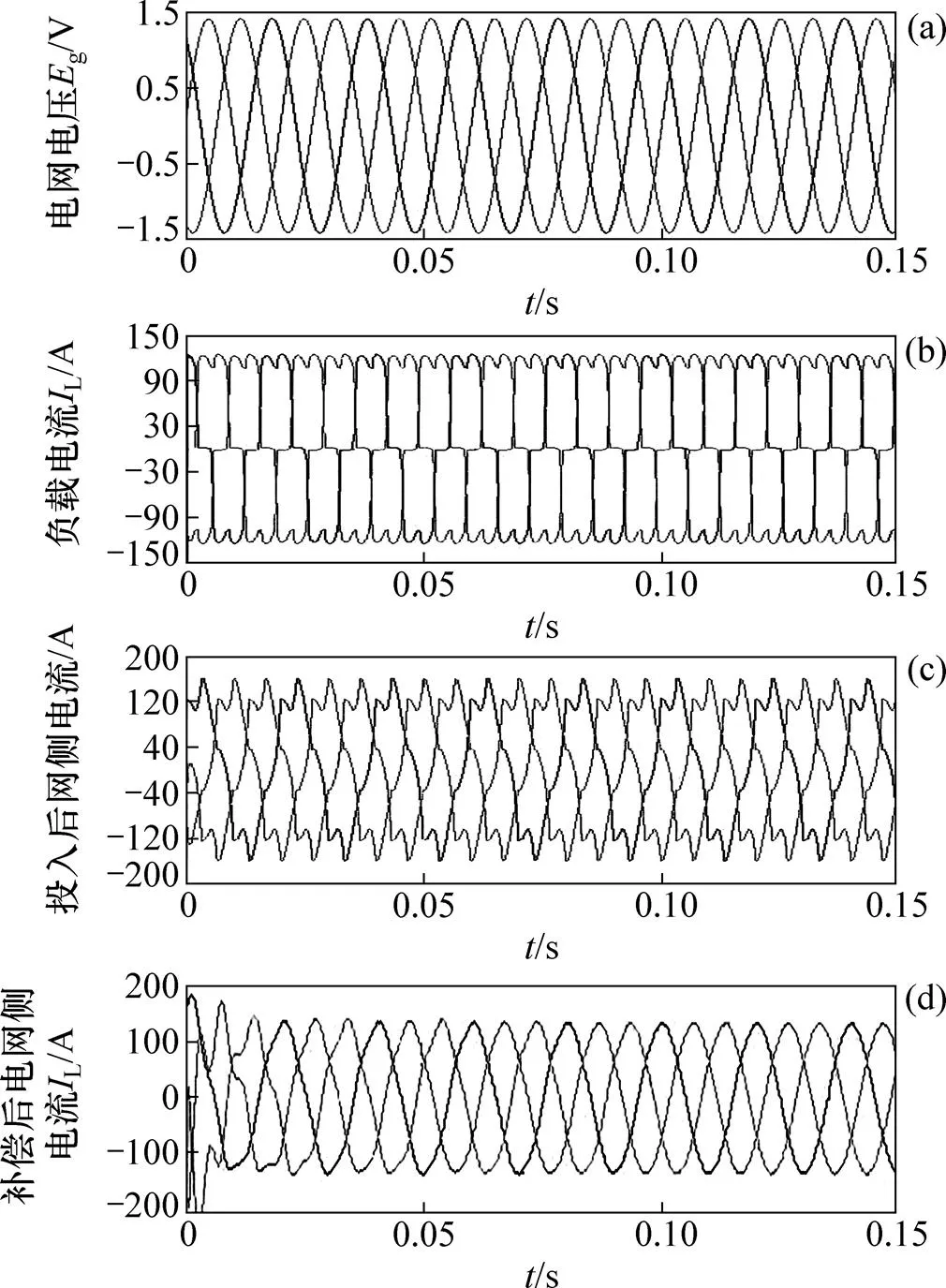
(a) 电网电压;(b) 负载电流;(c) 投入PF后电网侧电流;(d) 投入APF+PF后电网侧电流

(a) 补偿前;(b) 补偿后
从图8可看出:在投入IHAPF之前,电网侧电流谐波总畸变率为26.61%,主要谐波为6±1次;投入IHAPF后,谐波含量大幅度下降,总谐波失真只有1.19%,取得了良好的补偿效果。
直接功率控制下功率波形如图9所示。从图9可以看出:在开始阶段系统的有功功率和无功功率存在一定的波动,但这波动对系统稳定性影响较小。这是因为过了一段时间后,有功功率和无功功率的波动得到了缓解和抑制,但还是存在波动。这主要是因为电网电压较大,与电流的乘积数值很大,造成了有功功率和无功功率波动大。

(a) 有功功率;(b) 无功功率
5 结论
1) 分析了注入式混合有源电力滤波器的结构和工作原理,并对补偿谐波电流与逆变器输出电压之间传递函数进行分析,在高频处忽略基波谐振支路影响。
2) 通过瞬时功率理论对单相等效IHAPF进行研究,证明直接功率控制在IHAPF中应用的可行性。
3) 将直接功率控制应用于注入式混合有源电力滤波器,以瞬时功率作为控制变量,理论分析结果和仿真结果验证了该方法具有动态性能好、系统控制结构简单,只需计算功率,省掉了谐波检测,并能取得良好的谐波补偿效果。
[1] 王兆安, 杨君, 刘进军. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 1998: 15−45.WANG Zhaoan, YANG Jun, LIU Jinjun. Harmonic suppression and reactive power compensation[M]. Beijing: China Machine Press, 1998: 15−45.
[2] 王兆安, 黄俊. 电力电子技术[M]. 北京: 机械工业出版社, 2011: 30−60.WANG Zhaoan, HUANG Jun. Power electronic technology[M]. Beijing: China Machine Press, 2011: 30−60.
[3] 谭甜源, 罗安, 唐欣, 等. 大功率并联混合型有源电力滤波器的研制[J]. 中国电机工程学报, 2004, 24(3): 41−45. TAN Tianyuan, LUO An, TANG Xin, et al. Development of high-capacity hybrid power Filter[J]. Proceeding of the CSEE, 2004, 24(3): 41−45.
[4] 唐欣, 罗安, 涂春鸣. 新型注入式混合有源滤波器的研究[J]. 电工技术学报, 2004, 19(11): 50−55. TANG Xin, LUO An, TU Chunming. Study of new injection type hybrid active power filter[J]. Transactions of China Electrotechnical Society, 2004, 19(11): 50−55.
[5] 夏向阳, 罗安, 周柯. 单独注入式有源电力滤波器的研究与应用[J]. 电力系统自动化, 2005, 29(20): 68−70. XIA Xiangyang, LUO An, ZHOU Ke. Novel active power filter with single injection circuit and its applications[J]. Automation of Electric Power Systems, 2005, 29(20): 68−70.
[6] 汤琛. 串联谐振注入式混合有源电力滤波器研究[D]. 武汉: 华中科技大学电气与电子工程学院, 2006: 20−34. TANG Chen. Research on hybrid active power filter with series resonance injection[D]. Wuhan: Huazhong University of Science and Technology. School of Electrical and Electronic Engineering, 2006: 20−34.
[7] 孙贤大, 罗安, 帅智康, 等. 注入式混合型有源电力滤波器双闭环控制[J]. 电工技术学报, 2009, 24(9): 128−133. SUN Xianda, LUO An, SHUAI Zhikang, et al. Dual-loop control strategy of hybrid active power filter with injection circuit[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 128−133.
[8] 汪玉凤, 王秋保, 赵锐, 等. 串联谐振注入式混合有源电力滤波器的研究[J]. 电力电子技术, 2012, 46(6): 42−44. WANG Yufeng, WANG Qiubao, ZHAO Rui, et al. Research on hybrid active power filter with series resonance injection[J]. Power Electronics, 2012, 46(6): 42−44.
[9] 乐江源, 张志, 赖小华. 三相并联型有源电力滤波器预测直接功率控制[J]. 电机与控制学报, 2012, 16(5): 86−90. LE Jiangyang, ZHANG Zhi, LAI Xiaohua. Predictive direct power control of three-phase shunt active power filter[J]. Electric Machines and Control, 2012, 16(5): 86−90.
[10] 沈玲菲, 危韧勇, 徐保友, 等. 一种新型的有源电力滤波器直接功率控制方法[J]. 电力系统保护与控制, 2013, 41(4): 91−96. SHEN Lingfei, WEI Renyong, XU Baoyou, et al. A novel APF direct power control approach[J]. Power System Protection and Control, 2013, 41(4): 91−96.
[11] 吴传平, 罗安, 帅智康, 等. 注入式混合有源电力滤波器的数学模型及其特性[J]. 中国电机工程学报, 2009, 29(36): 35−41.WU Chuanping, LUO An, SHUAI Zhikang, et al. Mathematical model and characteristics of injection type hybrid active power filter[J]. Proceeding of the CSEE, 2009, 29(36): 35−41.
[12] 李慧, 王奔, 李虎威, 等. 有源电力滤波器双开关表直接功率控制策略研究[J]. 电气传动, 2011, 41(5): 20−24.LI Hui, WANG Ben, LI Huwei, et al. Study of double switching table DPC control strategy for active power filter[J]. Electric Drive, 2011, 41(5): 20−24.
[13] 帅智康, 罗安, 范瑞祥, 等. 注入式混合有源电力滤波器的注入支路设计[J]. 电力系统自动化, 2007, 31(5): 1−5.SHUAI Zhikang, LUO An, FAN Ruixiang, et al. Injection branch design of injection type hybrid active power filter[J]. Automation of Electric Power Systems, 2007, 31(5): 1−5.
A novel IHAPF direct power control method
SHU Dasong1, 2, HUANG Zhixiong1, YANG Renli1, ZHOU Yao1
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China; 2. Department of Mechatronics Engineering, Hunan Radio & TV University, Changsha 410004, China)
Injection type hybrid active power filter is applied in high-voltage and high-capacity power grid harmonic control because its active part is not exposed to the fundamental voltage by the fundamental resonance branch. The basic structure and working principle of injection hybrid active power filter (IHAPF) were analyzed and the feasibility of using direct power control for injection type hybrid active power filter was discussed. According to the instantaneous power theory, harmonic power was detected as the reference signal and the actual harmonic power of filter output would track the reference power to restrain harmonics. To ensure the system is safe and reliable in operation, the system parameters were designed. The results show that the method does not need to detect the harmonic current or transform the complex coordinate, and that the system dynamic control performance is improved. The direct power control is practical in IHAPF harmonic compensation.
injectionactive power filter; direct power control; instantaneous power; harmonic current
10.11817/j.issn.1672-7207.2015.10.016
TM 76
A
1672−7207(2015)10−3670−06
2014−11−12;
2015−01−10
国家自然科学基金资助项目(61203031)(Project (61203031) supported by the National Natural Science Foundation of China)
黄挚雄,博士,教授,从事分布式发电及其控制技术研究;E-mail:zxhuang@csu.edu.cn
(编辑 陈灿华)

