多尺度波形层析反演在高精度速度建模中的应用

马一鸣，孙赞东，唐志远，余立文（.中国石油大学地质地球物理综合研究中心，北京049；.中海油能源发展工程技术分公司，天津300457）

多尺度波形层析反演在高精度速度建模中的应用

马一鸣1，孙赞东1，唐志远2，余立文1
（1.中国石油大学地质地球物理综合研究中心，北京102249；2.中海油能源发展工程技术分公司，天津300457）

波形层析反演方法利用地震波的振幅和相位信息，通过波场重构获得地下参数信息，理论上可以获得更高精度和分辨率的速度模型。但由于受反演算法本身强非线性特征的影响，以及对初始模型依赖程度较高，波形层析反演技术在实际应用中难以取得理想效果。提出一种改进的多尺度反演方法，结合地质层位解释结果，建立较高精度的深度域偏移速度场作为波形层析反演初始输入模型，通过频率域波形层析算法实现多尺度反演降低反演的非线性，并将其成功应用于Marmousi数值模型和某海上实际资料处理。通过将改善后的深度域速度模型应用于Kirchhoff

多尺度；波动方程；波形层析反演；速度建模

随着我国油气勘探的深入，油气勘探的重点正转向复杂构造区和非构造圈闭发育区，对地震成像技术提出了更高的要求和挑战[1]。叠前深度偏移是改善地震资料质量、提高成像精度的有效技术，近年来受到广泛关注。高精度速度模型是做好叠前深度偏移的关键，是获取高信噪比、高分辨率和高保真度地震成像剖面的保证[2]，因此，提高速度模型的精度对于地震勘探意义重大。

传统的速度建模技术包括叠加速度分析、偏移速度分析和射线层析反演等。其中，叠加速度分析简单易于实现，理论成熟，但是，基于水平层状介质的反射波双曲线时距曲线方程，不能适应倾斜地层和速度横向变化的情况。偏移速度分析是利用偏移成像结果来建立速度误差判断准则及速度更新函数，通过修改初始偏移速度模型，获得理想的偏移速度模型。但是在偏移速度分析中，走时和振幅的计算是基于高频近似的假设条件，得到的速度仅包含速度场中的低波数成分，不能对地下岩性构造精确成像[3]。速度层析反演技术主要包括射线层析反演和波形层析反演：射线层析反演技术只利用了相位信息，需要沿反射层拾取旅行时，当信噪比低或者地震波场复杂时，同相轴的识别和拾取十分困难，而且两点射线追踪时要考虑多路径，在中深层速度建模受到限制[4]；波形层析反演方法利用地震全波场信息重构获得地下参数信息，包括波场的走时、振幅和相位信息，无需拾取旅行时，并且不依赖于层位约束，理论上可以获得精度和分辨率更高的速度模型[5-6]。但是，由于受实际地震资料中缺失低频信息以及存在噪声的影响，反演方法具有强非线性特征，对初始模型依赖程度较高，反演结果容易陷入局域小值，使得波形层析反演方法在实际应用中难以取得理想效果[7-8]。针对这些问题，文献［9］引入了多尺度方法对带限地震数据进行反演，针对地震数据中的不同频率成分由低频计算到高频，低频输出的反演结果作为高频输入，降低反演过程的非线性，避免反演结果收敛于局域小值的影响。

基于以上思想，本文提出了一种改进的多尺度反演策略，以波形层析反演为核心，联合层析偏移速度分析（TMVA）进行反演。在初始模型方面，选用叠前偏移速度分析结果，相对常规速度分析，偏移速度分析可以提高道集信噪比，消除绕射波干扰，使反射波归位后速度场位置关系更准确。在算法应用方面，首先，基于Marmousi数值模拟结果验证多尺度波形层析反演算法的有效性；然后，将该反演策略应用于某海上实际地震资料，分别将波形层析反演更新前、后的速度模型应用于叠前深度偏移，通过对比偏移成像结果以及共成像点道集来评价反演速度模型的准确性。

1　基于波形层析反演的速度建模方法

波动方程反演的正确性首先依赖于正演数值模拟的正确性，数值模拟同地震波传播的真实过程越接近，利用初始模型和地震记录的残差数据对模型更新的结果越可信。常用的波动方程正演模拟方法有积分方程法、有限差分法、伪谱法和有限元法。有限差分法求解频率域声波方程的优势在于对阻抗矩阵进行LU三角分解之后，对不同炮点的波场计算过程可以重复使用分解得到的LU矩阵，而反演过程包含大量的正演计算，可提高反演效率。

在频率域，二维声波方程在均匀各向同性介质中传播满足（1）式：

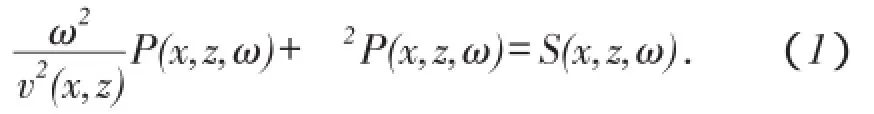
在频率域，声波方程正演可以写成矩阵形式[10]：

（2）式可以通过对稀疏矩阵B的LU分解进行求解。

定义误差向量δd=dobs-dcal，根据最小二乘原理，反演目标函数设置为

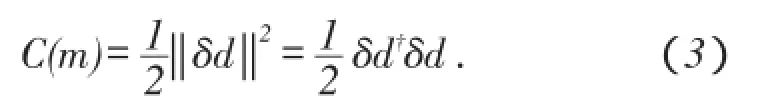
（3）式中目标函数C（m）的梯度计算可以通过正演波场P和散射波反传波场Q的零延迟互相关求解[10]：

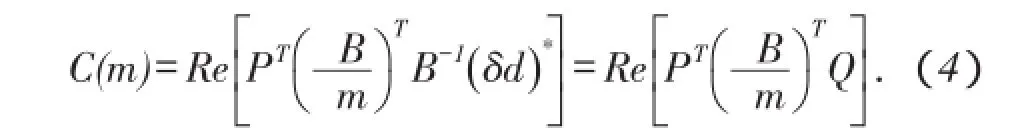
本文模型参数m即为速度模型，则速度模型沿共轭方向进行迭代更新有

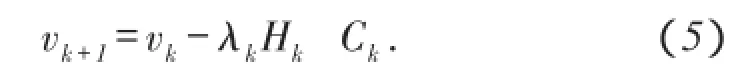
从（4）式中可以看出，计算目标函数的梯度需要2个正演计算：一个是震源激发所得到的波场；一个是剩余波场作为震源时所得到的反射传波场，也就是说，每次迭代过程都需要正演波场与散射波反传波场互相关来计算梯度∇Ck。

为避免反演结果陷入局部最小值，提高速度模型精度，首先，通过偏移速度分析获取一个较高精度的深度—速度模型，作为波形层析反演的初始速度模型；然后，对地震资料进行分析和测试选取反演频点；最后，应用多尺度波形层析反演，从低频反演到高频，低频输出结果作为高频反演的输入，迭代更新直至满足要求。

2　波形层析反演算法的有效性

Marmousi数值模型由法国石油研究院1988年提出，基于非洲西部Cuanza盆地Quenguele海槽北部Marmousi地区复杂地质构造而建立（图1）。Marmousi模型包含复杂的断层、不整合、隐伏的背斜构造以及盐丘穿刺现象（图1中红色区域）。1990年起，该模型成为美国勘探地球物理学会（SEG）用于验证各种成像方法能力和效果的经典模型[11]，利用常规速度建模方法难以获取重构该速度模型。二维Marmousi数值模型网格数设置为480×125，网格大小为5 m×5 m，模型横坐标x为0~2 400 m，纵坐标y为0~625 m.震源与检波器置于地表，单边放炮单边接收，每炮100道接收，震源间距10 m，检波器间距5 m，总炮数290，最小偏移距50 m，时间采样间隔为0.25 ms，每道2 018个采样点。波形层析反演的初始速度模型如图1b所示。

正演地震数据采用的震源为主频20 Hz雷克子波。为了对不同频率成分进行反演，对地震数据进行滤波处理。在波形反演问题上，选取3.54 Hz，4.76 Hz，9.65Hz，13.31Hz，16.97Hz，20.63Hz，24.39Hz，30.49Hz，36.60 Hz等10个频点。本文选择几个高频点，有利于反演模型中的细小结构。反演方式为前一个频点反演的结果是下一个频点反演的初始速度，每个频点最大迭代次数为20次。波形反演最终结果如图1c所示，经过波形层析反演迭代更新后的速度模型与真实的速度模型基本一致，较好地重构出了模型的真实属性，分辨率和精度均较高，证明了波形层析反演算法的可行性。

图2为不同频率的地震资料反演结果与真实值的比较。通过抽取图1中x=1 200 m处资料进行对比发现，随着反演频率的升高反演结果更趋于真实值。受子波主频及观测系统限制，速度变化较大的部分恢复得不理想；当子波频率增加到20 Hz，反演结果明显趋于真实模型。由此可见，该反演方法的分辨率主要依赖于地震记录的主频。

图1　不同的速度模型

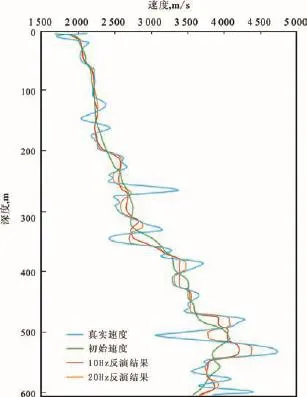
图2　反演结果、真实模型、初始模型在x=1 200 m处的速度剖面对比

3　实例验证

选取的实际资料为某海域地震资料，目标区水深约1 300 m，海底地层包含大量断层、隆起等复杂构造。选取一条拖缆采集数据，总共600炮，炮间距48 m，每炮960道接收。检波点间距6 m，最小偏移距156 m，最大偏移距5 916 m；接收记录长度为8 192 ms，时间采样间隔为2 ms.此次波形反演的目标层段深度为4 000 m，对应垂直旅行时约4 s.

3.1资料分析及处理

原始炮集资料如图3a所示，可以看出地震资料主要的干扰为多次波及线性噪声。为更好地重构出地层属性，对原始地震资料进行频谱分析，确定有效信号的频率范围。在此基础上进行一系列保幅处理，包括叠前去噪、异常振幅压制、振幅补偿以及子波处理等。影响地震振幅的因素主要考虑球面扩散补偿和地层吸收衰减。在地层吸收衰减方面，地震衰减因子Q由分析频谱比的方法计算得到，通过反Q滤波进行振幅补偿以消除地层衰减影响。由海上地震采集得到的远场子波对地震资料进行处理后，地震子波近似为雷克子波。图3b为处理后的地震资料，可以看出信噪比明显改善、目标层段内涌浪噪声和多次波得到较好压制。

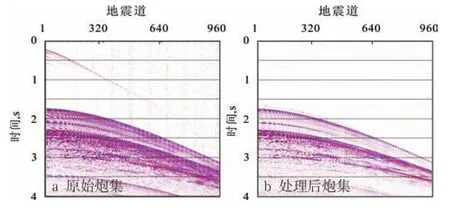
图3　保幅处理前后的炮集对比

3.2波形层析反演应用

基于叠前时间偏移剖面上地质层位解释结果，将时间域偏移速度分析结果转化为深度域。将深度域速度模型应用于叠前深度偏移迭代更新，作为波形层析反演的输入，以减小初始模型误差对反演结果的影响。图4a为建立的波形层析反演的初始输入模型，图4b为反演结果。可以看出，波形层析反演结果重构出了更多的高频信息。对于波形层析反演最终得到的速度模型，如何验证其可靠性是一个非常重要的问题。与模型试验不同，在实际应用中没有真实模型作为参照，并且本研究区勘探程度较低，无可用钻井资料。这时，一般采用的方法是基于该速度模型，对地震资料进行偏移成像和叠加，然后通过分析共成像点道集是否拉平以及叠加剖面来验证速度模型的质量。笔者采用叠前Kirchhoff深度偏移成像技术验证波形层析反演结果的质量。如果速度模型足够精确，偏移叠加剖面中层位的空间位置和连续性会较好。

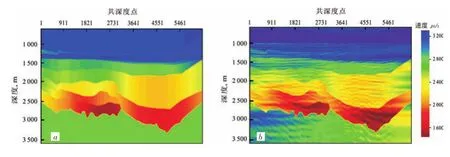
图4　波形层析反演更新前（a）后（b）速度模型对比

偏移叠加结果如图5所示，对比发现，波形层析反演更新前后的成像效果整体上基本一致，但是更新后的成像效果有了一定程度的改进，连续性和分辨率更高，特别是红色椭圆和绿色框内的陡构造成像清晰，成像效果显著改善。但是，在局部位置效果不太理想，甚至是变差，例如黄色椭圆框内的同相轴。分析其原因，主要有：地震资料缺失低频信息，导致构建的模型与实际地质模型产生差距，在低频模型基础上计算出的相对速度存在误差，速度搜索有震荡趋势，使这一“病态”的反演问题极易陷入局部极小，难以获得全局最优解；另外，叠前Kirchhoff偏移方法基于高频近似假设，适用于较平滑模型，而波形层析反演在速度建模时可能会产生不规则的高频速度扰动信息，影响其适用性。后续研究中，波形层析反演结果的验证最好采用一些高精度的叠前深度偏移成像方法，例如逆时偏移等。总体来说，更新后的成像效果更好。沿剖面上的实线位置抽取偏移距域共成像点道集进行分析（图6），可以发现，波形层析反演方法对应的共成像点道集波组特征更加丰富，同相轴更加平整。

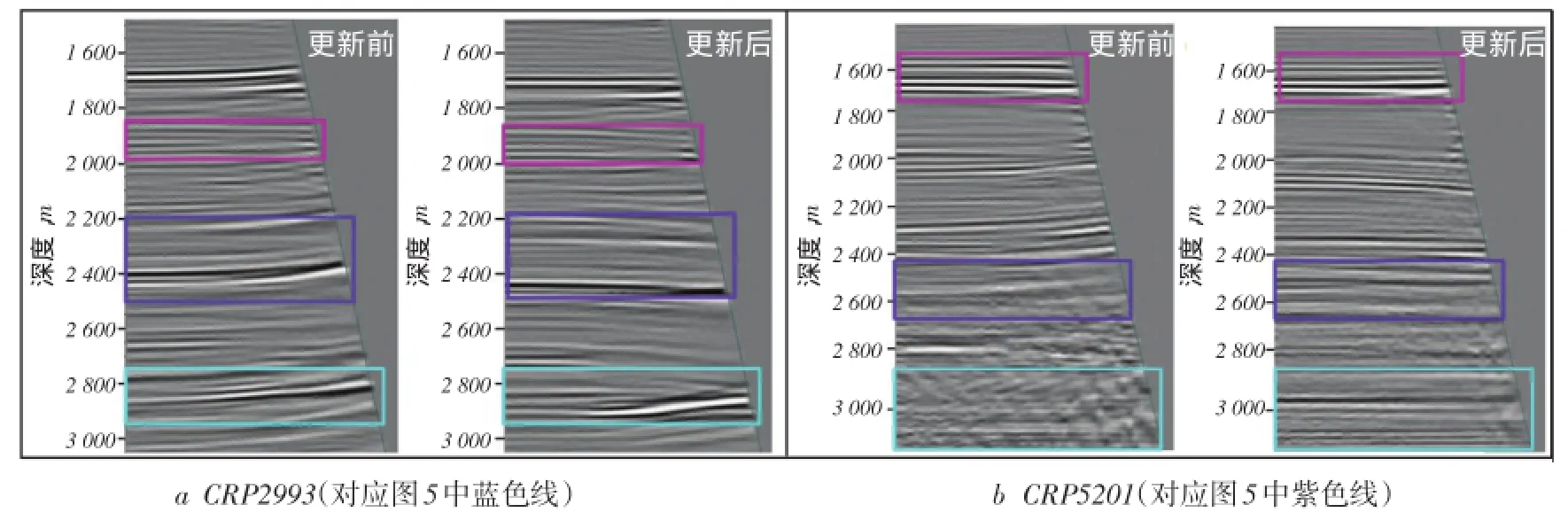
图6　波形层析反演更新前后对应的偏移距域共成像点道集对比

4　结论与认识

（1）偏移速度分析可以为波形层析反演提供一个相对较好的深度域速度模型，从而提高反演结果的精度和计算效率。

（2）从扰动波场重构的角度进行正演分析，识别出速度扰动对应的反射特征，选择优势频点进行反演，将其应用于实际资料反演可得到更为可靠的反演结果。

（3）基于高频近似假设的Kirchhoff叠前深度偏移，得到的速度仅包含了速度场中的低波数成分，同时建模过程工作量大、人为参与多，适应性受到一定限制。在其他构建速度模型的方法（如旅行时层析等）中，以及适当加入井约束信息控制，可提供准确的初始速度模型，从而提高波形层析反演质量，在这些方面还需要多做些探索性研究。

符号注释

B——差分方程稀疏矩阵;

dobs——实际地震记录；

dcal——波场正演记录；

Hk——近似Hessian矩阵；

k——迭代次数；

m——模型参数；

P——未知波场；

P——未知正演波场向量;

Q——散射波反传波场，Q=B-1(δd)*；

Re——取复数的实部；

S——震源函数；

S——震源向量；

v——速度,m/s；

vk——第k次迭代的速度模型；

ω——角频率,rad/s；

λ——迭代步长，可通过二次方程线性搜索得到；

T——转置算子；

†——共轭转置算子;

*——共轭算子。

［1］Qin N,Li Z,Yang X.Tomography velocity modeling and application in marine carbonate reservoirs［C］.Expanded Abstracts of SPG/ SEG International Geophysical Conference,2011:1 211-1 216.

［2］王喜双，梁奇，徐凌，等.叠前深度偏移技术应用与进展［J］.石油地球物理勘探，2007，42（6）：727-732. Wang Xishuang,Liang Qi,Xu Ling,et al.Application and progress of prestack depth migration technology［J］.Oil Geophysical Pros⁃pecting,2007,42（6）:727-732.

［3］张敏，李振春.偏移速度分析与建模方法综述［J］.勘探地球物理进展，2007，30（6）：421-427. Zhang Min,Li Zhenchun.Review of migration velocity model build⁃ing［J］.Progress in Exploration Geophysics,2007,30（6）:421-427.

［4］刘百红，任跃华，陈国金.偏移速度分析与速度反演方法评述［J］.CT理论与应用研究，2013，22（4）:727-740. Liu Baihong,Ren Yuehua,Chen Guojin.Review on migration veloc⁃ity analysis and inversion［J］.CT Theory and Applications,2013,22（4）:727-740.

［5］Vigh D,Starr E W,Kapoor J.Developing earth models with full waveform inversion［J］.The LeadingEdge,28（4）:432-435.

［6］Wang Y,Wallace K.Acoustic full waveform inversion using reflec⁃tion energy:a case study from the Ekofisk LoFS ocean bottom datas⁃et［C］.Expanded Abstracts of 83rd SEG Annual International Meet⁃ing,2013:908-912.

［7］Gauthier O,Virieux J,Tarantola A.Two⁃dimensional nonlinear in⁃version of seismic waveforms:numerical results［J］.Geophysics, 1986,51（7）:1 387-1 403.

［8］Diet J P,Jones I F.Strategic seismic imaging:a stepwise approach to 3⁃D prestack imaging of complex structures［C］.Expanded Ab⁃stracts of64thSEG AnnualInternationalMeeting,1994:1242-1245.

［9］Bunks C,Saleck F M,Chavent G.Multiscale seismic waveform in⁃version［J］.Geophysics,1995,60（5）:1 457-1 473.

［10］唐志远.基于叠前地震反演的复杂含油气储层预测与成像方法研究［D］.北京：中国石油大学，2013. Tang Zhiyuan.Study of pre⁃stack seismic inversion in reservoir prediction and imaging method［D］.Beijing:China University of Petroleum,2013.

［11］Gary S,Robert W,Kurt J.Marmousi2:an elastic upgrade for Mar⁃mousi［J］.The LeadingEage,2006,25（2）:156-166.

Application of Multiscale Waveform Tomography Inversion in High⁃Accuracy Velocity Modeling

MA Yiming1,SUN Zandong1,TANG Zhiyuan2,YU Liwen1
(1.Laboratory for Integration of Geology&Geophysics,ChinaUniversity of Petroleum,Beijing 102249,China;2.CNOOC Energy Development EngineeringBranch,Tianjin 300457,China)

The information of seismic amplitude and phase for reconstruction wave field can be used in waveform tomography inversion method to get a velocity model with higher accuracy and resolution theoretically.However,because of its serious nonlinearity and high de⁃pendence on initial velocity model,it often results in unsatisfactory inversion results in field application.This paper presents an improved strategy of multiscale inversion to establish higher⁃accuracy depth migration velocity field as an initial input model of waveform tomogra⁃phy,so that decrease the serious nonlinearity.This strategy is successfully applied to Marmousi model and case study,in which the updated velocity is used to make Kirchhoff pre⁃stack depth migration.The final result shows that the waveform tomography can retrieve much more high⁃frequency details and highly improve the accuracy and resolution of the seismic migration imaging.

multiscale;wave equation;waveform tomography;velocity modeling

P631.445.7

A

1001-3873（2015）04-0493-05

10.7657/XJPG20150421

2015-01-19

2015-04-27

国家973项目（2011CB201103）；国家科技重大专项（2011ZX05004003）

马一鸣（1990-），男，湖北大冶人，硕士研究生，地球物理勘探，（Tel）15311313986（E-mail）cup_maym@126.com.

叠前深度偏移，成像结果与抽取的偏移距域共成像点道集对比结果显示，多尺度波形层析反演更新了更多的高频细节信息，提高了地震偏移成像的精度和分辨率。