Hydraulic mechanism and time-dependent characteristics of loose gully deposits failure induced by rainfall

Yong Wu*,Siming He

aKey Laboratory of Mountain Hazards and Earth Surface Process，Chinese Academy of Sciences，Chengdu，610041，China

bInstitute of Mountain Hazards and Environment，Chinese Academy of Sciences，Chengdu，610041，China

cState Key Laboratory of Geohazard Prevention and Geoenvironment Protection，Chengdu University of Technology，Chengdu，610059，China

Hydraulic mechanism and time-dependent characteristics of loose gully deposits failure induced by rainfall

Yong Wua,b,c,*,Siming Hea,b

aKey Laboratory of Mountain Hazards and Earth Surface Process，Chinese Academy of Sciences，Chengdu，610041，China

bInstitute of Mountain Hazards and Environment，Chinese Academy of Sciences，Chengdu，610041，China

cState Key Laboratory of Geohazard Prevention and Geoenvironment Protection，Chengdu University of Technology，Chengdu，610059，China

A R T I C L EI N F O

Article history：

in revised form

24 August 2015

Accepted 6 September 2015

Available online 9 October 2015

Loose deposits

Time-dependent characteristics

Groundwater lever

Hydraulic mechanism

A B S T R A C T

Failure of loose gully deposits under the effect of rainfall contributes to the potential risk of debris flow. In the past decades,researches on hydraulic mechanism and time-dependent characteristics of loose deposits failure are frequently reported,however adequate measures for reducing debris flow are not available practically.In this context,a time-dependent model was established to determine the changes of water table of loose deposits using hydraulic and topographic theories.In addition,the variation in water table with elapsed time was analyzed.The formulas for calculating hydrodynamic and hydrostatic pressures on each strip and block unit of deposit were proposed,and the slope stability and failure risk of the loose deposits were assessed based on the time-dependent hydraulic characteristics of established model.Finally,the failure mechanism of deposits based on infinite slope theory was illustrated,with an example,to calculate sliding force,anti-sliding force and residual sliding force applied to each slice.The results indicate that failure of gully deposits under the effect of rainfall is the result of continuously increasing hydraulic pressure and water table.The time-dependent characteristics of loose deposit failure are determined by the factors of hydraulic properties,drainage area of interest,rainfall pattern, rainfall duration and intensity.

©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by

Elsevier B.V.All rights reserved.

1.Introduction

In the western mountains of China,the I-II ladders alternating zones arebasicallycharacterized with strong tectonic stress and the faults are well-developed,leading to serious denudation in the mountains and/or frequent landslide subsequently.When a large amount of clastic material accumulates in the gully,this would significantly increase the risk of the occurrence of debris flow in valley.

To date,the fluidization of loose geomaterials due to rainfall has beenextensivelystudied.HutchinsonandBhandari（1971）concluded that the debris flow is a combined result of shear strength reduction of loose deposits and increase of pore pressure when the drainage condition is poor.Xu et al.（2002）studied the formation process of debris flow by flume experiment and discussed the mechanism of mudslides on different longitudinal slopes.Cui（1991）applied the Mohr-Coulomb criterion to debris flow by flume experiments.Hu and Wang（2003）established a model with respect to water content to verify the coexistence of landslide and debris flow by artificial rainfall experiments.Chen（2006a）proposed a softening and liquefaction mechanism of the soil-mechanical debris flow by field observation and laboratory tests.Hu（2008）researched the fractal characteristics of gully development and the stability of debris flow body,and illustrated the disaster mechanism of loose accumulation when slip surface soil begins to liquefy.Chen et al.（2012）qualitatively illustrated the runout characteristics of debris flow by field study at Xiaojiagou characterized with huge loose materials caused by‘5.12'Wenchuan earthquake.Ni（2015）experimentally studied the initiation mechanism of gully-type debris flow with artificial rainfall and runoff, and he also proposed the relations between rainfall intensity and gully erosion,failure mode of soil mass,initiation mechanism and characteristics of debris flow.

Concerning the debris flow,various researchers considered some critical factors,such as grain composition and bed slope critical water content,in their studies.Xu et al.（2009）analyzed the failure mechanism of slagheap by model tests.Guo et al.（2013）studied the debris flow triggering threshold considering antecedent rainfall through a case study in Jiangjia Ravine.Zhou et al.（2013）conductedasurfacewaterrunoffandsaturated-unsaturated seepage to numerically model rainfall infiltration and runoff on a slope,and they analyzed the triggering mechanism of debris flow caused by landslide deposits.Wang et al.（2015）proposed debris flow formation process by exploring the permeability characteristics and critical hydrodynamic conditions of loose deposits in Guojuanyan Gully triggered by earthquake.

Gully collapse deposit usually has loose structure,large porosity and high permeability,which makes its hydraulic properties different from those of flow sediment body.Thus groundwater flow moves with strong time-dependent characteristics.However,most of above-mentioned studies on fluidization of loose geomaterials do not consider the gully loose deposits in mountains with hydraulic properties.Meanwhile,the time-dependent hydraulic mechanism is notwell understood.In fact,many factors,such as the structural and mechanical properties of the sediment materials,the rainfall intensity and duration,could influence the initiation of debris flow and should be considered in the model（Iverson and LaHusen,1989；Kotarba,1997；Chen,2006b；Zhang et al.,2011）. Therefore,the traditional theories about the stability and fluidization of loose deposits cannot be used directly to explain the failure mechanism of gully loose deposit accumulated in mountains.

In this study,the time-dependent characteristics of loose deposits caused by different patterns of rainfalls are studied and the water table model is established accordingly based on hydrological and hydraulic theories.By analyzing the variation of hydraulic pressurewhenwater table changes,the calculation formulas for the stability of gully loose deposits are proposed.Finally,the failure mechanism of accumulation body is illustrated with a case study.

2.Time-dependent model of water table in gully loose accumulation body

The gully debris flow is mainly characterized by narrow steep channels,abundant sediment,and heavy and intense rainfall.In order to study the debris flow mechanism,a simple water table model is built based on the following assumptions：

（1）The loose accumulation body is mainly composed of sand and rubble,which have high permeability.

（2）The permeability of gully bed is significantly small that it can be ignored.

（3）No evaporation occurs in the catchment basin of interest.

According to Fig.1,the water that converges in gully can be expressed as

QIN（t）=I（t）A（1）

where A is the area of upper catchment basin；QIN（t）is the water that flows into the accumulation body with respect to time t；I（t）is the basin rainfallintensity,which is the function of time t and varies with respect to vegetation interception,soil infiltration,evapotranspiration,etc.

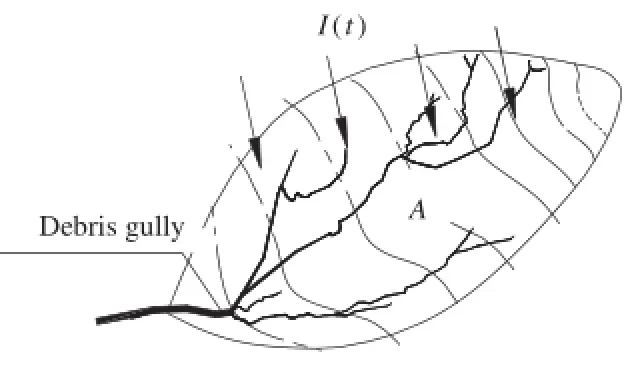
Fig.1.Catchment basin of gully debris flow.

Obviously,water accumulated from catchment basin of interest increases unevenly with increase of rainfall duration t.Thus,the rainfall volume during an infinitesimal time［t,t+dt］can be calculated as

VIN=QIN（t）dt=I（t）Adt（2）

Meanwhile,water that flows into the accumulation body can also flow out under the action of hydraulic pressure.As shown in Fig.2,assuming the accumulation body has width of w and thickness of Z,the water that flows out of the accumulation body can be calculated by

QOUT=kwh（t）i（3）

where k is the permeability coefficient；QOUTis the water that flows out of the accumulation body；h（t）is the water depth of accumulation body；i is the hydraulic gradient,which can be expressed as sinθwith respect to the gully bed dip angleθ.

Similarly,the volume of water which flows out of the accumulation body during an infinitesimal time［t,t+dt］can be calculated as

VOUT=QOUTdt=kwih（t）dt（4）

Theoretically,water table varies with the changes of water volume in the accumulation body.When VINis different from VOUT, the depth of water can be expressed as follows according to Eqs.（2）and（4）：

I（t）Adt-kwih（t）dt=V（5）

where V is the water volume changes in the accumulation body, which can be expressed as

V=we（1-Sr）dh（t）（6）

where e and Srare the porosity and degree of saturation of the accumulation body,respectively.

The rainfall process can roughly be divided into several time intervals based on intensity peaks.As shown in Fig.3,assuming the rainfall intensity obeys power law during a time interval［ta,tb］,it can be modeled as

I（t）=Im-η|t-tm|n（ta≤t≤tb）（7）

where Imis the peak value of rainfall intensity during a time interval［ta,tb］；tmis the moment when Imappears；ηis the rainfall intensity coefficient；n is a nonnegative integer which has different values between intervals［ta,tm］and［tm,tb］.

Combining Eq.（6）with Eq.（7）yields

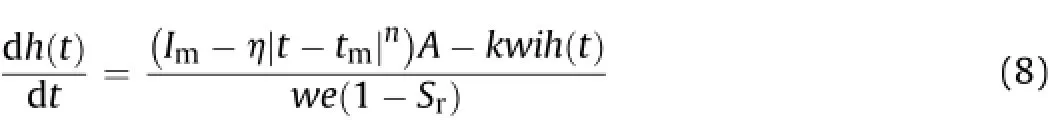
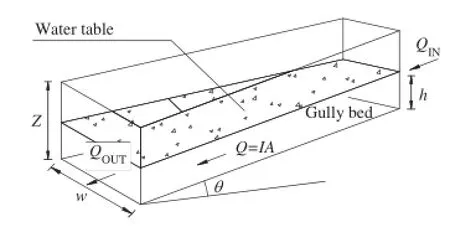
Fig.2.Hydrological model of gully accumulation body.

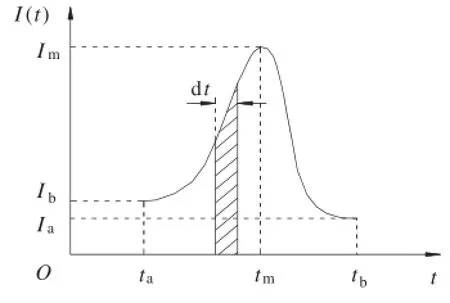
Fig.3.Model of a peaks interval of rainfall.

By solving Eq.（8）,the general solution of water table in the accumulation body can be given as

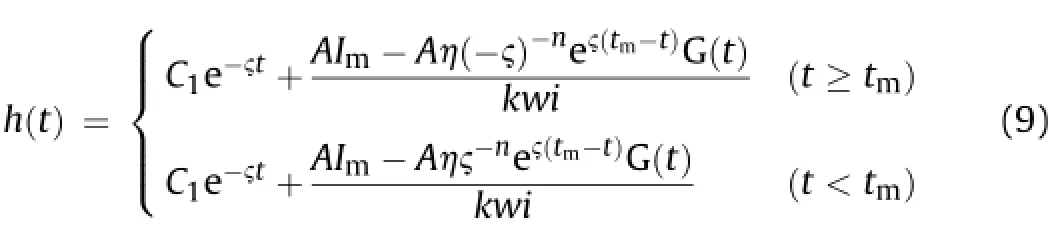
where

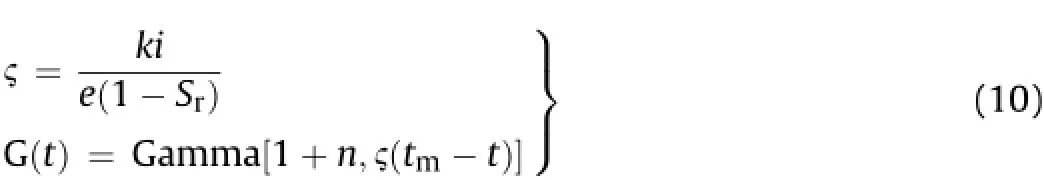
where Gamma［1+n,ζ（tm-t）］is the Gamma function；C1is a random constant when the boundaryconditions such as ta,Iaand haare known in a rainfall,where hais the initial value of water level.

It is notable that the water table is influenced by watershed features,soil hydraulic properties and rainfall characteristics.For a site-specific gully,the rainfall pattern plays an important role in the failure of gully deposits.

3.Variation of water table in different patterns of rainfall

In practice,the rainfall could be divided into different patterns such as uniform,linear,parabolic.In order to understand the timedependent characteristics of the failure of gully loose deposits in rainfall,the variation of water table is determined,assuming that the initial water table h0and the rainfall pattern are a priori known.

3.1.Time-dependent characteristics of deposit failure under uniform rainfall As is shown in Fig.4a,the intensity of uniform rainfall is a constant value.Therefore,n=0,η=0,and Eq.（7）can be simplified as

I（t）=Im（11）

Accordingly,the water table of accumulation body obtained by Eq.（9）can be simplified as

Fig.4.Intensity curves of three patterns of rainfall.

h（t）=ξ1+ξ2e-ξ3t（12）

where

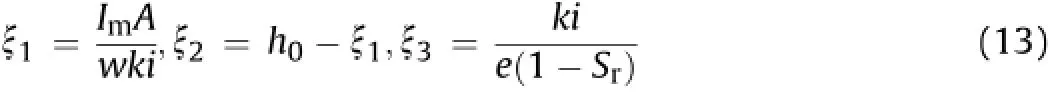
In the uniform rainfall pattern,the water table is an exponential function oftime.As shownin Fig.5,when the intensity Im=I1＞kwih0/A,the water table h（t）rises exponentially with time tandeventuallyapproachesI1A/（kwi）.Conversely,when Im=I2＜kwih0/A,the value of h（t）decreases with t and eventually approaches I2A/（kwi）.When Im=I0=kwih0/A,the water table in loose deposits keeps constant as h0.It is noted that water table keeps at low level in slight rain and excess water would be drained from deposits.Whereas,large uniform rainfall intensity inevitably leads to the rise of water table and causes debris flow.

It should be emphasized that when Im=0,Eq.（12）indicates the dissipation of groundwater in deposits.

3.2.Time-dependent characteristics of deposit failure under linear rainfall

As shown in Fig.4b,the intensity of linear rainfall increases or decreases linearly with time.Thus n=1 and Eq.（7）can be simplified as

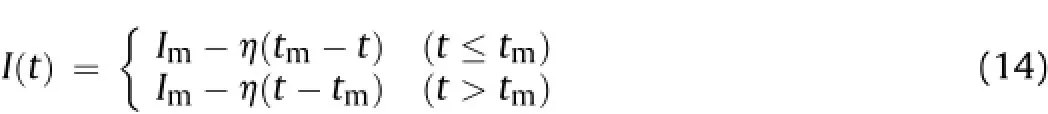
Accordingly,the water table in accumulation body in Eq.（9）can be simplified as

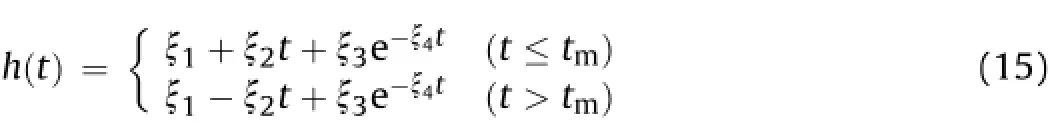
where

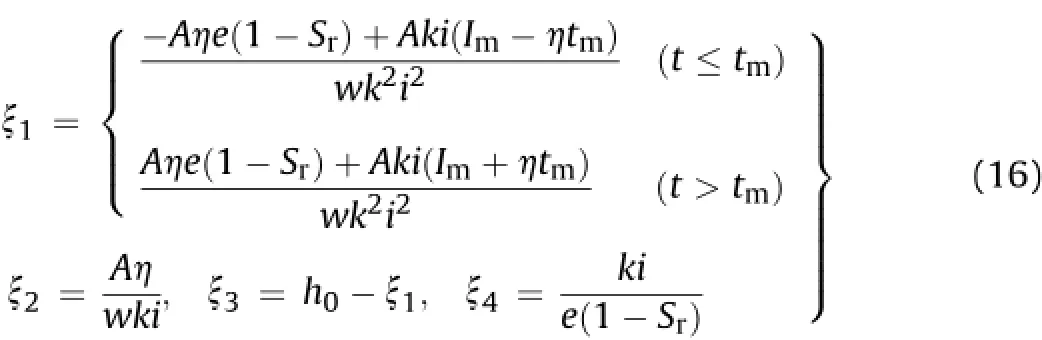
Obviously,in the linear rainfall pattern,the water table is an exponential and linear function of time.Normally,the exponential form is of priority at the beginning of rainfall,and the linear form is gradually dominant afterwards.

Fig.5.Curves of groundwater table under uniform rainfall pattern.

（1）The rainfall intensity increases linearly when t＜tm.If the intensity peak of the rainfall Imis equal to I0=kwih0/ A+ηe（1-Sr）/（ki）+ηtm,the water table rises linearly,i.e. h（t）=h0+ξ2t.As shown in Fig.6a,when Im=I1＞I0,the water table h（t）rises exponentially with time t at the beginning and then rises linearly while h（t）=ξ1（I1）+ξ2t.Conversely,when Im=I2＜I0,the water table h（t）falls exponentially at the beginningandthenriseslinearly,thenwehave h（t）=ξ1（I2）+ξ2t.

（2）The rainfall intensity decreases linearly when t＞tm.If the intensity peak of rainfall Imis equal to I0=kwih0/A-ηe（1-Sr）/（ki）-ηtm,the water table h（t）decreases linearly,following h（t）=h0+ξ2t.As shown in Fig.6b,when Im=I1＞I0,the water table h（t）rises exponentially with time at the beginning and then decreases linearly,i.e.h（t）=ξ1（I1）-ξ2（t-tm）.Conversely, when Im=I2＜I0,the water table h（t）falls exponentially at thebeginningandthendecreaseslinearly,i.e.h（t）= ξ1（I2）-ξ2（t-tm）.

It shows that the water table increases or decreases with the same linear ratio under linear rainfall pattern with different values of Im,even if water table plays different roles at the beginning of rainfall.

3.3.Time-dependent characteristics of the deposits failure in parabolic rainfall

As shown in Fig.4c,the intensity of parabolic rainfall pattern is a quadratic function of time.Thus,we have n=2 and Eq.（7）can be simplified as

I（t）=Im-η（t-tm）2（0≤t≤tmax）（17）

Accordingly,the water table in the accumulation body in Eq.（9）can be given as

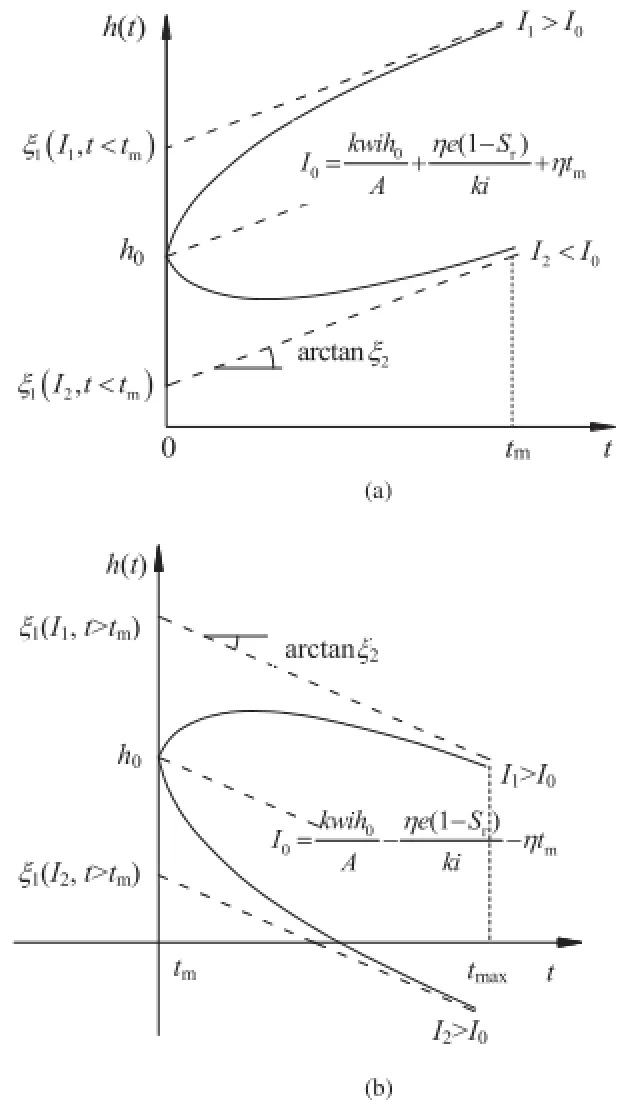
Fig.6.Curves of water table in linear rainfall pattern.

h（t）=ξ1+ξ2t-ξ3t2+ξ4e-ξ5t（18）

where

In Fig.7,when Imis equal to I0=2ηe（1-Sr）2/（ki）2+ ηtme（1-Sr）/（ki）+kwih0/A+,thewater table h（t）changes with a parabolic curve h（t）=ξ1+ξ2t+ξ3t2；when Im=I1＞I0,the water table rises quickly with an exponential-linear function at the beginning and then follows the parabolic rate law until h（t）=0.On the contrary,if Im=I2＜I0,the value of h（t）would decrease exponentially first and then increase slightly,but eventually decreases following the parabolic rate law until t＞tm.Obviously,the water table in a parabolic rainfall is a composition function,and is mainly controlled by exponential function at the beginning and then follows the parabolic rate law.

4.Stability analysis of gully loose deposits

The structure of gully loose deposits is basically featured with large void ratio and high permeability.Rainfall in rainy season rapidly increases water flow in gully,continuously uplifts the water table of deposits,and changes its hydraulic environments,which could lead to instability of the deposits.

Due to the gradient of gully bed,the thickness and width of deposits differ in various locations of natural gully.Therefore,the loose deposit can be divided into n slices for the purpose of stability analysis.As shown in Fig.8,the average thickness,width and slope gradient of slice i are Zi,wi,andθi,respectively.Assuming that the water table hiin the slice i is known,the hydraulic characteristics and stability of deposits can be analyzed subsequently.

4.1.Hydraulic action on gully loose deposits

Fig.9 shows the hydraulic action of groundwater on loose deposits of the slice i.We assume that the free heads at points A and B are hAand hB,respectively,the hydrostatic pressures vertical to gully bed at points A and B are

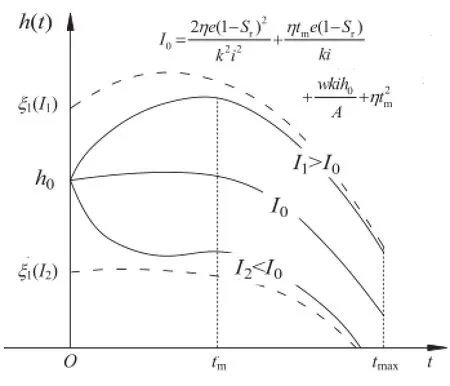
Fig.7.Curves of groundwater table under parabolic rainfall.

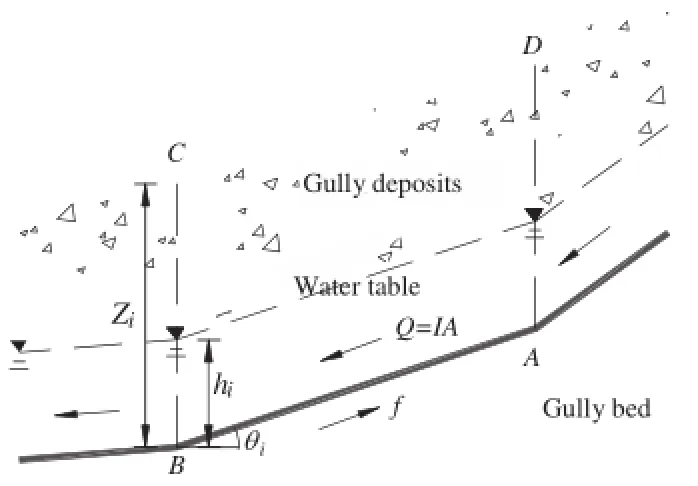
Fig.8.Calculation model of gully loose deposits.

pA=γwhA,pB=γwhB（20）

whereγwis the unit weight of groundwater.

Taking point A as the origin and x-axis along AB,the distribution of hydrostatic pressure on AB can be expressed as

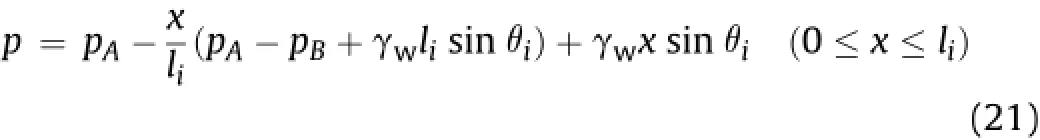
where liis the length of the slice i.

Integrating x in Eq.（9）,the equivalent concentrated force of hydrostatic pressure at the bottom of the slice i can be obtained：

where hi=（hA+hB）/2 is the average water table in the slice i.

In addition,dynamic water pressure can also be generated when groundwater flows through the continuous fillings,which decreases the deposits stability directly by dragging deposits body downward（Zhang and Bai,2003；Li and Guo,2007）.According to the continuum theory（Chai and Wu,2001）,the dynamic pressure in the slice i with unit width of deposits can be written as

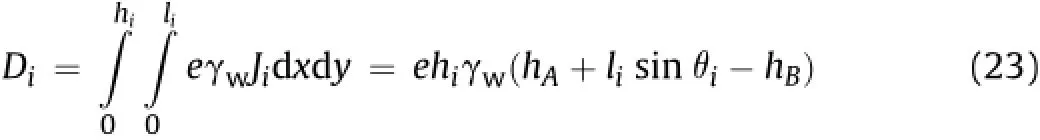
where Jiis the hydraulic gradient.

Normally,the head lossδof groundwater for per unit following the lengthof thedeposits is establishedand can be gained bymodel test.So Eq.（23）can be simplified as

Di=ehiγwδli（24）

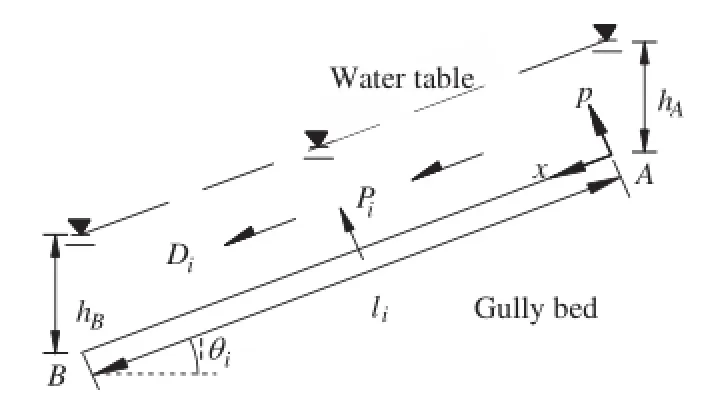
Fig.9.Hydraulic action of groundwater on loose deposits.

4.2.Stability analysis of loose deposits

As shown in Fig.10,the stability of slice i of loose deposits in gully is determined by inter-slice forces Miand Mi-1,mass Gi, resultant normal force Ni,and shear resistance fi.The stability of deposits decreases when the groundwater begins to flow because of hydraulic action,which has been mentioned previously.

The sliding force on the slice i,Ti,can be expressed as

Ti=Di+Mi-1cos（θi-1-θi）+Gisinθi（25）

In particular,when i=1,Mi-1can be obtained as M0=0. Similarly,when i=n,Miis given as Mn=0.

The anti-sliding force on the slice i can be expressed as

Fi=Mi+fi（26）

where fiis the average shear strength,which can be given by the Mohr-Coulomb failure criterion as follows：

fi=cli+［Gicosθi+Mi-1sin（θi-1-θi）-Pi］tan φ（27）

where φ is the internal friction angle and c is the cohesion of loose deposit.

Obviously,when the slice i keeps stable under the condition that Ti＜Fi,the slices from 1 to i-1 are also theoretically stable. Especially,if the condition of Tn≤Fncan be satisfied,the whole deposit will be stable.Hence,the safety factor of loose deposits in gully can be expressed as

It is notable that the deposits will fail locally when the slice i is stable but the slice i+1 is unstable.

5.Case analysis

A typical loose deposit in Chayuan Gully in Sichuan Province is presented here.The deposit is located in the right bank of Zagunao River with a length of 8.9 km and area of 19.4 km2（Liu et al.,2004）. The gully is filled with sandstones caused by collapse of slopes on both sides,which results in serious debris flow in every rainy season.

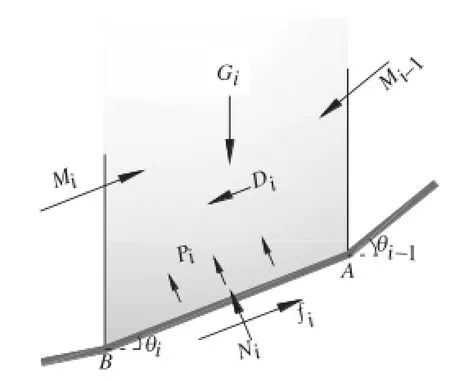
Fig.10.Force analysis of slice element.

According to field survey,the loose deposit is mainly located at the entrance of gully with average width and length of 8 m and 200 m,respectively.The initial water table in deposits is 0.8 m.As shown in Fig.11,the deposits can be divided into slices AB,BC,and CD according to the parameters of gully bed gradient,which are obtained by field investigation and are shown in Table 1.In order to understand the failure mechanism of loose deposits during rainfall, the intensity of rainfall is given in Fig.12,and the physico-mechanical parameters of gully materials are obtained by laboratory tests and listed in Table 2.

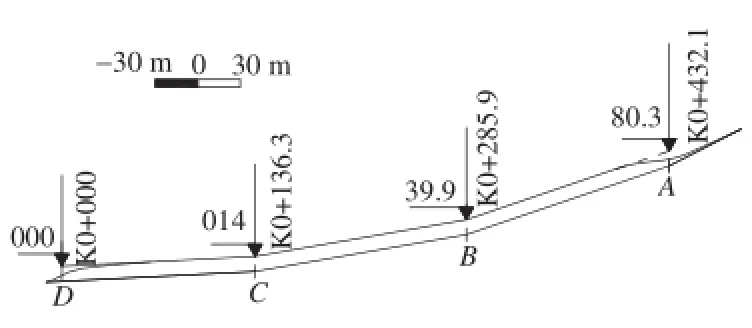
Fig.11.Longitudinal profile of gully deposits mass.

Table 1　Geometric parameters of gully bed.

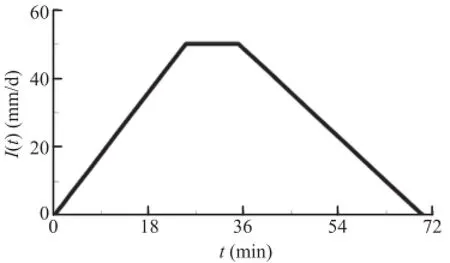
Fig.12.Intensity of effective rainfall in basin.

5.1.Time-dependent characteristics of water table in rainfall

As shown in Fig.12,the intensity of rainfall increases linearly from 0 to 25 min.According toTable 1 and using Eqs.（14）-（16）,the water table is obtained and shown in Fig.13.It is indicated that,the water table in those three slices of deposits rapidly decreases exponentially and reaches the minimum at around 50 s,and then begins to rise linearly.It is indicated that the groundwater runs off in the deposits when the rainfall recharge capacity is not high enough at the beginning.Besides,it is also observed that the water table in slices with smaller gradient rises faster as shown in Fig.13.

Theoretically,during 25-35 min,the water table would rise exponentially.In fact,the water table as shown in Fig.14 only rises in first few minutes and then keeps stable.For example,the water table in slice CD rises from 7.64 m to 7.68 m during 25-26.2 min, and then almost keeps constant,which indicates that a stable rainfall usually leads to a stable water level.

Fig.15 shows the water table decreases linearly with respect to rainfall.Similar to linearly increased rainfall pattern,the water table shows a composited exponential-linear function and decreases linearly during the whole period of time except the early stage of this period.

As shown in Fig.16,the residual water table in slice CD is the highest（0.146 m）at the end of rainfall（70 min）,which is 7 times that in slice AB（0.022 m）.In the following 75 min,the residual water table in slice CD falls exponentially to 0.Although the gradient of slice CD is smaller,the groundwater runs off more quickly than that in the other two slices due to a higher residual water table,suggesting that the amount of residual groundwater is also an important factor that affects the speed of discharge.

5.2.Hydraulic characteristics of deposits

The sliding force on each slice is calculated by Eq.（27）and is shown in Fig.17.It is evident that the sliding force on slice AB is the largest assuming that all slices have a similar gravity,which indicates that the gradient plays an important role in sliding force.In addition,the sliding forces on slices are markedly related to water table.Taking the slice CD for an example,it can be seen that：（1）The sliding force decreases firstly and then increases rapidly with respect to linearly increased rainfall pattern；（2）The sliding force keeps steady comparatively in association with steady rainfall pattern；（3）The sliding force decreases continuously to a stable valuewith linearly decreased rainfall and afterrainfall,respectively.

The anti-sliding force on each slice is shown in Fig.18.It is observed that the anti-sliding force is governed by deadweight, slope gradient,water level and residual sliding force,and is closely correlated with water table.Taking the slice BC for an example,it is shown that：（1）During the first 12 min after rain beginning and the last 22 min of raining,the anti-sliding force is large due to the low water table and large deadweight,and the residual sliding force is zero（Table 3）.（2）During the raining time from 12 min to 53 min, the anti-sliding force is correlated with water table and slope gradient due to the strong hydraulic action.

Table 2　Physico-mechanical parameters of gully material.

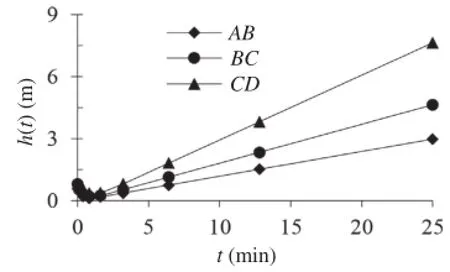
Fig.13.Curves of water table in linearly increased rainfall pattern.

Fig.14.Curves of water table in uniform rainfall pattern.

As shown in Fig.19,the stability of each slice is also correlated with the water table.At the beginning of raining,the water table is lowand the stability of each slice is good,especially for the slice CD, whose stability coefficient is up to 3.34.With increase in rainfall intensity and duration,the water table increases continuously, while the stability of deposits decreases continuously.During the period from 20 min to 40 min,the sliding force of slice AB with thesteepest slope is greater than its anti-sliding force.In reality,the slice AB would not fail due to the transfer of residual sliding force. Finally,the stability of each slice increases continuously up to the maximum as the rainfall linearly decreases and eventually stops.

During the whole time,the stability coefficient of slice CD is larger than 1,which indicates that not only the slice CD but also the whole deposits are stable in a global sense.

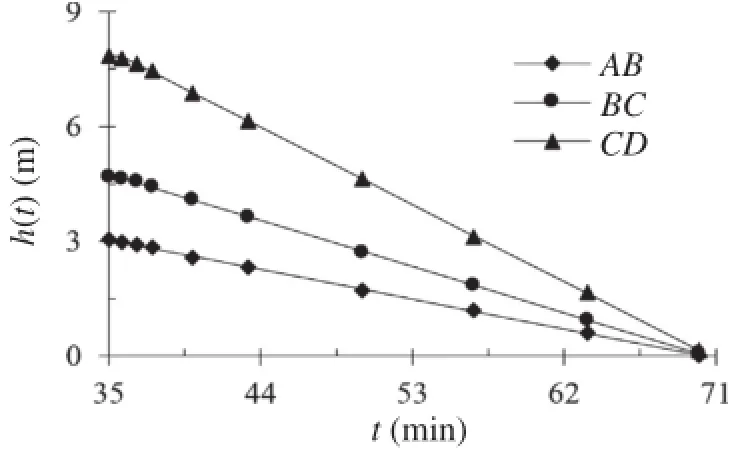
Fig.15.Curves of water table decreasing linearly with respect to rainfall.

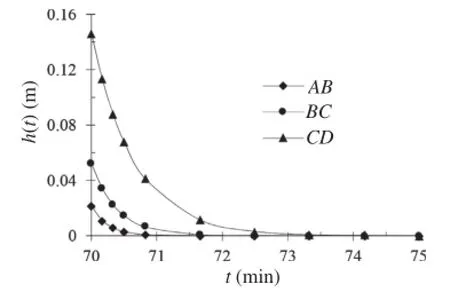
Fig.16.Curves of water table after rain.

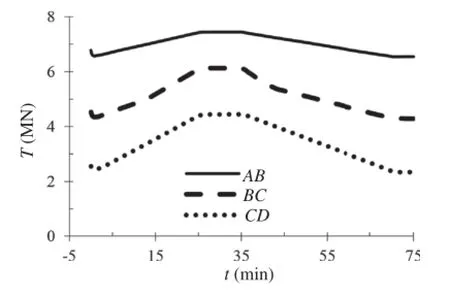
Fig.17.Sliding forces on different slices of deposits.

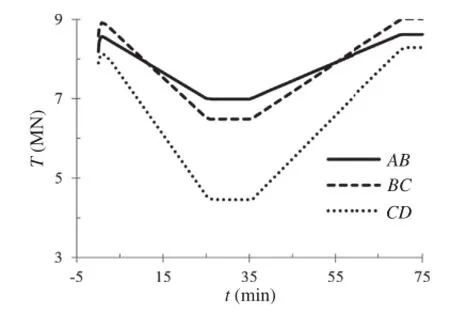
Fig.18.Anti-sliding forces on different slices of deposits.

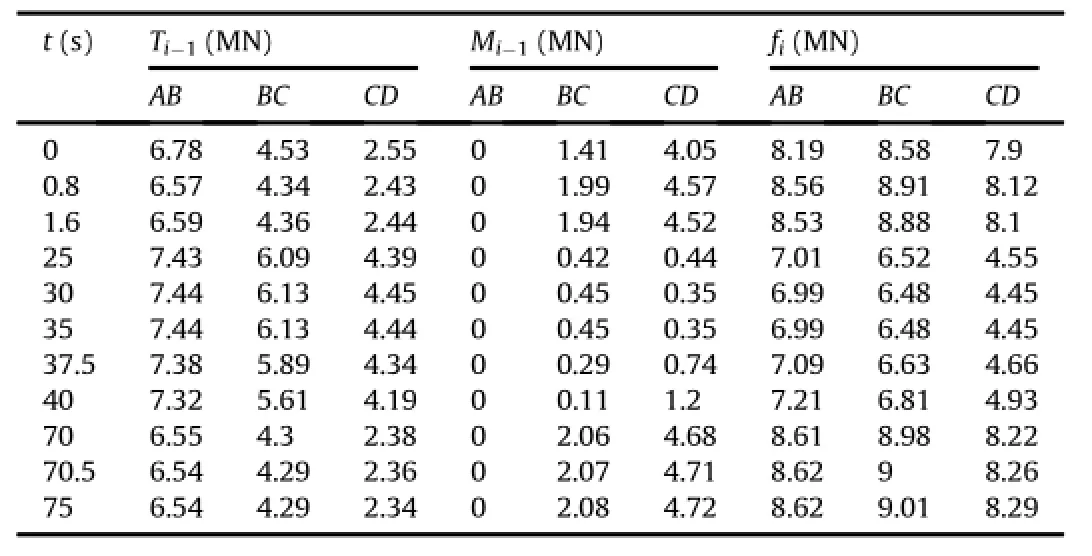
Table 3　Loads imposed on different parts of mass at different times.

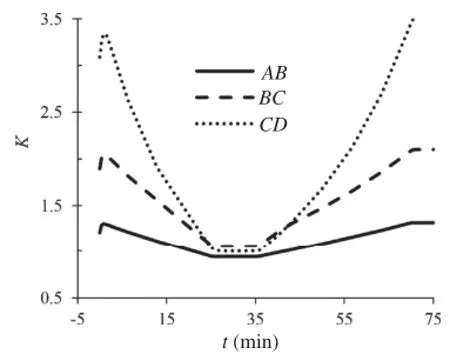
Fig.19.Stability coefficients of deposits body with time.

6.Conclusions

In this context,the water table model of gully loose deposits is established and its time-dependent characteristics in association with different patterns of rainfall are studied on the basis of hydrological,hydraulic and topographic theories.The hydraulic characteristics and hydraulic pressure with rising water table are analyzed and the calculation formulas for stability of gully loose deposits are proposed.The following conclusions can be obtained：

（1）The failure of gully deposits in rainfall is the result of increment of hydraulic pressure with respect to the rise of water table.

（2）The water table is influenced by watershed features,soil hydraulic properties and rainfall characteristics.For a site-specific gully,the water table is governed by rainfall pattern.

（3）If the duration of rainfall is long enough,the water table would keep steady in uniform rainfall pattern,while it would rise or fall with linearly increased or parabolic rainfall pattern.

（4）The residual groundwater in deposits discharges eventually if the rainfall intensity is small,while groundwater would be supplied in heavy rains.

（5）The rise of water table in deposits not only enhances the hydrostatic pressure that weakens the anti-sliding force,but alsoincreases the dynamic hydraulic pressure that enhances the sliding force of deposits.

Conflict of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgment

This work was supported by the National Natural Science Foundation of China（Grant No.41202258）,STS Project（Grant No. KFJ-EW-STS-094）,Research Plan Project of China Railway Eryuan Engineering Group Co.,Ltd.（Grant No.13164196（13-15））,and the State Key Laboratory Project Fund of Geohazard Prevention and Geoenvironment Protection（Grant No.SKLGP2013K012）.

References

Chai JR,Wu YQ.Analysis of seepage forces acting on single-fissure walls.Journal of Engineering Geology 2001；9（1）：29-31（in Chinese）.

Chen H.Controlling factors of hazardous debris flow in Taiwan.Quaternary International 2006b；147（1）：3-15.

Chen HX,Zhang LM,Chang DS,Zhang S.Mechanisms and runout characteristics of the rainfall-triggered debris flow in Xiaojiagou in Sichuan Province,China. Natural Hazards 2012；62（3）：1037-57.

Chen XQ.Experiment of initiation mechanism of landslide translation to debris flow.Chengdu：Southwest Jiaotong University；2006a.p.38-77（in Chinese）.

Cui P.Experimental study on the mechanism and condition of starting up of debris flow.Chinese Science Bulletin 1991；36（21）：1650-2（in Chinese）.

Guo XJ,Cui P,Li Y.Debris flow warning threshold based on antecedent rainfall：a case study in Jiangjia Ravine,Yunnan,China.Journal of Mountain Science 2013；10（2）：305-14.

Hu MJ,Wang R.Testing study on the correlation among landslide,debris flow and rainfall in Jiangjia Valley.Chinese Journal of Rock Mechanics and Engineering 2003；22（5）：824-8（in Chinese）.

Hu MJ.Self-organized criticality and disaster mechanism of debris flow accumulation body.Wuhan：Institute of Rock and Soil Mechanics,Chinese Academy of Sciences；2008.p.62-7（in Chinese）.

Hutchinson JN,Bhandari RK.Undrained loading,a fundamental mechanism of mudslide and other mass movements.Geotechnique 1971；21（4）：353-8.

Iverson RM,LaHusen RG.Dynamic pore-pressure fluctuations in rapidly shearing granular materials.Science 1989；246：797-9.

Kotarba A.Formation of high-mountain talus slopes related to debris-flow activity in the High-Tatra Mountains.Permafrost and Periglacial Processes 1997；8（2）：191-204.

Li F,Guo YC.Analysis of mechanism of rainfall infiltration to slope stability.Yellow River 2007；29（6）：44-5（in Chinese）.

Liu XL,Lu XJ,Su PC.Characteristics and hazard assessment of debris flow in Chayuan Gully of Wenchuan County in Sichuan.Journal of Natural Disasters 2004；13（1）：66-71（in Chinese）.

Ni HY.Experimental study on initiation of gully-type debris flow based on artificial rainfall and channel runoff.Environmental Earth Science 2015；73：6213-27.

Wang J,Yu Y,Pan HL,Qiao C,Ou GQ.Debris flow formation process and critical hydrodynamic conditions in the meizoseismal area of the Wenchuan earthquake.Journal of Mountain Science 2015；12（3）：699-710.

Xu YN,Cao YB,Zhang JH,Chen HQ,Yang M,Wang XW.Research on starting of mine debris flow based on artificial simulation experiment in Xiaoqinling gold ore area.Chinese Journal of Rock Mechanics and Engineering 2009；28（7）：1388-95（in Chinese）.

Xu YN,Kuang SF,Huang YJ,Wang L.Hazard-deciding indices for convergence of debris flow.Journal of Natural Disaster 2002；11（3）：33-8（in Chinese）.

Zhang DJ,Bai SW.Influence of seepage forces on fractured rock slope.West-China Exploration Engineering 2003；2：4-6（in Chinese）.

Zhang LL,Zhang J,Zhang LM,Tang WH.Stability analysis of rainfall-induced slope failures：a review.Geotechnical Engineering 2011；164（5）：299-316.

Zhou JW,Cui P,Yang XG,Su ZM,Guo XJ.Debris flows introduced in landslide deposits under rainfall conditions：the case of Wenjiagou gully.Journal of Mountain Science 2013；10（2）：249-60.

Dr.Yong Wu is an associate professor and doctoral supervisor in Institute of Mountain Hazards and Environment,Chinese Academy of Sciences（CAS）.He is mainly engaged in the study of the mechanism and treatment technology of landslide,rockfall and debris flow since 2005 when he graduated from University of Chinese Academy of Sciences.Dr.Wu has managed over 4 projects as PI that are funded by the National Natural Science Foundation of China,the West Light Foundation of the CAS,the Key laboratory Project Fund of Mountain Hazards and Earth Surface Process,the State Key Laboratory Project Fund of Geohazard Prevention and Geoenvironment Protection,and so on.Moreover,he participated as a key member in more than 10 projects.To date,Dr.Wu is the author and coauthor of more than 50 journal papers and 2 books.In addition,he received 5 patents.

23 March 2015

*Corresponding author.Tel.：+86 15928074439.

E-mail address：wyhongyu@163.com（Y.Wu）.

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http：//dx.doi.org/10.1016/j.jrmge.2015.09.003