基于改进遗传算法的云仿真资源分配算法

包长均

摘 要：近年来，云仿真技术作为一种新型网络化建模与仿真模式受到广泛关注，合理配置仿真资源已成为云仿真技术的核心问题之一。针对传统仿真系统资源分配中存在的资源重用性低、部署难度大等问题，提出一种改进遗传算法来求解仿真模型与虚拟机之间最优映射的算法。实验结果表明，该算法是云仿真运行环境下的一种有效资源调度算法。

关键词：云仿真；虚拟化；资源分配；遗传算法

DOIDOI：10.11907/rjdk.1511009

中图分类号：TP312

文献标识码：A 文章编号文章编号：16727800（2015）009007105

0 引言

在分布式计算、并行计算和网格计算逐步发展成熟的基础上，云计算应运而生。 云计算的核心思想是将计算服务器、存储服务器和宽带等资源通过网络连接，形成以“云”形式统一管理，用户只需根据自身需求请求资源池资源，由云计算中心负责所有资源调度和管理，保证用户能够根据需要获取计算力、存储空间和各种软件服务[1]。

李伯虎院士[2]通过引入“云计算”理念，首先提出构建新网络化建模与仿真平台——“云仿真平台”。云仿真平台通过在虚拟机中部署仿真软件、服务、模型等资源组件，为用户仿真需求提供相应的计算资源。类似于云计算服务模式，云仿真技术将仿真模型、仿真流程等资源接入到云计算环境中，通过仿真模型即服务或仿真流程即服务模式满足用户仿真需求[3]。

随着云计算网络的不断增大和仿真用户不断增多，如何及时、高效对云仿真资源进行调度，提高资源利用率，成为云仿真平台研究的核心问题之一。本文探讨基于遗传算法的云仿真平台资源服务调度技术。

云计算服务中的资源调度技术日渐成为学者关注的焦点。针对仿真资源最优化问题，以往研究中提出了很多有价值解决方案。

文献[4]提出了基于Shapley值的虚拟化资源分配策略，该理论的基础是合作博弈论，该方法高效地实现了虚拟化资源分配。 针对资源分配中的利用率问题，文献[5]提出了基于分类挖掘的网格资源分配算法，通过分类减少资源重新分配次数，提高资源利用效率。 Prodan等[6]

提出了基于连续双向拍卖机制的资源调度方法，该方法同时兼顾了用户和服务提供商的双方利益；

Martino[7]介绍了一种基于遗传算法的网格资源调度算法，在花费一定能耗代价后，能尽可能提高网格资源使用率和负载均衡能力。文献[8]针对云计算的编程模型框架，提出了一种具有双适应度遗传算法，用于解决云计算模型中的资源分配最优化问题，该算法不仅能得到总任务完成时间较短的调度结果，而且此调度结果任务平均完成时间也较短。文献[9]在充分考虑云计算环境动态异构性和大规模任务处理特性的基础上提出了一种改进遗传算法，并通过实验验证该算法能较好地适用于云计算环境中的大规模任务资源调度。 以上文献提出的各种算法都可为本文提供借鉴意义，但是本文所提出问题情境、问题模型与上述研究均不所相同。

1 仿真运行环境动态构建中遗传算法应用

1.1 问题提出

本文研究仿真运行环境构建3层映射模型[2]，如图1所示。构建仿真运行环境，分步将仿真模型动态部署到虚拟机，将虚拟机部署到物理机，并分别实现N：1映射关系。 由于虚拟机与物理机两者之间的映射过程（第二步）与仿真模型和虚拟机两者之间的映射过程（第一步）基本相同，只是获取虚拟机与物理机最优映射约束条件略有不同，因此本文对第二步不作讨论，只探讨仿真模型与虚拟机之间的映射最优化问题。

针对仿真模型与虚拟机之间最优化映射问题，关键是如何将与仿真任务有关的仿真模型映射到不等量虚拟机中，以保证提供的运行环境能满足仿真模型的解算和通讯需求，并且使仿真任务执行效率达到最优。

图1 仿真运行环境的三层构建模型

1.2 问题数学模型及形式化定义

为方便研究，本文将仿真模型性能需求和虚拟机提供性能配置折算为计算性能和通信性能[1]，并分别用Wworkload和Wcom表示。 计算性能由节点计算能力和内存大小决定，而通信性能受限于网络带宽和网络延迟。如式（1）所示：

根据仿真模型与虚拟机数量的大小关系又有不同映射：（1）若仿真模型数量小于或等于虚拟机数量，则在给虚拟机分配仿真模型时，将一个虚拟机上所有资源都占满再去分配其它虚拟机，直到将所有满足其计算需求和通信需求的仿真任务分配完毕，这样得到的映射关系使多个虚拟机上是没有仿真模型，通过关闭没有仿真任务的虚拟机，从而达到节约能耗的目的。 该分配方式简单易操作，本文不再赘述。 （2）若仿真模型数量大于虚拟机数量，则可以采用本节所介绍的映射模型，根据该方法得到的仿真模型到虚拟机间的映射，使得每台虚拟机资源最大使用率最小，进而使整个系统具有更大的灵活性。 下面介绍遗传算法以实现本节中所提出的映射模型。

2 改进遗传算法求解最优映射

遗传算法（Genetic Algorithm， GA）是美国Michigan大学J.H.Holland教授于1975年受Darwin进化论思想的启发而提出。 其核心思想是生物进化过程从简单到复杂、从低级到高级，这本身就是稳健适应自然、适者生存的优化过程。 相较于传统穷举法、微分法等优化算法，遗传算法不仅具有自组织、自适应、自学习的特性，而且具有高鲁棒性和广泛适用性，能突破问题性质限制，有效处理传统优化算法难以解决的复杂问题。 遗传算法的主要优势在于是一种全局优化算法。 搜索空间是问题解的结合，因而其搜索覆盖面更大，范围更广，并能进行多点并行搜索，使得遗传算法能同时对多个解进行处理、评估，搜索广度和随机性更优，能避免陷入局部某个单峰最优解，同时有利于较快收敛到全局最优解。

2.1 染色体编码方式

遗传算法中的染色体编码有很多种，如采用对任务执行状态的直接编码和间接编码。本文采用二进制染色体编码方式：M个仿真模型和N个虚拟机，M个仿真模型对应M个表示单元，而每个表示单元由若干个二进制位表示；每个表示单元的二进制位数k由虚拟机数量N决定，即2k-1

2.2 初始种群生成

由上节可知，本文染色体表示仿真模型到虚拟机的映射。 每一个染色体是一种仿真模型与虚拟机的映射方式，且每一个染色体表示一个种群中的个体。 本文初始种群为随机生成，初始种群数量设为Num。 算法是在这Num个种群中进行选择、交叉、变异，从而生成种群下一代。

2.3 适应度函数

遗传算法是通过适应度函数值进行下一代的选择，从而寻找问题最优解。 因此，适应度函数选取相当重要，关系到算法收敛速度与所得解的优劣。 根据问题模型，要想达到仿真模型与虚拟机之间的最优映射，则必须满足目标函数，遗传算法适应度函数：

f（x）=max（v_cpu[x][j]，v_com[x][j][k]）∑Numi=1max（v_cpu[i][j]，v_com[i][j][k]）（6）

其中，二维数组v_cpu[x][j]表示x号染色体中j号虚拟机计算资源的使用率； 三维数组v_com[x][j][k]表示x号染色体上虚拟机j和虚拟机k上已经部署的仿真模型之间通信量之和占虚拟机j与虚拟机k通信总量的比例。 适应度函数值越小，映射性能越优，越容易被选择。

2.4 选择、交叉、变异操作

2.4.1 选择

在遗传算法中需对种群中的个体按照一定比例进行选择，该比例由适应度函数值决定，选择的目的是将拥有更好基因的个体直接遗传到下一代或将通过配对交叉产生的新个体遗传到下一代。 本文使用轮盘赌选择方式将优秀个体挑选出来，通过适应度值计算出每个个体的选择概率：

ps（i）=1-f（i）∑Numj=1（1-f（j））（7）

其中，f（i）表示第i个染色体的适应度值，ps（i）即为i号染色体被选择的概率。

2.4.2 交叉

交叉是遗传算法中最主要的搜索算子，其模仿自然界有性繁殖基因重组过程，将原有优良基因遗传给下一代个体，并生成包含更优良基因结构的新个体。 交叉是产生后代并区别于父代的主要方式，其以较大概率选择两个个体进行基因位交换，交换后子代既保留了父代大部分基因，也具有自己新的基因特色，整个种群基因会发生相应改变，从而保证种群向最优化方向发展。

2.4.3 变异

所谓变异，是指将基因座上特定值进行改变。当遗传算法通过交叉算子已经接近最优解时，利用变异可以加速种群向最优解收敛。 变异算子pm通常在0.000 1～0.1间取值，适当取值可保持种群多样性，同时防止未成熟收敛现象。本文所述遗传算法变异操作是对种群中的每个个体以pm的变异概率检查其是否发生变异，对进行变异的个体随机选择变异位并改变变异位的值。

2.5 算法终止条件

本文采用的终止条件包括进化的代数G和阈值r，一旦算法执行的进化代数达到G次或在下一代所得到的δ（d）与上一代计算得到的δ（d）的差值小于r时，算法均终止。 此时得到的结果是最优解或趋近于最优解。最优解种群中对应的max（v_cpu[x][j]，v_com[x][j][k]）为最小的染色体，即为最优映射。

2.6 模拟退火算法引入

模拟退火算法思想最先由Metropolis等于1953年提出，并在1983年被Kirkpatrick等成功引入组合优化领域。 模拟退火算法可以看作一个物理模拟过程：从某个较高初始温度出发，先将固体加热至高温状态，此时固体分子间不断发生碰撞，呈无序状态，具有较高的内能； 然后让高温固体慢慢冷却，固体分子将随着热运动的逐渐减弱而恢复到稳定、有序状态。在这个过程中，固体内部粒子在每个温度下都能达到平衡态，最终在常温时达到基态[10]。 模拟退火算法采用Metropolis接受准则能避免过早达到局部最优范围，从而保证所求解的质量。 该接受准则是指当固体处于较高温度状态时，接受新状态可能性较大，而当固体处于较低温度状态时，接受新状态可能性随之降低。最终，当温度趋于0时，任何使内能小于0的新状态都不能被接受。

经典遗传算法的早熟现象是指算法过早陷入局部最优，很难跳出局部走向全局最优。已有研究表明，由于群体规模限制，当该种群进化若干代后，具有较高平均适应度的指数级增长模式将在种群中占有绝对优势，也就是在自然界优胜劣汰中占据统治地位。 如果不加以调整控制，算法中的选择、交叉、变异操作将逐渐因为种群高度一致性而失去作用，整个种群的模式种类将越来越单一，最终导致算法陷入局部最优解[11]。 将模拟退火算法引入遗传算法中，既能避免遗传算法存在的“早熟”问题，大大降低遗传算法陷入局部最优解的可能性，又能增强算法全局收敛特性，提高算法收敛速度。

因此，首先采用遗传算法框架进行最优化问题求解，再引入模拟退火算法优化遗传算法中选择下一代种群的操作，根据Metropolis接受准则以一定概率接受坏解，从而在进化过程中保持种群多样性，最终得到最优解。

2.6.1 Metropolis接受准则

设当前状态下温度值为T，根据粒子当前所处的相对位置，设固体初始状态为i，对应内能为Ei；随后随机选取其中的某个粒子，按随机产生的偏移向量使粒子发生偏移，设偏移后的状态为j，此时内能为Ej。 若Ejβ ，则接受该新状态，否则拒绝改变状态。 通过重复上述过程，系统能量将逐渐降低，最终达到平衡状态。

2.6.2 模拟退火算法参数

（1）温度控制初始值t0。该值选取不宜过大或过小。过大的选择将导致退火算法收敛缓慢，失去可操作性；过小的选择会导致退火算法陷入局部搜索。

（2）温度控制终值tf。该值决定模拟退火算法终止条件，即温度达到某个充分小的值表明算法收敛到某个近似解。本文采取判断算法求解的近似性决定是否终止，若迭代若干次后得到的解没有变化，说明算法解的质量无法进一步提高，从而宣告算法终止。

（3）温度衰减函数f（tk） 。本文取一种常用的衰减函数f（tk）：tk+1=μtk，u∈[0.5，1）。

2.6.3 改进遗传算法流程

本文提出的SAGA算法（Simulated Annealing Genetic Algorithm）分两个阶段：在遗传操作阶段，利用选择、交叉和变异过程对初始种群Gi 进行遗传操作，产生进化后的种群i；在模拟退火操作阶段，将种群i作为输入，釆用模拟退火操作，通过Metropolis准则对i中的个体进行筛选，产生新一代种群Gi+1。具体操作步骤如下：Step 1：初始化种群。 根据仿真模型与虚拟机的数量采用随机方式生成初始种群，初始种群规模记作Mg。 设定进化迭代参数i为0；

Step 2：计算目标函数与自适应函数。首先计算当前种群适应度函数f（i）和最优映射值δ（d）；

Step 3：终止条件判断。 当进化代数达到预定最大进化代数或在下一代所得到的δ（d）与上一代计算得到的δ（d）差值小于r时算法终止，输出搜索结果，否则继续执行；

Step 4：选择操作。 采用轮盘赌法对种群进行选择操作，根据式（7）得到的ps概率来选择适应性较强的个体，形成新群体，进行下一步交叉操作；

Step 5：交叉操作。釆用交叉方法，从经过选择操作产生的群体中随机选择2个个体进行交叉操作，产生2个新个体；

Step 6：变异操作。釆用变异操作方法对被选中个体进行变异操作，将符合要求的新个体放入种群；

Step 7：在温度ti下，计算遗传操作后种群中每个个体的适应度值；

Step 8：根据适应度函数和Metropolis接受准则，判断是否接受当前遗传算法产生的新个体；

Step 9：更新进化迭代计数i=i+l，转到Step 2。

3 实验测试

CloudSim是一款云计算仿真工具，是用于实现对云计算基础设施和应用服务进行模拟的开源框架。 本文使用CloudSim中的DataCenterBroker方法实现算法调度策略。

3.1 实验条件设定

算法参数设置如表1所示。本实验中仿真模型数量取值为1k、2k、3k、4k、5k，逐渐增大。 虚拟机数量设为500。 仿真模型计算资源需求量取值范围为[1，20]，数值越大表示对计算资源的需求越大。虚拟机可以提供的计算资源取值范围为[100，300]。 设仿真模型间所需通信性能取值范围为[1，20]，虚拟机间可用通信性能取值范围为[100，300]。 限定任何一个虚拟机上面部署的仿真模型计算资源需求量之和都不能超过此虚拟机提供的计算资源。

3.2 与经典算法对比

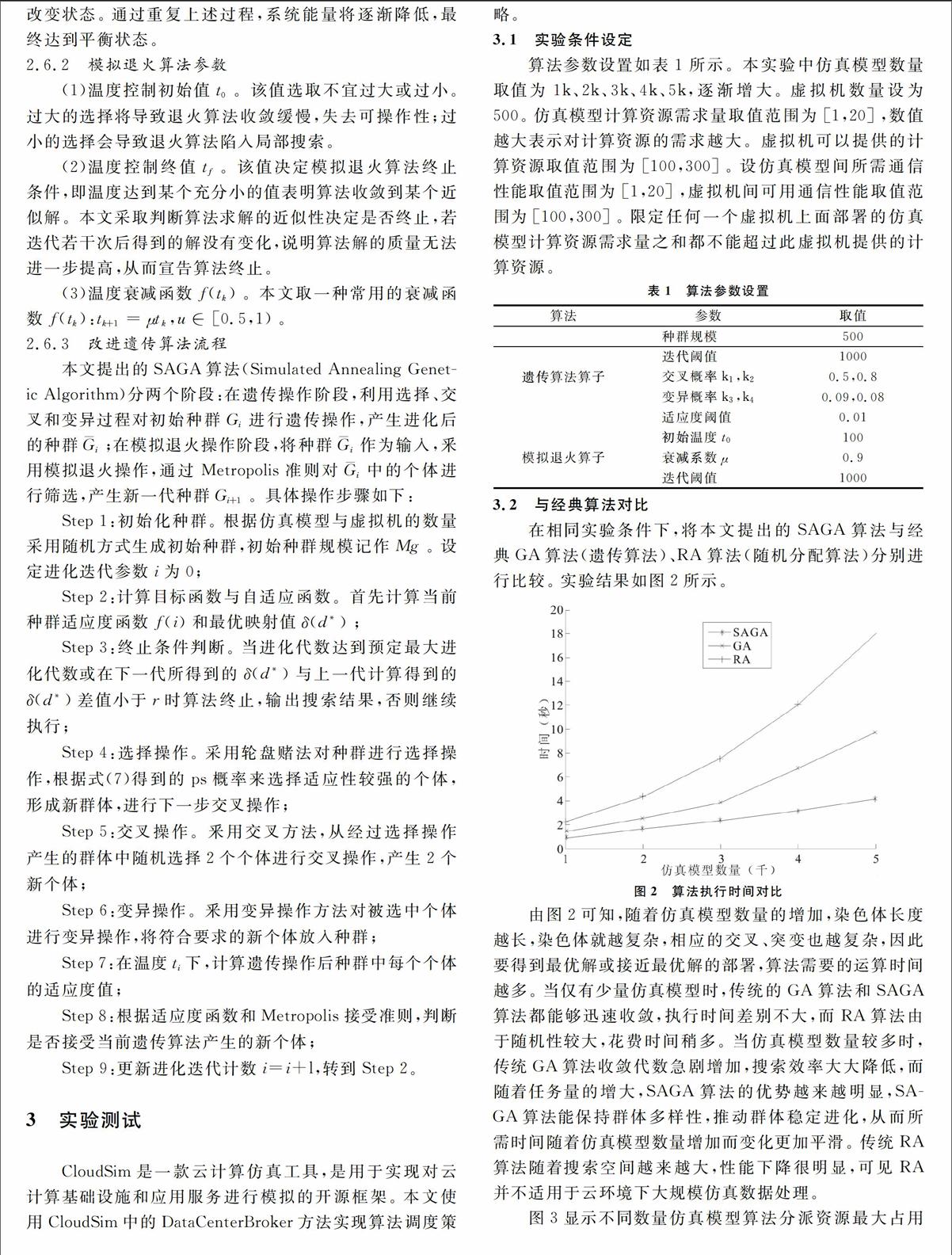
在相同实验条件下，将本文提出的SAGA算法与经典GA算法（遗传算法）、RA算法（随机分配算法）分别进行比较。 实验结果如图2所示。

图2 算法执行时间对比

由图2可知，随着仿真模型数量的增加，染色体长度越长，染色体就越复杂，相应的交叉、突变也越复杂，因此要得到最优解或接近最优解的部署，算法需要的运算时间越多。 当仅有少量仿真模型时，传统的GA算法和SAGA算法都能够迅速收敛，执行时间差别不大，而RA算法由于随机性较大，花费时间稍多。 当仿真模型数量较多时，传统GA算法收敛代数急剧增加，搜索效率大大降低，而随着任务量的增大，SAGA算法的优势越来越明显，SAGA算法能保持群体多样性，推动群体稳定进化，从而所需时间随着仿真模型数量增加而变化更加平滑。 传统RA算法随着搜索空间越来越大，性能下降很明显，可见RA并不适用于云环境下大规模仿真数据处理。

图3显示不同数量仿真模型算法分派资源最大占用率，该值越小则算法性能越优。 总体而言，随着仿真模型增多，3种算法计算资源最大占用率都在增大，RA算法由于采取完全随机分配策略，在仿真模型不断增多后表现最差，最后一组实验资源利用率已近90%，负载提升空间不大。GA算法和SAGA算法都表现出能根据虚拟机运算能力合理分配资源特性，算法倾向于使计算能力强的虚拟机分配到更多任务。虽然传统GA算法在问题规模较小时性能较好，但容易陷入局部最优解，反而导致性能下降。本文提出SAGA算法能有效避免算法早熟，随着资源利用率提升，能够提供更好负载均衡效果。

图3 算法资源最大占用率对比

4 结语

随着大数据时代到来，传统仿真技术越来越难以满足日益复杂的用户仿真需求，而云仿真技术采用云计算理念能够很好地解决这一问题。 针对云仿真运行环境资源分配最优化问题，本文提出了基于改进遗传算法的求解方法，该算法综合考虑了计算性能、通信性能、机器负载等因素。 实验证明，该算法在任务完成时间和负载均衡方面均表现出很强的优势，能较好地适用于云计算环境中大规模仿真任务资源调度。

参考文献参考文献：

[1] 刘鹏.云计算的定义和特点[EB/OL].http：//www.chinacloud.cn/show.aspx？cid=17&id=741.

[2] 李伯虎，柴旭东，侯宝存，等.一种基于云计算理念的网络化建模与仿真平台——”云仿真平台”[J].系统仿真学报，2009，21（17）：52925299.

[3] 胡春生，许承东，张鹏飞，等.云计算环境下仿真模型资源虚拟化研究[J].华中科技大学学报，2012，40（1）：135140.

[4] 张小庆，李春林，钱琼芬，等.基于合作博弈的虚拟化资源效用分配策略[J].计算机科学，2012，39（6）：5153.

[5] 刘林东.基于分类挖掘的网格资源分配研究[J].计算机应用研究，2013，30（2）：371373.

[6] PRODAN R，WIECZOREK M，FARD H M.Double auctionbased scheduling of scientific applications in distributed grid and cloud environments[J].Journal of Grid Computing，2011，9（4）：531548.

[7] DI MARTINO V，MILILOTTI M.Sub optimal scheduling in a grid using genetic algorithms[J].Parallel Computing，2004，30（5）：553565.

[8] 李建锋，彭舰.云计算环境下基于改进遗传算法的任务调度算法[J].计算机应用，2011，31（1）：184186.

[9] 刘愉，赵志文.云计算环境中优化遗传算法的资源调度策略[J].北京师范大学学报：自然科学版，2012，48（4）：378383.

[10] 庞峰.模拟退火算法的原理及算法在优化问题上的应用[D].长春市：吉林大学，2006.

[11] 付旭辉，康玲.遗传算法的早熟问题探究[J].华中科技大学学报：自然科学版，2003，31（7）：5354.

[12] ZHANG Y B，CHAI X D，HOU B C，et al.Research on virtual simulation resource modeling in cloud simulation[C].Proc.of the International Conference on Information Security and Artificial Intellignce，2010：394398.

责任编辑（责任编辑：陈福时）