基于增量式决策树的时间序列分类算法研究

王树英，王志海

（北京交通大学计算机与信息技术学院，北京　100044）

基于增量式决策树的时间序列分类算法研究

王树英，王志海

（北京交通大学计算机与信息技术学院，北京100044）

1　问题的定义

近几年来，数据挖掘技术已经应用到很多研究领域中，时间序列数据也得到越来越广泛的关注，例如股票交易数据、医学脑电波数据、经济销售预测数据、字迹识别数据以及人体姿势数据等。所有这些数据都有一个共同的特征，那就是数据本身是有顺序相关的，且都是实值型数据，定义具有这样特征的数据为时间序列数据。

主要针对时间序列数据维度高、实值有序、数据间存在自相关性［1］等特点，以及大数据理论的发展趋势，提出了一种增量式的时间序列数据挖掘算法。这一部分主要描述时间序列分类涉及到的符号、定义及公式。表1总结了本文中出现的关于时间序列分类的相关记号。

下面，主要讲述关于本文中出现的一些定义。当然，这里假定所有的分类问题都是两类分类问题，多类分类问题是可以实现，只是有些繁琐，这里为了简便起见，只考虑了两类相关的问题。

定义1 时间序列：一条时间序列是T=t1，…，tm，一个具有m个实值变量的有序集合。数据点t1，…，tm是相等时间间隔内数据的有序排列。

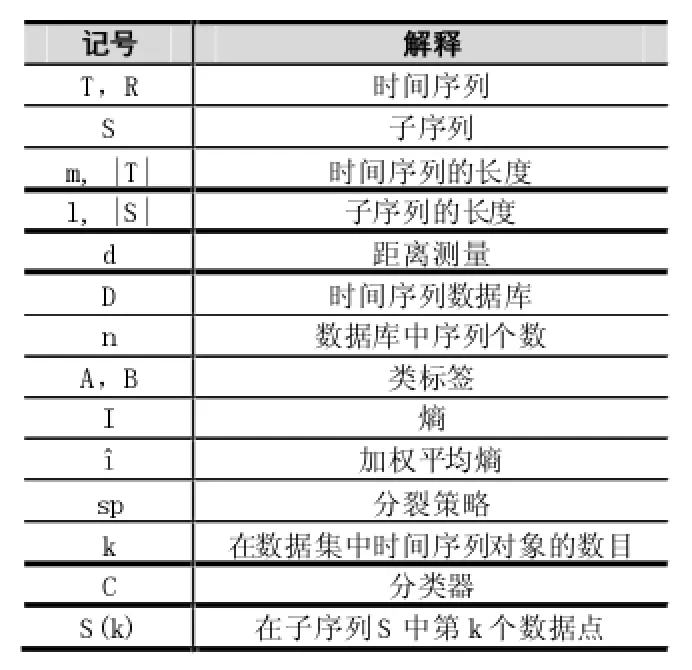
表1　时间序列有关符号

定义2时间子序列：假定一条时间序列T的长度为m，时间序列T的子序列S是一条从T中长度1≤m的连续位置的序列，即S=tp，…，tp+l-1，其中1≤p≤m-l+1。

定义3滑动窗口：给定一条长度为m的时间序列T，以及一个用户定义的长度l，所有的子序列为一个长度为l的滑动窗口通过T之后所得到的。并且我们定义时间序列T的每一个长度l的子序列为Slp，其中上标l为子序列的长度，下标p表示的是滑动窗口在时间序列T中的位置。从时间序列T中获取的所有长度为l的时间序列子序列定义为SlT，其中SlT=｛Slp，1≤p≤ml+1｝。

定义4时间序列之间的距离：距离函数Dist（T，R）表示输入为两条具有相同长度的时间序列T和R，输出为非负值d，即两条时间序列之间的距离［2］。且由函数我们知道，距离公式具有对称性，即Dist（T，R）= Dist（R，T）。

定义5时间序列到子序列之间的距离：函数SubsequenceDist（T，S）用于定义时间序列T与子序列S之间的距离，其中输入为时间序列T和子序列S，输出为非负值d，即两条时间序列之间的距离，如公式（1）所示。

SubsquenceDist（T，S）=min（Dist（S，S'）），

从公式（1）可以看出，时间序列T与子序列S之间的距离为两个序列之间的最小距离。另外，可能需要一些度量标准来分裂数据集，传统的决策树中的信息增益即为典型的例子。

定义6熵：一个时间序列数据集D共有两个类A 和B，假定数据集D中属于类A的对象比例为P（A），属于类B的对象比例为P（B），则熵的定义如公式（2）所示。

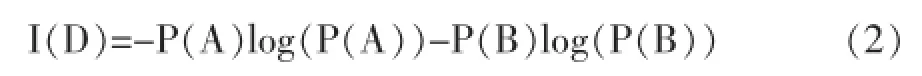
每一种分裂策略将整个数据集D分裂为两个数据集D1和D2，那么分裂之后保留在整个数据集D上的信息，使用每一个分裂子集的加权平均熵定义。假定数据集D1占总体的比例为f（D1），数据集D2占总体的比例为f（D2），则分裂之后数据集D的整体熵如公式（3）所示。

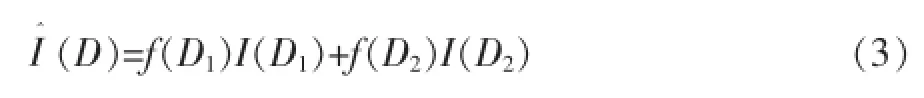
定义7信息增益：给定一个分裂策略sp将数据集D分裂为两个数据集D1和D2，分裂之前和之后的熵记为和，那么基于此分裂策略sp的信息增益如公式（4）所示。

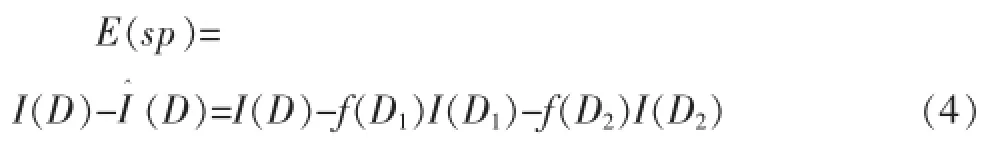
对于基于决策树的时间序列分类问题，主要考虑到时间序列数据维度高、自相关性以及连续数据的特点，提出了一种基于增量式决策树的时间序列分类算法。

2　基于决策树的时间序列分类

正如基本决策树理论所描述，它采用了一种分而治之的策略，而且算法本身具有可解释性。在此基础上，提出了一种发现shapelet的过程，即发现一条时间序列中最具代表性的时间序列［3］。事实上，这个过程需要很大的存储空间去存储候选集的相关信息，能够在判断最优shapelet的同时，生成候选集然后删除非最优的候选集，这样就能够节省大量的空间。从另一方面来说，shapelet的方法会产生很大的时间复杂性［4］。假定时间序列shapelet的长度为k，平均每一个时间序列的长度为，那么候选集的空间复杂度为O（2k）。其中搜索每一个候选集需要的时间复杂度为O（k），那么搜索整个候选集的时间复杂度为O（3k2）。

基于上述描述的时间序列分类问题的时间复杂度和空间复杂度，那么提出了两种加速策略：

（1）子序列早期放弃（SDEA）策略

在发现shapelet的过程中，需要全局搜索时间序列数据集。在全局搜索的过程中，涉及到计算候选序列到一条时间序列序列的距离。子序列到一条时间序列序列的距离为子序列到时间序列中相同长度的子序列距离长度最小的那个。那么在计算这个距离的过程中，设置一个参数μ为当前情况下的最小距离。子序列到时间序列的计算过程中，如果发现得到的欧几里得距离小于这个参数 ，那么就可以舍弃这一部分的计算过程，因为当前计算的距离只可能比这个参数μ要大，而子序列到时间序列的距离去最小值即可。

（2）可容许的熵剪枝（AEP）策略

SDTC算法在发现shapelet的过程中需要的时间代价最高，相比之下计算信息增益需要的时间代价非常小。基于这样的考虑，代替计算候选集到所有时间序列的距离，可以计算当前所得距离的信息增益上限。如果shapelet发现过程任意点的信息增益上限小于当前最好的信息增益，可以停止当前距离的计算，并减掉当前正在计算距离的那个候选集，因为可以确定这个候选集不是目前为止最好的候选集。

下面给出SDTC算法的具体算法描述：

输入： 数据集 D，shapelet候选集的最大值MAXLEN、最小值MINLEN

输出：shapelet决策树分类器

//发现 shapelet过程，返回shapelet及最佳分裂距离splitdist

3　基于增量式决策树的时间序列分类

从决策树的构造过程来看，随着样本的增加，并不需要对决策树进行重新构造，而只需要重构与样本相关的子树，大大降低了建树的复杂性［5］。考虑到时间序列数据集实例多且构造决策树的速度慢，本算法在SDTC算法的基础上，结合了增量式学习的思想［6］，可先用部分数据进行训练，然后将剩余部分进行增量学习，继而提出了一种新的基于增量式决策树的时间序列分类算法ISDTC算法。

这里存在一个问题，当有一条新的实例到达训练集时，原先选择的分裂属性的分类能力可能会随着新实例的到达而降低。当候选属性中存在比原先选择的分列属性分类能力更好的属性时，本能就用新的候选集取代原先选择的分类属性。根据定义7信息增益可知，两个属性的信息增益之间的差值比较之后，可以得到如下所示的公式。

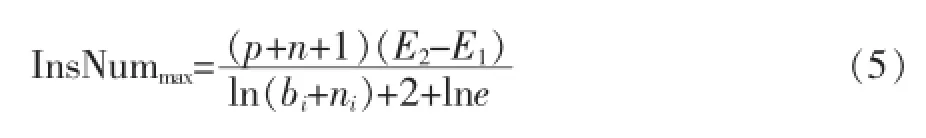
pi和ni分别为分类属性两个值的数目大小，p和n分别为正例和负例的数目。当增加的实例数目小于等于InsNummax时，不需要更新分类属性；当增加的实例数目大于InsNummax时，就需要更新分类属性．在研究增量式时序分类问题时，就是基于此公式来判断是否需要更新分类属性。

ISDTC算法的具体算法描述：

输入：时间序列数据集，shapelet候选集的最大值MAXLEN、最小值MINLEN

输出：增量式决策树

（1）初始化。树型根节点的初始化，指定可以发现shapelet的数据集数目m值，以及记录每条实例信息的结果InsInfo；

（2）判断接收到的实例个数是否达到m值。如果未达到指定的值m，继续接收实例。如果达到m值，运行FindShapeletBF（）找到最好的shapelet，计算到该属性到每条序列的距离，根据距离将数据离散化表示，并计算该shapelet的正例数目和负例数目。

（3）当下一条数据到达时，根据当前的shapelet计算子序列距离并离散化表示，存在下面两种情况：

①如果实际数目小于InsNummax，则继续接收实例；

②如果实际数目大于InsNummax，则说明存在更具可辨别性的子序列shapelet。重新计算shapelet的值，计算到每条时间序列距离并离散化，并以这个属性为分裂点分裂这个数据集。

（4）分裂数据集以后，递归循环2、3过程，直到决策树到达叶节点，最终生成一颗健壮的决策树。

这里需要注意的是，初始化阶段直接指定了需要发现shapelet的数据集数目m的值，可以考虑采用一种动态生成的方式来确定m的值。另外，发现shapelet的过程与分裂数据集的过程，都用了信息论中的熵和信息增益的概念，可以考虑定义一个数据结构记录这些信息增益的基本情况，这样在牺牲一定存储空间的基础上，大大减小了计算上所花费的时间。另外，在发现shapelet的过程中，应该遵循下面一些基本原则：

①发现的shapelet尽可能具有可解释性；

②在信息增益相同的情况，选定的shapelet的长度尽量采用短时间序列，这样会减少计算距离的时间。

4　实验结果分析

4.1实验平台和数据

（1）简要说明进行该实验时涉及到的实验环境，如下所示：

①JDK版本：Java SE Development Kit 7u11 for Windows x86；

②IDE环境：eclipse-standard-luna-R-win32；

③Weka版本：weka-3-7-12 for Windows x86。

（2）实验数据：

为了评价shapelet转化的性能，选择了UCR时间序列数据库中14个数据集，数据集详细信息如表3所示。

4.2实验结果分析

下面对本文提到的两种加速策略以及基于增量式决策树的时间序列分类算法进行详细的结果分析，分析结果如下所示。

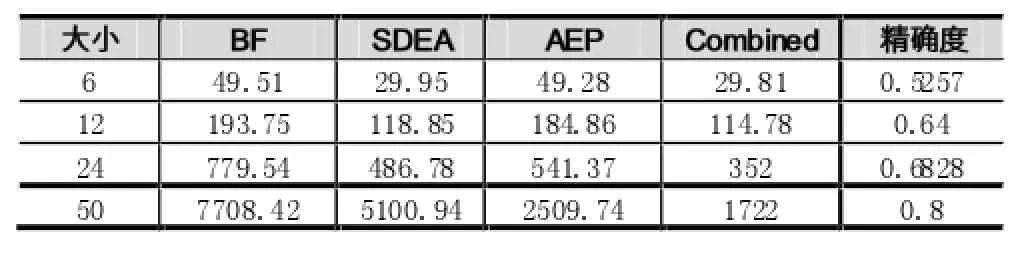
表2　两种加速策略的时间和精确度比较

为了便于比较提出的两种加速技术与相结合后的性能比较，通过图1进行可视化展示。

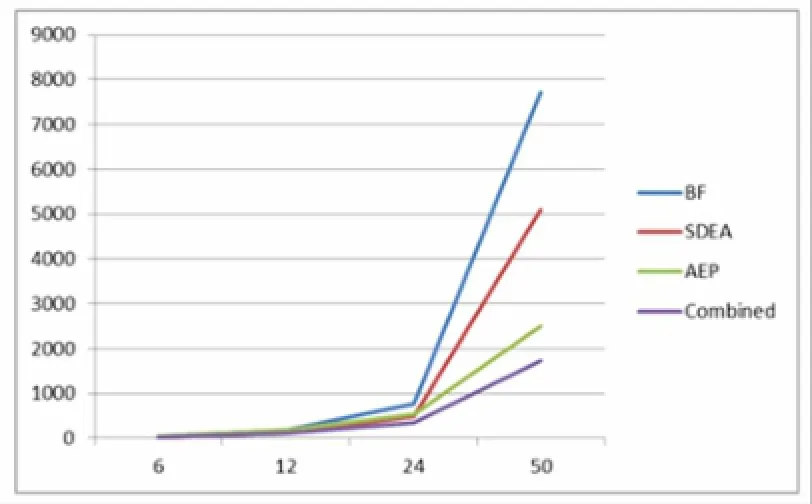
图1　两种加速策略和合并两种策略后的时间比较

针对提出的基于增量式决策树的时间序列分类算法，可以采用比较精确度的方式与决策树的时间序列分类算法进行比较，下面是在14个UCR数据集上进行精确度验证的结果展示。

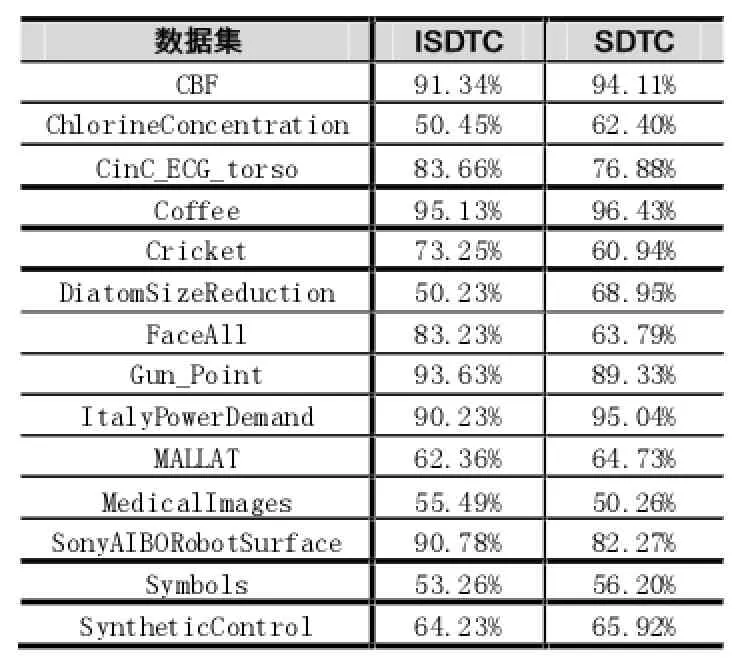
表3　两种时间序列分类算法的精确度比较

为了便于比较ISDTC算法和SDTC算法的准确率，将上述过程展示如图2所示。

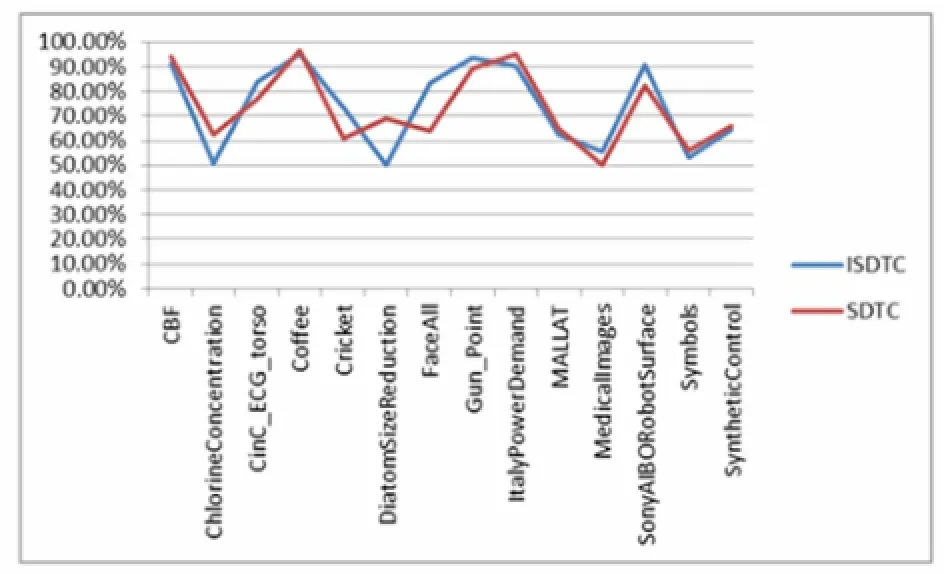
图2　ISDTC算法和SDTC算法的分类精确度比较

从图2可以看出，两种分类方法的分类精确度非常接近，说明提出的基于增量式决策树的时间序列分类算法——ISDTC算法能够产生与使用静态数据进行构建决策树的时间序列分类算法——SDTC算法类似的决策树。当然，事实这种比较方法是不严谨的，但是基于时间序列数据为高维数值型数据，很难可视化表示的特点，本文以比较精确度的方式进行说明。

5　结语

随着数据挖掘技术的广泛研究，复杂数据类型的挖掘得到越来越多研究人员的关注。本文从复杂数据类型中的时间序列数据出发，研究了当前国内外关于时间序列分类的研究现状［7～8］，根据当前大数据的实际以及对时间和空间的要求，以及基于决策树分而治之的测量以及可解释性，提出基于增量式决策树的时间序列分类算法——ISDTC算法。实验表明本文中提出的基于增量式决策树的时间序列分类算法最终生成的增量式决策树，能够产生与在静态数据中进行时间序列分类算法生成的决策树相似精确的决策树。

［1］Esling P，Agon C.Time-series Data Mining［J］.ACM Computing Surveys（CSUR），2012，45（1）:12

［2］Faloutsos C，Ranganathan M，Manolopulos Y.Fast Subsequence Matching in Time-Series Databases.SIGMOD Rec，1994:419～429

［3］Ye L X，Keogh E.Time Series Shapelets:A New Primitive for Data Mining［C］.In:Flach P and Zaki M（eds.）.Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining（KDD2009，Paris，France）.New York:ACM Press，2009：947～956

［4］Ye L，Keogh E.Time Series Shapelets:A Novel Technique that Allows Accurate.Interpretable and Fast Classification.Data Mining and Knowledge Discovery，2011，22（1-2）：149～182

［5］Utgoff P E.An Improved Algorithm for Incremental Induction of Decision Trees［C］.In:Proceedings of the Eleventh International Conference on Machine Learning，1994：318～325

［6］Utgoff P E.Incremental Induction of Decision Trees［J］.Machine Learning，1989，4（2）:161～186

［7］何晓旭.时间序列数据挖掘若干关键问题研究［D］.中国科学技术大学，2014

［8］Hills J，Lines J，Baranauskas E，et al.Classification of Time Series by Shapelet Transformation.Data Mining and Knowledge Discovery. 2013：1～31

Time Series；Incremental Learning；Decision Tree；Algorithm Research

Research on the Time Series Classification Algorithm Based on Incremental Decision-Tree

WANG Shu-ying，WANG Zhi-hai
（School of Computer and Information Technology，Beijing Jiaotong University，Beijing 100044）

1007-1423（2015）08-0026-05

10.3969/j.issn.1007-1423.2015.08.006

王树英（1988-），女，山东人，硕士研究生，研究方向为数据挖掘、模式识别

2015-01-13

2015-02-13

数据挖掘技术已经应用到很多研究领域中，数据挖掘的类型也越来越复杂。其中一类数据本身是有顺序相关的，且是实值型数据，定义具有这样特征的数据为时间序列数据，使用常见的数据挖掘方法从时间序列数据中进行知识学习是不适用的。并且随着大数据理论的不断发展，能够增量式地处理数据以减小对时间和存储空间的需求。基于时间序列数据维度高、实值有序、数据间存在自相关性等特点，提出一种增量式决策树的时间序列分类算法。

时间序列；增量式学习；决策树；算法研究

北京市自然科学基金（No.4142042）

王志海（1963-），男，河南人，博士，教授，研究方向为数据挖掘

Data mining technology has been attracting great interest in a vast array of research areas,and their types are more and more complex. The data is related and ordered set of real valued variables,and then such data with above characters is called time series.The following conclusion is that common method of data mining method can't be suit to time series data mining.And with the continuous development of the theory of big data,incremental method is essential in order to decrease temporal and space demand for implement of time series. Focuses on the research on time series classification according to time series features of high dimensionality,ordered real-valued variables,auto-correlation and so on.And proposes incremental decision-tree algorithm for time series classification.