一种基于节点中心度的社区划分新算法

乔健，杨昆朋

（北京交通大学计算机与信息技术学院，北京　100044）

一种基于节点中心度的社区划分新算法

乔健，杨昆朋

（北京交通大学计算机与信息技术学院，北京100044）

0　引言

人类社会中很多的系统都可以抽象为网络，如人际关系网［1］、论文引征网、科学家合作关系网［2］、微博用户关系网、互联网［3］等。这些网络都具有共同特点，即复杂的内部结构，因此被称为复杂网络。在复杂网络中，每一个节点表示网络中的个体，节点之间的连边表示个体之间的相互关系以及相互作用。已有研究表明：这些网络中包含着一些潜在的社区结构［4］。通常，社区内的节点具有相似的特性，在网络中扮演着相似的角色，通过社区划分来识别网络中的社区结构，有助于我们更深入地理解网络的本质，认识网络结构与其功能之间的关系［5］。目前，社区划分方法已被应用于恐怖组织识别、社会网络分析、蛋白质交互网络分析［6］、Web文档聚类和论文引证网络等各个方面。

由于社区划分就是对网络中的节点进行分组，因此社区划分的本质是一个聚类问题［7］。如果定义了网络中节点之间的相似度，那么就可以使用任意一种聚类算法对网络中的节点进行聚类，从而达到网络社区划分的目的。因此，许多聚类算法都可以用来对网络进行社区划分，如K-means［8］算法、AP［8］、NMF［9］算法等。其中K-means算法是一种受到广泛使用的，最为经典的基于划分的聚类方法，有着效率好、易于理解、算法灵活等优点。

1　K-means基础

K-means算法的基本思想是：以空间中K个点为中心进行聚类，将最靠近它们的节点归类。通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果。

假设要把样本集分为K个簇，算法描述如下：

算法：K-means算法

输入：点集合NodeList，簇的个数K

输出：簇列表CommunityList；

（1）随机选择K个簇的初始中心节点；

（2）在第t次迭代中，对每一个点，求其到K个中心的相似度，将该点归到相似度最大的中心节点所在的簇中；

（3）利用均值等方法更新簇的中心值；

（4）对于所有的K个聚类中心，如果利用步骤（2），（3）的迭代法更新后，这K个聚类中心在某个精度范围内不变化或者达到最大迭代次数，则算法结束，否则重复执行步骤（2）。

K-means算法的时间复杂度为O（tKNd），空间复杂度为O（（d+K）N），其中，t为迭代次数，K为所期望划分的簇的个数，N为节点数，d为特征向量的维度。传统的K-means算法也有很大的缺陷，其划分结果对初始中心节点十分敏感，而随机选取初始中心节点的方法会导致K-means算法划分结果不稳定、度差、划分结果中很容易出现空社团等问题。本文针对K-means算法的上述缺点，提出了一种基于中心度的中心节点选取法的K-means改进算法——CDK（Center Degree K-Means）算法。基本思想是根据节点的中心度（degree centrality）以及节点之间的最短路径来选取初始社团的中心节点。优先选择中心度较大的节点为初始中心点，并且通过节点之间的最短路径来保证各中心节点之间的距离最远。CDK算法保证了划分结果有较高的精确度和稳定性，避免出现空的社团，并且由于使用中心度来刷新中心节点，避免了每次迭代都需要计算质心以及相似度，因此降低了时间复杂。

2　相关定义

给定图G（V，E），V=｛v1，v2，…，vn｝表示图中的节点集合，E⊆｛（vi，vj）|vi，vj∈V｝表示节点之间的链接集合，图G可以用邻接矩阵描述。

定义1邻接矩阵：邻接矩阵描述图中各节点两两之间的关系。邻接矩阵A=｛aij｝的元素aij定义为如果（vi，vj∈V），元素aij=1，否则aij=0。

定义2节点中心度：节点中心度基本思想是重要的节点是那些拥有与其他节点有较多连接边数的节点。一个网络图中节点的重要性可依据它们度分布的大小进行排序。相应的，节点vi的中心度［6］定义如下：

其中D表示节点的度，n表示网络中的节点个数。

定义3节点相似度：节点相似度用来衡量两个节点之间的相似性，来决定它们是否属于同一类别。基于节点邻居信息的Jaccard［11］相似度定义如下：

3　算法提出

节点中心度描述了节点在网络中处于中心的程度。如果网络看做一个社团，那么节点中心度最大的节点应该是社团的中心节点［11］。根据这个思想，我们可以将网络中的节点按照节点中心度进行排序，然后选取中心度最大的节点作为第一个中心节点，而对于其他的中心节点，我们除了要考虑节点自身的中心度之外，还需要考虑节点与其他中心节点的距离，必须要保证中心节点之间的距离尽可能远，这样才能保证社团之间的相似度尽可能小。因此我们可以使用节点之间的最短路径来保证中心节点之间的距离尽可能的远。我们可以使用一个临界值μ，如果候选与已选中心节点的最短路径均大于μ则可以选为新的中心节点，否则放弃该节点。

给定无向连通图G=（V，E），用n，m，K表示G中的节点数、连边数以及社团数。基于中心度的K-means型社团检测算法如下步骤实现：

输入：社团数目K，临界值μ；

输出：网络G的社区划分结构；

（1）排序：对网络中的节点按照中心度大小进行降序排序；

（2）选择初始中心节点：找出网络中中心度最大的节点作为第一个初始节点并加入社团中心点集C；按中心度的顺序迭代网络中的节点，对于节点vi，如果它与C中的节点的最短路径均大于μ则选vi为新的中心节点并且加入C，否则查看下一节点，直至找到K个初始中心节点。

（3）节点划分：迭代网络中的非中心节点，对于节点vi，通过公式（2）计算vi于C中的中心节点的相似度，将vi划分与相似度最大的那个中心点所在的社团中。

（4）刷新中心节点：对每一个社团中的节点按照中心度进行排序，选取当前社团中中心度最大的节点作为新的中心节点。

（5）判断结束条件：比较刷新后得到的中心节点比起上一次的中心节点，如果没有发生变动或者达到算法最大迭代次数T则结束，否则循环执行第（3）步。

4　实验效果展示

为了验证本算法的性能，本文将DCK算法和传统的K-means算法以及GN［6］算法同时应用在Citeseer和Cora网络进行了比较，用ACC、NMI、PWF和Modularity这四个指标来辅助评价划分效果。

假设网络G的社区结构C=｛C1，C2，…，Ck｝表示真实的社区结构，Ck表示第k个社团，Ck中包含一系列节点。C'=｛C1'，C2'，…，Ck'｝表示由一个社区划分算法划分出的社区结构。因此标准化互信息NMI定义如下：

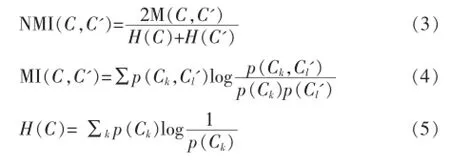
其中p（Ck）表示从网络中随机抽取一个节点，该节点属于社团Ck的概率，p（Ck，Cl'）表示随机抽取的节点属于社团Ck和Cl'的联合概率。

假设T表示在划分C中，属于同一个社区的节点对（i，j）的集合。S表示在划分C'中，属于同一个社区的节点对（i，j）的集合。因此PWF的计算公式定义如下：

其中Npre=|S∩T|/|S|和Nre=|S∩T|/|T|。

假设节点i的真实类标签是si，由划分C分配；ri由划分C'分配的类标签，则划分C'的精确度ACC定义如下：

其中Nset表示网络G的节点集合，δ（x，y）是狄利克雷函数，如果x=y函数值为1，否则为0，|Nset|表示节点个数。

Modularity的定义如下：

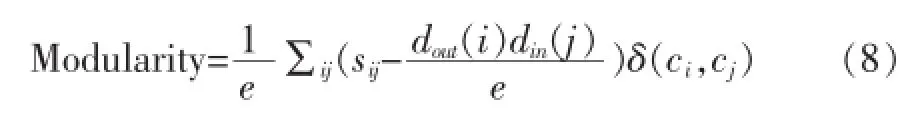
其中dout（i）和din（j）分别表示节点i和j的出度和入度，e表示网络中的有向边的个数，ci表示节点i所在的社团，δ（ci，cj）表示克罗内克函数，Modularity值越大，说明效果越好。

用 Java1.7编写算法程序，在Lenovo ThinkPad T420笔记本电脑上进行了实现。结果如下：

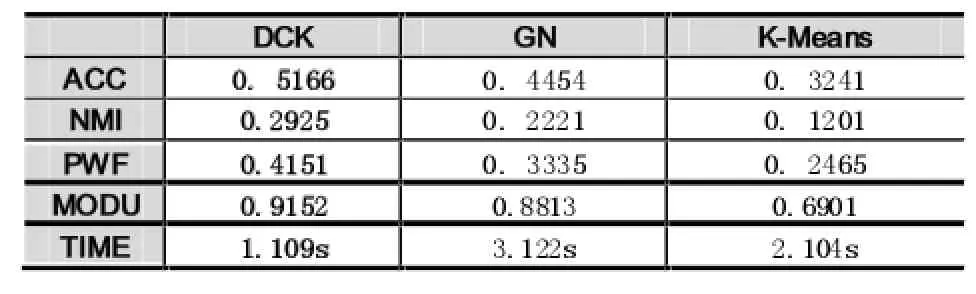
表1　Citeseer数据集各项指标

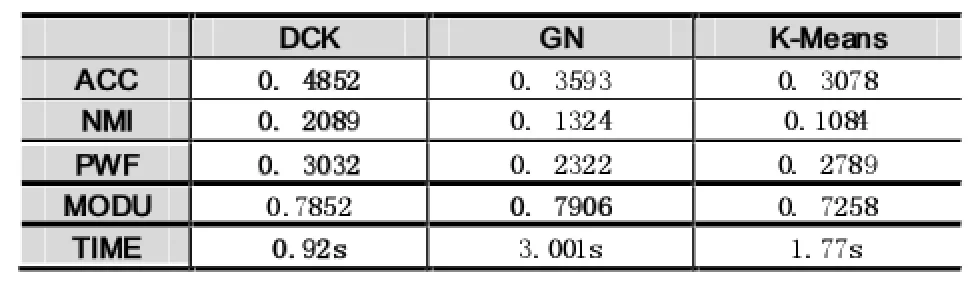
表2　Cora数据集各项指标

由表1和表2的数据，我们可以看出使用DCK算法进行社区划分的精度以及模块度要远远好于K-means算法和GN算法，并且同样的数据DCK算法运行时间要远远小于K-means算法和GN算法。

5　结语

本文给出了一种基于节点中心度的社区划分新算法，该算法利用了节点中心度的思想结合节点间最短路径，通过临界值μ来保证初始中心节点的之间的距离尽可能的远。把该算法应用在Citeseer和Cora数据集上，并与K-means算法和GN算法做了比较，实验表明DCK算法在运行效率和效果上比起传统的K-means算法和GN算法具有明显的优势。但是DCK算法适合于社团特征较为明显的网络，若社团结构不明显，不但社团数K难以确定，对初始中心点的选取也会有一定偏差，如何解决此问题是本文进一步要做的工作。

［1］Amaral LAN，Scala A，Barthelemy M，et al．Classes of Small-World Networks［J］．Proc．Natl.Acad.Sci.USA，2000，97（21）：11149～11152

［2］Redner S．How Popular is Your Paper.An Empirical Study of the Citation Distribution［J］．EurPhys JB，1998，4：131～134

［3］杨博，刘大有，刘继明等．复杂网络聚类方法［J］．软件学报，2009，20（1）：54～66

［4］Watts D J，Strogatz Steven H．Collective Dynamics of Small-World'Networks［J］．Nature，1998,393（6684）：440～442

［5］Albert R，Barabasi A-L.Emergence of Scaling in Random Networks［J］.Scinece，1999，286（5439）：509～512

［6］Girvan M，Newman M E J.Community Structure in Social and Biological Networks［J］.Proc.Natl.Acad.Sci.，2002，99（12）：7821～7826

［7］Yawen Jiang，Caiyan Jia，Jian Yu.An Efficient Community Detection Method Based on Rank Centrality［J］.Physica A，2013，392：2182～2194

［8］J.B.MacQueen.Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability，Berkeley，University of California Press，1：281～297（1967）

［9］Frey B.J.and Dueck D.Science，315，972～976（2007）

［10］C.Ding，X.He，Horst D.Simon，SDM（2004）

［11］Liu Zhi-yuan，Li Peng，Zheng Ya-bin，et al.Community Detection by Affinity Propagation［R］，2008

Degree Centrality；K-means；Community Detecting

New Algorithm of Detecting Community Structure Based on Degree Centrality

QIAO Jian，YANG Kun-peng
（School of Computer and Information Technology，Beijing Jiaotong University，Beijing 100044）

1007-1423（2015）08-0022-04

10.3969/j.issn.1007-1423.2015.08.005

乔健（1984-），男，宁夏固原人，硕士研究生，研究方向为数据挖掘、模式识别

2015-01-15

2015-03-11

针对传统的K-means算法的划分结果受初始中心节点影响较大，以及每次刷新中心节点均需要进行计算，使得算法运行时间较高等问题，提出一种基于中心度的K-means改进算法CDK算法。该算法根据节点的中心度以及节点之间的最短路径来确定初始社团的中心节点，然后根据节点之间的Jaccard相似度，将非中心节点划分到K个社团中。CDK算法避免了传统的K-means算法由于随机选取初始中心点而造成划分结果不稳定、精度较差的问题，同时CDK算法在刷新中心节点的时候无须进行计算，具有更低的时间复杂度。

中心度；K-means；社区发现

杨昆朋（1988-），男，河南邓州人，硕士研究生，研究方向为机器学习、深度学习

Dividing the result for the traditional K-means algorithm is influenced by the initial central node,and each refresh center nodes need to be calculated,cause the higher algorithm running time and other issues.Proposes an improved algorithm based on centrality of K-means, CDK algorithm.The algorithm is based on the shortest path between the node and the node to the center of the central node determining the initial associations,then according to Jaccard similarity between nodes,will be divided into K non-central node in societies.CDK algorithm avoids the traditional K-means algorithm due to the random selection of initial results of the center divide and cause instability, poor accuracy problems,while CDK refresh algorithm when the central node without calculation,has a lower time complexity.