一类脉冲时滞抛物系统的 (全)振动判据
罗李平
(衡阳师范学院数学与统计学院,湖南衡阳 421002)
一类脉冲时滞抛物系统的 (全)振动判据
罗李平
(衡阳师范学院数学与统计学院,湖南衡阳 421002)
研究一类具脉冲扰动和时滞效应的抛物系统的 (全)振动性,借助一阶脉冲时滞微分不等式的某些结果,得到了该类系统在第二类边界条件下所有解 (全)振动的若干充分判据,结论充分表明这种 (全)振动是由于脉冲量和时滞量所引起的。
抛物系统;(全)振动性;脉冲;时滞
0 引言
脉冲是事物在其发展过程中受到瞬时扰动而产生的一种很普遍的现象,在物理学、化学、医学、种群动态学、生态学、生物系统、控制系统、最优化理论以及火箭与航天运动模型中广泛存在。对于这种现象,人们常用脉冲(偏)微分系统来描述,其最突出的特点是能够充分考虑瞬时突变现象对状态的影响,能够更深刻、更精确地反映事物的变化规律。因此,对脉冲(偏)微分系统理论的研究愈来愈引起人们的重视。振动性理论作为脉冲(偏)微分系统定性理论的一个重要分支,也得到了长足的发展,已陆续取得一些很好的研究结果[1-9]。本文受文献[1-2]的启发,研究一类特殊的脉冲时滞抛物系统(1)在第二类边界条件(2)下的(全)振动性问题,直接从(全)振动的定义出发,利用Green散度定理和第二类边界条件把这类系统解的振动问题转化为脉冲时滞微分不等式不存在最终正解的问题,利用二阶脉冲时滞微分不等式的某些结果,建立了判别其所有解(全)振动的若干充分条件,所得结果充分反映了脉冲扰动和时滞效应在系统(全)振动中的决定性作用。所用方法异于通常的垂直相加法。

其中Im={1,2,…,m},I∞={1,2,…},R+=[0,∞],Ω⊂Rn是具有逐片光滑边界ƏΩ的有界区域,Δ是Rn中的n维Laplace算子,N表示ƏΩ的单位外法向量;τij,σi,ρj为正常数,i,j∈Im;0<ti<t2<…<tk<…是固定点列且.
在本文中,对系统(1)我们总假定下列条件成立:
(H1)aij,bij∈PC(R+;R+),i,j∈Im;pi,qi∈PC(R+×;R+),这里PC表示具有如下性质的分片连续函数类:仅在t=tk,k∈I∞,为第一类间断点,但在t=tk左连续;, x)},i∈Im,
(H2)ci∈PC(R+××R2m;R),并且
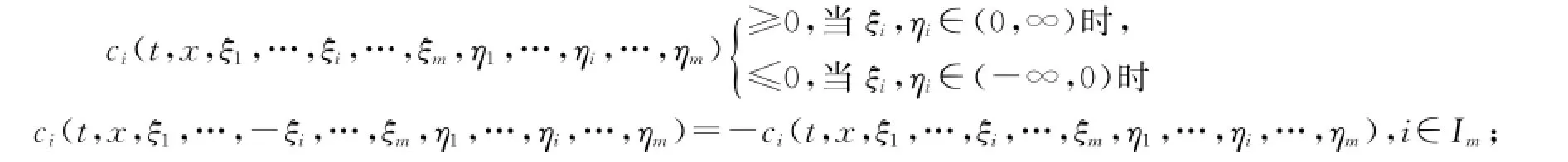
(H3)Ji∶R+ׯΩ×R→R,对任意函数有

且

其中αik>-1为常数,i∈Im,k∈I∞.
定义1 称向量函数u(t,x)=(u1(t,x),u2(t,x),…um(t,x))T为系统(1),(2)的解,若对i∈Im,ui(t,x)满足:
①对固定的x,,ui(t,x)是以tk为第一类间断点的分段连续函数;,k∈I∞,且满足(1)式的第二式;
定义2 称数值函数v(t,x):G→R为非振动的,若它最终为正或最终为负;反之,称v(t,x)为振动的。称向量函数u(t,x):G→Rm为非振动的,若它的每一分量都是非振动的;称向量函数u(t,x):G→Rm为振动的,若它至少有一分量作为数值函数是振动的。称向量函数u(t,x):G→Rm为全振动的,若它的每一个分量作为数值函数都是振动的。
引理1[10]设a(t),b(t)∈(R+,R)是局部可积函数且b(t)≥0;0<t1<t2<…<tk<…且,y(tk);bk>-1,k∈I∞;τ为正常数。若
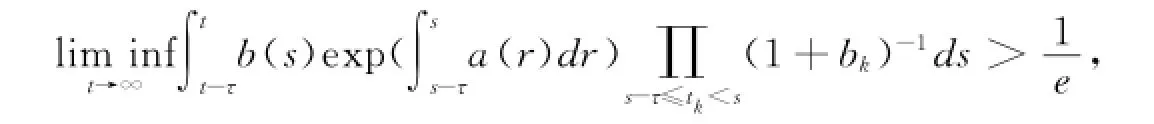
则脉冲时滞微分不等式

无最终正解(参见文[10]中的定理2)。
1 主要结果及其证明
为叙述方便,引入如下记号:

定理1 若对每一个i∈Im,有

则系统(1),(2)的所有非零解在区域G内全振动。
证明(用反证法)假设系统(1),(2)有一个非全振动解u(t,x)=(u1(t,x),u2(t,x),…,um(t,x))T,则)在G内非振动。不失一般性,设ui0(t,x)最终为正,于是存在T>0,使得∀(t,x)∈[T,∞]×Ω,有.
考虑下面的方程:

(Ⅰ)当t≥T,t≠tk,k∈I∞时,对(4)式的第一式两边关于x在Ω上积分,有

由Green公式及边值条件(2)有

其中d S是ƏΩ上的面积元素。
由条件(H3)易知
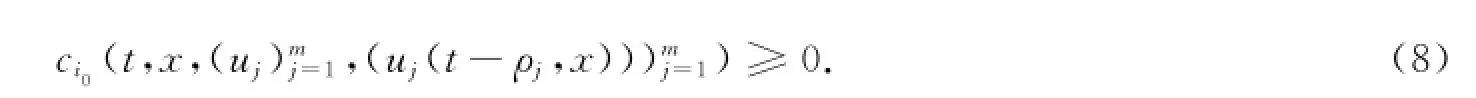
因此由(5)-(8)式及条件(H1)可得
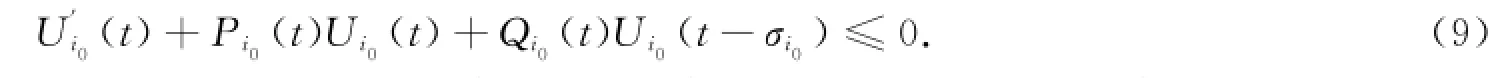
(Ⅱ)当t≥T,t=tk,k∈I∞时,由(4)式中的脉冲条件,结合条件(H4)及定义1中的条件①可得

从而可知脉冲时滞微分不等式(9),(10)有最终正解Ui0(t)。另一方面,结合条件(3),由引理1知,脉冲时滞微分不等式(9),(10)无最终正解,矛盾。
若ui0(t,x)最终为负,令¯ui0(x,t)=-ui0(x,t),¯Ui 0(t)=(x,t)d x。则类似于上面的过程,同样可以得到矛盾。定理1证毕。
仿照上述结果的证明方法,很容易得到下面的关于系统(1),(2)振动的结论。限于篇幅,其证明在此略去。
定理2 若存在某一i0∈Im,使得
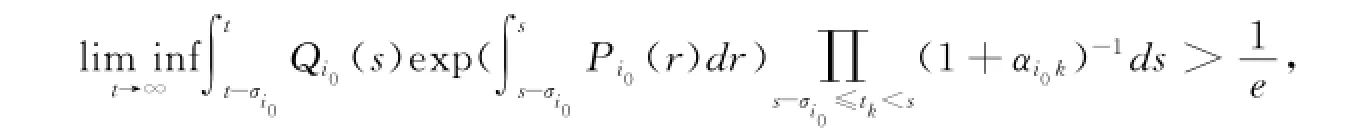
则系统(1),(2)的所有非零解在区域G内振动。
注1 若用下面条件

代替引理1中的极限条件(参见文[10]中的定理3),则还可以得到分别平行于本文定理1、定理2的判别系统(1),(2)所有解(全)振动的新的显式充分条件。
注2本文结果表明,系统(1),(2)的非零解在区域内(全)振动与脉冲量和时滞量有关。
注3由本文结果易知,若系统(1),(2)全振动,则系统(1),(2)必振动。
[1]罗李平,罗振国,曾云辉.带脉冲效应的拟线性双曲系统(强)振动性分析[J].山东大学学报:理学版,2015,50(3):57-61,66.
[2]罗李平,曾云辉,罗振国.具脉冲和时滞效应的拟线性双曲系统的振动性定理[J].应用数学学报,2014,37(5):824-834.
[3]罗李平,曾云辉,罗振国.具脉冲效应的非线性时滞抛物系统的振动分析[J].吉林大学学报:理学版,2014,52(6):1131-1135.
[4]罗李平,罗振国,曾云辉.基于脉冲控制的非线性时滞双曲系统的振动分析[J].系统科学与数学,2013,33(9):1024-1032.
[5]罗李平,俞元洪.具拟线性扩散系数的脉冲中立型抛物系统的(强)振动性[J].振动与冲击,2011,30(8):183-186.
[6]罗李平.具非线性扩散系数的脉冲时滞双曲型方程组的振动性[J].自然科学进展,2008,18(3):341-344.
[7]Luo L P,Liao J D,Gao Z H.Oscillation of systems of impulsive delay hyperbolic equations[J].International Journal of Applied Mathematics and Applications,2008,1(2):147-154.
[8]罗李平,欧阳自根.脉冲中立型时滞抛物偏微分方程组的振动准则[J].应用数学学报,2007,30(5):822-830.
[9]Luo L P.Oscillation theorem of systems of quasilinear impulsive delay hyperbolic equations[J].Northeast.Math.J.,2007,23(3):255-262.
[10]Yan J R,Kou C H.Oscillation of solutions of impulsive delay differential equations[J].J.Math.Anal.Appl.,2001,254 (2):358-370.
(Full)Oscillatory Criteria of Certain Impulsive Delay Parabolic Systems
LUO Li-ping
(College of Mathematics and Statistics,Hengyang Normal University,Hengyang Hunan 421002,China)
The(full)oscillation for a class of parabolic systems with impulsive perturbation and delay effect is investigated.By employing some results of first order impulsive delay differential inequalities,some sufficient criteria are obtained for the(full oscillation of all solutions of such systems under second boundary condition.The results fully indicate that the(full)oscillation is caused by impulses and delays.
(full)oscillation;parabolic system;impulse;delay
O175.26
A
1673-0313(2015)06-0023-04
2015-05-15
湖南省“十二五”重点建设学科项目(湘教发[2011]76号)
罗李平(1964-),男,湖南耒阳人,教授,主要从事(脉冲)偏微分系统解的性态研究。

