基于改进的灰色聚类关联分析的水质评价

阮艳荣，高茂庭，张颖

（上海海事大学信息工程学院，上海 201306）

基于改进的灰色聚类关联分析的水质评价

阮艳荣，高茂庭，张颖

（上海海事大学信息工程学院，上海 201306）

0　引言

为了全面、系统地分析评价水的质量，往往需要综合考虑对水质有影响的多种因素，因此，水质评价是一种多指标综合评价。目前，水质评价有很多种方法，主要有：分级加权平均法、综合污染指数法、集对分析法、层次分析法和灰色系统分析法等［1］。灰色系统理论自1982年邓聚龙教授创立以来得到了迅速的发展。灰色系统分析法通过白化函数的关联度使系统中的灰色性得以量化，在环境科学的研究中应用广泛并已显示出其优越性。

灰色聚类法和灰色关联分析法是灰色系统分析法中两种常用的方法，在环境质量评价中得到广泛使用［2］。灰色聚类法是建立在灰数的白化函数的基础上的一种多维灰色评估方法，但其在使用中也逐渐暴露出不足，主要表现在：白化函数往往采用降半梯形构造，忽略了不相邻等级之间的影响，权重采用了单阈值法，没有考虑各污染物在相同质量级别之间的变化幅度，导致评价结果出现偏差［3］。灰色关联法是通过灰色关联度来直接表示评价样本与各级别之间的几何贴近程度，是一种直接法，具有直观可靠、计算简单等特点，其弱点是关联度难以体现污染级别是一个范围（或区间），而不是某个确定值这个实际情况，从而有时会使评价结果出现较大偏差，另外，其评价值的分辨率也比较低［4-5］。

为此，将灰色聚类法和灰色关联分析法相结合取长补短，形成灰色聚类关联分析法，该方法的信息利用率及评价结果的分析率较高，除能对各测点进行准确的综合评价外，还能区分多测点环境质量的优势［6］。本文采用指数型白化函数、修正聚类权重计算，再与灰色关联法相结合，对灰色聚类关联分析法进行改进，并应用于水质评价中。

1　灰色聚类关联分析法

灰色聚类关联分析法先利用灰色聚类法计算水质样本对各个等级的从属度，然后再分别计算水质样本与清晰综合评判间的灰色关联度，再根据关联度的大小来确定各监测点水质的相对优劣［7-9］。灰色聚类关联分析法的步骤如图1所示。

在构建白化函数过程中，为使每一级别的白化函数与所有级别都存在隶属关系，避免零权重，综合考虑各个指标评价标准与实测值的关系，借鉴指数型白化函数思想，考虑水质类别划分规模对白化函数值的影响，并对白化函数进行相应调整，引用修正聚类权法不仅考虑了样本的实测值，而且涉及水质标准中各等级的标准值。

图1　灰色聚类关联分析法的步骤

同时，考虑到不同评价因子在同水质量级别之间标准值的变化幅度的不同，本文采用修正聚类权重计算，不仅考虑了样本的实测值，而且涉及水质量标准中各等级的标准值。算法中，把水质样本作为聚类对象，以样本的量化性质作为样本指标。

设有m个评价样本（各个年份水质监测数据平均值），每个样本有n个评价指标，若将水质状况分为p个类别，则有p个灰类，于是，每个评价指标也同样分为p个灰类 （聚类灰数），xij为第i个评价样本关于第j指标的实测值（聚类白化数），i=1，2，…，m；j=1，2，…，n；k=1，2，…，p。

1.1改进的白化函数

传统的白化函数采用“降半梯形”的形式，每一级别的白化函数仅与相邻上、下两个级别存在隶属关系，将不相邻等级的权重视为零时，无形中提高了相邻等级的权重，当污染级别浓度分布过于离散时，可能会遗失很多有用的信息，使评价结果出现误差，为了避免这一情况，本文引用了指数型白化函数，利用曲边代替“梯形结构”的直边。改进的白化函数构造原则为：（1）能够覆盖所有范围内的监测值；（2）整个范围内函数曲线是平滑的；（3）与区间距离相同的监测值其白化函数值也相同［10］。

本文的指数型白化函数如下［11］：

令yjk为评价指标j隶属于k等级的质量标准值，基于f1（x）与f2（x）的指数型白化函数分别表达为式（1）、式（2）和式（3）：

第j个评价指标第1个灰类的白化函数为：

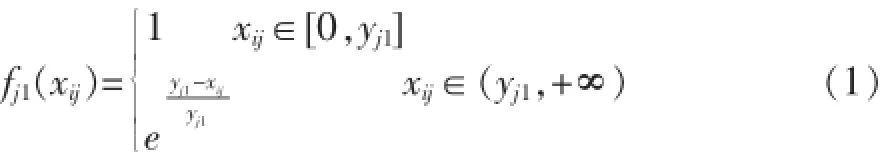
第j个指标第k（2≤k≤p-1）个灰类的白化函数为：

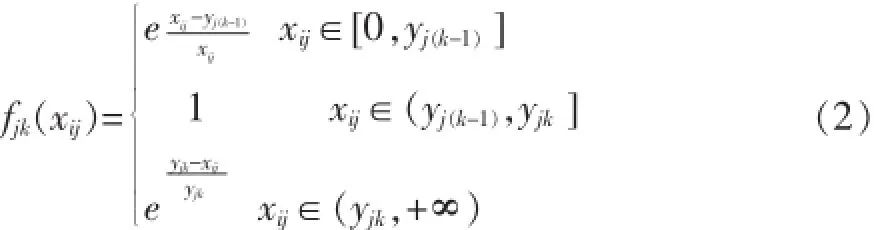
第j个指标第p个（最后一个）灰类的白化函数为

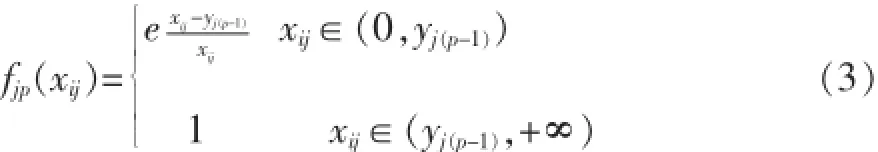
1.2改进的权重

灰色聚类权μjk是衡量各个指标对同一灰类的权重，表示指标j对第k个灰类的权重。计算聚类权重时需对标准值与样本值进行无量纲处理，计算公式如式（4）：

聚类权重计算公式为式（5）：

1.3灰色关联度的计算［12-14］

记评价样本i的第j指标关于第k类水质的白化函数为zik（j），可以通过式（1）-式（3）中fjk计算。

如果评价样本i的实测值对所有指标在水质类别k的白化函数值均为1，即zik（j）=1，那么该评价样本的水质为k类，所以若取z0k=（1，1，，1），则z0k是一个清晰的综合评判。

以 z0k作为参考数列，以 zik=（zik（1），zik（2），…，zik（n））作为被比较数列，计算其关联度rik（j）。

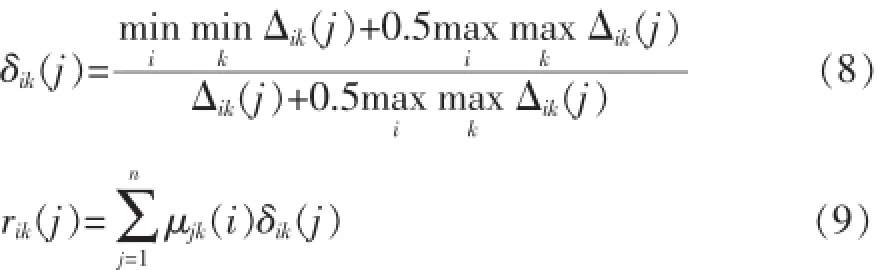
其中，Δik（j）=|zik（j）-z0k（j）|=|zik（j）-1|。

对于评价样本i，找出rik（评价样本i的水质关联度矩阵）中的最大值，该最大值对应的k值即为评价样本i的水质类别。?

2　应用实例

上海青浦急水港和浙江湖州新塘港是太湖流域的重点断面。太湖是我国第三大淡水湖，湖面有两千多平方公里，以太湖为中心的太湖流域，包括江苏南部、浙江北部、上海市和安徽省一小部分。随着城市经济的发展，水污染日益严重，采用改进的灰色聚类关联分析法进行评价，旨在了解急水港和新塘港的水质状况，识别主要污染物，为两地区的水质管理提供指导。

2.1实验数据

本文分别以上海青浦急水港和浙江湖州新塘港两个监测点2009-2013年的水质总体平均数据作为评价应用实例［15］，经初步分析发现其主要污染指标为：溶解氧（DO）、高锰酸盐指数（CODMn）、氨氮（NH3-N）、五日生化需氧量（BOD5）、氟化物（F-），故选用这5个指标作为评价因子，运用改进的灰色聚类关联分析法对水质进行综合评价，监测数据及评价标准见表1和表2。

2.2白化函数和聚类权值的计算

由于篇幅有限，白化函数和聚类权值的计算仅以急水港为例。

将表1的样本值和表2的标准值代入 （1）-（5）式分别求得白化函数和聚类权值，见表3，其中，斜线分开的分别为白化函数值与聚类权重。

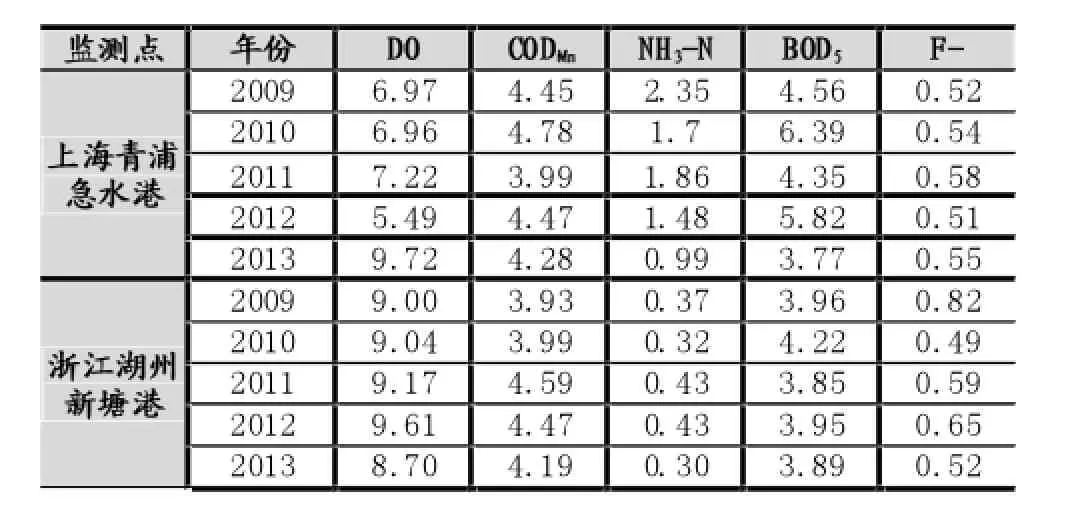
表1　上海青浦急水港、浙江湖州新塘港年平均质量浓度mg/l

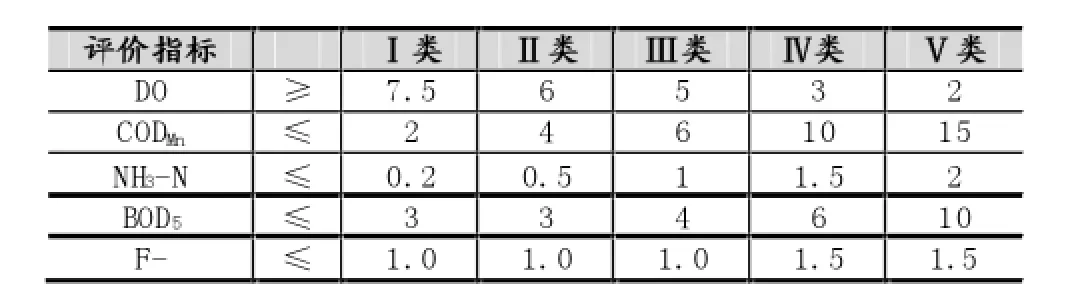
表2　地表水环境质量标准基本项目标准限值mg/l

2.3计算结果与比较分析

根据公式（6）-（9）计算得出各年份对水质类别的关联度，来判断各年份的水质级别，同理可得浙江湖州新塘港各年份对水质类别的关联度，与传统灰色聚类法相比较，结果见表4，其中，斜线分开的分别为急水港和新塘港两地的结果。

从表4评价结果可以看出，按传统灰色聚类分析法计算上海青浦区急水港和浙江湖州新塘港大部分年份的水质分别被评定为II级和Ⅲ级，而根据改进的灰色聚类关联分析法的计算，结果是上海青浦急水港水质为V级，而浙江湖州新塘港水质级别为II级。从各年监测数据上看，氨氮是主要污染物，上海青浦区急水港这些年份的氨氮值基本都超过II级标准值，浙江湖州新塘港的氨氮值都没超过II级标准值，因此该评价因子可以很大程度上影响综合评判结果，据此估测2009-2013年上海青浦急水港水质应更偏向于V级，浙江湖州新塘港的水质更偏向于II级，而传统灰色聚类法将其分别判定为II级，Ⅲ级，明显欠合理。另外，传统灰色聚类法的计算结果不同年份差异较大，而改进的灰色聚类关联分析法的计算结果不同年份差异较小。这说明在计算结果的稳定性上改进方法也优于传统方法。

3　结语

将改进的灰色聚类关联分析法应用于上海青浦急水港和浙江湖州新塘港的水质评价，得出急水港和浙江湖州新塘港2009-2013年的水质等级分别为V级和II级，说明上海急水港水污染比较严重，应加强水质管理。

通过指数型白化函数的计算反映实测值对水质标准各类别隶属度，建立了实测值与各灰类之间一一对应的关系，完全避免了零权重问题，提高了信息的利用程度；通过选用修正聚类权法确定各评价指标在不同级别中的权重，使得聚类评价结果更贴近实际；通过直接计算关联度来表示实测值与各水质类别的贴近程度，以准确判断该地区水质类别。改进的灰色聚类关联分析法易于掌握，计算简便，评价结果也更客观准确。

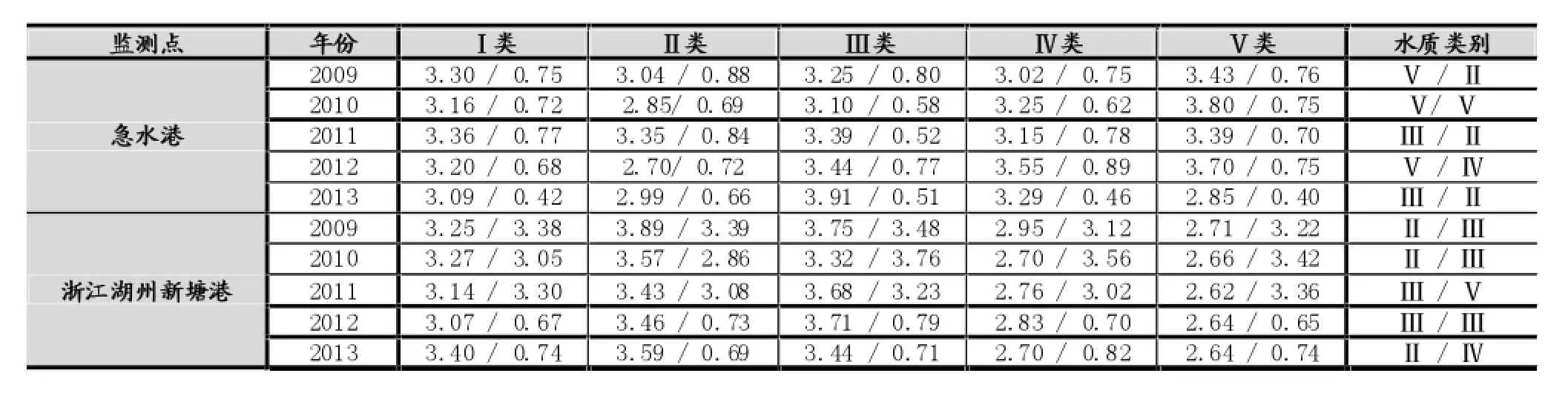
表4　急水港和新塘港各年份水质关联度计算结果与传统方法评价结果?

［1］张旭，汪长胜，郝庆菊.灰色聚类法在重庆北碚区境内支流河流水质评价中的应用［J］.中国农学通报，2010（2）：241-245.

［2］王清芬，王伯铎，马俊杰，王文春.用灰色聚类关联分析法对水环境质量的评价［J］.环境工程，2008（6）：59-64.

［3］胡军，许丽忠，张江山.基于改进灰色聚类法的大气环境质量综合评价［J］.福建师范大学学报（自然科学版），2012（1）：49-54.

［4］肖新平.灰色聚类关联分析法及其在大气环境质量评价中的应用［J］.环境科学进展，1997（8）：56-62.

［5］查金茂.环境质量综合评价的灰色聚类关联分析法［C］.武汉：武汉交通科技大学，1997：1082-1086.

［6］梁爱萍，侯祺棕，刘爱东.大气环境质量灰色聚类关联分析法的应用研究［J］.工业安全与环保，2005（6）：35-37.

［7］张云，邱艳，陈金发.灰色聚类关联评估在水环境质量评价中的应用［J］.节水灌溉，2010（2）：45-47.

［8］马艳琴，杨红艳，潘平奇.灰色聚类关联分析法的改进及应用［J］.数学的实践与认识，2013（6）：166-172.

［9］肖明，朱碧贵.用灰色聚类关联分析法对矿业城市大气环境灾害的评价［J］.兰州交通大学学报，2009（2）：121-124.

［10］朱碧贵，常青，闫彩云.基于改进灰色聚类关联分析法的城市大气环境质量评价［J］.兰州交通大学学报，2010（6）：135-138.

［11］徐卫国，张清宇，郭慧，何安标.灰色聚类模型的改进及应用研究［J］.数学的实践与认识，2016（6）：200-205.

［12］赵炎，王婷，徐曦.改进灰色聚类关联在地下水水质评价中的应用［J］.人民黄河，2012（7）：56-58.

［13］姚建玉，钟正燕，陈金发.灰色聚类关联评估在水环境质量评价中的应用［J］.环境科学与管理，2009（2）：172-174.

［14］马艳琴.改进的灰色聚类关联分析法在大气质量评价中的应用［J］.山东轻工业学院学报（自然科学版），2013（5）：63-66.

［15］H.Wong，B.Q.Hu.Application of interval clustering approach to water quality evaluation［J］.Journal of Hydrology，2013（5）：1-12.

Water Quality Evaluation；Gray Cluster Relation Analysis；Exponential Whiteness Ffunction；Modified Clustering Weight

Water Quality Evaluation Based on Improved Gray Clustering Relation

RUAN Yan-rong，GAO Mao-ting，ZHANG Ying
（College of Information Engineering，Shanghai Maritime University，Shanghai 201306）

国家自然科学基金项目（61273068）、上海市科委科技创新项目（12595810200）、上海海事大学科研项目

1007-1423（2015）20-0067-05

10.3969/j.issn.1007-1423.2015.20.015

阮艳荣（1989－），女，山东聊城人，硕士，研究方向为数据挖掘、水质监测系统

高茂庭（1963－），男，江西九江人，博士，教授，系统分析员，CCF高级会员，研究方向为智能信息处理、数据库与信息系统

张颖（1968-），男，副教授，从事领域为智能信息处理、多传感器信息融合、海洋环境监测、传感器网络等研究

2015-01-18

2015-07-04

采用指数型白化函数建立实测值与各等级之间的对应关系，避免零权重问题，通过修正聚类权重计算体现各评价因子在同一灰类之间的变化幅度，对灰色聚类关联法将进行改进，并应用于水质评价中。对上海青浦急水港和浙江湖州新塘港2009-2013年的水质进行综合评价，结果表明，改进后的灰色聚类关联分析法评价结果更为客观准确。

水质评价；灰色聚类关联分析法；指数型白化函数；修正聚类权

Exponential whiteness function establishes the correspondence between the measured values and each grade to avoid the problem of zero weight，and the modified clustering weight reflects the each evaluation factor's amplitude in the same grade of water quality.Applies the improved grey clustering relation analysis method in the water quality evaluation.After applied to water quality evaluation in Jishui Port Qingpu Shanghai and Xintang Port Huzhou Zhejiang from 2009 to 2013，the result shows that the improved grey clustering method can get evaluation result more objectively and accurately.