优化的初始中心点选取的K-means聚类算法

王金金，王未央

（上海海事大学信息工程学院，上海 201306）

优化的初始中心点选取的K-means聚类算法

王金金，王未央

（上海海事大学信息工程学院，上海 201306）

0　引言

数据挖掘中的一个重要研究方向就是聚类，它的思想是将数据集中的数据对象分为多个类或簇，在同一个簇或者类中的各个数据对象的相似程度尽可能做到最大，而不同簇或类之间的数据对象的相似程度尽可能的最小。为了将数据集群中的数据对象进行聚类，Han等人总结出了以划分、层次、密度、网络和模型为基础的五大类经典聚类算法。

K-means算法是一种简单、快速的基于划分的聚类算法，在实际应用中最为广泛，它能够在一些具有数值属性的数据的聚类中体现出聚类算法对几何和统计学上的重大影响。然而，传统的K-means算法具有凭借着具体的实际经验制定k值、对初始的聚类中心异常敏感、会随聚类中心的不同而得到不同的聚类结果等弊端，使得它很少会得到整个数据集的最佳聚类结果，并且随机的选定初始聚类中心导致其结果经常局限于局部的最优解，从而使得到的结果非常不精确。所以为了获得更好的聚类效果，找到一组较优的初始中心点和去除聚类结果的波动性对K-means算法具有重大的意义。

研究者们从聚类收敛条件、k值的选取、初始聚类中心的选择和处理分类属性数据四个方面进行改进。本文主要从初始聚类中心选择这一方面对该算法做出改进，使得算法的精确度和效率都有所提高。

1　K-means算法的基本思想

K-means均值算法的基本思想是：从数据集中任意选取k个数据作为k个聚类的初始中心点，数据集中其余的数据依据距离最小的原则，划分到离它最近的初始中心点这一组中，对于初始划分的每一组，计算出组中所有数据对该数组中心距离的平均值来当作新的聚类中心点，重复执行上述步骤，直到使得平方误差准则函数收敛为止。其中平方误差准则函数如（1）：

在公式（1）中，E是整个分组得到的样本空间中所有数据对象的到中心点的距离与平均距离的差的平方的和，xi是需要聚类的数据集中属于类Ci的数据样本，ai是类Ci中所有样本的平均值［3］。K-means算法的具体步骤如下：

（1）从包含n个数据的数据集U中任意挑选出k个样本数据作为k个类的初始中心，记为a1（0），a2（0），a3（0），…，ak（0）。

（2）将整个数据集U中的数据对象xi依次依据距离最小的原则分配给随机选取的k个类中的某一类Ci（t），i∈｛1，2，3，…，k｝，t代表迭代计算的次数，即如果Di（t）=min｛||x-aj（t）||，j=1，2，3，…，k｝，则x分类到类Ci（t+1）中，i∈｛1，2，3，…，k｝。

（3）计算出再分类的聚类中心，具体计算公式如下：

在公式（2）中，类Ci（t+1）中样本的数据个数是，新得的聚类中心就是类数据对象距离的平均值，从而使公式（1）达到最小。

2　初始聚类中心优化的K-means算法

2.1改进的算法思想

一般情况下，处于数据集的低密度区域的数据对象被称为孤立点或者噪声点［6］。为了避免噪声数据的干扰，我们首先要对这些噪声点或者孤立点进行删除；而对于其余的数据点，我们将数据对象之间的欧氏距离当作判定数据对象相似度的一个衡量准则，因此，我们就得计算出相邻数据对象之间的欧氏距离，然后我们将处于高密度区域中的数据对象来作为初始的聚类中心点。

我们选取的初始聚类中心点都位于整个数据集中的高密度区域范围内，它能很好地说明整个数据集中的数据分布情况，从而消除了传统的K-means算法依赖于聚类中心的缺陷，并提高K-means聚类结果的精度。

另外，在高密度区域中选择数据对象当作初始聚类中心点，我们必须计算出数据对象之间的距离。对于多维属性的数据对象，计算它们之间的距离，我们需要耗费大量的时间，尤其是那些高维属性的对象，距离的计算就必将耗费更多的时间。所以，在本文中提出了建立一个二维数组来存储数据对象之间的距离，对初始聚类中心选择的衡量标准中密度大小是一方面，另一方面，为下一个K-means聚类提供直接的距离值，从而减少时间并更能提高运行效率。

2.2相关参数的定义

（1）点密度：对于数据集U中的样本点x，以x为球心，以某一正数r为半径的球形区域中所包含的样本点的个数，称之为点密度，记作Dens（x）［3］。

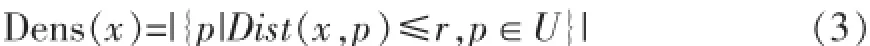
在公式（3）中，Dist（x，p）表示相邻数据对象的欧氏距离。

（2）孤立点（噪声点）：数据集U中的数据对象xi，计算xi到其相邻点的距离的平均值，计算公式如（4）：

把所有点按从小到大序列排序，当相邻两点之间的平均值大于某一阈值，则判断此点为孤立点并去除孤立点。

2.3算法的一般描述

输入：聚类数k和含有n个数据对象的数据集；

输出：达到目标函数值中最小的k个聚类结果。

具体的实现步骤如下：

（1）计算出相邻的两个数据对象的距离d（xi，yj）；

（2）按照公式（5）将每一个数据对象到其相邻数据对象的距离的平均值计算出来，并将判定为是孤立点的数据对象删掉，从而得到高密度区域的数据对象的集合D；

（3）将具有最大密度的数据样本当作第一个中心a1加入到集合A中，同时将其从D中删除；

（4）在数据对象集合D中找到离集合A最远的点，加入到集合A中，同时将其从集合D中删除；

（5）重复步骤（4），直到A中的数据对象的个数达到k个；

（6）按照选出来的k个聚类中心，运用 K-means聚类算法得到最终的聚类结果。

3　实验分析

3.1实验一

有一个专门用于测试数据挖掘算法和机器学习的UCI［4］数据库，在这个数据库中有专门为测试聚类算法性能而存在的的数据集，所以我们可以用精确度来直接表示聚类的质量。在实验中的实验数据集是UCI数据库中的常用的Iris数据集和Wine数据集，使用它们来证明优化的初始中心选取的K-means算法的效果，各数据集的概况在表1中体现：

表1　UCI数据集

在实验时，本文中分别用随机选择初始聚类中心的传统K-means聚类算法、文献中的改进算法以及本文提出的优化的初始聚类中心选择的聚类算法对上述两个数据集进行了5次聚类实验。通过对实验结果的分析和计算得到如下两个实验结果表格，具体如表2、表3所示：

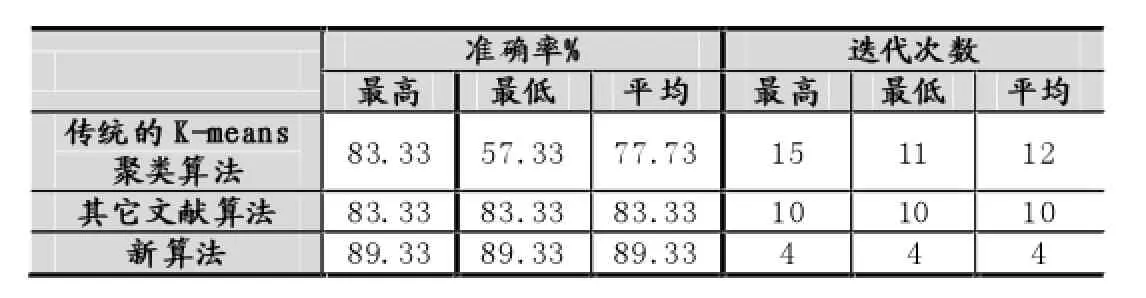
表2　三种算法对Iris数据集的测试结果表

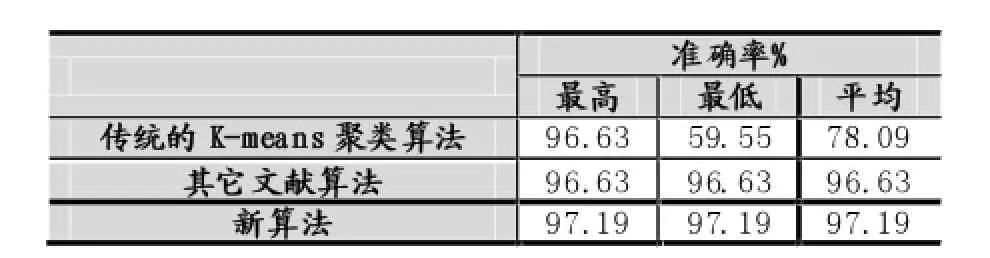
表3　三种算法对wine数据集的测试结果表

其他文献中的算法与传统的K-means聚类算法相比，使得对初始聚类中心的敏感性得到消除，算法相对比较稳定并且使得精确度有所提高，但是与文本提出的新算法相比较，本文提出的新算法不仅对初始聚类中心的依赖消除而且使得聚类结果的精确度更加准确，同时提高了聚类的运算效率。针对拥有250个数据Iris数据集分成四类，用传统的随机选取初始中心的K-means算法，实验5次，得到的最高准确率能够达到83.33%，最低准确率仅仅才57.33%，虽然其他文献中的算法精确度可以稳定在83.33%的较高水平上，但是本文提出的新算法在保证计算结果稳定的同时，达到了更高的精确度，为89.33%；再通过三种算法的迭代次数可以看出，本文提出的优化的初始中心点选取的K-means聚类算法相对于传统的K-means算法，以及其他文献中提出的算法大大地提高了运算的效率和聚

3.2实验二

下面这个实验是选取了UCI数据库中的含有150个数据对象的Iris数据集，其中每个数据对象有4个属性，我们通过实验是将数据集分成3类，根据Iris数据集中间的二维数据进行聚类，分别用传统K-means算法随机选取聚类中心的聚类算法和本文提出的优化的初始中心点选取的K-means聚类算法进行聚类。通过实验我们得到了如下的聚类结果图，在实验结果图中，圆圈、三角形、五角星分别代表一类数据。具体的实验结果如图1所示。

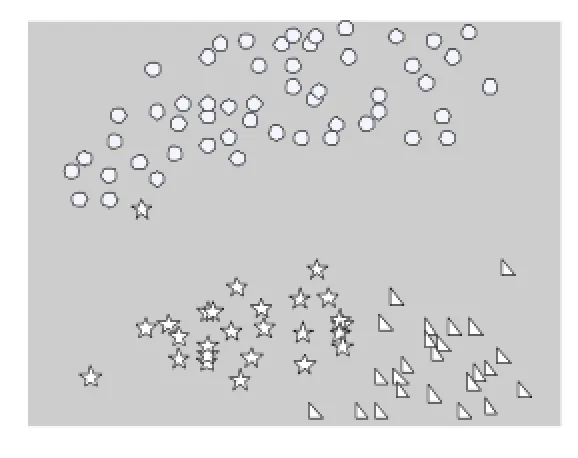
图1　传统K-means随机选取聚类中心的聚类算法

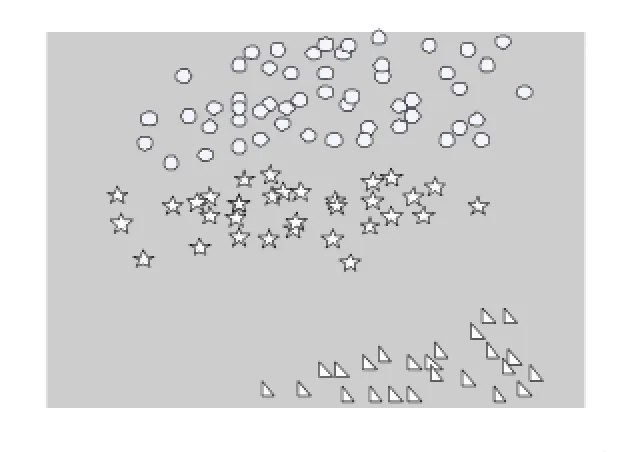
图2　优化的初始中心点选取的K-means聚类算法

从上述的两个实验的实验结果可以看出，本文中所提出的优化的初始中心点选取的K-means聚类算法，既可保证计算结果的稳定性，更进一步提高了算法的精确度。同时在计算过程中，本文算法的计算时间少于传统算法平均时间，迭代次数也远远小于传统算法，类的精确度。我们将含有278条数据的Wine数据集分成4类，经过5次传统K-means聚类算法的实验能够达到的最高准确率是96.07%，而最低准确率仅仅是59.55%，通过其他文献中提出的算法进行的实验，其准确率能够稳定的达到96.63%，但是还是没有超过本文提出的优化的初始中心点选取的K-means聚类算法所达到97.19%的准确率。很好地提高了算法的运算效率。

4　结语

随着互联网用户的增加和数据库的庞大发展，聚类人物所设计的数据量越来越庞大，传统的K-means聚类算法的应用相当广范，但其聚类效率和聚类结果会随着初始聚类中心以及数据量的改变而改变，严重影响了这种算法聚类的精确度；对于这个问题很多研究专家分别从各个不同的角度对K-means算法作出了改进。在本文中提出了一种优化的初始中心点选取的K-means聚类算法，并通过实验结果的对比得出，利用该算法能够更好地提高聚类的精确度，并且利用计算过程中通过数组来存储对象的方法，很大地提高了算法的运算效率。

［1］周爱武，于亚飞.K-means聚类算法的研究［J］.计算机技术与发展，2011.02：2.

［2］王赛芳，戴芳，王万斌，张晓宇.基于初始聚类中心优化的K-均值的算法［J］.计算机工程与科学，2010，32（10）.

［3］汪中，刘贵全，陈恩红.一种优化初始中心点的K-means算法［J］.模式识别与人工智能，2009，22（2）.

［4］韩凌波，王强，蒋正锋等.一种改进的K-means初始聚类中心选取算法［J］.计算机工程，2010，46（17）.

［5］孟子健，马江洪.一种可选初始聚类中心的改进K均值算法［J］.理论新探，2014，12（3）.

［6］顾洪博，张继怀.改进的k-均值算法在聚类分析中的应用［J］-西安科技大学学报2010，30（4）.

［7］曹志宇，张忠林，李元韬.快速查找初始聚类中心的K-means算法［J］.兰州交通大学学报，2009，28（6）：15-18.

［8］ESTER M，KRIEGEL H P，SANDER J，et al.A density-based algorithm for discovering clusters in large spatial databases with noise［J］. Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining.Portland：AAAI，1996：226-231.

［9］Gan W Y.Li D E.Hierarchical clustering based on kernel density estimation［J］-Journal of System Simulation，2004（02）.

Clustering；K-means Algorithm；Clustering；Outlier；Density

K-means Clustering Algorithm to Optimize the Initial Center Point

WANG Jin-jin，WANG Wei-yang
（Colleg of Information Engineering，Shanghai Maritime University，Shanghai 201306）

1007-1423（2015）20-0006-04

10.3969/j.issn.1007-1423.2015.20.002

王金金（1988-），女，山东潍坊人，在读硕士研究生，研究方向为港航物流管理

2015－05－13

2015－07－13

介绍一种可以对初始聚类中心进行优化的算法，改进之处是对孤立点进行特殊处理，降低孤立点敏感的问题，把距离与密度结合，选取最优的初始中心点，从而使聚类的精确度得到提高，并且该算法通过在计算的过程中存储数据对象之间的距离来提高算法的效率。通过对实验结果的分析，得到改进后的聚类算法可以有更好的精确度和更高的算法效率。

K-means算法；聚类中心；孤立点

王未央（1963-），女，江苏常熟人，副教授，研究方向为数据处理与挖掘

Describes an algorithm which initial cluster centers can be optimized.The improvement is to isolate point for special treatment，reduce outlier sensitive issue，combines the distance and density to select the appropriate initial focal point，so that improves the clustering accuracy，in order to improve the efficiency of the algorithm，the algorithm in the process of calculating the distance between the stored data objects.The experimental results prove that the improved clustering algorithm can achieve better results and higher efficiency of the algorithm.