从一题多解谈高阶行列式的计算方法
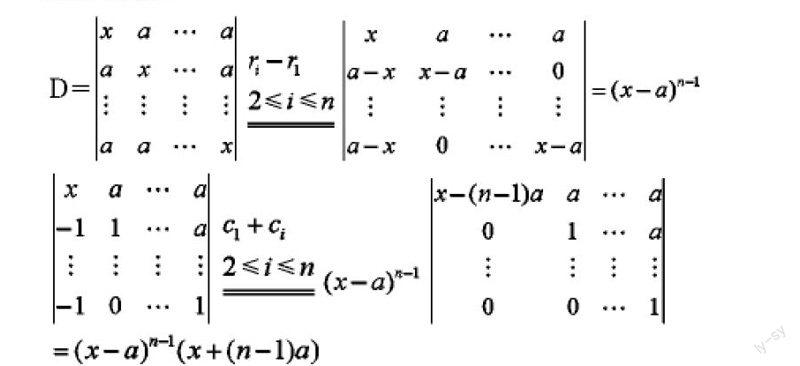
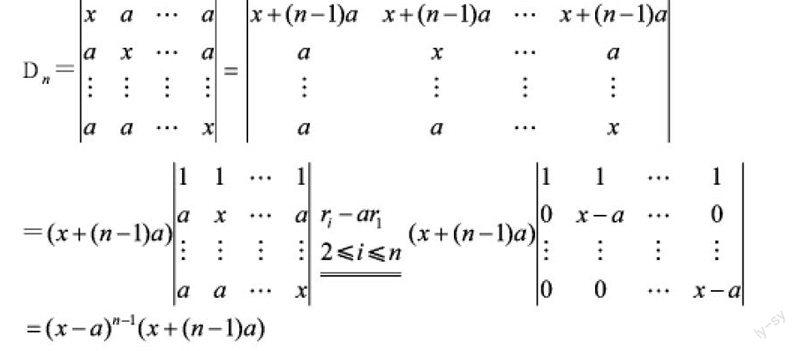
摘 要:行列式的计算是求解线性方程组的重要工具,是线性代数的基础。其中,高阶行列式的计算方法尤为重要。由于高阶行列式的计算应用定义法较为复杂,本文通过求解一道习题,给出计算高阶行列式除基本算法—— 化三角形法外,还有叠加法、加边法、析因法、辅助行列式、递推公式法和数学归纳法等6种计算方法,并给出每个方法适应的条件和解题步骤。行列式计算方法多种多样,高阶行列式形式虽然复杂,只要在计算过程中,仔细观察行列式的特点,选择恰当的计算方法,既可以在保证计算速度,又可以保证计算质量,还可以使高阶行列式的计算变得简单。计算就会变得比较容易。
关键词:高阶行列式 计算 方法
中图分类号:G71 文献标识码:A 文章编号:1674-098X(2015)07(b)-0224-02
行列式的计算是学习线性代数的基础,是求解线性方程组的基础,但行列式的计算方法很多,综合性较强。首先介绍一下行列式的定义与性质。
1 行列式的定义与性质
1.1 行列式的定义
将个数排成n行n列并在左右两边各加一竖线后得到的算式称为n阶行列式,通常用大写字母表示。记为。其中D为n阶行列式指的n!项的代数和,这些项是一切可能的取自D1的不同的行与不同的列上的n个元素的乘积。项的符号为,如果是偶排列时,这一项是正的,如果是奇排列时,这一项是负的。
1.2 行列式的性质
(1)性质1:行与列互换,行列式的值不变。
(2)性质2:交换两行(列)的位置,行列式的值变号。
(3)性质3:某行(列)的公因子可以提到行列式的符号外。
(4)性质4:如果某行(列)的所有元素都可以写成两项的和,则该行列式可以写成两个行列式的和;这两个行列式的这一行(列)的元素分别为对应的两数之一,其余各行(列)元素与原行列式相同。
(5)性质5:某行(列)的倍数加到另一行(列),行列式的值不变。
有以上性质还可以得出以下方面。
(1)推论1:两行(列)对应元素对应成比例,行列式的值为0。
(2)推论2:某行(列)元素全为0,行列式的值为0。
(3)推论3:两行(列)对应元素相同,行列式的值为0。
2 高阶行列式的计算方法与应用举例
行列式是求解线性方程组的重要工具,在很多领域都有重要的应用。在文献[7]中主要研究的是求解特殊行列式—— 缺行范德蒙行列式的计算方法,但是对应一般的高阶行列式没有归纳总结。
行列式的计算方法多种多样,一般用行列式的定义、性质、化三角形法等方法计算行列式,但对于一些高阶行列式或含有字母的行列式,用一般方法计算显得有些费劲,甚至是不容易求解出来。通过参考教材[1-3]及文献[4-6],收集一些计算行列式的计算方法。下面以一道题目为例,介绍几种计算高阶行列式的方法。
例Dn=
2.1 化三角形法
通过运用行列式的性质,对行(或列)进行消去变换,消去变换可将原行列式主对角线一侧的元素全化为零(三角行列式)。此方法是求解行列式最常用的方法。
例题解法1
2.2 叠加法
仔细观察这个行列式,会发现每一行(列)构成的元素相同,将第2行、第3行、…、第n行加到第一行再进行计算。该方法适用于每行(列)构成元素相同,即把所有的行(列)加起来相同。
例题解法2
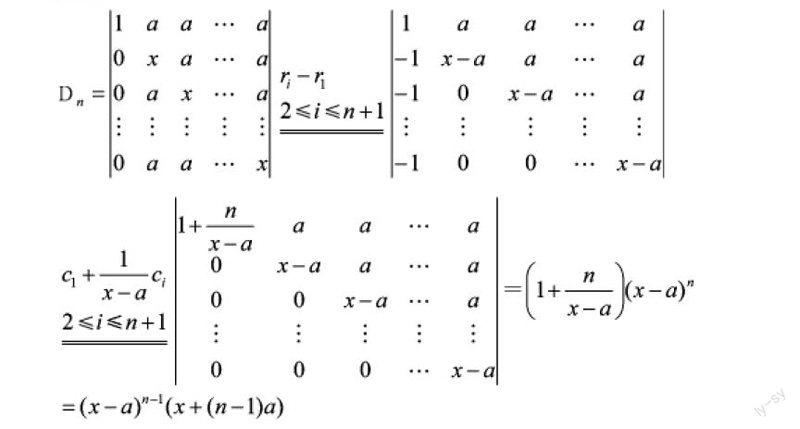
2.3 加边法
根据行列式的特点,在原行列式的基础上添行列使其升阶构造一个容易计算的新行列式,进而求出原行列式的值。此方法适合行列式除了字母以外行对应元素数字构成相同。
例题解法3
2.4 析因法
析因法是根据行列的性质结合多项式的理论而成的方法。如例题,可以将行列式Dn看作一个关于x的多项式f(x),然后对行列式施行某些变换或求导数,求出f(x)的互素的一次因式,使f(x)与这些因式的乘积h(x)只相差一个常数k,根据多项式相等的定义,比较f(x)与h(x)的某一项的系数,求出c值,便可求得Dn=ch(x)。
例题解法4
设Dn=f(x),根据Dn的形式,当x=a(行列式元素相同根据性质行列式值为0),x=(n-1)a(行列式的第一列是第2列、第3列、第4列…、第n列的和,根据行列式的性质可知行列式值为0)是Dn=0,所以(x-a)、(x-(n-1)a)是f(x)的一次因子。
根据行列式的求导法则,可以得:
一般地,递推公式法是根据行列式的性质,然后按行(列)展开,把一个n阶行列式表示为具有相同结构的较低阶行列式的线性关系,再把再根据此关系递推求得所给行列式的值。
2.6 数学归纳法
数学归纳法是常用的证明方法,利用数学归纳法来计算行列式分两步进行:第一步是发现和猜想;第二步是证明猜想的正确性。
一般地,若要证的结果已知时,可用数学归纳法来证明,其步骤如下:(1)验证n取第一个值(n=0,1或2等)时公式成立;(2)假定n=k时公式成立,验证当n=k+1时公式也成立,若要求的结果未知时,也可先猜想其结果,然后用数学归纳法证明其猜想结果成立。
2.7 辅助行列式法[4]
辅助行列式法的解题步骤是:在行列式的各元素中加上一个数x,使新行列式除主对角线外,其余各元素均为0,然后计算新行列式的主对角线上各元素的代数余子式,最后所求行列式。
例题解法7
对行列式每一个元素加-a,得到的新行列式为:
通过上述计算,可以看出行列式的计算是灵活多样的,只要在高阶行列式的计算过程中,仔细观察行列式的特点,选择恰当的计算方法,既可以在保证计算速度,又可以保证计算质量,还可以使高阶行列式的计算变得简单。该文通过例题的多解,总结求解计算高阶行列式的几种方法。
参考文献
[1]张禾瑞,郝炳新.高等代数(第4版)[M].北京:高等教育出版社,1997.
[2]北京大学数学系几何与代数教研室代数小组编.高等代数(第2版)[M].北京:高等教育出版社,2003.
[3]徐仲,陆全,张凯院,等.高等代数(北大·第3版)导教·导学·导考[M].西安:西北工业大学出版社,2003.
[4]卢潮辉.从一题多解谈行列式的计算[J].牡丹江教育学院学报,2010,119(1):144-145.
[5]张瑜,张越.浅谈递推法在行列式计算中的应用[J].赤峰学院学报:自然科学版,2014,30(17):5-7.
[6]张蕾.行列式的计算[J].科技资讯,2014(29):125-127.
[7]于荣娟,陈红红,杨海波.浅谈某类行列式的计算[J].内蒙古农业大学学报:自然科学版,2013,34(2):161-164.

