减小光栅传感器测量信号误差的研究
李华丰 李强 万宇


摘 要:光栅传感器是一种新型光子器件,将其应用于军事、航空等领域的检测工作中,可获得比传统机电机械类传感器更稳定、更可靠以及更准确的测量信号。但是,由于系统自身误差及噪音的影响,使得当前光栅传感器测量精度依旧有上升的空间。当前,光栅传感器作为一种新型传感器,凭借着高灵敏度、高分辨率等等优势,得到了十分广泛的应用。但是,在光栅传感器应用过程中,也存在一定的测量信号系统误差和随机误差,本研究即针对如何减小光栅传感器测量信号误差这一问题,展开了具体的探讨。
关键词:光栅传感器 测量信号 误差 工作原理
中图分类号:TH822 文献标识码:A 文章编号:1674-098X(2015)07(b)-0013-02
1 光栅传感器测量工作原理及其信号误差概述
1.1 光栅传感器测量工作原理
在光学领域中,反射镜与光学衍射光栅均是常用的设备。其中,光学衍射光栅即为在一个不透明的平面上刻出N条平行且具有一定间距的狭缝,通过其实现入射平面波振幅的有效调制。对于光栅传感器而言,其主要是利用相位的调制获得衍射光栅,具体来说就是在光传播经由的路径中摆设一块透明的物体,此时透射波相位是由光在该透明物体中的光程所决定,基于此可通过改变透明物体厚度,实现光程的变化,达到调制透射波相位的目的[1]。
如式(1)所示,即为纤芯折射率调制周期:
(1)
式中:—固定紫外光源波长;
—两相干光束所构成的夹角。
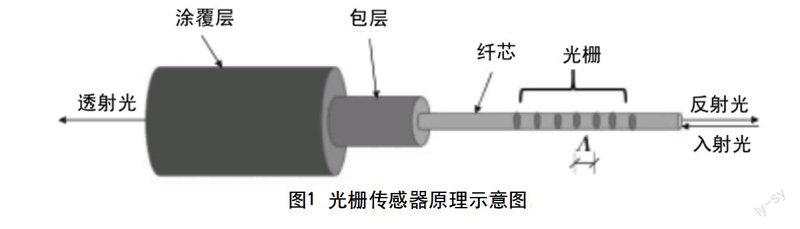
光栅在进行宽带光波的调制时,受到的限制较大,仅仅能够在较小的频率范围进行调整。图1即为光栅传感器原理示意图,宽带光波射入光栅传感器后,其仅能在一定的窄频范围内进行相应的反射或是透射,已达到筛选的目的。如式(2)所示,即为反射中心波长的计算公式:
(2)
式中:—反射光中心波长;
—有效折射率;
—光栅周期。
对此,可通过不同的波长,获得测量对象的相关参数。
1.2 光栅传感器测量信号误差类型
在光栅传感器的实际应用中,其测量信号的误差主要可以分为两种:一是系统误差,主要有细分误差、周期累计误差;二是随机误差。对于光栅传感器测量系统而言,一旦出现信号误差,即会影响到测量结果的准确性,因此必须重视光栅传感器测量信号误差的查找和修正。一方面,针对光栅传感器测量信号系统误差,可采取相应的误差修正技术;另一方面,针对光栅传感器测量信号随机误差,可通过多项式预测滤波器的应用实现误差的有效减小。
2 减小光栅传感器测量信号系统误差的措施
2.1 误差检测
在光栅测量系统的应用中,利用精密导轨将激光干涉仪与其相连接,注意必须确保其测量轴线处于同一直线,从而达到阿贝原则的要求。在进行光栅测量的过程中,应通过同步动态检测,实现光栅测量系统与激光干涉仪测量数据的同时刻采样,并将其传送至计算机处进行相应的分析处理[2]。
2.2 误差分离
在光栅传感器实际测量工作中,可采取傅里叶变换或是离散频谱分析的方法,将检测出来的系统误差中的细分误差与周期累计误差进行分离处理。其中,细分误差即为总检测结果中基频和莫尔条纹空间频率基本相同的部分;周期累计误差,则可利用低通滤波方法,将剩余部分中的随机误差滤去后得到。
2.3 误差补偿
为了实现光栅传感器测量信号系统误差的有效减小,必须采取相应的误差补偿措施,其主要包括以下三种:(1)归一补偿。该种补偿措施应用过程中,补偿数值与当前所处的测量位置不存在直接的联席,因此十分适合在无绝对零位的光栅测量系统中使用。但是若测量系统的误差较大,则会因为补偿精度不够,产生补偿不彻底的问题。(2)分段补偿。在实际应用中,只要分段数达到一定的规模,则可获得较为精确的补偿值。但是,由于该种补偿措施会产生大量的表格数据,因此对于存储空间的要求较高,也极易导致整体测量速度减慢。(3)混合补偿。该种补偿方法可以说是兼顾测量速度与精度,应用范围较为广泛。
2.3.1 归一补偿方法
该种补偿方式即为在全量程的所有位置,通过相同的补偿参数进行误差的修正。一方面,针对周期累计误差,利用同一条直线进行线性补偿;另一方面,针对细分误差,则利用的是同一条细分误差补偿曲线。如式(3)即为归一补偿之后的位移计算:
式中:—斜率补偿系数;
—周期累计误差固定偏移量;
—细分误差曲线。
在式(3)中,因为是个固定的值,假设给定一个值为0,并不会影响到最终的结果,故可得到式(4):
2.3.2 分段补偿方法
该种补偿方式即为把全量程换分为N段,各段之间的补偿参数并不相同,而是由各自的误差特性做决定,如式(5)所示即为分段补偿之后的位移计算:
式中:—第k段细分误差函数;
—第k段周期累计误差补偿系数;
—第k段的周期累计误差的偏移值。
3 减小光栅传感器测量信号随机误差的措施
在光栅传感器测量的实际应用中,为了最大程度地减小其测量信号的随机误差,则必须实现传感器所输出的莫尔条纹信号的细分。值得注意的是,信号细分的精度会直接受到高斯白噪声与脉冲型噪声的直接影响。对此,减小光栅传感器测量信号随机误差的直接办法就是减小噪声干扰。根据实践可以发现,通过中值与平均滤波的方法,可以在一定程度上降低噪声的影响,但其更宜用于静态测量,由于莫尔条纹信号经常变化,这也就导致其应用效果大打折扣[3]。据此,本研究提出利用多项式预测滤波器,减小光栅测量信号中的噪声。
3.1 多项式预测滤波器
如式(6)所示,即为使用一个L阶多项式表示了传感器的输出信号:
式中:—多项式系数;
—测量信号随机误差。
如式(7)所示,即为利用多项式预测滤波器,对当前测量信号的预测:
式中:—的预测值;
—阶多项式预测滤波器系数。
在排除噪声的基础上,通过滤波器的信号不变,即,具体如式(8)所示:
将式(8)中的右边展开,可得出个约束条件公式:
设每个采样值噪声成分相互独立,则可得到滤波器的噪声增益如式(11)所示:
如上所示,式(11)属于性能泛函,在进行滤波器系数的设计师,应采用式(9)、式(10)作为约束条件,使得式(11)取极小值。式(12)即为通过拉格朗日乘子法得到的增广泛函:
(12)
式中:、是乘子。先对式(12)中的、、求偏导数,要求等式为零。
现令,分别对式(13)、式(14)、式(15)进行求解:
值得注意的是,若是令,则多项式预测滤波器就直接成为了一个平均滤波器。
3.2 传感器信号滤波处理
由于光栅传感器测量输出信号处于一个动态的变化过程中,这就使得若是仅仅将某一阶的多项式进行相应的预测滤波处理,就会导致很大的误差。此外,由于在信号中还存在脉冲噪声,若是采用中值滤波的方法,则会导致输出滞后,不利于测量误差的减小。对此,在进行传感器信号滤波处理时,应使用零阶、一阶、二阶预测信号与测量信号组合的中值滤波,从而实现以下几个目标:(1)信号水平区间,平均滤波器发挥着主要的作用;(2)信号斜坡区间,一阶预测滤波器发挥着主要的作用;(3)信号曲线区间,二阶预测滤波器发挥着主要的作用;(4)通过中值滤波实现脉冲噪声的降低。如式(18)所示即为中值滤波器输出:
(18)
式中:—中值滤波器的输出;
—平均滤波器、一阶预测滤波器、二阶预测滤波器的输出信号值;
—n时传感器采样信号值。
3.3 实际应用
下文利用一个自制光栅,采取相应措施减小光栅传感器测量信号随机误差。该光栅长度是10cm,栅距是1mm,现采取多点插值算法进行莫尔条纹信号的细分处理。但是,因为噪声因素的干扰,导致莫尔条纹信号的细分精度受到极大的影响,对此采取上文中的滤波算法减小光栅传感器测量信号误差,提高精度。现将Heidenhaing高精度光栅作为基准纹尺(其分辨力是0.1μm,准确度是±0.2μm),在一栅距中一共测试16个点,具体数据见表1。通过表1中的数据可以看出,采用了上述滤波方法后,光栅分辨力达1μm。
4 结语
综上所述,光栅测量信号中的误差可分为系统和随机两种,一方面,针对系统误差应采用相应的误差修正技术,实现误差的合理检测、分离、补偿;另一方面,针对随机误差应采用多项式预测滤波和中值滤波相结合的方法,实现噪声干扰的有效减小。
参考文献
[1]吴付岗,姜德生,何伟.基于相关分析的光纤光栅Bragg波长偏移值测量[J].计算机测量与控制,2007,15(5):593-594.
[2]胡晓东,彭琅.一种新的光栅传感器信号相位补偿算法的设计[J].自动化与仪表,2011,26(9):11-14.
[3]高贯斌,王文,林铿,等.圆光栅角度传感器的误差补偿及参数辨识[J].光学精密工程,2010,18(8):1766-1772.

