不同的内容 同样的精彩

张林

摘 要：教学内容的多样性和教学对象的差异性决定了教师不能采用一种方法和形式组织课堂教学，应以内容为主导，选择方法，找到切入点，采用不同的方法和策略，演绎出课堂的精彩。

关键词：圆柱的体积 教学灵感 人机氛围

【中图分类号】G 【文献标识码】B 【文章编号】1008-1216（2015）09B-0019-01

笔者在教学《圆柱的体积》一课，引导学生将圆柱转化成长方体、推导圆柱的体积公式时，学生们居然在小组合作探究的基础上得出了下面3种推导方法：

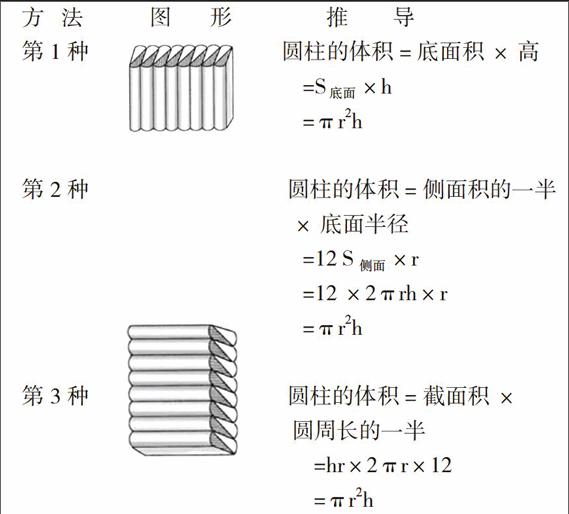
方   法            图       形                 推        导

第1种                                   圆柱的体积=底面积×高

=S底面×h

=πr2h

第2种                                    圆柱的体积=侧面积的一半

×底面半径

=12 S 侧面×r

=12 ×2πrh×r

=πr2h

第3种                                    圆柱的体积=截面积×

圆周长的一半

=hr×2πr×12

=πr2h

当时，有一种意外的惊喜，惊喜缘于后两种推导方法的巧妙。细细揣摩，可以从中发现3种推导方法的本质是一样的，都以长方体的体积公式作为基础，但其中体现出的思维过程不一样，正好体现了长方体摆放位置的3种变式，尤其是后两种推导方法体现了学生思维的创造性，真可谓“异曲同工”。学生们怎么能想到通过变换长方体摆放位置而得出圆柱体积的3种推导方法？笔者不禁想起了以前教学《长方体和正方体的体积》一课时，学生们在推导长方体的体积公式时也出现了类似的3种方法：

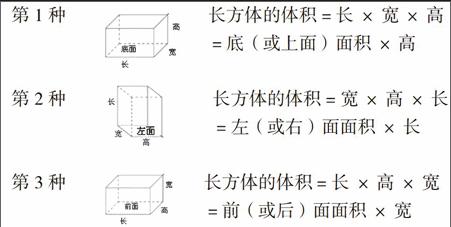
方     法：图形推导

第1种                                长方体的体积=长×宽×高

=底（或上面）面积×高

第2种                                 长方体的体积=宽×高×长

=左（或右）面面积×长

第3种                               长方体的体积=长×高×宽

=前（或后）面面积×宽

在学生得出第1种推导方法后，笔者发现一个学生正在摆弄手中的长方体，几种摆弄姿势正好体现了长方体摆放位置的3种变式。于是，笔者灵感顿生：“长方体的体积=底面积×高”这个公式中的“底面积”仅仅相当于“长×宽”吗？如果像后两种推导方法中那样摆放长方体，长方体的左（或）右面、前（或后）面不就成了“底面”吗？此时，长方体原先的“长”“宽”不就成了现在长方体的“高”吗？相对论告诉我们，物体的位置是相对的，不是绝对的。这样一来，长方体原先的体积公式不就可以转化成后两种形式吗？于是在笔者的引导之下，演绎出了后面的精彩。

思考：

1.教师的教学灵感是课堂精彩之花得以绽放的源头活水。试想，在“长方体的体积”教学中，当时如果缺乏教学灵感，能引导学生从不同的角度思考从而演绎出课堂的精彩吗？可见，教学灵感的捕捉很重要。教师的教学灵感有两个来源：一是内部诱因，即教师的教学创新动机;二是外部诱因，如学生的一种错误解法、一个异样举动等。在“长方体的体积”教学中，学生摆弄长方体的几种姿势就成了教师教学灵感发生的重要外部因素。教师教学灵感的发生，乃是教师教学智慧的体现。一个教师要想获得教学灵感，就必须在长期的教学中不断加强教学理论的学习，不断地进行教学实践思考，不断地丰富教学经验，这样才能使自己获得足够的教学智慧，从而使自己能够灵活应对和处理课堂上的各种突发事件，使课堂精彩灵动。

2.和谐的人际关系是课堂精彩之花得以绽放的适宜土壤。试想，在“长方体的体积”教学中，要是笔者对那位玩弄长方体的学生横眉冷对甚至大声呵斥，就会造成课堂气氛的沉闷紧张，学生能有后来的创新想法吗？正是由于笔者当时的冷静思考，善待了学生的缺点，创设了和谐的人际关系，捕捉住了稍纵即逝的教学灵感，加之自己的巧妙引导，才有了后来学生标新立异的想法。正是由于师生之间建立了和谐的人际关系，教学双方共同进入到了那微妙的心理相容的教学意境，彼此间产生了心灵的共鸣，才使课堂演绎出精彩，充盈着活力。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[2]曹培英.小学数学操作活动的教学模式[M].北京：人民教育出版社，2004 .

[3]吴亚萍，王芳.备课的改革[M].北京：教育科学出版社，2007.

[4]曹培英.小学数学操作活动的教学模式[M].北京：人民教育出版社，2004 .