某切边不规则凯威特单层球壳结构非线性屈曲分析

贺盛，陈庆军, 2, 3，姜正荣, 2，赖洪涛，刘红亮



某切边不规则凯威特单层球壳结构非线性屈曲分析

贺盛1，陈庆军1, 2, 3，姜正荣1, 2，赖洪涛4，刘红亮1

(1. 华南理工大学 土木与交通学院，广东 广州 510641；2. 华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510641；3. Centre for Infrastructure Engineering and Safety, The University of New South Wales,UNSW Sydney, 2052, Australia；4. 华南理工大学 建筑设计研究院，广东 广州 510641)

以某切边不规则凯威特单层球形网壳作为研究对象，研究由于开洞而造成的不规则、支承拱梁水平刚度和竖向刚度的变化、活载的非对称分布、初始几何缺陷、几何非线性以及材料弹塑性对网壳非线性屈曲性能的影响，并采用有限元软件 ANSYS对此结构进行非线性的荷载−位移全过程分析。研究结果表明：与完整球壳相比，切边球壳的稳定性能大幅度下降；与水平刚度相比，拱梁的竖向刚度对稳定性的影响较大；按一致缺陷模态法得到的稳定承载力系数，往往不是最小；初始几何缺陷值取跨度的1/400 较适宜；材料非线性对切边球壳稳定性的影响较大；活载的非对称分布对本结构的稳定性并无不利影响。

不规则切边；凯威特球形网壳；门洞；非线性屈曲；初始几何缺陷

网壳结构以其跨越能力大、刚度大、用料省、造型美观等特点，深受广大建筑师与结构师的青睐。其中，单层网壳则以构造简单、经济效益高等优点更胜一筹。但不可置否，当单层网壳的跨度较大时，其稳定性差的特点就尤为突出。由此可知，稳定性分析是单层网壳设计中关键的问题。自20世纪50年代以来，网壳稳定性问题在国际学术界中引起极大关注。无论是在弹性屈曲分析还是非线性屈曲分析上，均取得丰硕的成果[1−4]。而自20世纪80年代末开始，国内也兴起研究网壳稳定性的热潮。罗永峰等[5]提出：网壳结构的稳定分析只有在同时考虑几何大位移及弹塑性条件下，才能得到接近实际的结构承载能力。沈世钊[6]通过所完成的2 800余例各式网壳的全过程分析，揭示了不同类型网壳结构稳定性能的基本特性，并提出了单层球面网壳、柱面网壳和椭圆抛物面网壳稳定性承载力的实用计算公式。曹正罡等[7]研究了单层球面网壳在静力荷载作用下的弹塑性稳定性能。范峰等[8]研究了杆件失稳对网壳稳定性的影响。以上研究均针对完整网壳，对于不规则的网壳结构[9−10]研究较少。将完整的壳体进行切割，其壳面将被削弱，原有的力传递路线必然改变，进而对结构稳定性造成不利影响。球壳的切边、拱梁的水平与竖向刚度、网壳杆件截面刚度、活载的非对称分布、初始几何缺陷的模态和大小、几何非线性以及材料弹塑性等因素对此类网壳稳定性能的影响值得深入研究。在此，本文作者利用大型通用有限元软件ANSYS，以某实际工程中的切边不规则单层凯威特球形网壳作为分析对象，研究以上各因素对此类网壳稳定性的影响，并为此类网壳的设计提出参考。

1 工程概况

本工程位于广州某处，共有3个球壳结构，球体直径分别为22，32和36 m，其用途是作为观光旅游服务区及展厅等。本文以直径为36 m球壳结构作为研究对象。

本工程抗震设防烈度为6度。场地重现期50 a的基本风压为0.50 kN/m2，地面粗糙度为C类。地基土层主要为填土层、耕植土层、冲积土层、残积土层及燕山期花岗岩基岩5部分，场地土类型属于中软场地土，各地层均为不液化或不考虑液化地层，建筑场地类别为II类。

一般的单层球壳结构多为完整球壳，而由底层设置立柱形成入口门洞。但本工程由于建筑效果需要，入口处开6.5 m高拱形缺口和4.5 m高矩形缺口各1个，且四周支座直接落地。网壳展开图及杆件截面分布见图1。

图1 网壳展开图及杆件截面分布图

2 分析模型

采用通用有限元软件ANSYS进行整体建模，该空间结构均视为杆系结构，由于所有构件都采用刚性连接，因而都采用空间梁单元建模，拱梁及网壳杆件均采用BEAM188。钢材弹性模量取为2.06×105MPa，泊松比为0.3，密度为7 850 kg/m3，塑性本构采用两段式，屈服准则采用Von Mises准则，屈服强度为345 MPa。底部每个支座均采用了固接约束，限制了，和向平移自由度以及，和向的旋转自由度。结构模型如图2所示。

图2 结构模型图

相关的荷载取值包括：1) 屋面恒载，上部构件及连接件折算成面荷载为1.5 kN/m2，其中，玻璃罩的荷载为1.0 kN/m2，屋面吊挂荷载为0.5 kN/m2。钢结构质量由程序自动生成，并乘以1.1倍，考虑节点自重；2) 屋面活载，按照不上人屋面取0.5 kN/m2。

荷载组合包括组合Ⅰ(全跨恒载+全跨活载)和组合Ⅱ(全跨恒载+布置在球壳被削弱的半跨活载)。

根据球壳开洞与否、支承拱梁截面尺寸以及网壳杆件截面变化情况，建立12个不同的网壳模型，以考察以上因素对网壳稳定性能的影响。

将无门洞完整网壳结构命名为模型S0，其结构根据本凯威特工程的1/6完整模型复制生成；本工程模型定义为模型S1；模型S2~S5是在模型S1的基础上，逐渐增加大门拱梁高；模型S6~S8是在模型S1的基础上，逐渐增加大门拱梁宽；模型S9是在模型S1的基础上，减小网壳杆件截面；模型S10是在模型S1的基础上，增大网壳杆件截面。以上各模型均考虑荷载组合Ⅰ作用下的情况。S11的截面与S1的截面完全相同，但其考虑荷载组合Ⅱ作用下的情况。所有模型的小门拱梁截面总高×翼缘宽×腹板厚度×翼缘厚度为400 mm×800 mm×72 mm×12 mm。分析模型参数见表1。

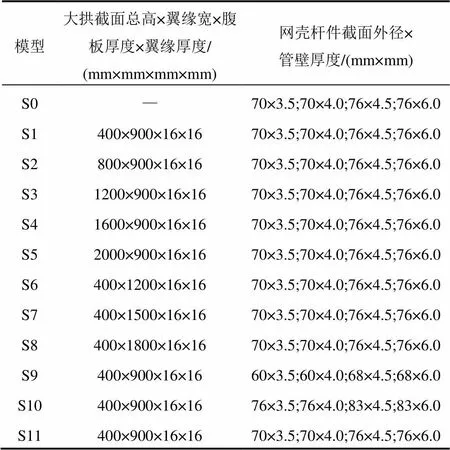
表1 分析模型参数

3 特征值屈曲分析

屈曲分析的特征值方程为

(L+G)=0 (1)

式中：为特征值；为特征位移向量；L为网壳的弹性刚度矩阵；G为初应力矩阵。式(1)的特征值方程为

|L+G| =0 (2)

特征值屈曲分析无需进行复杂的非线性分析便可得到理想弹性结构的临界荷载和屈曲形状，对预测屈曲荷载的上限及网壳的设计分析具有重要意义。本文采用Block-Lanczos方法，依次分析各模型的前20阶屈曲模态及对应的特征值。表2所示为各模型前8阶的弹性屈曲特征值，图3所示为模型S0，S1与S11的前3阶屈曲模态的对比图。

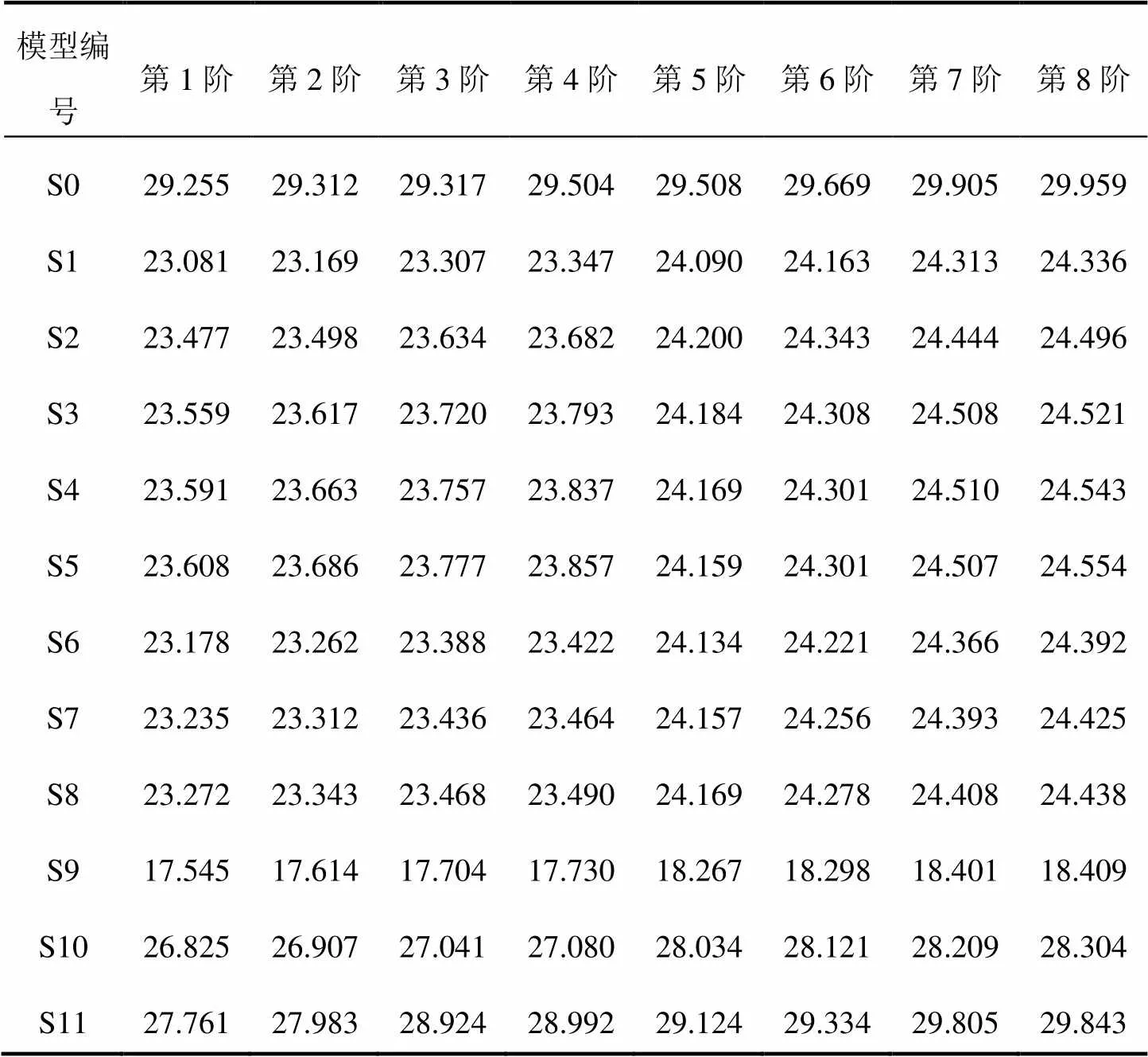
表2 屈曲特征值计算结果

(a) 第1阶；(b) 第2阶；(c) 第3阶

图3 S0，S1与S11的前三阶屈曲模态对比

Fig. 3 Comparison of the first 3 steps buckling mode among S0, S1 and S11

分析结果表明：门洞的设置对结构的特征值屈曲模态以及屈曲特征值均有一定影响。由图3可知：完整球壳S0的屈曲形状为整体屈曲；而切边球壳S1的屈曲部分在洞口附近，为局部屈曲。由表2可知：门洞的开设将大幅降低屈曲特征值，S1最低阶的屈曲特征值较S0的降低约21%。此外，对比模型S1~S8可知，随着拱梁截面刚度的增大，网壳的屈曲特征值将缓慢上升，但增长幅度有限。

另外，对比模型S1与S11可知：荷载非对称分布对此切边球壳无不利影响，且各模型各阶屈曲模态对应的特征值较为密集。

4 非线性屈曲分析

对于跨度较大、受荷非对称、存在安装偏差的实际工程，引入初始几何缺陷并按照考虑几何非线性有限元法(即荷载−位移全过程分析)进行计算的非线性屈曲分析方法，比网壳的特征值屈曲分析方法更具有指导意义。若在非线性屈曲分析中不考虑材料的弹性，则为几何非线性屈曲分析；反之，则为双重非线性屈曲分析。几何非线性屈曲分析荷载−位移全过程曲线的控制方程表达式为

TΔΔ−(3)

式中：T为切线刚度矩阵，T=L+G；Δ为位移增量向量；Δ为等效外荷载向量；为等效节点力向量。

4.1 初始几何缺陷模态的影响

实际网壳结构不可避免地存在各种初始缺陷，初始缺陷对网壳结构的稳定性有较大影响，若考虑初始缺陷，则实际网壳结构的稳定承载力将明显低于理想结构的稳定承载力。稳定分析对初始缺陷的选取主要有随机缺陷模态法和一致缺陷模态法[11]。

文献[12]采用特征缺陷模态法考虑初始缺陷的影响，而特征缺陷模态法隶属于一致缺陷模态法的范畴。其第4.3.3条规定：进行网壳全过程分析时应考虑初始几何缺陷(即初始界面曲面形状的安装偏差)的影响，初始几何缺陷分布用结构的最低阶屈曲模态，其最大计算值可按网壳跨度的1/300取值。

对于一致缺陷模态法，初始缺陷分布是一种统计意义上的最不利分布，当初始几何缺陷按最低阶屈曲模态分布时，求得的稳定承载力可能是最不利的。于是，对随机缺陷分布的结构只需按最低阶屈曲模态缺陷分布通过一次非线性计算即可求出可能的临界荷载最小值，使计算量大大减少，这是它的优点[13]。但是，基于几何线性材料弹性假定的特征值屈曲分析，其刚度矩阵建立在结构未受载时的初始构形上，最低阶屈曲模态仅能反映加载的最初阶段结构的变形趋势，故只能作为结构设计的定性估计，缺乏工程实际意义[14]。非线性分析中，结构的位移场和应力场不断地非线性变化，假定小变形不再适用；此外，构件可能进入弹塑性或塑性阶段，最低阶屈曲模态不能反映整个非线性分析过程中的变形趋势，因此，它很可能不是结构的最不利缺陷分布模态[15]。

结合本文研究的切边球壳，由于其壳面已被削弱，其对初始几何缺陷将更敏感，且各模型各阶屈曲模态对应的特征值比较密集，使任意选择在前20阶中的一种屈曲模态作为初始几何缺陷分布模态且均可以产生一条可能的平衡路径，进而求得最不利稳定承载力。因此，对本结构采用“特征缺陷模态法”是不合适的。

综上所述，本结构最不利屈曲模态具有任意性。故本文采用前20阶特征值屈曲模态作为初始几何缺陷分布模态，并取跨度的1/300为初始几何缺陷，在各模型对应的荷载组合下，对所有模型进行几何非线性屈曲分析。表3所示为各模型稳定承载力计算结果。图4所示为模型S1前18阶的荷载−位移曲线。图5所示为模型S0和S2~S11的部分荷载−位移曲线。

表3 稳定承载力系数计算结果

注：有下划线的值为该模型的最不利稳定承载力系数，其对应的模态即为该模型最不利模态。

(a) 1~6阶；(b) 7~12阶；(c) 13~18阶

(a) S0；(b) S2；(c) S3；(d) S4；(e) S5；(f) S6；(g) S7；(h) S8；(i) S9；(j) S10；(k) S11

由表3可知，对于切边球壳，最不利模态均不为最低阶，一致缺陷模态法并不通用。若以最低阶模态作为最不利模态，将高估网壳的稳定承载能力。以实际工程模型S1为例，最不利模态出现在第13阶，稳定承载力系数为5.01，若采用一致模态法时，稳定承载力系数为5.81，高估近16%。这显然是不合理的。

4.2 荷载非对称分布的影响

非对称荷载是导致网壳结构失稳的因素之一，实际工程中几种网壳结构的倒塌均发生在不均匀的荷载下[16]。虽然各种形式的球壳具有极好的空间工作性能，荷载的非对称分布对其稳定承载力几乎没有影响，但是，本文中的切边球壳由于壳面已被削弱，非对称荷载对其是否起控制作用值得研究。

由表3可知：恒载、活载全跨布置时，模型S1最不利模态(第13阶)下的稳定承载力系数为5.01；恒载全跨布置、活载半跨布置时，模型S11最不利模态(第16阶)下的稳定承载力系数为6.35。由此可知，活载非对称布置对此结构并未起控制作用。说明球壳结构即使切边开洞后，依然保持着良好的空间工作性能，对活载的非对称布置并不敏感。

4.3 球壳切边的影响

与完整球壳受力均匀，传力明确等特点相比，切边球壳的受力状况及传力路径将因壳面破坏而受到不良影响，进而降低结构的稳定性能。

由表3可知，切边球壳S1最不利模态(第13阶)下的稳定承载力系数较小，完整网壳S0最不利模态(第12阶)下的稳定承载力系数降低近25%。且前者的用钢量比后者的用钢量增加近20%，可见：球壳的切边将大幅降低结构稳定性能，支承拱梁的设置十分必要，应作为设计要点进行重点关注。

4.4 拱梁截面刚度的影响

切边球壳的支承拱梁主要承担网壳的竖向荷载与水平荷载，以尽量消除壳面削弱对结构静力及稳定性造成的不利影响。仅在外部竖向荷载的作用下，拱梁仍承受较大的水平力，故需考虑其竖向刚度与水平刚度对结构稳定性的影响。此外，经分析，小门拱梁截面刚度的改变对结构稳定性影响很小，因此，本文主要讨论大门拱梁截面对结构稳定性能的影响。

拱梁截面刚度对结构稳定承载力系数的影响见图6。由图6可知，不论是增大拱梁截面的竖向刚度还是增加水平刚度，结构稳定承载力系数均有所增大，但当拱梁的竖向刚度或者水平刚度增大到一定值时，再增大竖向刚度或水平刚度，其对稳定承载力系数的提高也不明显；同时，增大拱梁竖向刚度进而提高切边球壳稳定承载力系数的效益明显大于提高水平刚度带来的效益。因此，在实际工程中，若遇到拱梁刚度较弱进而造成结构稳定性不足时，可优先考虑增加拱梁的竖向刚度。

(a) 截面高度；(b) 截面宽度

4.5 网壳杆件截面刚度的影响

拟壳法基本思想是通过刚度等代的原理，将网壳比拟成光面实体壳[16]。对于完整的网壳结构，网壳杆件截面刚度大的网壳比拟的实体壳厚度较厚，反之，则较薄。在同等条件下，较厚实体壳的稳定性能要优于较薄实体壳的稳定性能。由表3可知：对于切边球壳，杆件截面刚度较大的切边球壳的稳定承载力系数较高。

此外，虽然增大拱梁截面刚度与网壳杆件截面刚度均可提高切边球壳的稳定承载力系数，但对切边球壳稳定性能起主导作用的是网壳杆件截面刚度。在网壳杆件截面刚度较小的情况下，通过增大拱梁截面刚度不能大幅度提高切边球壳稳定承载力系数。只有在保证一定网壳杆件截面刚度的前提下，合理选择拱梁截面刚度，才能找到切边球壳结构设计中的最优解。

另外，根据结构失稳模态、失稳凹陷常常首先发生在门洞附近，特别是两门洞之间，因此，在设计时，此处区域内杆件截面刚度要加强。

4.6 材料弹塑性的影响

为了更准确地反映切边球壳实际工作状况，对结构考虑材料弹塑性的双重非线性屈曲进行分析。

钢材弹塑性屈服准则采用Von Mises屈服准则，考虑钢材具有Bauschinger效应，弹性模量为2.06×105MPa，其弹塑性本构关系采用双直线模型，屈服强度为345 MPa，且符合理想弹塑性假定。模型S1在其最不利模态(第13阶)下的几何非线性与双重非线性荷 载−位移曲线对比图见图7。

1—几何非线性；2—双重非线性

考虑材料弹塑性的非线性屈曲分析中，计算得到模型S1最不利模态(第13阶)下的稳定承载力系数为4.37。几何非线性屈曲分析中，其稳定承载力系数为5.01，下降近13%，但其仍有满足文献[8]要求的安全储备。由此可知，材料的弹塑性性能对切边球壳的稳定性能有较大影响。

4.7 初始几何缺陷的影响

分析模型S1在其最不利模态(第13阶)下，考虑初始几何缺陷分别取跨度的1/300，1/400，1/500，1/600，1/700，1/800，1/900，1/1000，1/1100，1/1200以及无缺陷时，结构的几何非线性屈曲性能，进而探讨切边球壳初始几何缺陷的合理取值。不同初始几何缺陷下的荷载−位移曲线及其对结构稳定承载力的影响分别如图8和9所示。

图8 不同初始几何缺陷下的荷载−位移曲线

图9 初始几何缺陷取值的影响

由图9可知：随着初始几何缺陷的增加，结构的稳定承载力均呈不断下降的趋势。由图9可见：当初始几何缺陷从跨度的1/400变化至1/300时，结构的稳定承载力从5.03下降至5.01，下降率仅为0.40%。说明当初始几何缺陷值取为跨度的1/400时，其对结构的不利影响已经得到充分体现。因此，在实际工程中，类似结构的始何几何缺陷取值可适当放宽。

另外，结构无缺陷时的稳定承载力系数为14.78，初始几何缺陷取跨度1/300时的稳定承载力系数为5.01，降低了近66%。再结合图9中曲线较陡的斜率可知，切边网壳对初始几何缺陷较敏感。

5 结论

1) 球壳的切边将大幅度降低结构的屈曲特征值，失稳形态从完整网壳的整体失稳转变为洞口附近的局部失稳。结构的稳定承载力系数也随着门洞的开设而大幅度减小。

2) 拱梁截面刚度和网壳杆件截面刚度的增加均能提高结构的稳定承载力系数。但是，后者才是改善本结构稳定性能的主要途径。

3) 由特征缺陷模态法求得的稳定承载力系数往往不是最小。本结构的最不利稳定承载力系数出现在第13阶，比特征缺陷模态法求得的稳定承载力系数降低近16%。

4) 本结构对初始几何缺陷较为敏感，但当初始几何缺陷值取为跨度的1/400时，其影响已能得到充分体现。故在实际工程中，类似结构的始何几何缺陷取值可适当放宽。

5) 材料弹塑性是影响该结构稳定性能的主要因素之一，考虑材料非线性的双重非线性稳定承载力系数明显低于几何非线性稳定承载力系数。

6) 荷载不对称分布对本单层球壳结构并无不利影响。

[1] Yamada S, Takeuchi A, Tada Y, et al. Imperfection-sensitive overall buckling of single-layer latticed domes[J]. Journal of Engineering Mechanics, 2001, 127(4): 382−386.

[2] Kato S, Kim J M, Cheong M C. A new proportioning method for member sections of single layer reticulated domes subjected to uniform and non-uniform loads [J]. Engineering Structures, 2003, 25(10): 1265−1278.

[3] Abedi K, Shekastehband A. Static stability behaviour of plane double-layer tensegrity structures[J]. International Journal of Space Structures, 2008, 23(2): 89−102.

[4] Mohammadi M, Abedi K, Taghizadieh N. Stability Analysis of Single-Layer Barrel Vault Space Structures[J]. International Journal of Space Structures. 2012, 27(4): 203−218.

[5] 罗永峰, 沈祖炎, 胡学仁. 单层网壳结构弹塑性稳定试验研究[J]. 土木工程学报, 1995, 28(4): 33−40.
LOU Yongfeng, SHEN Zuyan, HU Xueren. Experimental study on elasto-plastic stability of single layer reticulated shells[J]. China Civil Engineering Journal, 1995, 28 (4): 33−40.

[6] 沈世钊. 网壳结构的稳定性[J]. 土木工程学报, 1999, 32(6): 11−19.
SHEN Shizhao. Stability of reticulated shell structures[J]. China Civil Engineering Journal, 1999, 32(6): 11−19.

[7] 曹正罡, 范峰, 沈世钊. 单层球面网壳的弹塑性稳定性[J]. 土木工程学报, 2006, 39(10): 6−10.
CAO Zhenggang, FAN Feng, SHEN Shizhao. Elasto-plastic stability of single-layer reticulated domes[J]. China Civil Engineering Journal, 2006, 39(10): 6−10.

[8] 范峰, 严佳川, 曹正罡. 考虑杆件失稳影响的网壳结构稳定性研究[J]. 土木工程学报, 2012, 45(5): 8−17.
FAN Feng, YAN Jiachuan, CAO Zhenggang. Study on stability of reticulated shell structures considering the influence of member buckling[J]. China Civil Engineering Journal, 2012, 45(5): 8−17.

[9] 景辉, 杨会杰, 金来建, 等. 榆林科技馆单层带缺口球壳结构设计[J]. 建筑结构, 2010, 40(12): 86−88.
JING Hui, YANG Huijie, JIN Laijian, et al. Structural design of reticulated shell of Yulin science and technology museum[J]. Building Structure, 2010, 40(12): 86−88.

[10] 沈晓明, 舒赣平. 不规则划分单层网壳结构稳定性分析[J]. 建筑结构, 2009, 39(S1): 101−104.
SHEN Xiaoming, SHU Ganping. Stability analysis of single layer lattice shell with irregular division[J]. Building Structure, 2009, 39(S1): 101−104.

[11] 沈世钊, 陈昕. 网壳结构稳定性[M]. 北京: 科学出版社, 1999.
SHEN Shizhao, CHEN Xin, Stability of latticed shell structures[M]. Beijing: Science Press, 1999.

[12] JGJ 7—2010, 空间网格结构技术规程[S].
JGJ 7—2010, Technical specification for space frame structures[S].

[13] 姜正荣, 石开荣, 徐牧, 等. 某椭圆抛物面辐射式张弦梁结构的非线性屈曲及施工仿真分析[J]. 土木工程学报, 2011, 44(12): 1−8.
JIANG Zhengrong, SHI Kairong, XU Mu, et al. Analysis of nonlinear buckling and construction simulation for an elliptic paraboloid radial beam string structure[J]. China Civil Engineering Journal, 2011, 44(12): 1−8.

[14] 张爱林, 刘学春. 奥运羽毛球馆张弦穹顶基于整体稳定的优化设计[J]. 建筑结构, 2007, 37(2): 1−5.
ZHANG Ailin, LIU Xuechun. Suspend-dome optimal design of Olympic badminton stadium based on integral stability[J]. Building Structure, 2007, 37(2): 1−5.

[15] 葛家琪, 张国军, 王树, 等. 2008 奥运会羽毛球馆弦支穹顶结构整体稳定性能分析研究[J]. 建筑结构学报, 2007, 28(6): 22−30, 44.
GE Jiaqi, ZHANG Guojun, WANG Shu, et al. The overall stability analysis of the suspend-dome structure system of the badminton gymnasium for2008 Olympic games[J]. Journal of Building Structures, 2007, 28(6): 22−30, 44.

[16] 张毅刚, 薛素铎. 大跨空间结构[M]. 北京: 机械工业出版社, 2005.
ZHANG Gangyi, XUE Suduo. Space structures with large span[M]. Beijing: China Machine Press, 2005.

Nonlinear buckling analysis for a trimmed irregularKiewitt single-layer spherical shell structure

HE Sheng1, CHEN Qingjun1, 2, 3, JIANG Zhengrong1, 2, LAI Hongtao4, LIU Hongliang1

(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510641, China;2. State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou 510641, China;3. Centre for Infrastructure Engineering and Safety, The University of New South Wales, UNSW Sydney, 2052, Australia;4. Architecture Design & Research Institute, South China University of Technology, Guangzhou 510641, China)

The nonlinear buckling behavior of a trimmed irregular Kiewitt single-layer spherical shell structure was investigated by introducing the irregularity caused by the openings of the dome, the changes of vertical and horizontal stiffness of the support arch beams, unsymmetrical distribution of live loads, initial geometric imperfection, geometric nonlinearity and material elastic-plasticity. The nonlinear load-displacement whole process of this structure was analyzed by using the finite element software ANSYS. The results show that compared with perfect spherical latticed shell, the stability of this trimmed spherical shell is considerably reduced. The vertical stiffness of the support arch beams has greater influence on the stability of this structure than the horizontal stiffness. Using the consistent imperfect buckling analysis method, the coefficient of stable bearing capacity usually is not minimal. A 1 /400 of the span can be appropriately taken as the maximum value of initial geometric imperfection. The material nonlinearity might have significant effects on the stability of this trimmed spherical shell. The unsymmetrical distribution of live loads does not have adverse impact on the stability of the structure.

irregular edges; Kiewitt spherical latticed shell; openings; nonlinear buckling; initial geometric imperfection

TU393.3

A

1672−7207(2015)02−0701−09

2014−03−07；

2014−06−20

中央高校基本科研业务费专项资金资助项目(2014ZZ0026, 2011ZM0115)；华南理工大学亚热带建筑科学国家重点实验室课题(2013ZC19，2012KB30)；广东省自然科学基金资助项目(10451064101005087)(Projects (2014ZZ0026,2011ZM0115) supported by the ‍Fundamental Research Funds for the Central Universities; Projects (2013ZC19, 2012KB30) supported by the State Key Lab of Subtropical Building Science, South China University of Technology; Projects (10451064101005087)‍ supported by the Natural Science Foundation of Guangdong Province, China)

陈庆军，博士，副教授；从事结构理论、结构仿真分析等研究；E-mail：qjchen@scut.edu.cn

10.11817/j.issn.1672-7207.2015.02.044

(编辑 赵俊)