基于能量法的高承台桩基沉降计算方法

赵明华，杨雨晴，尹平保，龙军



基于能量法的高承台桩基沉降计算方法

赵明华1，杨雨晴1，尹平保2，龙军1

(1. 湖南大学 岩土工程研究所，湖南 长沙，410082；2. 长沙理工大学 土木与建筑学院，湖南 长沙，410004)

为探讨高承台桩基的沉降计算方法，考虑高承台群桩中各基桩的相互作用，首先基于Cooke原理推导得到基桩桩侧单位厚度土的等效刚度系数；其次，从能量传递的角度建立承台−桩基的平衡方程，并联立承台−桩基变形协调关系以及桩端边界条件，利用能量法对基桩桩身轴力与位移进行求解，从而得到高承台桩基沉降计算方法，编制相应的计算程序。最后，利用该方法及计算程序对某工程中的高承台桩基进行计算。研究结果表明：采用本文方法所得计算结果与实测结果较吻合，验证了本文计算方法的合理性。

桥梁工程；高承台桩基；能量法；等效刚度系数；沉降

群桩沉降计算是桩基工程设计中的一大难题。桩的几何尺寸、桩周岩(土)体类别与性质、桩间距以及所受荷载与持续时间等都将对沉降计算结果产生很大影响[1]。目前，有关群桩沉降计算的方法主要有等代墩基法、等效分层总和法及弹性理论法等[2−6]。其中，等代墩基法是将基桩和承台范围内的桩间土看成为一个整体，即相当于1个布置在天然地基上的深基础，而按扩展基础来计算沉降。该法虽然考虑了桩群外围尺寸和桩长的影响，却忽视了桩数、桩径以及桩间距等因素的影响。关于等效作用分层总和法，其主要是引入等效沉降系数，将Boussinesq解与Mindlin解联立起来求解桩基沉降，其除考虑群桩几何特性的影响外，还可将计算结果编制成表格，便于工程应用。但该系数为一经验系数，与现有桩基工程沉降实测资料的积累有关，且难以考虑持力层、土层剖面和压缩性等因素的影响。可见上述2种方法均无法考虑桩间土体压缩变形的影响，故不宜用于桩间距大于6倍桩径的群桩。至于弹性理论法，其主要适用于桩间距较大、桩长不一以及布桩不规则的群桩。由于忽略桩群在土中的“加筋效应”和“遮帘效应”，即未考虑桩的存在所带来的影响，因而对某些加工硬化型土如非密实的粉土、砂土可能会引起较大的偏差。总之，群桩沉降计算方法虽多，但各有不同的适用范围。受水文地质条件以及实际工程环境等因素的影响，对于某些大桥或特大桥，其基础绝大多数采用高承台群桩。在高承台群桩基础中，各基桩主要通过桩侧摩阻力与桩端阻力将竖向荷载传递给地基土与邻近桩基，由此产生的应力重叠效应改变了基桩和土体的受力状态，反过来，这种效应又将进一步影响基桩桩侧摩阻力和桩端阻力的发挥。对于高承台桩基，目前国内外已有一些学者对桩土相互作用机理及荷载传递规律进行了研究[7−9]，但涉及高承台群桩沉降计算的研究不是很多。高承台群桩基础荷载传递异常复杂，现有的基桩沉降计算方法具有一定局限性，很有必要在前人研究的基础上，深入探讨考虑桩−土−桩相互作用的高承台桩基沉降计算方法。文献[10]将能量法应用于单桩沉降的计算，取得了一定成果。本文作者以此为基础，首先引入Cooke原理[11−12]，考虑群桩中桩−土−桩的相互作用，导出各基桩的桩侧土体等效刚度系数；其次，利用能量法，对高承台桩基平衡方程进行分析求解，从而得到一种高承台桩基沉降计算方法；最后，以某实际工程中高承台桩基为例，利用上述方法进行计算。

1 高承台桩基沉降计算

1.1 计算模型

承台在上部结构荷载的作用下产生变形，群桩中的基桩桩侧摩阻力可采用佐藤悟提出的桩侧摩阻力与桩土相对位移弹塑性模型进行计算[10]，如图1所示。其中：f，f和f分别为桩侧土体的极限摩阻力、桩侧土层达到极限摩阻力f的最小桩土相对位移、桩侧土层的摩阻力传递系数，ff/f。

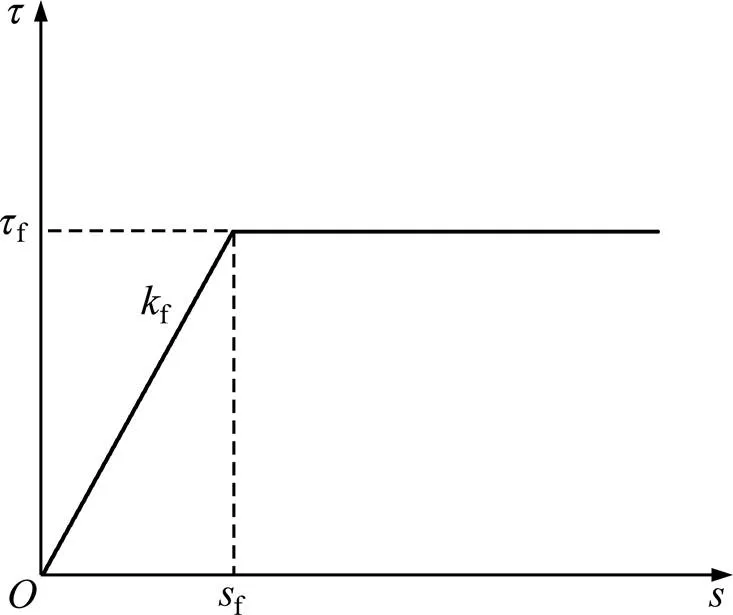
图1 桩侧摩阻力传递模型

受群桩效应的影响，群桩中各基桩桩侧摩阻力系数k与单桩桩侧摩阻力传递系数f不同。根据Cooke原理，假设高承台桩基中的基桩数为，且桩身均位于均质土中，桩材、桩径以及入土深度也均相同。桩−桩相互作用示意图如图2所示。以群桩中的桩(=1，2，3，…，)为例，桩桩侧单位厚度土的等效刚度系数k为

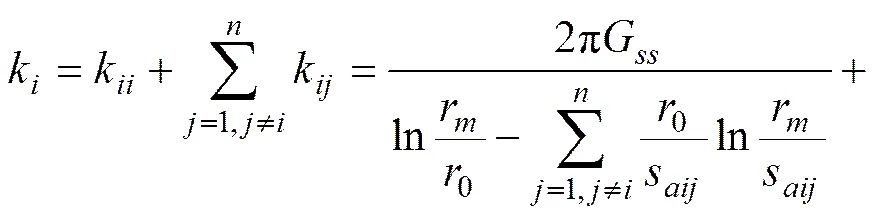
式中：k为桩顶部作用荷载发生沉降时桩受周围桩群影响从而产生的桩侧单位厚度土的等效刚度系数；k为桩顶部受力发生沉降时桩受其影响从而产生的桩侧单位厚度土的等效刚度系数；0为桩的截面半径；s为桩和桩的桩间距；G为桩侧土体的剪切模量；r为位移影响半径，根据文献[13]，可取r=2.5(1−)；为不均匀系数；为桩间土体的泊松比；H为桩身入土段长度。

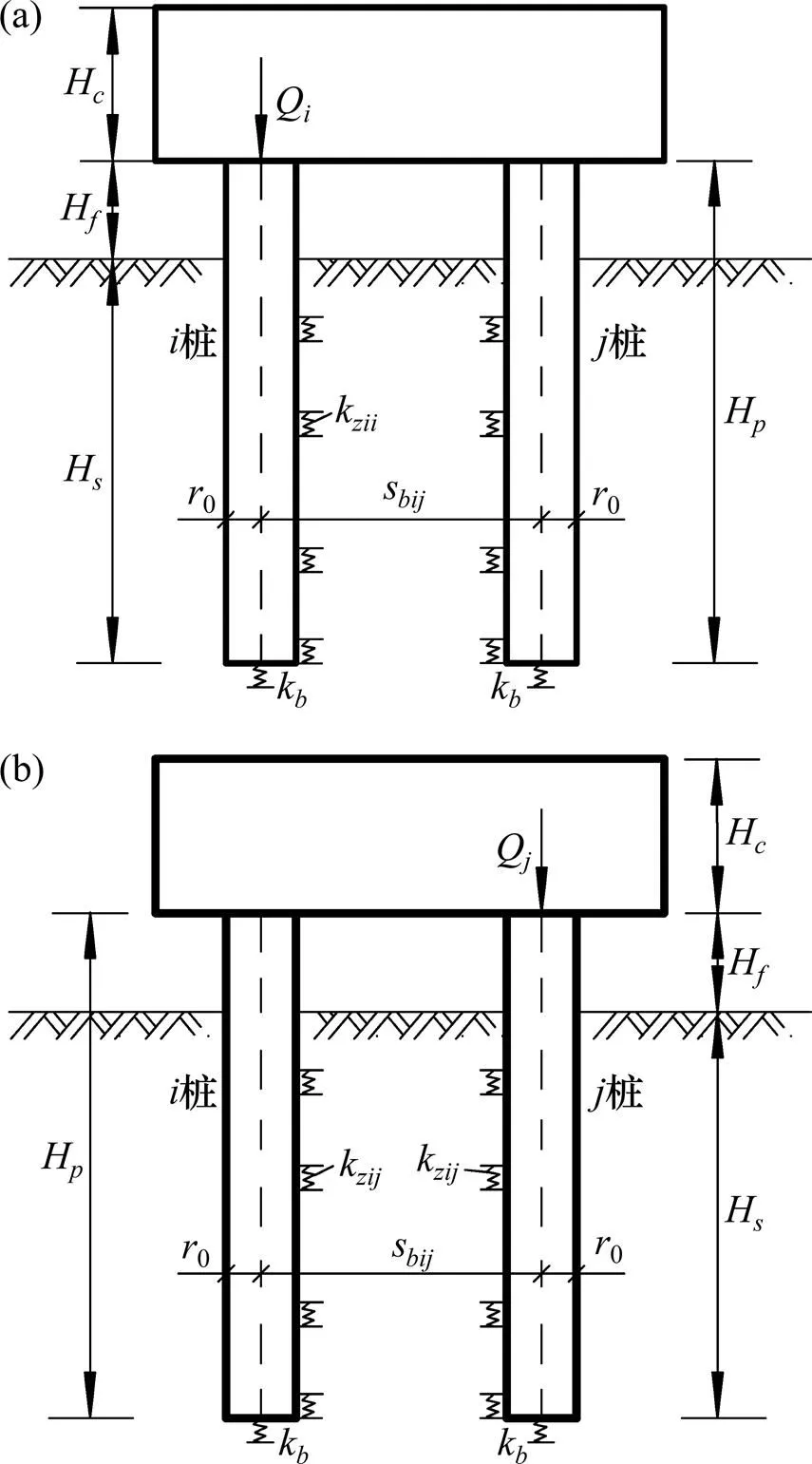
(a) i桩对j桩的作用；(b) j桩对i桩的作用

1.2 能量法求解

为便于后续分析及简化推导过程，进行如下假定：

1) 桩身处于弹性变形阶段，且不发生屈曲变形；

2) 桩侧摩阻力先于桩端阻力发挥[10]。

根据能量原理，可知高承台桩基在地基中的总势能增量Δ由桩身变形能W、沉降引起的桩身势能增量W1和承台势能增量W2组成，即

式中：H为桩身总长；Δ1为基桩重心的位移；Δ2为承台重心的位移；E为桩身弹性模量；A为桩身截面积；N()为桩深度处桩身轴力；M为承台质量；M为桩桩身质量；为重力加速度；s为桩桩端位移；δ为桩桩身变形。根据变形协调原理，取1~时，s+δ都相等。

引起承台−桩总势能发生改变的原因在于外力作功，即承台顶部荷载作功W、桩侧摩阻力作功W和桩端阻力作功W。则桩身总势能增量Δ可表示为

式中：为承台顶荷载；p为桩桩端阻力；s=δ+s，为桩桩顶位移；s为桩桩端位移；τ()为桩深度处桩侧摩阻力。

1.3 桩基沉降计算

1.3.1 桩身悬臂段沉降

对于高承台桩基中的悬臂段，由于没有受桩侧土体的影响，悬臂段的沉降即为该桩段的桩身压缩变形，其可由下式求得：

式中：p为桩桩顶荷载；H为桩身悬臂段长度。

1.3.2 桩身入土段沉降

对于桩基的入土段，设桩桩顶荷载为p，则可建立相应的能量平衡方程：

将式(3)，(4)，(7)~(9)代入式(11)可得

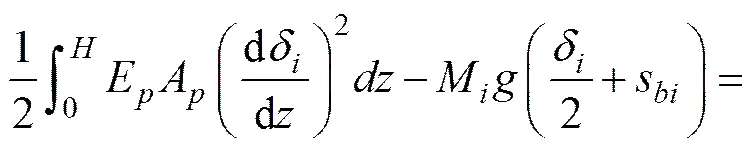
式中：s为桩桩身入土段的总沉降量。

式(12)即为以整个桩身为对象的总的能量平衡方程。若将桩桩身分为个连续的单元，如图3所示，则对于第单元 (=1，2，3，…，)有

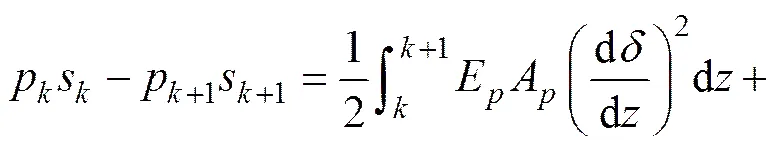
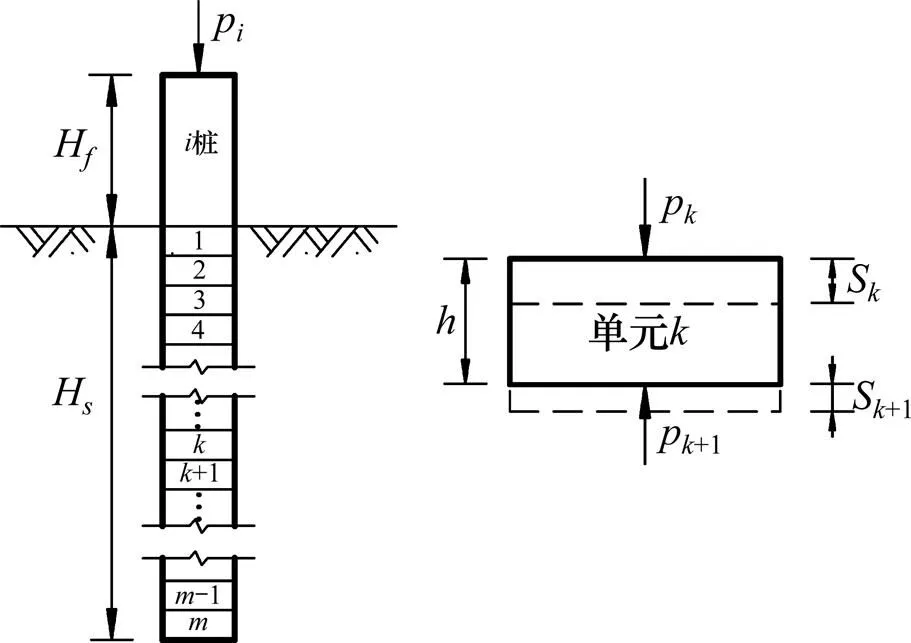
(a) 单元划分；(b) 单元受力

式中：m为基桩第单元质量，s为第单元顶部位移；s1为第单元底部位移。如图3所示，基桩第单元的桩身变形d为：

将式(14)和式(15)代入式(13)可得

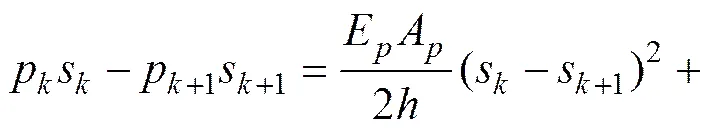
式中：为桩身截面周长；每个单元高度=H/；为单元个数；H为桩身入土段长度。式(16)可进一步改写为

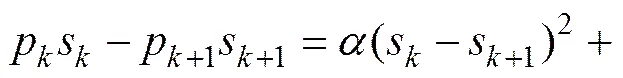
式(18)和式(19)即为第单元顶部与底部的轴力计算式。由式(18)可得s+1的计算式为

若忽略由于第单元弹性变形引起的单元顶部与底部的摩阻力差异，考虑群桩下其他基桩对桩桩侧土体的影响，则将桩桩侧单位厚度土体的等效刚度系数代入式(20)可得：

式中：τ为桩身第单元侧边土体的极限摩阻力；s为桩身第单元侧边土层达到极限摩阻力的最小相对位移。根据桩端边界条件，第单元(桩端)底部的轴力p又可表示为

式中：k为桩端阻力传递系数；q为桩端阻力极限值；ξ桩端土体达到极限阻力q的最小桩端土体位移。已知承台顶部荷载，对刚性高承台群桩，各桩桩顶沉降s(=1，2，3，…，)相同，承台顶部荷载由各桩共同承担，即可建立以下方程组：

联立上述方程组，并结合前面的沉降计算公式，即可求得高承台桩基入土段的总沉降。

1.3.3 桩顶总沉降

高承台桩基的桩顶总沉降为

s=δ+s(26)

式中：s为高承台桩基的桩顶总沉降；s为桩身入土段的总沉降量。

2 沉降计算步骤及流程

根据上述计算方法可利用Matlab编制相应的计算程序。现以4桩高承台桩基为例，对计算程序进行简单说明(沉降计算流程图见图4)。

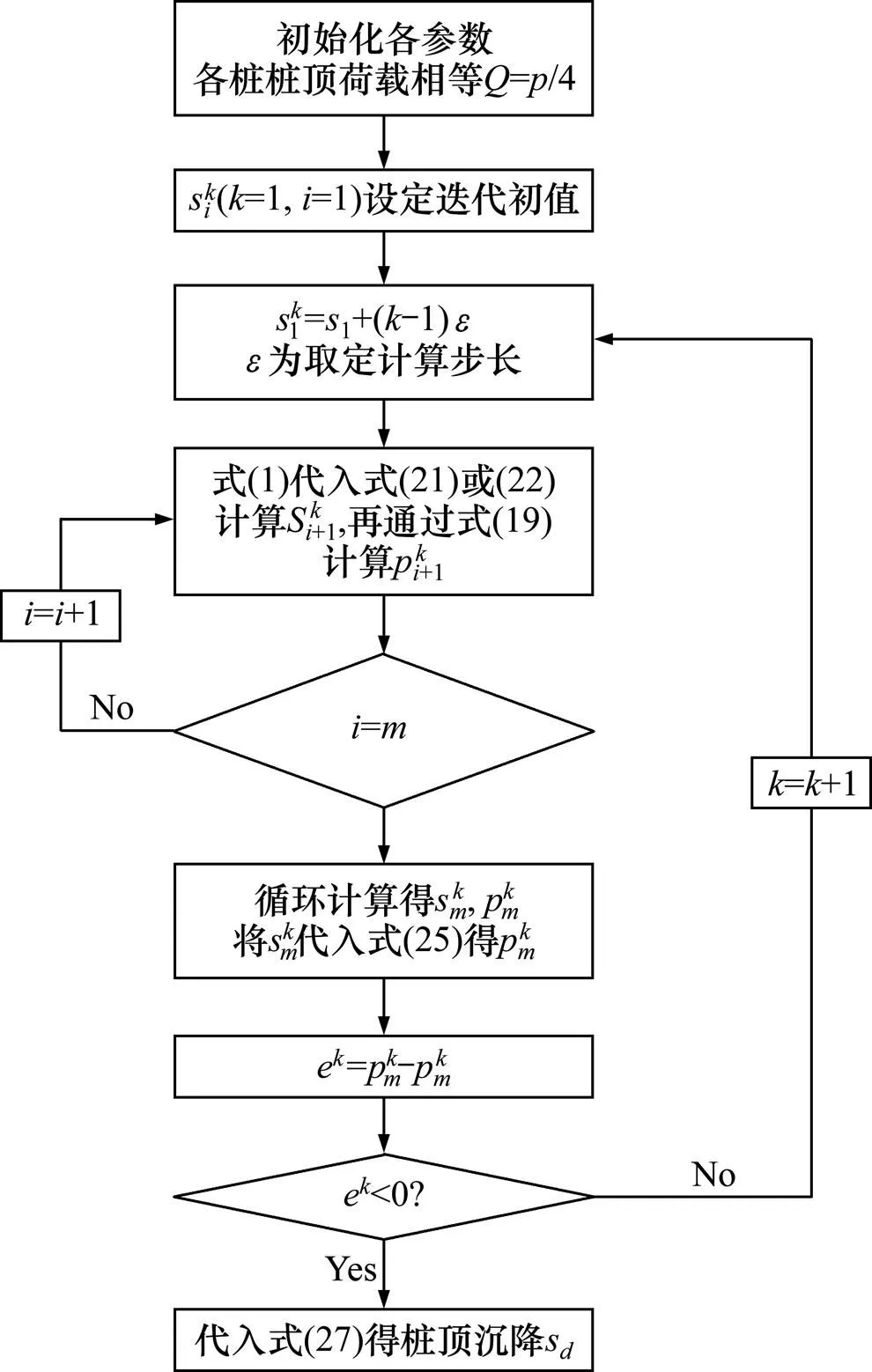
图4 沉降计算流程图

设定承台顶荷载，桩侧各土层参数H，τ，s和k等计算参数初始化数值。程序对入土段桩顶沉降s设初始值。计算中将以一定步长搜索整个s的定义域，并在找到满足桩端边界条件的s时停止。算法步骤和逻辑图具体如下。

1) 程序设置初始化，对计算常量赋值，包括各土层土性参数、土层厚度、单元高度、承台顶部荷载等。

2) 对于4桩承台，由其受力完全对称，则可简化为对单桩进行分析。通过式(25)可得桩顶荷载p=/4(=4，为群桩桩数)。

3) 对s(为迭代次数，为桩身微单元数，=l，=1)设定迭代初始值(一般可取0.2 mm)。

4) 将式(1)代入式(21)或(22)计算s+1；由式(19)计算p+1。

5) 重复步骤4)，直至得出s和p为止。

6) 将s代入式(25)，得到′。

7) 计算e=p-’,若e>0，则进入步骤8)；若e<0，则进入步骤9)。

8) 增加s1个步长值，可根据误差梯度调节取值，此处建议取较小常量0.1 mm，此时，s1=s+，进入步骤3)。

9) 当e＜0，e−1＞0时，搜寻到满足边界条件的迭代值，此时桩顶沉降s取值为

3 工程算例

引用文献[14]中苏通长江大桥主桥南塔桥梁桩基工程的实测数据，与本文方法所得计算结果进行比较分析。该工程群桩基桩总长为114 m，其中入土深度为75.00 m，桩径为2.50 m，桩间距为6.25 m(2.5倍桩径)。工程地质概况如表1所示，其他参数见文献[14]。2×2与3×3群桩沉降计算结果分别见图5和图6。

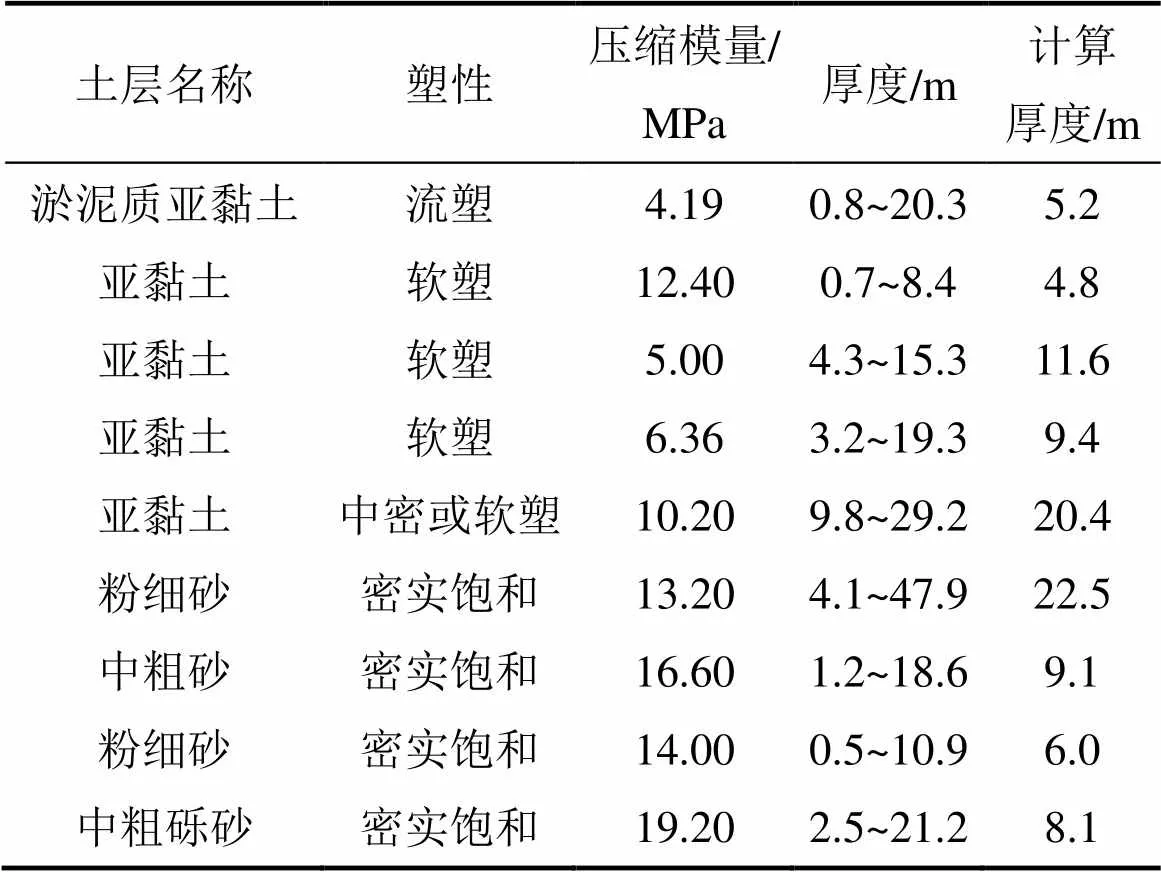
表1 桩基工程地质表

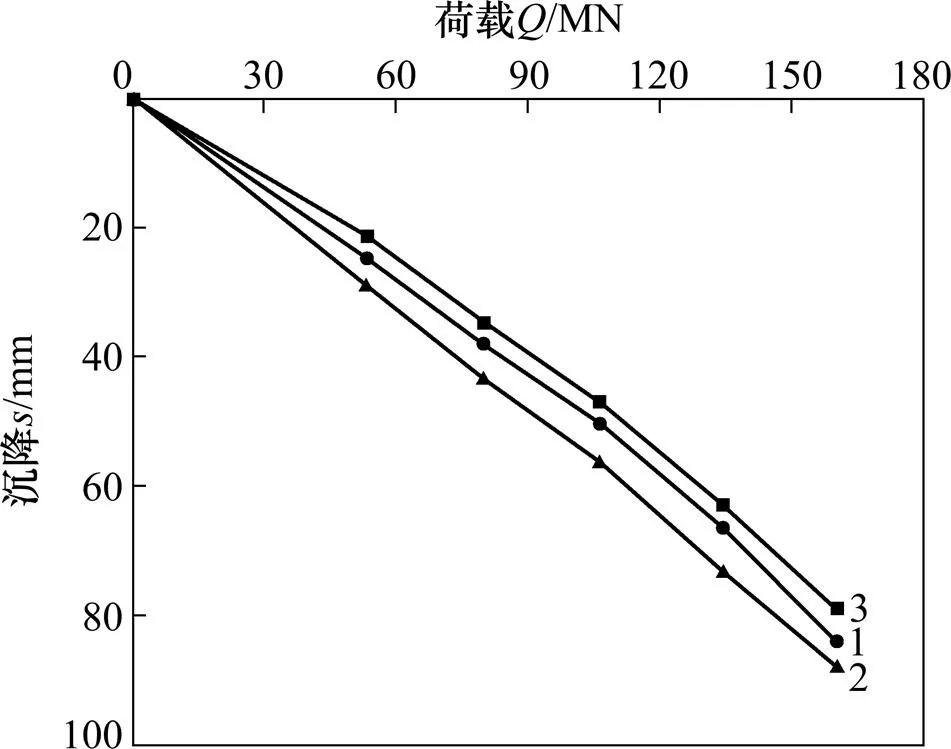
1—本文值；2—文献[14]中值；3—试验值

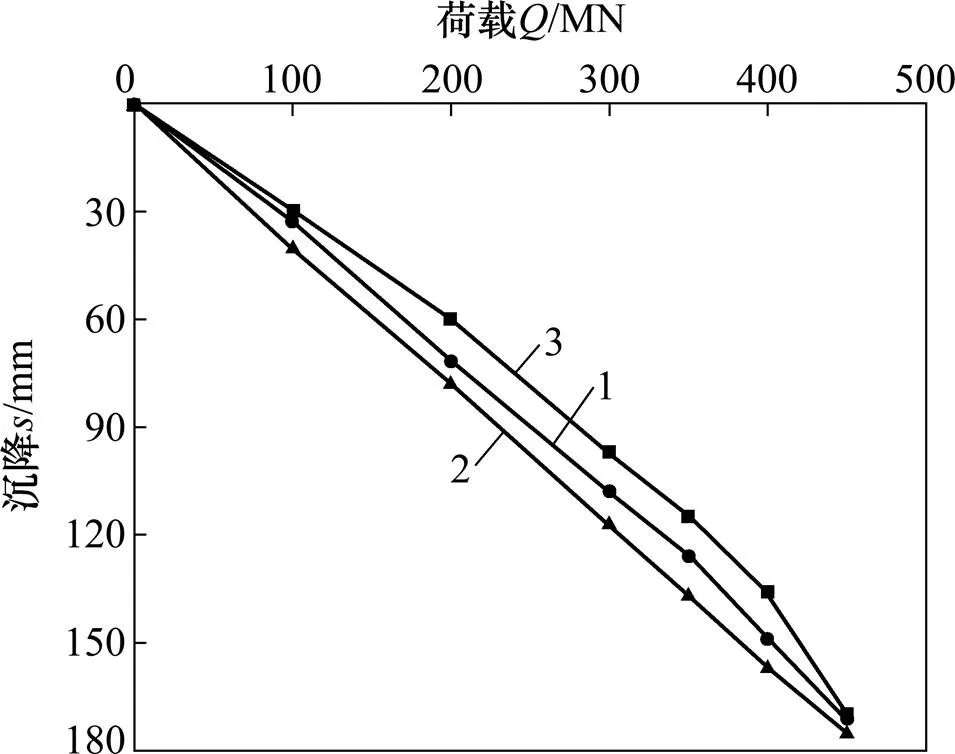
1—本文值；2—文献[14]中值；3—试验值

由图5和图6可知：本文方法得到的计算结果与2×2和3×3群桩在全注浆最大冲刷深度工况条件下的实测值以及文献[14]的计算结果均较吻合，验证了本文计算方法及程序的可靠性。由于在实际工程中各基桩之间相互作用影响程度随桩侧土体均匀度的减小而减弱，故本文计算结果较实测值稍偏大，对2×2群桩最大相对误差为12.6%；而3×3群桩的最大相对误差为15.1%，其计算精度尚在可接受范围内。计算误差的产生是因为计算方法受线性约束，计算程序反复迭代，也可带来误差积累，从而导致本文计算值与实测值不吻合。关于超大荷载区段的算法优化工作，有待进一步研究。

4 结论

1) 利用Cooke原理导出高承台桩基桩侧的等效刚度系数，并利用能量法对承台−桩基平衡方程进行求解，进而提出了高承台桩基沉降计算方法。

2) 根据本文计算方法编制了相应的计算程序，利用该程序计算某实际工程的桥梁桩基。对比分析表明：计算值与实测值及文献值均较吻合，验证了本文计算方法的可靠性。该方法可为高承台桩基工程的设计计算提供一种行之有效的新思路。

3) 超大荷载区段的高承台桩基沉降计算由于受反复迭代引起的误差积累以及计算方法线性约束等因素的影响，其计算值与实测值不吻合，因此，算法优化有待进一步研究。

[1] 《桩基工程手册》编写委员会. 桩基工程手册[M]. 北京: 中国建筑工业出版社, 1995: 164−165.
Committee for Compiling the Pile Foundations Handbook. Pile foundations handbook[M]. Beijing: China Architecture and Building Press, 1995: 164−165.

[2] 何思明, 卢国胜, 廖祖伟. 群桩沉降计算理论分析[J]. 岩土力学, 2003, 24(3): 435−441.
HE Siming, LU Guosheng, LIAO Zuwei. Analysis of settlement of group piles[J]. Rock and Soil Mechanics, 2003, 24(3): 435−441.

[3] 潘时声, 侯学渊. 桩的刚度计算[J]. 岩土工程学报, 1996, 18(1): 1−6.
PAN Shisheng, HOU Xueyuan. Computation of pile head stiffness[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(1): 1−6.

[4] 潘时声. 用分层积分法分析桩的荷载传递[J]. 建筑结构学报, 1999, 20(5): 68−79.
PAN Shisheng. Load transfer analysis of piles by layered integration method[J]. Journal of Building Structures, 1999, 20(5): 68−79.

[5] 房卫民, 赵明华, 苏检来. 由沉降量控制桩竖向极限承载力的分析[J]. 中南公路工程, 1999, 24(2): 23−25.
FANG Weimin, ZHAO Minghua, SU Jianlai. Analysis of predicting vertical limit bearing capacity by the pile settlement[J]. Central South Highway Engineering, 1999, 24(2): 23−25.

[6] 赵明华. 桥梁桩基计算与检测[M]. 北京: 人民交通出版社, 2000: 40−44.
ZHAO Minghua. Calculation and detecting for pile foundations of bridges[M]. Beijing: China Communications Press, 2000: 40−44.

[7] 汪优, 刘建华, 王星华, 等. 软土地层桥梁群桩基础桩土共同作用性状的非线性有限元分析[J]. 岩土力学, 2012, 33(3): 945−951.
WANG You, LIU Jianhua, WANG Xinghua, et al. Nonlinear finite element analysis of pile-soil interaction of bridge pile group foundation in soft soil stratum[J]. Rock and Soil Mechanics, 2012, 33(3): 945−951.

[8] 汪优, 王星华, 刘建华, 等. 软土地层桥梁群桩基础沉降模型[J]. 中南大学学报(自然科学版), 2012, 43(3): 1098−1106.
WANG You, WANG Xinghua, LIU Jianhua, et al. Settlement model of bridge pile group foundation in soft soil stratum[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 1098−1106.

[9] 刘杰, 张可能. 刚性承台下柔性群桩和桩周土荷载传递规律研究[J]. 土木工程学报, 2004, 37(7): 82−87.
LIU Jie, ZHANG Keneng. Study on transferring foundation of load of grouped flexible piles and soil surrounding pile beneath the rigid cap of pile[J]. China Civil Engineering Journal, 2004, 37(7): 82−87.

[10] 刘思思, 赵明华, 言志信. 单桩竖向荷载-沉降曲线的能量法数值计算[J]. 公路交通科技, 2010, 27(8): 22−26.
LIU Sisi, ZHAO Minghua, YAN Zhixin. Numerical calculation of pile vertical load-settlement curve based on energy method[J]. Journal of Highway and Transportation Research and Development, 2010, 27(8): 22−26.

[11] 史佩栋. 实用桩基工程手册[M]. 北京: 中国建筑工业出版社, 1999: 137−140.
SHI Peidong. Practical pile foundations handbook[M]. Beijing: China Architecture and Building Press, 1999: 137−140.

[12] 赵明华, 邹丹, 邹新军. 基于荷载传递法的高承台桩基沉降计算方法研究[J]. 岩石力学与工程学报, 2005, 24(13): 2310−2314.
ZHAO Minghua, ZOU Dan, ZOU Xinjun. Settlement calculation of pile foundations with elevated caps by load transfer method[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(13): 2310−2314.

[13] Randolph M F, Wroth C P. An analysis of vertical deformation of pile groups[J]. Geótechnique, 1979, 29(4): 423−439.

[14] 邓友生, 龚维明. 考虑桩身压缩的高承台超长群桩沉降计算[J]. 工程勘察, 2008(1): 25−27.
DENG Yousheng, GONG Weiming. Settlement calculation of consideration of pile foundations with elevated caps and super-long pile group[J]. Geotechnical Investigation and Surveying, 2008(1): 25−27.

Settlement calculation of pile foundations with elevated caps by energy method

ZHAO Minghua1, YANG Yuqing1, YIN Pingbao2, LONG Jun1

(1. Institute of Geotechnical Engineering, Hunan University, Changsha 410082, China;2. School of Civil Engineering and Architecture,Changsha University of Science and Technology, Changsha 410004, China)

In order to investigate the computational methods for settlement of high-cap pile, an identical stiffness coefficient of surrounding soil with unit thickness was derived based on Cooke principle to simulate the interaction among each pile of pile group. Equilibrium equation of cap-pile was constructed in the viewpoint of energy transmission. Deformation compatibility of cap-pile and boundary conditions at pile end were incorporated to solve axial forces and displacements of pile by using energy approach. Thus a novel calculation method for settlement of pile foundation with high cap was developed and the corresponding program was written. Finally, this method and program was utilized to calculate a high-cap pile in an engineering project. The results show that the results computed by this technique are in accordance with those measured, which verifies the reasonability of this method.

bridge engineering; pile foundation with elevated caps; energy method; equivalent stiffness coefficients; settlement calculation

TU473.1

A

1672−7207(2015)02−0670−06

2014−01−22；

2014−04−25

国家自然科学基金资助项目(51278187)(Project(51278187) supported by the National Natural Science Foundation of China)

赵明华，教授，博士生导师，从事桩基础及软土地基处理等研究；E-mail：mhzhaohd@21cn.com

10.11817/j.issn.1672-7207.2015.02.040

(编辑 陈灿华)