基于形状记忆合金被动减振的飞轮控制系统非线性振动分析

鄂加强，王景阳，钱承，王曙辉，刘腾，蔡皓



基于形状记忆合金被动减振的飞轮控制系统非线性振动分析

鄂加强1, 2，王景阳2，钱承2，王曙辉1, 2，刘腾2，蔡皓1, 2

(1. 湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙，410082；2. 湖南大学 机械与运载工程学院，湖南 长沙，410082)

为减小飞轮控制系统工作时产生的振动影响，采用形状记忆合金被动减振方式构建飞轮控制系统及其动力学模型，对飞轮控制系统被动减振机理进行分析。研究结果表明：基于形状记忆合金被动减振的飞轮控制系统的振幅随着记忆合金弹簧−阻尼结构阻尼的增加而明显减小；在不同频率下，基于记忆合金弹簧−阻尼结构的被动减振飞轮控制系统模型的振动幅值要比非减振飞轮控制系统模型振动幅值降低明显，且具有较好振动衰减效果。

飞轮控制系统；被动减振；形状记忆合金；非线性分析；振动

飞轮控制系统因其耗能小、控制精度高、使用寿命长、无污染等优点而被广泛应用于卫星姿态控制。飞轮一般尺寸较大，且固连在航天器上，主要通过转子的高速旋转来达到储能调姿的作用。但由于存在机械制造误差，会导致飞轮转子产生一定的不平衡量。通过各种方法虽然可以减小不平衡量，但是无法从根本上予以消除，因此，转子的动不平衡问题是不可避免的。转子在启停以及稳定运转过程中会产生不平衡力或者力矩，使转子出现受迫振动。飞轮的结构挠性有可能使飞轮系统与转子高速旋转产生的高频激励产生谐振，增大飞轮系统的振动程度[1]。飞轮的支撑部件是转子激励和航天器响应的中间传递环节，其振动效应也不容忽视，目前主要采取的支撑方式有磁悬浮支撑和机械支撑，特别是采用滚动轴承时，由于摩擦力矩也会使飞轮产生扰动[2−3]，飞轮多采用无刷直流电机作为驱动电机，电机的电磁特性会影响控制力矩的准确输出，使飞轮产生高频振动[4]。由于飞轮系统与航天器固连，飞轮系统的振动会直接传递到航天器上，影响一些精密仪器的工作精度。飞轮工作时产生的扰动是影响有效载荷工作的主要扰动源[5−6]，因此，如何对飞轮工作时产生的振动进行衰减控制和隔离十分重要[7−8]。国内外学者对此进行了大量研究[7−9]，其减振措施较有效，但仍存在一定的局限性。Ti-Ni系形状记忆合金是近年来一种最有发展前途的高性能减振材料，并具有很优的循环性能[10−11]。为此，本文作者采用Ti-Ni系形状记忆合金材料减少飞轮控制系统工作时产生的振动向有效载荷传递，并揭示飞轮控制系统的被动减振非线性程度。飞轮控制系统动力学分析和减振实验效果验证了Ti-Ni系形状记忆合金材料用于飞轮控制系统减振的有效性和可行性。

1 基于形状记忆合金被动减振的飞轮控制系统非线性振动模型

1.1 飞轮控制系统结构设计

飞轮控制系统采用形状记忆合金作为减振材料的被动减振方式，结构如图1所示。飞轮控制系统与连接架固定，飞轮控制系统工作时产生的振动直接传递到连接架，连接架下端与舱壁之间通过记忆合金圈隔开，以减少振动向舱壁传递。连接架的上端采用弹簧和记忆合金与舱壁连接，通过弹簧和记忆合金来吸收连接架的振动。

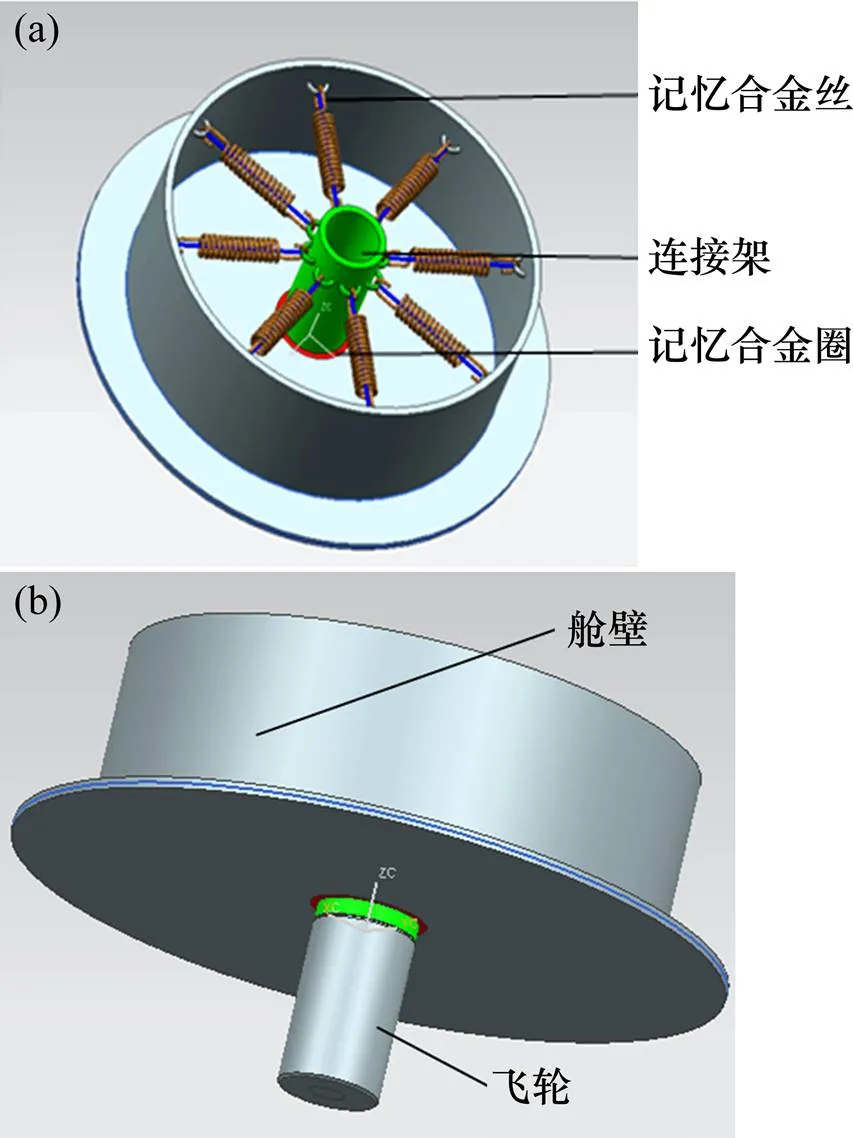
(a) 视图1；(b) 视图2

1.2 基于形状记忆合金被动减振的飞轮控制系统非线性振动模型的建立

由于形状记忆合金马氏体相变的自协调和马氏体中形成的各种界面(孪晶面、相界面、变体界面)的滞弹性迁移，形状记忆合金会吸收能量而具有很好的阻尼特性[12−13]，故记忆合金的力学模型等效为弹簧−阻尼。在已发现的上百种记忆合金材料中，Ti-Ni合金的研究发展十分迅速，其具有很好的稳定性及超弹性，已成为记忆合金领域的一个重要研究方向，本实验系统选用近等原子比Ti-Ni合金作为减振材料。

基于形状记忆合金被动减振的飞轮控制系统的力学模型可简化为如图2所示的单自由度弹簧−阻尼结构。图2中：1为连接架的质量；1和1分别为记忆合金圈的刚度和阻尼；2和2分别为弹簧和记忆合金丝组合结构的刚度和阻尼。飞轮在旋转过程中，由于质量分布不均，会产生离心惯性力，并随着转速的提高而增大。设偏心距为，偏心质量为2，飞轮转动的角速度为，则飞轮转动时产生的离心惯性力为22sin()。

图2 减振实验平台等效数学模型

取1=2=，1=2=，则系统的强迫振动方程为

1d2()/d2+2d()/d+2()=22sin() (1)

对式(1)变形可得

d2()/d2+d()/d+()=sin() (2)

式中：=2/1；=2/1；=22/1。常温下，Ti-Ni形状记忆合金等效阻尼可表示为

=/(π02) (3)

式中：为1个振动周期内记忆合金消耗的能量；0为1个振动周期内记忆合金的振幅[14−15]。

2 基于形状记忆合金被动减振的飞轮控制系统非线性振动研究

2.1 飞轮控制系统被动减振机理

假设连接架的质量1=0.5 kg，飞轮的偏心质量2=0.5 g，偏心距=1 mm，基于形状记忆合金被动减振的轮控制系统转速=10 000 r/min，则基于形状记忆合金被动减振的轮控制系统工作时产生的激励幅值≈1 N。取=1 N，则方程(2)可化为

d2()/d2+4cd()/d+4()=sin() (4)

式中：ω=21/2。受迫振动的频率与激振频率相同。由方程的非奇次项为正弦函数可设稳态响应方程为

()=sin(−) (5)

式中：为基于形状记忆合金被动减振的飞轮控制系统稳态响应振幅；为位移落后于激振力的相位角。

令/2()1/2=λ，2/()1/2=，可求得：

基于形状记忆合金被动减振的飞轮控制系统隔振系数为

由上述结果可知，基于形状记忆合金被动减振的飞轮控制系统振动响应的幅值取决于该系统本身的性质以及激励幅值。随着基于形状记忆合金被动减振的飞轮控制系统转速的提高，激励幅值也逐渐变大。为减小响应幅值，需从调整基于形状记忆合金被动减振的飞轮控制系统刚度及阻尼比的角度考虑。

理论上，只有当＞21/2时基于形状记忆合金被动减振的飞轮控制系统才有减振效果；当＞5时，曲线几乎水平，即使使用更好的减振装置，基于形状记忆合金被动减振的飞轮控制系统的减振效率提高仍然有限[16]；当＞21/2时，基于形状记忆合金被动减振的飞轮控制系统的减振系数随ζ的增大而增大，在此情况下阻尼的增大并不利于减振。由＞21/2可得＞2(2)1/2。为保证基于形状记忆合金被动减振的飞轮控制系统的减振效果，的取值应较小。当>>1或者<<1时，阻尼衰减振幅的作用不大；当≈1时，基于形状记忆合金被动减振的飞轮控制系统的振幅随着阻尼的增加明显减小，此时，阻尼对基于形状记忆合金被动减振的飞轮控制系统共振振幅有明显的抑制作用。因此，在基于形状记忆合金被动减振的飞轮控制系统满足减振条件(＜1)的情况下，应确保阻尼的取值较大。

2.2 飞轮控制系统被动减振动力学仿真分析

采用UG6.0与ADAMS2010对基于形状记忆合金被动减振的控制系统进行动力学仿真，仿真流程如图3所示。

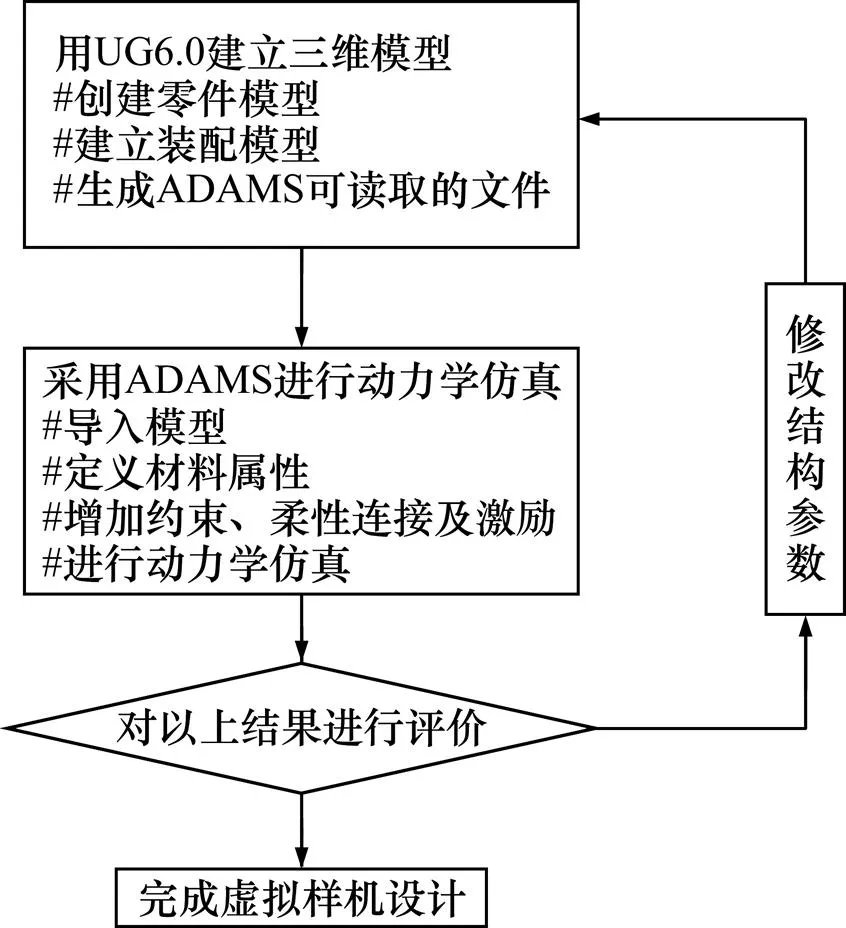
图3 储能调姿飞轮被动减振实验平台动力学仿真流程

2.2.1 飞轮控制系统被动减振动力学模型

记忆合金圈材料为Ti-Ni形状记忆合金，其他部分采用不锈钢材料。其中Ti-Ni合金的泊松比为0.3，弹性模量=80 GPa，密度为6.450 t/m3。该模型共有1个固定副，8个阻尼器，1个激励，若干弹簧及记忆合金丝，如图4所示。

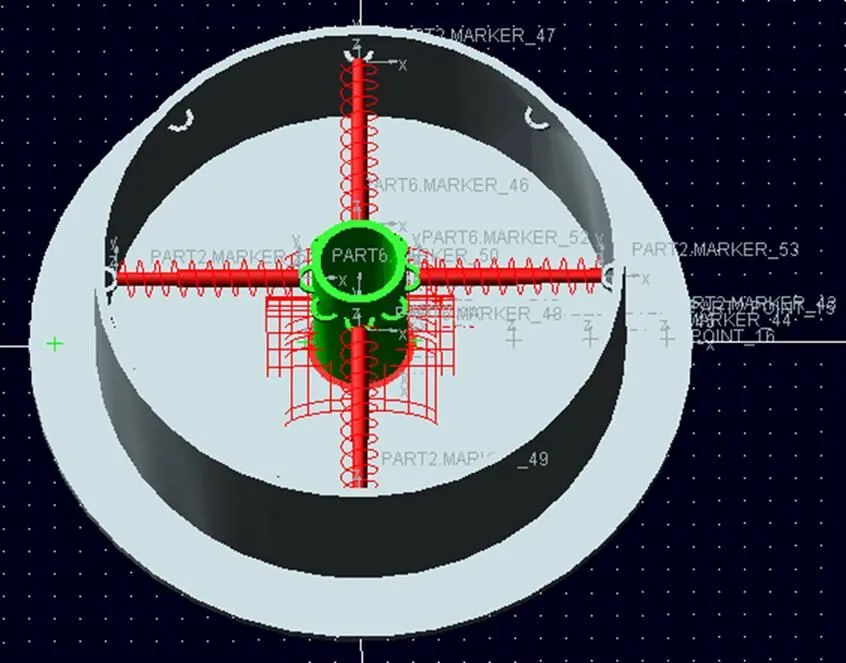
图4 飞轮控制系统被动减振动动力学模型

记忆合金圈与连接架和舱壁之间分别采用阻尼器连接，在飞轮控制系统的飞轮上施加一旋转激励，激励幅值为1，相位为0°。在舱壁上距离飞轮中心60，90和120 mm处取测试点1，2和3，分别测量其在，和方向的振动响应值。

2.2.2 飞轮控制系统被动减振动力学仿真结果

仿真频率设置为0.1~1 000 Hz，当不采取减振措施时，测得飞轮控制系统各点在方向的振动仿真曲线如图5所示。由图5可知：在低频激励的作用下，振动幅值相应较小；在高频激励的作用下，振动幅值相对较大，且振动幅值变化剧烈；距离中心点近的测试点振动幅值比距离中心点远的测试点的振动幅值要大。

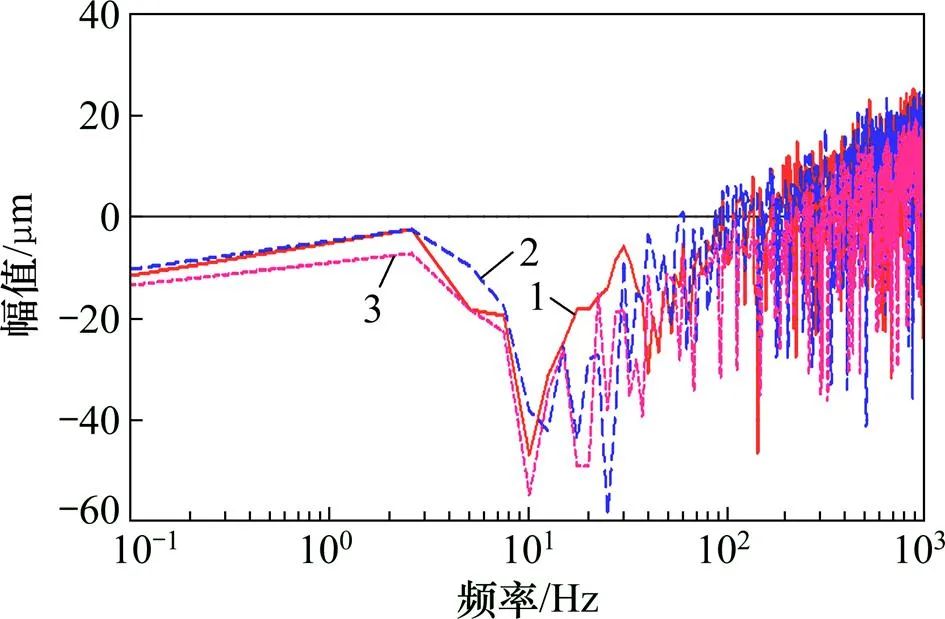
1—测试点1；2—测试点2；3—测试点3

分别在连接架与记忆合金之间以及记忆合金与舱壁之间施加对称分布的4个套筒力，且将记忆合金等效为连接架上部与舱壁之间分别施加的对称分布的4个记忆合金弹簧−阻尼结构或8个记忆合金弹簧−阻尼结构。飞轮控制系统被动减振仿真曲线如图6所示。

(a) 加载4个记忆合金弹簧−阻尼结构；(b) 加载8个记忆合金弹簧−阻尼结构

对于施加对称分布的4个记忆合金弹簧−阻尼结构的飞轮控制系统，在弹簧刚度=10 N/mm，记忆合金弹簧−阻尼结构阻尼=10−3N·s/mm时，减振效果较理想，仿真曲线如图6所示。此时飞轮控制系统的一阶频率为400 Hz，可有效避开飞轮控制系统工作的高频段。当增加记忆合金弹簧−阻尼结构的数为8个时，记忆合金弹簧−阻尼结构的阻尼值明显增加，导致飞轮控制系统的测试点响应最大幅值明显减小，此时飞轮控制系统的一阶固有频率为150 Hz，减振效果要优于加载4个记忆合金弹簧−阻尼结构时的效果。

2.3 飞轮控制系统被动减振实验

基于8个记忆合金弹簧−阻尼结构的被动减振飞轮控制系统实验设备主要包括数据采集系统(型号为LMS SCADAS Mobile)、传感器(型号为356A24)、非减振飞轮控制系统模型、基于记忆合金与8个弹簧阻尼结合的被动减振的飞轮控制系统模型、电机控制器和24 V稳压电源等。其中，飞轮控制系统由直流无刷电机系统来模拟，该电机系统调速方便，可有效模拟飞轮工况。

为方便记录，实验中对非减振飞轮控制系统模型和基于8个记忆合金弹簧−阻尼结构被动减振飞轮控制系统模型的采样点按照距离中心位置33.5，68.5和108.5 mm处3点由近及远的顺序分别标记为1，2和3，在电机激励频率分别为25，50，75，100和125 Hz时，非减振飞轮控制系统模型和被动减振飞轮控制系统模型的采样点1，2和3的振动幅值如图7所示。从图7可以看出：在电机激励频率分别为25，50，75，100和125 Hz时，基于8个记忆合金弹簧−阻尼结构被动减振的飞轮控制系统模型采样点1，2和3的振动幅值均较小，但随着离中心点的距离增加而略微减小。而对于非减振飞轮控制系统模型，采样点1，2和3的振动幅值均较大，且随着频率的增加，采样点1，2和3的振动幅值呈先减小后增加的趋势，而随着离中心点的距离增加，减振飞轮控制系统模型振动幅值减小较多。

采样点：(a) R1；(b) R2；(c) R3

与非减振飞轮控制系统模型相比，在不同频率下，基于8个记忆合金弹簧−阻尼结构的被动减振飞轮控制系统模型的振动幅值要低24.4%~55.2%。可见：基于8个记忆合金弹簧−阻尼结构的被动减振方式对于加大飞轮控制系统模型的阻尼十分有效，并具有较好的减振效果。

为验证非减振飞轮控制系统模型和被动减振飞轮控制系统模型的振动衰减特性，在电机激励频率为100 Hz且匀速运转时突然切断电流，研究非减振飞轮控制系统模型和被动减振飞轮控制系统模型振动衰减对比情况，其振动衰减趋势如图8所示。

(a) 不采取减振措施；(b) 记忆合金与8个弹簧阻尼被动减振

从图8可以看出：当为14 s左右时，基于8个记忆合金弹簧−阻尼结构的被动减振飞轮控制系统模型振动衰减基本上接近于0 mm，而此时非减振飞轮控制系统模型振动衰减还不到40%：因此，基于8个记忆合金弹簧−阻尼结构的被动减振方式可有效加大飞轮控制系统模型的阻尼，可确保飞轮控制系统模型能较快地耗散振动能。

3 结论

1) 采用形状记忆合金被动减振方式构建了飞轮控制系统及其动力学模型。基于形状记忆合金被动减振的飞轮控制系统的振幅随着记忆合金弹簧−阻尼结构阻尼值的增加而明显减小，且减振效果较好。

2) 在不同频率下，基于8个记忆合金弹簧−阻尼结构的被动减振飞轮控制系统模型的振动幅值要比非减振飞轮控制系统模型振动幅值低24.4%~55.2%，并具有较好振动衰减效果。

[1] Masterson R, Miller D, Grogan R. Development and validation of reaction wheel disturbance models: Empirical model[J]. AIAA Journal of Sound and Vibration, 2002, 249(3): 575−598.

[2] Wei F, Zheng G T. Nonlinear vibration analysis of space-craft with local nonlinearity[J]. Mechanical Systems and Signal Processing, 2010, 24(2): 481−490.

[3] Pulecchi T, Casella F, Lovera M. Object-oriented modeling for spacecraft dynamics: Tools and applications[J]. Simulation Modelling Practice and Theory, 2010, 18(1): 63−86.

[4] 王全武, 虎刚. 飞轮扰动原因与测量技术现状[J]. 空间科学学报, 2009, 29(1): 39−44.
WANG Quanwu, HU Gang. Analysis of flywheel disturbance and measuring technology[J]. China Journal of Space Science, 2009, 29(1): 39−44.

[5] 孙贤军, 王树文, 张天序. 反作用轮干扰对三轴稳定地球同步卫星姿态影响分析[J]. 计算机与数字工程, 2005, 33(12): 55−59.
SUN Xianjun, WANG Shuwen, ZHANG Tianxu. Effects of reaction wheel induced disturbance on the attitude of three axis stabilized geostationary satellite[J]. Computer & Digital Engineering, 2005, 33(12): 55−59.

[6] Gregory W N, James W M, Boris J L. Vibration attenuation approach for space borne optical interferometers[J]. IEEE Transactions on Control Systems Technology, 1998, 6(6): 689−700.

[7] E Jiaqiang, QIAN Cheng, LIU Teng, et al. Research on the vibration characteristics of the new type of passive super static vibratory platform based on the Multi-objective parameter optimization[J]. Advances in Mechanical Engineering, 2014, 2014: 1−8.

[8] Peng Z K, Meng G, Lang Z Q, et al. Study of the effects of cubic nonlinear damping on vibration isolations using Harmonic balance method[J]. International Journal of Non-Linear Mechanics, 2012, 47(10): 1073−1080.

[9] Megahed S M, Abd El-Razik A K H. Vibration control of two degrees of freedom system using variable inertia vibration absorbers:Modeling and simulation[J]. Journal of Sound and Vibration, 2010, 329(23): 4841−4865.

[10] Manjaiah M, Narendranath S, Basavarajappa S. Review on non-conventional machining of shape memory alloys[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(1): 12−21.

[11] Masuda A, Noorib M. Optimization of hysteretic characteristics of damping devices based on pseudoelastic shape memory alloys[J]. International Journal of Non-linear Mechanics, 2002, 37(8): 1375−1386.

[12] Belyaev S Y, Volkov A, Resnina N. Alternate stresses and temperature variation as factors of influence of ultrasonic vibration on mechanical and functional properties of shape memory alloys[J]. Ultrasonics, 2014, 54(1): 84−89.

[13] Zakerzadeh M R, Sayyaadi H. Precise position control of shape memory alloy actuator using inverse hysteresis model and model reference adaptive control system[J]. Mechatronics, 2013, 23(8): 1150−1162.

[14] JIANG Shuyong, ZHAO Yanan, ZHANG Yanqiu, et al. Effect of solution treatment and aging on microstructural evolution and mechanical behavior of NiTi shape memory alloy[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(12): 3658−3667.

[15] Seelecke S. Modeling the dynamic behavior of shape memory alloys[J]. International Journal of Non-linear Mechanics, 2002, 37(8): 1363−1374.

[16] 于德介, 程军圣, 杨宇. 机械振动学[M]. 长沙: 湖南大学出版社, 2010: 25−48.
YU Dejie, CHENG Junsheng, YANG Yu. Mechanical vibration[M]. Changsha: Hunan University Press, 2010: 25−48.

Nonlinear vibration analysis on flywheel control system of passive damping based on SMA

E Jiaqiang1, 2, WANG Jingyang2, QIAN Cheng2, WANG Shuhui1, 2, LIU Teng2, CAI Hao1, 2

(1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University, Changsha 410082, China;2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China)

In order to reduce the influence of the vibration which appears when the flywheel control system works, the flywheel control system and its dynamic model with shape memory alloy were built in passive vibration damping way, and passive vibration damping mechanism and simulation on flywheel control system were analyzed. The results show that the vibration amplitude of flywheel control system with shape memory alloy in passive vibration damping way obviously reduces with the increase of the damping value of shape memory alloy spring-damping structure. With the increase of different frequencies, the vibration amplitude of flywheel control system model based on shape memory alloy spring-damping structure in passive vibration damping way is obviously lower than that of non-damping flywheel control system model and is of better vibration damping effect.

flywheel control system; passive vibration damping; shape memory alloy; nonlinear analysis; vibration

TJ861

A

1672−7207(2015)02−0519−06

2014−02−12；

2014−04−22

武器装备预研重点基金项目(9140A2011QT4801)(Project (9140A2011QT4801) supported by Weapons and Equipment Pre-research Fund)

鄂加强，博士，博士生导师，从事智能监测与智能控制技术研究；E-mail：ejiaqiang@126.com

10.11817/j.issn.1672-7207.2015.02.021

(编辑 陈灿华)