电动轮自卸车发动机扭转振动分析与试验研究

张伟，杨珏，张文明，赵翾，郭苗苗



电动轮自卸车发动机扭转振动分析与试验研究

张伟1，杨珏1，张文明1，赵翾1，郭苗苗2

(1. 北京科技大学 机械工程学院，北京，100083；2. 北汽福田汽车工程研究院，北京，102206)

针对电动轮自卸车发动机和发电机系统轴系扭转振动问题进行分析，并通过试验进行验证，提出分析此类轴系扭转振动的研究方法。根据电动轮自卸车的动力传递系统由发动机和发电机直接刚性连接而成的特点，对系统轴系进行固有振动特性和强迫振动特性分析时，建立轴系扭转振动分析的集总质量参数模型，利用系统矩阵法和能量法获得轴系的固有频率和振型。在试验验证阶段，采用非接触式扭转振动测量法进行试验验证，对比分析计算结果和试验验证结果。研究结果表明：分析计算和试验验证基本吻合，证明了针对此类轴系扭转振动分析计算方法的可靠性，并获得轴系扭转振动发生共振的主谐次和强谐次，为进一步进行扭转振动减振分析及部件设计提供了依据。

电动轮自卸车；发动机；发电机；轴系；扭转振动；数学模型

电动轮自卸车采用发动机和发电机直接串联模式代替了原有的传动轴、变速器、差速器及减速器等，车辆结构大大简化。发动机与发电机直接刚性连接，由二者组成的轴系与传统机械传动差别较大，属于多振动类型的复杂振动系统。轴系的扭转振动不仅受到机械方面的影响，而且受到电磁方面的影响，轴系的激振力类型发生显著变化。电动轮自卸车工作的矿山频繁出现上坡、下坡的山区路面，车辆空载和满载交替运行，因此，发电机转速变化频率较高、磁场变化显著，轴系扭转振动随之变化。扭转振动分析对保证动力总成的工作可靠性、降低轴系的振动和噪声有显著影响[1]。发动机扭转振动分析一直是国内外学者研究的重点。文献[2]通过简化轴系模型，采用振动理论计算求取自由振动和强迫振动的相关特性；文献[3]采用多体系统仿真的方法建立轴系的三维模型进行仿真计算分析；文献[4]通过采用试验测量的方法研究相关附件对轴系扭振的影响。本文作者结合电动轮自卸车的工作特点，采用系统矩阵法和能量法分别对轴系进行固有特性和强迫振动分析，同时采用非接触式扭转振动测量法进行试验验证，对比分析计算结果和试验结果，验证求解分析的可靠性与准确性。

1 试验测试系统

电动轮自卸车的发电机直接与发动机相连，其发出的电通过整流器和逆变器之后直接供给轮边电动机，从而驱动车辆前进。动力传递系统主要包括发动机、发电机、整流器、逆变器、轮边电机等。电动轮自卸车动力传递结构示意图如图1所示。

图1 电动轮自卸车动力传递结构示意图

1.1 试验测量方法

图2所示为试验测试所用的扭振测量装置示意图。试验中采用非接触式扭振测量法，测量装置不直接安装在轴系上，利用发动机飞轮和轴系自由端齿轮，通过磁电传感器采集信号，利用LMS-QTV转换拾取扭振信号。该种测量方法的测量精度高，使用方法简便，反应速度快，而且试验测试系统本身对轴系扭转振动没有影响[4]。

图2 扭转振动测量装置示意图

1.2 试验用发动机和发电机相关参数

试验用发动机选用Cummins QSL9-325柴油发动机，其额定功率为242 kW，额定转速为2 100 r/min，气缸数为6，气缸直径为0.114 m，冲程系数为2，曲柄半径为201 mm。

选取兰州电机有限责任公司的TFBPW-355-8型无刷同步发电机，其额定功率为230 kW，额定频率为120 Hz，额定转速为1 800 r/min，额定电压为660 V，额定电流为201 A。

2 轴系固有频率和固有振型

2.1 系统的当量转化

采用集总质量模型简化得到当量系统是九质量、八自由度的当量系统，如图3所示，其中，1为风扇驱动的转动惯量；27为发动机6个活塞连杆的转动惯量；8为发动机飞轮的转动惯量；9为发电机转子转动惯量；1,2为风扇连接装置刚度；2,3~7,8为相邻两曲拐之间的主轴颈刚度；8,9为发电机转子轴刚度。发动机和发电机系统轴系多质量系统当量转化各参数示意图如图3所示。

图3 多质量系统各参数示意图

2.2 系统固有频率和固有振型

多质量系统的自由扭转振动计算，目前常用的方法有霍尔茨(Holzer)表格法、系统矩阵法(应用行列式展开求根方法或迭代法)、传递矩阵法(或称迁移矩阵法)等方法[5]，其中系统矩阵法可以归结为求矩阵方程的特征值和特征根的问题，计算简便，本文采用计算机辅助计算的系统矩阵法。

多质量系统的扭转振动的动力学方程为

其中：

利用MATLAB编程，直接求得系统的特征根和特征向量，即可得到多质量系统的固有频率和振型，如表1和图4所示。

表1 轴系的固有频率

1—一阶；2—二阶；3—三阶；4—四阶；5—五阶；6—六阶；7—七阶

从图4可以看出：发动机−发电机轴系第一阶振型几乎没有波动；第二、三阶振型轴系波动较明显；从第四、五、六、七阶振型中可以看到轴系波动均比较剧烈，但这几阶的频率较高(均大于3 000 rad/s)，一般不容易发生共振，因此，在后面的讨论中以前3阶振型为主要研究振型。

3 激振力矩

激励力矩是引起系统扭转振动的能量来源，是研究扭转振动必不可少的环节，激励力矩的振幅和频率往往影响到相应的响应的振幅和频率[6]。主要干扰力矩包括发动机气缸内气体压力变化产生的作用力矩、发动机活塞曲柄连杆机构往复运动产生的惯性力矩和发电机的电磁激励等[7]。

作用于单个曲拐上的转矩为

其中：g为缸内气体作用力；j为往复惯性力。该函数为周期函数，四冲程发动机。

3.1 缸内气压产生力矩的简谐分析

将函数进行傅里叶级数展开可得：

其中：为曲轴运转周期，=4π/；为曲轴的角速度；M为次谐力矩的幅值；k为其初相角；0为基频；M为平均转矩，只引起曲轴的静扭转变形，不引起激振作用，故轴系所受到的缸内气压产生力矩g由式(3)写为

3.2 往复惯性力产生力矩

发动机曲柄连杆机构的惯性力包括离心惯性力和往复惯性力2种，离心惯性力的作用线通过曲轴的回转中心，故对曲轴的作用力矩为0，不产生扭转振动。而往复惯性力作用在活塞销的中心，通过连杆传到连杆轴颈，对曲轴产生周期性变化的切向力矩M，该力矩也是引起轴系扭转振动的动力[8−9]，其计算求解公式为

其中：j为往复运动部件的质量。j仅包含整数次谐量，次数越高，谐量的幅值越小，一般取到4次。

3.3 电磁转矩

系统电磁转矩为[10]

其中：为电机转子转角；为电机气隙磁场能。

3.4 系统定轴转动的动力学方程

发动机和发电机系统定轴转动的动力学方程为

其中：0为轴系的转动惯量。

4 强迫振动分析

4.1 共振转速和强共振节次的确定

当激振力矩的次谐波圆频率ω与轴系的某阶固有频率f相等时，轴系发生共振[11]。

自由振动的周期数N为

共振时，曲轴转速为c，角速度为c，则

4.2 共振振幅计算

目前常用的共振振幅计算方法有系统矩阵法、能量法和动力放大系数法。这里选用能量法计算[12]。强迫振动中系统激振力矩所做的功Q等于阻尼力消耗的功c，即

激振力矩所做的功为

阻尼力所做的功为

其中：c为曲柄连杆机构当量质量上作用的黏性外阻尼，此时轴系简化模型示意图如图5所示。

图5 轴系的简化模型

根据式(14)，第1质量振幅为

4.3 振型求解

根据车辆发动机动力学理论，发动机的简谐干扰力矩是(=3，5，7，9，…)的谐量， 简谐力矩矢量在同一条直线上，并且方向相同，一旦这些谐量的干扰力矩引起共振，振动往往占主要作用，因此，这些谐次的干扰力矩为发动机的主简谐；简谐干扰力矩是(ν=1.5，4.5，…)的谐量，虽然简谐矢量也在1条直线上，但一、二、三缸的方向向上；四、五、六缸的方向向下；它们对轴系的作用也比较强烈，为发动机的强简谐[13]。在发动机扭振计算中，一般对主简谐、强简谐引起的共振都要进行计算，因为这是最危险的情况。

发动机激励谐波和固有频率关系图如图6所示。从图6可以看到，轴系一阶自然频率落在了发动机激励的第1.5和2.0谐波的频率范围内；二阶自然频率落在了第5.0，5.5，6.0，6.5，7.0和7.5谐波的频率范围内；三阶自然频率落在了第12谐波的频率范围内，横坐标为引起共振的发动机临界转速。

图6 发动机的激励谐波和固有频率关系

本文所研究的发动机是直列六缸柴油发动机，常用转速范围为1 300~2 100 r/min，运转角速度范围为136.14~219.91 rad/s。采用相似理论[14]，求出各次简谐力矩振幅和相位。根据简谐系数通用曲线及式(18)可求得所需简谐力矩的振幅，取值如表2所示。

表2 简谐力矩的扭矩振幅

由表2和图6可知：所要研究的对轴系干扰比较强烈的主简谐、强简谐，这些简谐波引起共振时的共振频率和发动机临界转速如表3所示。

表3 对轴系干扰比较强烈的谐次

5 试验结果对比分析

根据前述分析可知，发动机与发电机组成的轴系可能激起危险共振的干扰力矩谐次[15]。在全负荷运转状态下对发动机和发电机组成的轴系扭转振动振幅的实验测试。图7所示为脉冲信号和相对扭角信号输出曲线。各谐次的扭转振幅及各谐次的转速相对扭转振幅如图8~11所示。

(a) 转速脉冲信号；(b) 相对扭角信号

从图8可以看出：最大扭转振幅出现在1.5谐次，此时发动机转速为1 942 r/min，对应的频率为45.55 Hz；同时，系统在低速全负荷运转时1谐次、2 谐次扭转振动的振幅也较大，但不是曲轴本身的固有频率，由前面分析可知均为激励干扰比较强烈的谐次所导致。所以，自卸车在此转速段工作时，尽量避免全负荷工作，这与实际工况也是相符合的。

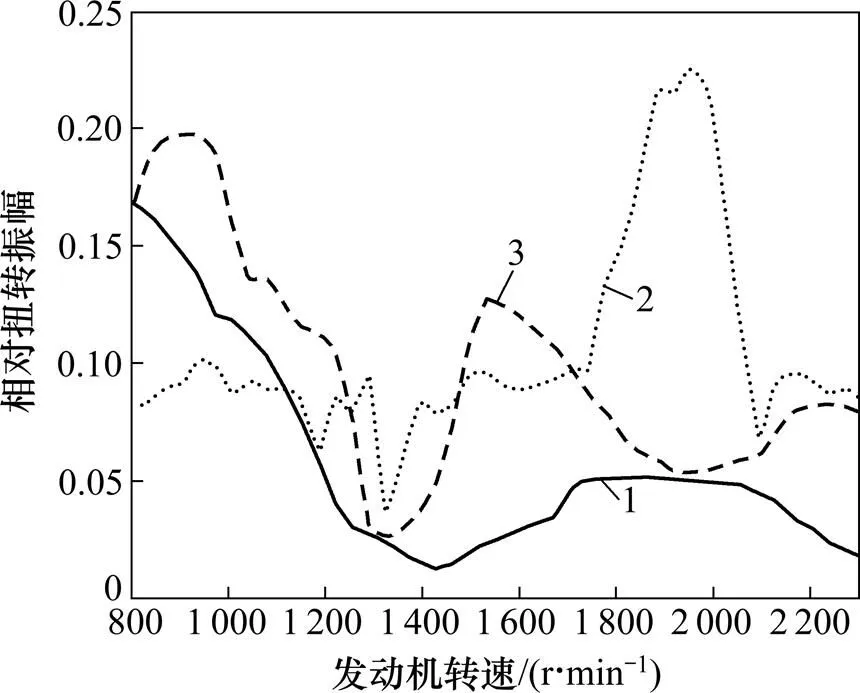
谐次：1—1；2—1.5；3—2

从图9可以看出：扭转振动6谐次时，发动机在1 716 r/min时出现波峰，对应的频率为171.6 Hz；扭转振动12谐次时，发动机在2 065 r/min时出现波峰，对应的频率为413 Hz。6和12谐次出现共振现象，但是扭振幅值均在允许的范围之内。

谐次：1—4；2—6；3—8；4—12

从图10可知：各个强谐次扭转振幅在整个转速范围内变化比较平缓且很小，扭转振动3谐次时发动机在1 325 r/min时出现波峰，但相对振幅在0.03以下，其他谐次振幅也都很小。

人力资本理论起源于经济学研究，17世纪经济学家威廉·配第首次提出劳动决定价值基本理论，之后亚当·斯密、马歇尔、费雪等人对其进行了补充和完善。人力资本理论的构建者美国经济学家西奥多·W·舒尔茨认为，人力资本是凝结在人身上的资本，包括教育、职业培训支出以及机会成本，是以人为载体的各种知识技能存量的总和；人力资本是最重要的资源，其促进国民收入增加的作用优于其他物质资本；应当把人力资本看作是一种投资而非消费行为，教育投资是提升人力资本的主要手段［1］。

谐次：1—3；2—5；3—7；4—9

从图11可知：各个谐次的扭转振幅都比较小，虽然也会出现波峰值，但是相对扭转振幅均小于0.006，其他转速下更小。

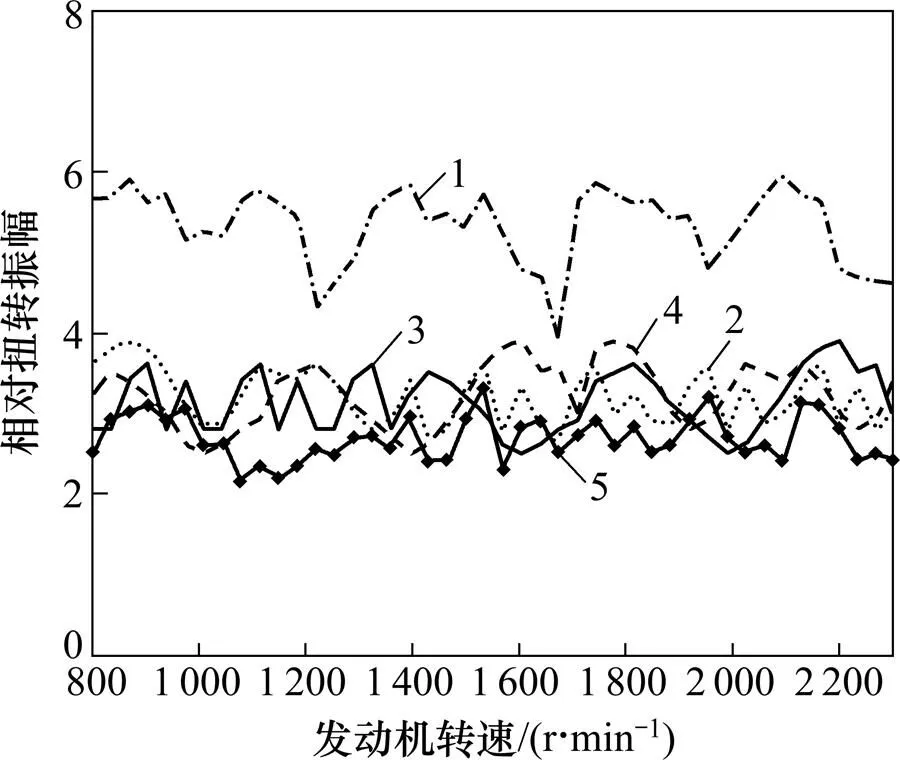
谐次：1—3.5；2—4.5；3—5.5；4—6.5；5—7.5

根据以上实验数据结果分析可以发现：电动轮自卸车的发动机和发电机系统组成的轴系，干扰激励在1.5，6.0和12.0谐次出现共振现象，扭转振动振幅出现波峰，但是幅值不大，未超过允许范围，不会危害到轴系的安全性。最大扭转振幅出现在1.5谐次，其他谐次较小，与计算结果相符。

6 结论

1) 在扭转振动分析中，将电动轮自卸车发动机和发电机组成的复杂轴系系统转化为若干用惯量轴段互相连接起来的集总质量参数系统，采用系统矩阵法对轴系固有振动进行分析，采用能量法对激励干扰振动进行求解，试验测试采用精度较高的非接触式扭转振动测量法，保证了理论分析和试验验证的可靠性。

2) 轴系扭转振动固有频率比较高，一阶、二阶和三阶出现在工作转速范围内，出现扭转振动振幅波峰的简谐干扰激励谐次为1.5，6.0和12.0，其中1.5次振幅最大，其他谐次较小，但均在允许的范围之内，因此，在实际工作中，应避免车辆长时间运行在临界转速附件。

3) 在轴系扭转振动计算中，综合考虑发动机的激励力矩和发电机的电磁激励，同时将风扇驱动装置进行了当量质量模型化，试验测试中考虑系统在满载情况下运转，这些使得分析更符合实际工作情况。通过对比发现试验结果与理论分析结果基本一致，证明了计算分析方法的可靠性，为此类车辆轴系扭转振动减振、部件设计及深入研究提供理论依据和可靠的分析计算方法。

[1] Saravanan K, Sekhar A S. Crack identification in a cantilever beam using rotational laser vibrometer-based coupled of bending, axial and torsional vibrations[J]. International Journal of Structural Engineering, 2012, 3(4): 267−282.

[2] Collina A, Prone L, Ruspini E, et al. Study of torsional vibrations in the powertrain of diesel locomotive during maneuvering by means of a multi-body model[J]. International Journal of Heavy Vehicle Systems, 2013, 20(2): 120−143.

[3] Henao H, Kia S H, Capolino G A. Torsional-vibration assessment and gear-fault diagnosis in railway traction system[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1707−1717.

[4] Charles P, Sinha J K, Gu F, et al. Detecting the crankshaft torsional vibration of diesel engines for combustion related diagnosis[J]. Journal of Sound and Vibration, 2009, 321(3): 1171−1185.

[5] Ishihara T, Emori R I. Torque converter as a vibration damper and its transient characteristics[J]. Measurement, 2013(12): 4−12.

[6] Karabulut H. Dynamic model of a two-cylinder four-stroke internal combustion engine and vibration treatment[J]. International Journal of Engine Research, 2012, 13(6): 616−627.

[7] Keskin A. The influence of ethanol-gasoline blends on spark ignition engine vibration characteristics and noise emissions[J]. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2010, 32(20): 1851−1860.

[8] Guo Z, Yuan C, Liu P. Study on identification model of cylinder liner-piston ring using vibration analysis based on fuzzy C-means clustering[J]. Open Mechanical Engineering Journal, 2012, 6(2): 126−132.

[9] Kishore P, Dinakar D, Shankar M S, et al. Non-contact vibration sensor using bifurcated bundle fiber for real time monitoring of diesel engine[J]. International Journal of Optoelectronic Engineering, 2012, 2(1): 4−9.

[10] Villa L F, Reñones A, Perán J R, et al. Statistical fault diagnosis based on vibration analysis for gear test-bench under non-stationary conditions of speed and load[J]. Mechanical Systems and Signal Processing, 2012, 29(11): 436−446.

[11] 舒歌群，谭琳琳，卫海桥，等. 基于发动机轴系扭振抑制的扭弯减振器分析[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(11): 951−957.
SHU Gequn, TAN Linlin, WEI Haiqiao, et al. Analysis on torsional-bending damper for engine crankshaft based on torsional vibration reduction[J].Journal of Tianjin University (Science and Technology), 2013, 46(11): 951−957.

[12] Periyasamy S, Alwarsamy T. Combined effects of inertia and pressure on engine vibration[J]. Journal of Vibration and Control, 2013, 19(16): 2469−2480.

[13] Zheng G, Ohta K. Investigation of piston slap induced vibration of IC engine considering the coupled vibration of connecting rod, crankshaft and engine block[J]. International Journal of Powertrains, 2014, 3(1): 75−89.

[14] Kang J H. Three-dimensional vibration analysis of joined thick conical−cylindrical shells of revolution with variable thickness[J]. Journal of Sound and Vibration, 2012, 331(18): 4187−4198.

[15] 李晓茜, 王刚, 吕秉琳, 等. 短路工况下柴油发电机组轴系扭振计算方法及特性研究[J]. 内燃机工程, 2013, 34(2): 18−23.
LI Xiaoqian, WANG Gang, LÜ Binglin, et al. Calculation method and characteristics analysis of torsional vibration of diesel generating set shaft system in short circuit condition[J]. Chinese Internal Combustion Engine Engineering, 2013, 34(2): 18−23.

Dynamic characteristics and test analysis of torsional vibration of diesel engine at motor dump truck

ZHANG Wei1, YANG Jue1, ZHANG Wenming1, ZHAO Xuan1, GUO Miaomiao2

(1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;2. Automotive Engineering Research Institute, Beiqi Foton Motor Co., Ltd., Beijing 102206, China)

To solve the problem of torsional vibration of the engine and generator shafting in motor dump truck, through mathematical modeling analysis and experimental verification, a method was provided to analyze the torsional vibration. The powertrain system includes engine, generator and directly rigid connection between them. According to the structure, a lumped mass shaft system model was established for calculating the characteristics of free vibration and forced vibration. And the system natural frequencies and vibration modes were obtained with the matrix method and energy method though the model. Meanwhile, non-contact measurement was used in the torsional vibration test. The calculation results were compared with the test results. The results show that the calculation results and the test results are coincident, which proves that the calculation method is reliable for studying the torsional vibration in this type shafting, and the main and powerful order harmonic are obtained when shafting torsional vibration has resonance. So, the results provide a theoretical basis and method for truck design and further study in torsional vibration reduction.

motor dump truck; engine; generator; shafting; torsional vibration; mathematical model

U270.1；TK423.3

A

1672−7207(2015)02−0512−07

2014−04−10；

2014−07−08

国家高技术研究发展计划(863计划)项目(2011AA060404)；中央高校基本科研业务费资助项目(FRF-MP-13-007A) (Project (2011AA060404) supported by the National High Technology Research and Development Program of China (863 Program); Project (FRF-MP-13-007A) supported by the Fundamental Research Funds for the Central Universities)

张伟，博士研究生，从事电动轮车辆发动机扭转振动研究；E-mail：zlg1314@yeah.net

10.11817/j.issn.1672-7207.2015.02.020

(编辑 赵俊)