随机路面激励下汽车悬架弹簧应力分析

陈双，梁金刚（.辽宁工业大学汽车与交通工程学院，辽宁 锦州 00；.辽沈工业集团驻七二四厂，辽宁 沈阳 0045）

随机路面激励下汽车悬架弹簧应力分析

陈双1，梁金刚2
（1.辽宁工业大学汽车与交通工程学院，辽宁 锦州 121001；2.辽沈工业集团驻七二四厂，辽宁 沈阳 110045）

基于整车八自由度动力学模型和路面四轮相关随机输入时域模型，得到了悬架弹簧随机应力的时间历程，在此基础上采用离散二进小波变换，对弹簧随机应力时间历程进行多层小波分解及重构，并对分解后的应力历程应用改进的四峰-谷值雨流计数法进行统计分析，得到应力频次的分布情况。研究结果为汽车悬架零件的疲劳损伤分析提供新的参考。

汽车；悬架弹簧；随机应力；小波分析；雨流计数

10.16638/j.cnki.1671-7988.2015.12.019

CLC NO.: U463.3Document Code: AArticle ID:1671-7988(2015)12-53-05

引言

随着汽车工业和交通运输业的快速发展，汽车运行的安全性和可靠性已引起相关部门的高度重视，因此对汽车承载构件进行可靠性疲劳设计和寿命分析是十分必要的。目前疲劳分析方法有时域法和频域法。时域法是应用峰值计数法、穿越计数法、雨流计数法等对实测构件的随机应力进行循环计数，编制随机载荷谱，对构件进行疲劳寿命研究。这种方法试验工况要考虑车辆载荷、行驶速度以及路面条件，因此周期长、费用高[1]。近几年，应用功率谱密度的频域方法发展很快，但对于宽带随机疲劳问题还没有统一的方法[2-3]。

本文基于车辆动力学理论，将小波分析和雨流计数法相结合，利用路面随机激励模型和车辆模型，得到悬架振动系统构件随机振动时域响应，应用小波分析方法对应力时间历程进行统计分析，获得不同频段下应力频次的分布情况，然后利用雨流计数法对各频段应力分布进行统计分析。

1、整车振动系统模型

车辆是一个复杂的振动系统，要建立一个完整的模型全面反映汽车的振动特性是比较困难的，因此，需要具体研究问题对振动系统进行适当的简化。要反映四轮随机输入下整车振动特性（座椅、车身垂直、车身俯仰、车身侧倾、车桥）至少要建立八个自由度(DOF)模型，如图 1所示。八个自由度分别为Zs为座椅垂直位移；Zb为车身质心处垂直位移；Zp为车身仰俯角位移；Zr为车身侧倾角位移；Zfl,Zrl,Zfr,Zrr分别为四个车轮（非簧载质量）的垂直位移。

图1　八自由度整车振动模型

对图1 的力学模型，用拉格朗日方程推导出系统的动力学方程为：[M]z..(t)+[C]z.(t)+[K]z(t)=[Q]q(t)（1）

2、四轮相关路面随机输入时域模型

车辆四轮随机输入模型要考虑前后车轮之间以及左右车轮之间的相关问题[4]。单轮路面随机输入 q1(t)（左前轮）可看成白噪声的一阶滤波输出。右轮路面输入q2(t)根据左右轮的相干函数，并采用二阶Pade近似计算得到左右轮的传递函数，再转换成 q1(t)和 q2(t)的状态方程。左后轮路面输入q3(t)=q1(t-τ)，右后轮的路面输入q4(t)=q2(t-τ)，再写成状态方程。

综合以上过程，可得如下四轮相关路面输入状态方程组

式中

式（3）即为四轮相关路面随机输入的状态方程，当已知路面不平度系数Sq(n0)、路面空间截止频率n00=0.01(1/m)、车速v、轮距B、轴距L参数，可以方便地求出四轮相关的路面随机输入。

3、小波分析方法

设时域信号f(t)，则其连续小波变换为：

f(t)的小波逆变换为：

工程实际中一般是经过实际采样得到离散信号，因此多采用离散小波变换形式。离散小波变换是将式（4）、（5）中a、b离散为 2-j、2-k的形式。即得到离散二进小波变换和逆变换的表达式为：

4、改进的四峰-谷值雨流计数法

雨流计数法简称雨流法，又可称为“塔顶法”，是由英国的Mat-suiski和Endo两位工程师提出的一种计数方法。计数原理如图2所示。计数规则为[6]：

（1）雨流在试验记录的起点和依此在每一个峰值的内边开始，亦即从1,2,3…等尖点开始。

（2）雨流在流到峰值处（即屋檐）竖直下滴，一直流到对面有一个比开始时最大值（或最小值）更正的最大值（或更负的最小值）为止。

图2　雨流计数法原理图

（3）当雨流遇到来自上面屋顶流下的雨时，就停止流动，并构成了一个循环。

（4）根据雨滴流动的起点和终点，画出各个循环，将所有循环逐一取出来，并记录其峰谷值。

（5）每一个雨流的长度可作为该循环的幅值。在判断循环时，通常有两种判别表达式，第一种为：XI≤XI+2且XI+1≤XI+3；第二种为：XI≥XI +2且XI+1≥XI +3，如图3所示：

图3　循环判别模型

对于一般的应力-时间历程，由于雨流法进行完计数后，不能对剩下的发散数据再进行计数，因此常使用全封闭式计数模型来修正原始数据。如图4所示：

图4　全封闭计数模型

在实际计数过程中，一般都采用四峰-谷值雨流计数法进行计数，但其也有一定的局限性。本文将采用一种改进的四峰-谷值雨流计数法，基本思路是：首先，判断峰谷总数的奇偶性，若为偶数，则去掉最后一个波峰（波谷），使载荷时间历程的首尾都是谷值（或都为峰值），并且使首尾都等于它们之中的最低谷值（或最高峰值）。这种改进对原载荷时间历程效果的影响可以忽略不计，因为对于一个较长的纪录样本，最后几个峰谷值对取舍无关紧要，更何况绝大多数的实测时间历程其开始和结尾部分数值都较小而且接近，所以上述改进的影响可以不计。然后，将载荷时间历程从最高处截断，首尾相接重新组成一个以最高峰开始且以最高峰结束的新历程。最后，按照四峰-谷值雨流计数法，反复寻找如图3所示的波形，将符合循环和半循环计数条件的应力取出计算，其基本计数条件写成数学式为：

计算完成后删除所使用的波峰、波谷点，这样不会影响后续计算。在程序中定义变量记录跟踪载荷的波峰和波谷，并用变量记录最大峰值和谷值。

5、汽车悬架弹簧随机应力分析

5.1悬架弹簧应力时间历程

以 C级路面为例，路面不平度系数取为Sq(n0)= 256×10-6m3，v=100km/h。基于 Matlab软件得到的汽车悬架动挠度、动应力时间历程如图5和图6所示：

图5　悬架动挠度时间历程

图6　悬架动应力时间历程

5.2应力时间历程的小波分析

应用Matlab中的Wavelet内置序列的小波包分解与分解系数重构相对应的函数及其算法，编程实现对悬架弹簧应力时间历程的小波分析。小波函数采用Daubechies紧支小波，信号的截断频率为100Hz。对载荷时间历程进行五级小波分解，将信号分解到五个频带：0-3.125Hz，3.125-6.25Hz，6.25-12.5Hz，12.5-25Hz，25-50 Hz。图7和图8分别为C级路面下和B级路面下悬架弹簧应力时间历程小波分解图。图中第一个图形为整车振动下悬架弹簧应力时间历程的原始图，d2-d5表示为疲劳载荷时间历程第二级到第五级小波分解的细节分量图，a5表示为第五级小波分解的近似分量图。从图中可以看出悬架弹簧的应力峰值主要分布在五级小波的低通段即0-3.125Hz频段上。

图7　C级路面应力时间历程各级小波分解图

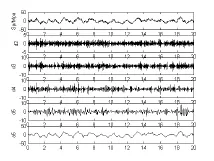
图8　B级路面应力时间历程各级小波分解图

从图中可以看出，S1～S5分频率的描述分析了弹簧应力随时间的变化情况。从图中可以看出，二级小波 12.5～25Hz频段上应力幅值较小，在三级小波 6.25～12.5Hz上，个别应力幅值有所增加，而五级小波0～3.125 Hz频段上应力幅值最大，表明整车振动下悬架弹簧应力峰值主要集中在 0～3.125 Hz频段上，即在此频段上悬架弹簧的疲劳损伤最大。

5.3应力时间历程的雨流统计分析

为了验证小波分析结果，进一步将小波分析前后结果进行对比分析。采用雨流计数法对载荷时间历程进行循环计数，计数规则如图9所示。

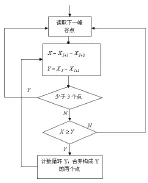
图9　悬架应力载荷循环数提取计数规则

经过雨流计数法后，将每个循环的峰值进行整理，本文将全部峰值分为10组，得到C级路面载荷时间里历程小波分解前和小波分解后峰值分布的统计结果如表1所示。

表1　C级路面应力峰值统计表

表 1中 0-100Hz表示为小波分解前频率，0-3.125Hz、3.125-6.25Hz、6.25-12.5Hz、12.5-25Hz、25-50Hz分别为小波分解后五个不同的频段。从统计结果可以看出，频率在0-3.125Hz范围内的应力分布规律与原始信号的分布规律相近，而频率在 3.125-50Hz范围内的应力幅值全部集中在-10-10MPa范围内，幅值较小，对悬架弹簧的疲劳损伤影响也不大。

表1对应的应力峰值频次直方图如图10、图11所示，图10为C级路面下悬架弹簧小波分解前应力时间历程应力峰值分布图，图11则表示了C级路面下悬架弹簧小波分解后0-3.125频段下悬架弹簧的应力峰值分布图。

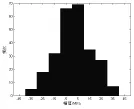
图10　C级路面下小波分解前应力峰值分布

图11　C级路面下小波分解后应力峰值分布（0-3.125HZ）

同理可以得到 B级路面应力峰值频次直方图，如图 12 和13所示，图12为B级路面下悬架弹簧小波分解前应力时间历程应力峰值分布图，图13则表示了B级路面下悬架弹簧小波分解后0～3.125频段下悬架弹簧的应力峰值分布图。

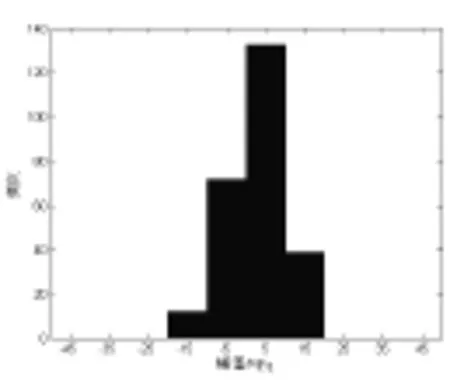
图12　B级路面下小波分解前应力峰值分布

图13　B级路面下小波分解后应力峰值分布（0-3.125HZ）

从图10-图13可以看出，0-3.125Hz的应力峰值分布接近于瑞利分布，与小波分解前原始应力峰值分布一致，反映出悬架弹簧在随机载荷下的峰值分布情况，进一步表明了悬架弹簧在0-3.125HZ频段下最容易产生疲劳损伤。

6、结论

本文采用小波分析技术和雨流计数法对整车振动下的悬架弹簧应力时间历程进行分解，并对分解后的各级小波进行统计，得到悬架弹簧不同频段下的应力分布满足正态分布，为下一步疲劳寿命预测中的疲劳累积损伤理论提供了一定的理论依据。

[1] 姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2003.

[2] 袁毅.基于应力功率谱的结构振动疲劳寿命预测方法研究[D].湖南大学,2014.

[3] 王文涛,上官文斌,段小成,姚斌辉.基于线性疲劳累计损伤橡胶悬置疲劳寿命预测研究[J].机械工程学报,2012(10):56-65.

[4] 张立军,何辉.车辆随机振动[M].沈阳:东北大学出版社,2007.

[5] 王国林,胡蛟,钱金戈,王一琪.路面对汽车非平稳激励的时域仿真及小波分析[J].振动与冲击,2010,(07): 28-32,234.

[6] 李鹏.汽车试验道路强化系数的研究[D].吉林大学硕士学位论文,2006.

The Stress Analysis of Suspension Spring under Automobile Random Road Motivation

Chen Shuang1, Liang Jingang2
（1.Automobile & Transportation Engineering College, Liaoning University of Technology, Liaoning Jinzhou 121001; 2.LiaoShen industrial group in the 724 factory, Liaoning Shenyang 110045）

On the basis of eight degrees of freedom vehicle dynamic model and road surface time-domain model of random input with four-wheel-related, the random stress time course of suspension springs is derived. It is decomposed and reconstructed for many layers through discrete dyadic wavelet transform. And rain-flow counting method is used to analyze the stress process after decomposition. The distribution of the stress frequency is obtained. The research conclusion will offer new conference to fatigue damage analysis of automobile suspension spring.

Vehicle; Suspension spring; Random stress; Wavelet analysis; Rain-flow counting

U463.3

A

1671-7988（2015）12-53-05

陈双，博士，讲师，就职于辽宁工业大学汽车与交通工程学院，研究方向为车辆系统动力学及控制。