非恒定磁链幅值给定的永磁同步电机直接转矩控制
唐 校,杨向宇,赵世伟,胡致远
(华南理工大学 电力学院,广东 广州 510641)
0 引言
直接转矩控制(DTC)直接将定子磁链和转矩作为控制对象,由于不需要进行磁场定向和坐标变换,相对于矢量控制,其结构简单,转矩的动态响应更快。作为一种现代电机控制技术,直接转矩控制受到不少学者的关注,也取得了很多成果[1-8]。
传统的直接转矩控制一般将定子磁链幅值设定为一个恒定值[5-6],为了维持这个恒定的定子磁链,往往需要定子电流提供较大的无功分量,这在电机的运行过程中,不能使系统的运行性能最优,常常会使效率降低。
已有一些学者针对非恒定磁链给定进行研究,例如文献[7]中提出了一种无磁链环直接转矩控制方案,目的是获得最快的电机转矩响应。本文着重从电机运行效率出发,研究永磁同步电机直接转矩控制中如何设置合适的定子磁链给定值,以期实现定子电流的最优控制。仿真和实验结果证实了算法的有效性。
1 传统永磁同步电机直接转矩控制
直接转矩控制最初采用的是开关表模式,但是这种模式存在开关频率不固定、转矩脉动大的缺点。后来有学者提出了基于空间矢量调制的直接转矩控制方案(SVM-DTC),有效地解决了原来开关表模式存在的问题。
1.1 定子磁链观测
直接转矩控制的对象是定子磁链和电磁转矩,因此,定子磁链的准确观测是实现直接转矩控制的必要前提,当观测不准确时将导致电机运行性能的下降,甚至使电机不能运行。常用的定子磁链观测方法有电流模型和电压模型2类。电流模型需要转子位置信息和坐标变换,有违直接转矩控制结构简单的特点;电压模型不需要转子位置信息,结构更为简单,是一种本质意义上的无位置传感器控制方法。
定子磁链电压观测模型如下:
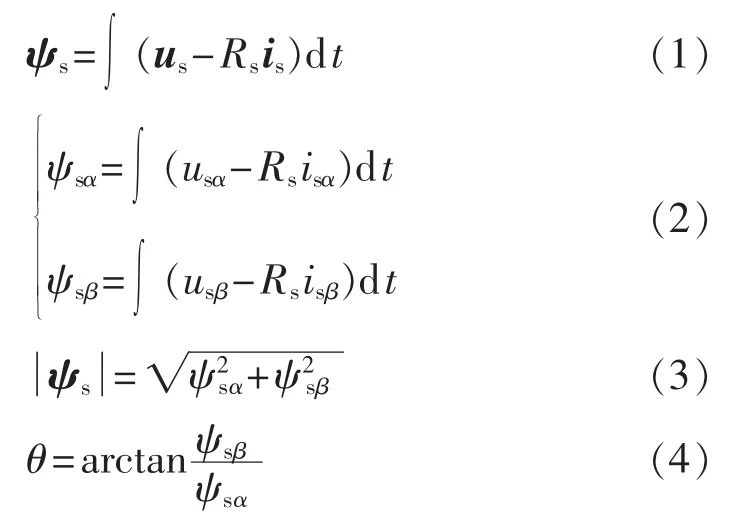
其中,ψs为定子磁链矢量;us和is分别为定子电压矢量和电流矢量;ψsα和ψsβ为定子磁链在两相静止坐标系(αβ 坐标系)中的坐标分量;usα和 usβ为电压矢量的坐标分量;isα和isβ为电流矢量的坐标分量;Rs为定子电阻;为定子磁链幅值;θ为定子磁链的相位。
但是采用式(1)的纯积分电压模型会存在初始值问题和积分饱和问题,一种简单有效的解决方案是采用低通滤波器代替纯积分器,然后再对输出结果进行补偿[9-11],从而解决低通滤波器引入的幅值误差和相位误差。其原理如下:
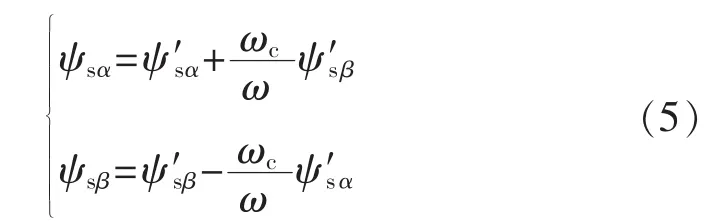
低通滤波器的表达式为:
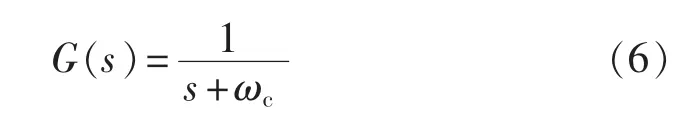
其中,ω为电机电角频率;ωc为低通滤波器的截止频率;ψ′sα和 ψ′sβ为通过低通滤波器后的定子磁链分量。
1.2 基于空间矢量脉宽调制的直接转矩控制
采用空间矢量脉宽调制(SVPWM)合成参考电压可以使逆变器开关管的频率固定,减小电磁转矩的脉动,关键是如何在直接转矩控制的系统中准确获得参考电压矢量。已有一些文献针对此提出了各自的方案[12-15],本文采用文献[12]所描述的算法。 整个系统的结构如图1所示。
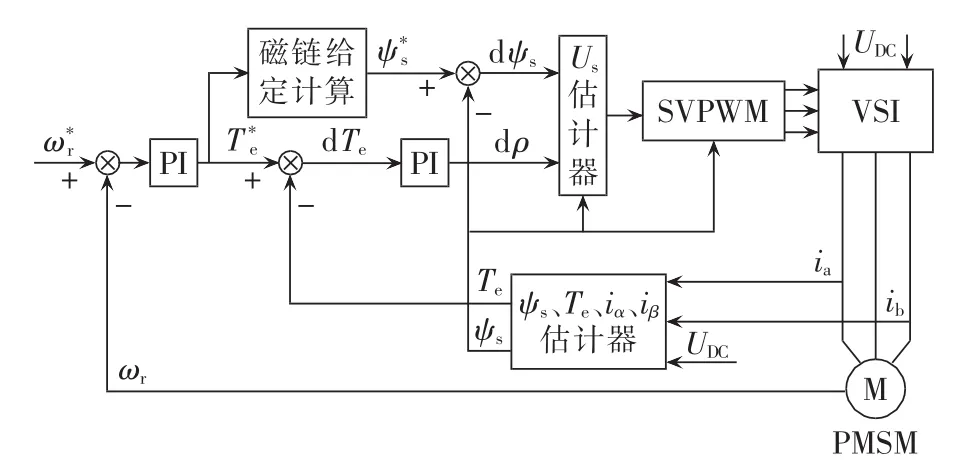
图1 永磁同步电机 SVM-DTC系统结构图Fig.1 Block diagram of SVM-DTC system for permanent magnet synchronous motor
图1中,ψs*是定子磁链幅值给定,dρ表示负载角的增量。参考电压矢量的获得方法如下所示:
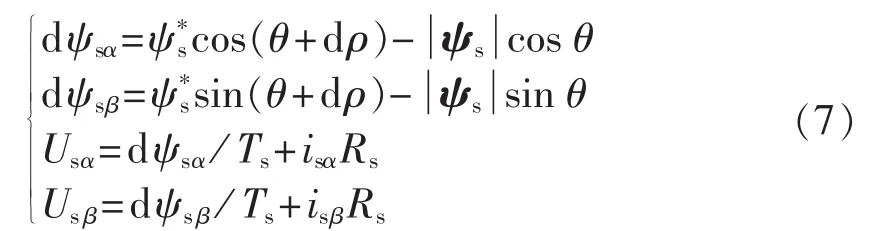
其中,Usα和Usβ为参考电压矢量在αβ坐标系中的坐标分量。
2 非恒定磁链幅值给定的永磁同步电机直接转矩控制
在永磁同步电机不同的运行工况下,电机的输出转矩是不一样的,如果保持定子磁链幅值恒定,势必会使电机的运行效率降低。因此,可以根据电机的运行状况,给定不同的定子磁链幅值,以优化电机的运行性能。
永磁同步电机的定子磁场由2个磁场合成[16],分别是永磁体产生的励磁磁场ψf和定子电流矢量is产生的电枢磁场Lsis。以表贴式永磁同步电机为例,定子电流矢量和磁链矢量的示意图如图2所示。
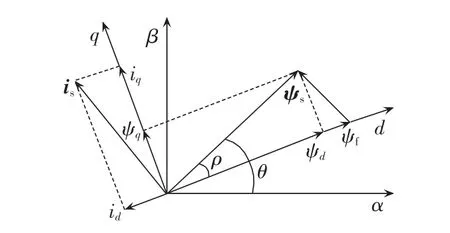
图2 表贴式永磁同步电机的定子电流和磁链矢量Fig.2 Stator currents and flux vectors of surface-mounted permanent magnet synchronous motor
图2中ψd和ψq表示定子磁链在两相旋转坐标系(dq坐标系)中的坐标分量,id和iq是电流矢量在dq坐标系中的坐标分量,ρ为负载角。表贴式永磁同步电机在两相旋转坐标系(dq坐标系)下的转矩表达式为:

其中,Te为电磁转矩;p为电机的极对数。由式(8)可以得到:

对于表贴式永磁同步电机,定子电流最优控制方式为 id=0 的控制方式[16],此时,is即为 iq。 在这种情况下,定子电流矢量的幅值表达式为:

由于定子磁链幅值的表达式为:
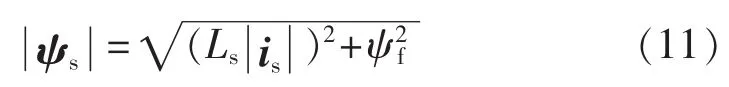
将式(10)代入式(11)得到定子电流最优控制时的定子磁链幅值给定为:
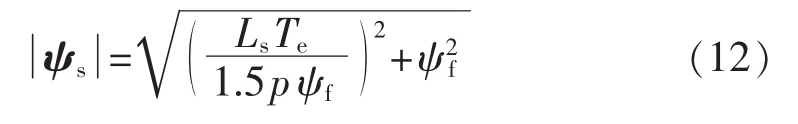
3 仿真及实验分析
3.1 仿真分析
本文在MATLAB环境中搭建永磁同步电机直接转矩控制仿真模型,对比分析传统的恒定磁链幅值给定和本文提出的非恒定磁链幅值给定时的电机运行特性。永磁同步电机的参数如下:极对数为4,定子电阻为0.5 Ω,交、直轴电感均为4.5 mH,永磁磁链为 0.124 Wb,转动惯量为 0.00095 kg·m2。
仿真模型中给定转速为100 rad/s。图3—6为电机带1 N·m负载时的仿真波形,图7—10为电机带5 N·m负载时的仿真波形。图3和图7为定子磁链圆,图4和图8为三相定子电流波形,图5和图9为dq坐标系下电流波形,图6和图10为转速和转矩波形。其中(a)为给定定子磁链幅值0.14 Wb时的情形,(b)为本文提出的随电机输出转矩需要动态给定定子磁链幅值的情形。
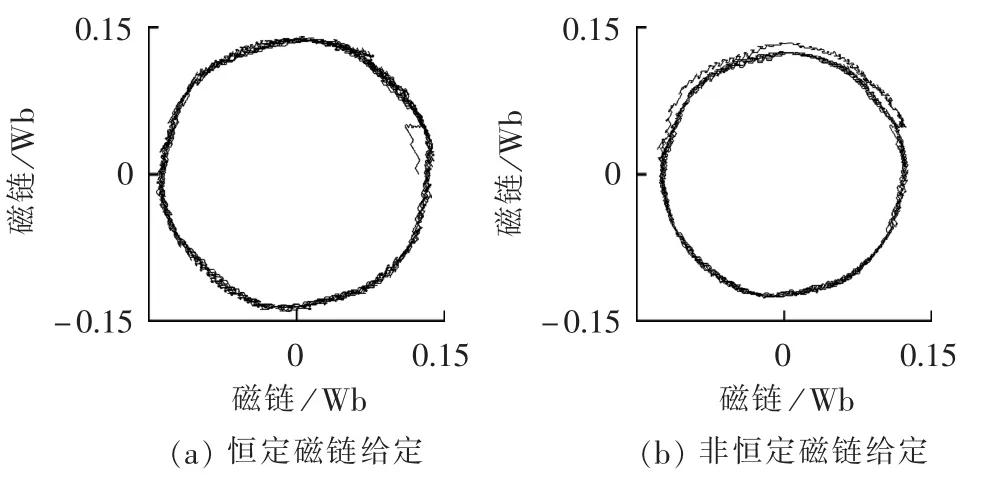
图3 负载1 N·m时定子磁链圆Fig.3 Stator flux circle when load is 1 N·m
由图3和图7可以发现,采用恒定定子磁链给定方式的直接转矩控制在不同的负载条件下的定子磁链大小是一样的,而本文的方式是根据转矩大小设定定子磁链幅值的给定值。对比定子电流波形可以发现,采用恒定定子磁链幅值给定的永磁同步电机直接转矩控制时,其id的值不等于0,三相定子电流幅值较大;采用非恒定磁链幅值给定的方案后,其id的值约等于0,三相定子电流幅值较小。在相同负载条件下,电机定子电流的减小意味着电机的运行效率较高。由图6和图10可以发现两者的转矩和转速响应一致,即采用非恒定磁链幅值给定的直接转矩控制保持了原来直接转矩控制转矩响应快的特点。
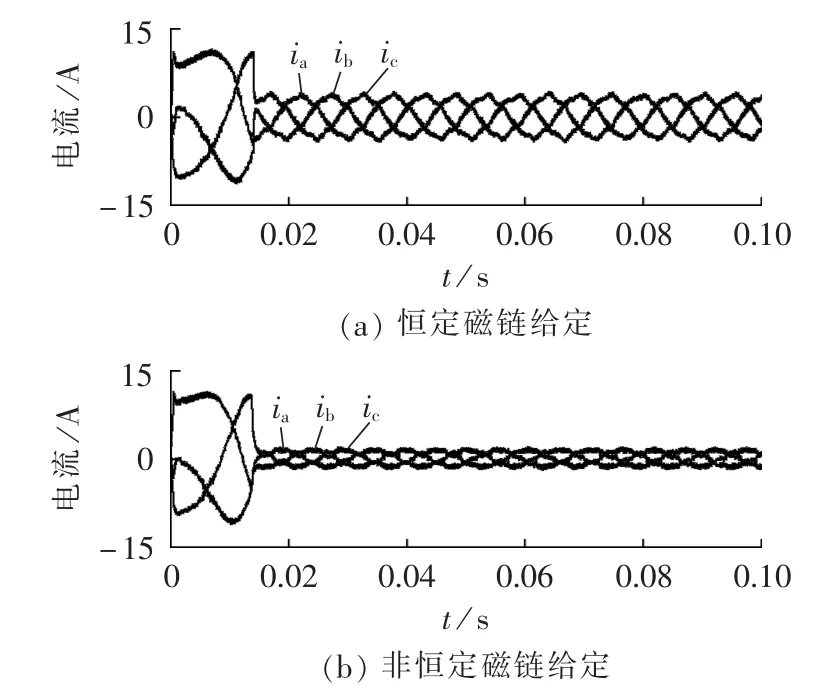
图4 负载1 N·m时三相电流仿真波形Fig.4 Simulative waveforms of three-phase currents when load is 1 N·m
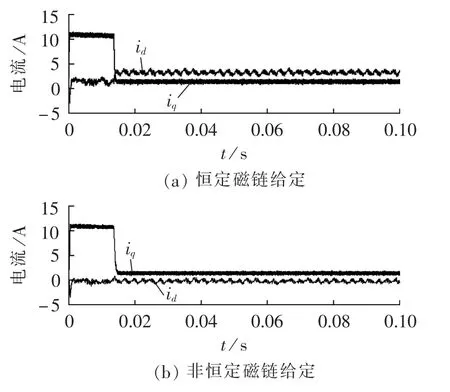
图5 负载1 N·m时dq轴电流仿真波形Fig.5 Simulative waveforms of dq axes currentswhen load is 1 N·m
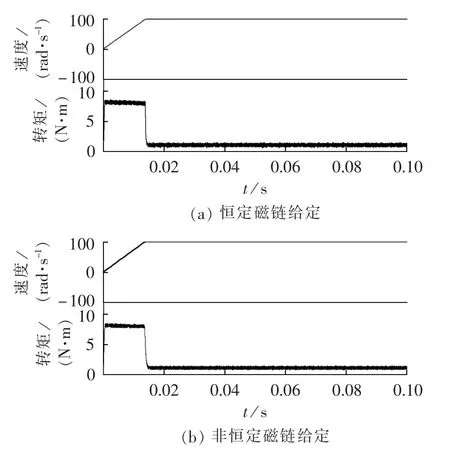
图6 负载1 N·m时转速和转矩仿真波形Fig.6 Simulative waveforms of speed and torquewhen load is 1 N·m
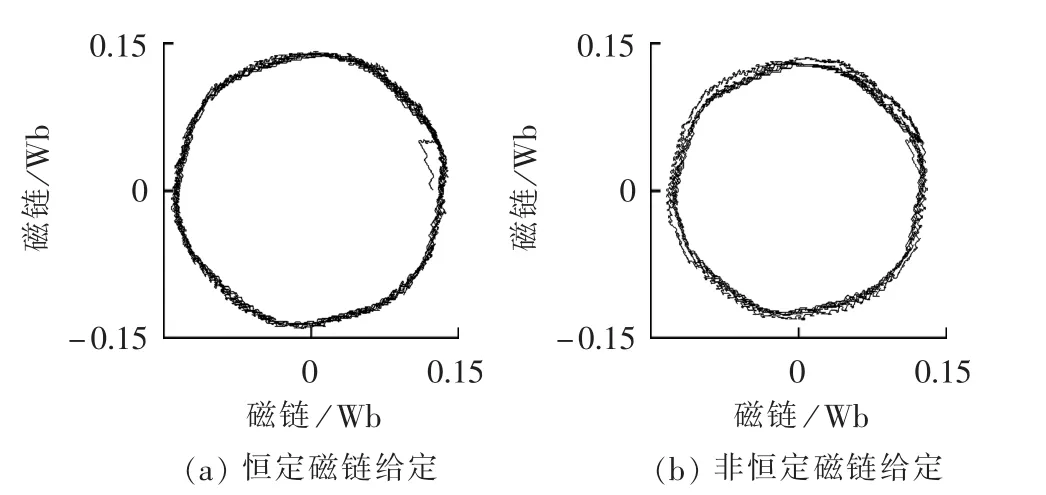
图7 负载5 N·m时定子磁链圆Fig.7 Stator flux circle when load is 5 N·m
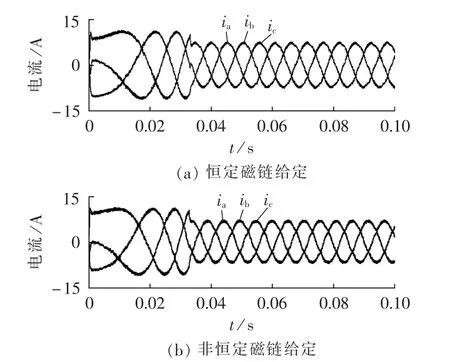
图8 负载5 N·m时三相电流仿真波形Fig.8 Simulative waveforms of three-phase currents when load is 5 N·m
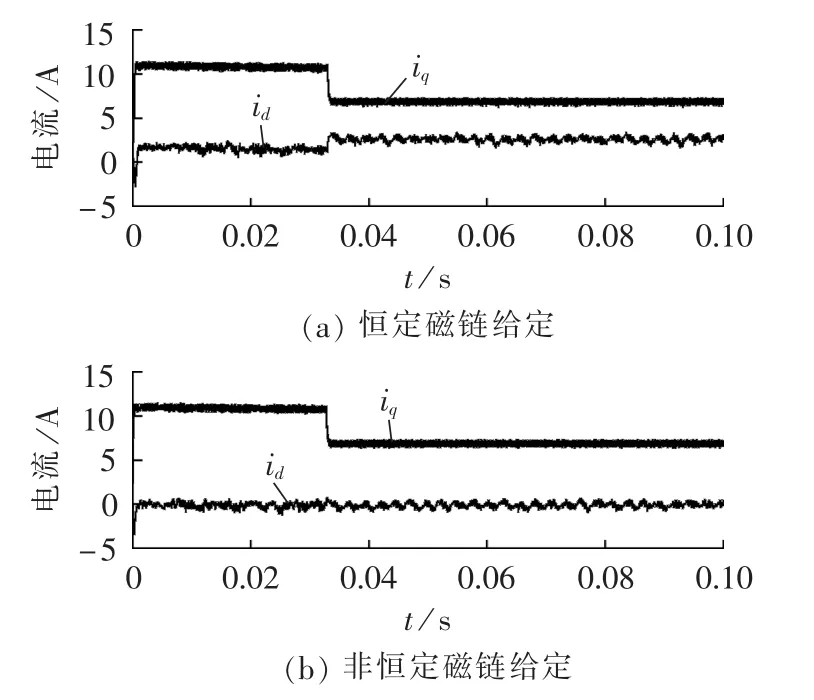
图9 负载5 N·m时dq轴电流仿真波形Fig.9 Simulative waveforms of dq axes currents when load is 5 N·m
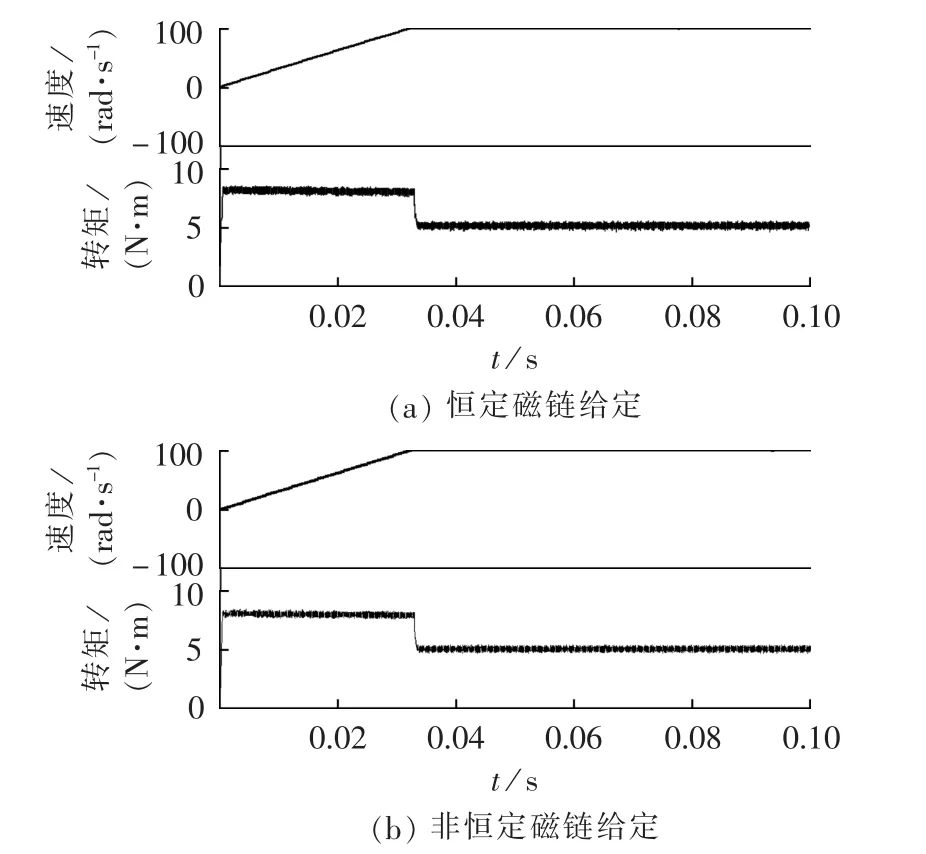
图10 负载5 N·m时转速和转矩仿真波形Fig.10 Simulative waveforms of speed and torque when load is 5 N·m
3.2 实验分析
本文搭建了永磁同步电机直接转矩控制实验平台,主控芯片采用TI公司的TMS320F2812,逆变电路采用的是三菱智能功率模块PS21865,最大工作频率为20 kHz。考虑模块工作的稳定性,将主电路工作频率设定为15 kHz。为了安全起见,直流侧电压设为50 V。永磁同步电机的参数与仿真模型中参数一致,采用磁粉制动器模拟电机的负载,通入不同的直流电流会产生不同的负载转矩。
需要说明的是,根据转矩值实时计算磁链的给定,涉及平方运算和开方运算,通过处理器实时计算将耗费大量的运算时间,实际处理时是采用查表的方式进行的。由于实验平台没有数模转换(DAC)模块,因此一些运算量的显示通过TI公司的DSP集成开发环境CCS(Code Composer Studio)中的图形显示功能查看,处理的方式是在程序中设置数组来存储变量的值,包括磁链波形和id、iq电流波形,数组大小为60。
图11是定子磁链在两相静止坐标系中α轴分量。图12和图13为示波器采集到的电机两相(U相和V相)电流波形。图14和图15为id和iq电流值,所显示的数值大小为电流值经AD转换后的数值,1 A电流所对应的AD数值为683。
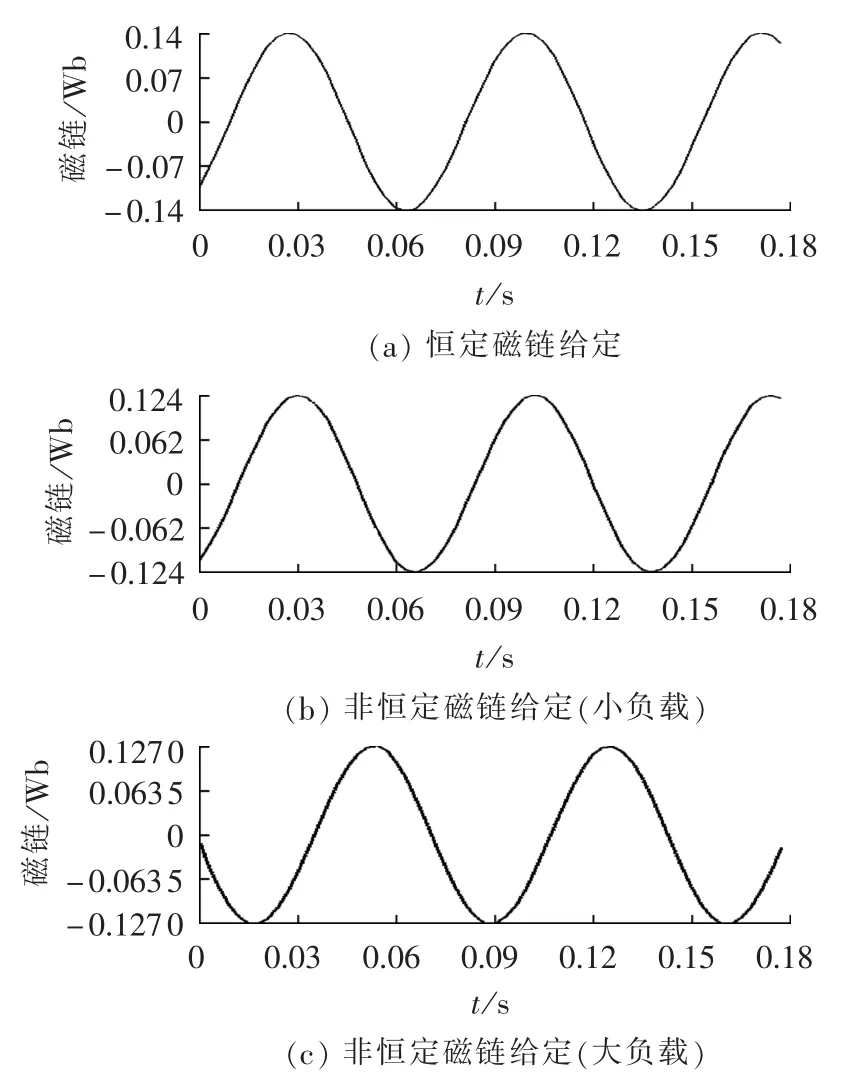
图11 定子磁链α轴分量波形Fig.11 α-axis stator flux waveforms
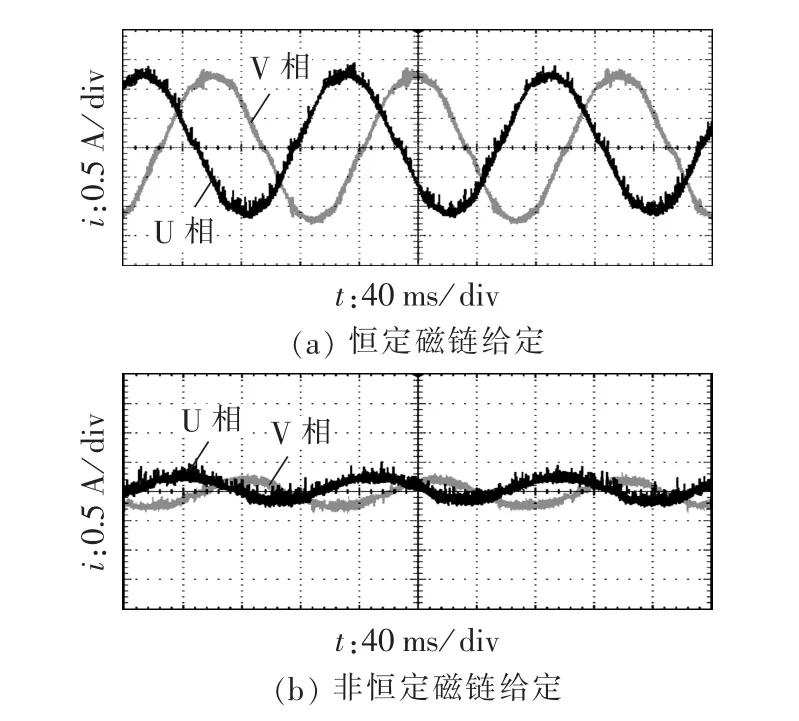
图12 小负载时两相电流波形Fig.12 Two-phase current waveforms when load is light
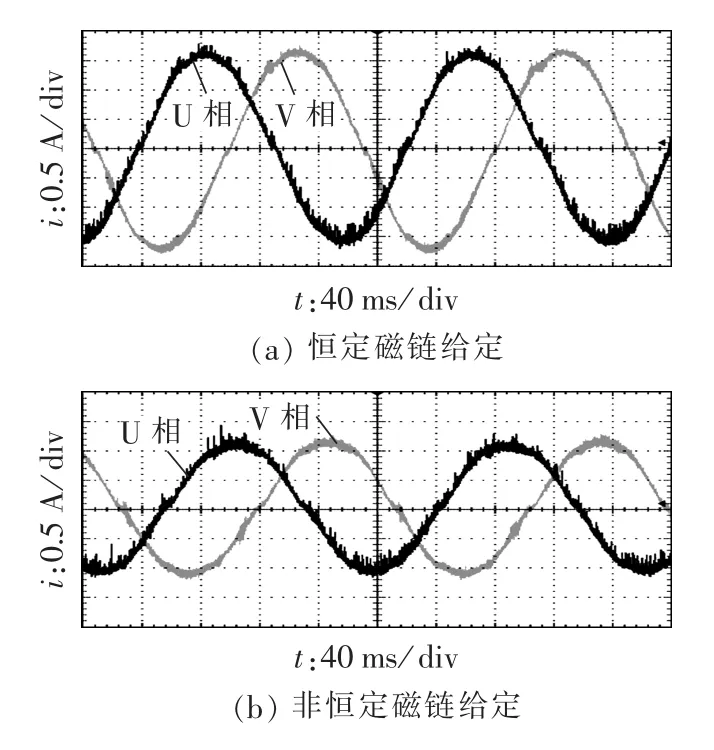
图13 大负载时两相电流波形Fig.13 Two-phase current waveforms when load is heavy
上述实验结果所测得的波形均是电机带不同负载运行于稳定状态时的结果。采用恒定磁链幅值给定时,往往需要产生较大的无功分量,结果是定子电流幅值较大,进行dq分解后的直轴电流较大,图14(a)中id值均为650左右,对应实际电流值为0.95 A左右,图15(a)中id值均为710左右,对应实际电流值约为1.04 A。当根据负载状态采用非恒定磁链幅值给定时,其 id值近似为 0,图14(b)和图15(b)中 id值看上去波动较大,主要是坐标分量较小的原因。因此根据转矩大小设定定子磁链给定值能够基本实现定子电流最优控制,使电机在不同的运行工况下保持较高的效率。实验结果与仿真结果一致。
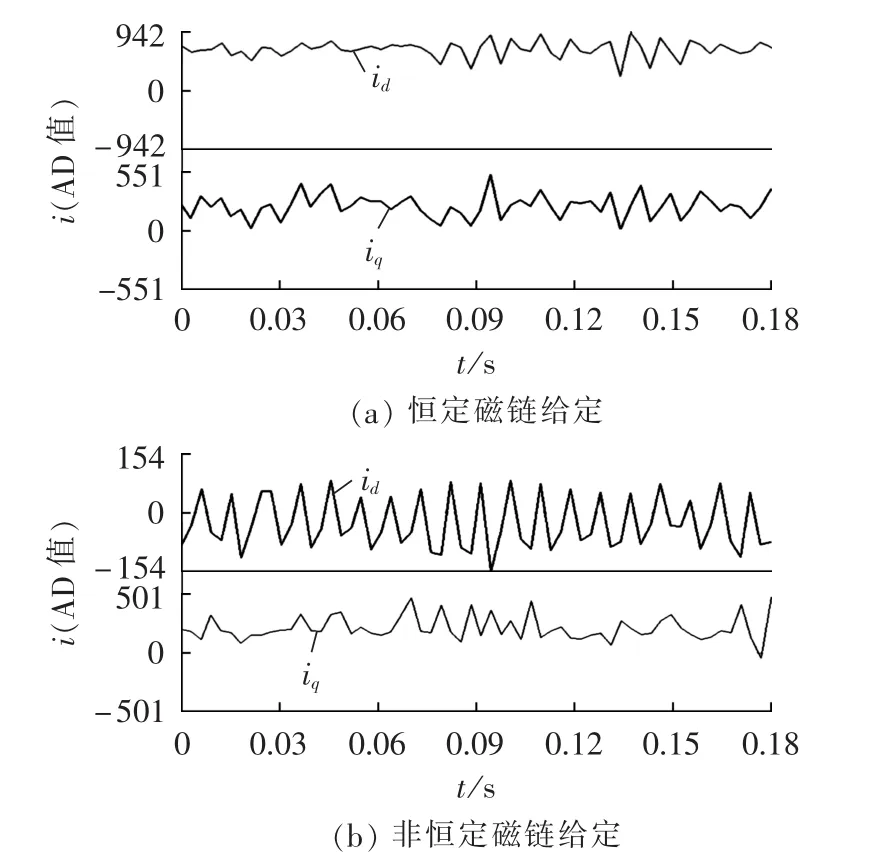
图14 小负载时dq轴电流波形Fig.14 dq axes current waveforms when load is light
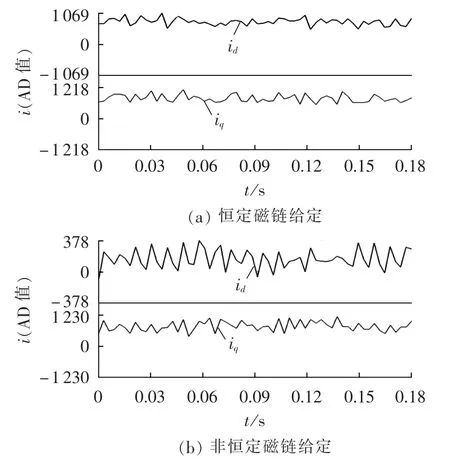
图15 大负载时dq轴电流波形Fig.15 dq axes current waveforms when load is heavy
4 结论
永磁同步电机直接转矩控制的控制目标包括定子磁链幅值和电磁转矩,传统的方法中将定子磁链幅值设定为恒定值,在电机实际运行中效率较低。本文以表贴式永磁同步电机为例,研究了定子电流最优控制方案所对应的定子磁链幅值给定方法,采用这种非恒定磁链幅值给定的方案后,可以实现id=0的控制效果,提高了电机的运行效率。

