考虑转捩的气冷涡轮气热和热弹耦合计算

李 涛，冯 宇，马海红，边 昕，黄洪雁，韩万金

(1.哈尔滨工业大学 能源科学与工程学院，150001哈尔滨;2.中国船舶重工集团 第703研究所，150078哈尔滨)

最近几年，一种流体固体耦合求解方法即气热耦合方法(CHT)被用来解决涡轮的传热问题［1-7］.气热耦合计算中一个关键性因素是湍流模型的封闭，在存在转捩的气冷涡轮流场计算中考虑转捩能提高传热计算的精度［7-9］.王强等［7］采用代数AGS转捩模型和一方程间歇因子输运方程转捩模型研究了不同的转捩模型对气热耦合精度的影响.曾军等［8］采用双方程转捩模型完成了对MARKII和VKI两个高压涡轮导叶叶栅外换热系数的计算，验证了采用转捩模型后，计算的换热系数与实验值吻合更好.在有冷却结构的涡轮叶片中，由于其与高温燃气和冷却气体相接触，导致在叶片的内部形成较大的温度梯度，产生较大的热应力和热变形，减少叶片寿命.为提高涡轮的安全可靠性，气热、热弹多物理场耦合的计算方法逐渐被用来解决工程中遇到的强度问题［9-13］.

本文在多面体网格上分别采用有限体积法和有限元方法建立了气热、热弹多物理场耦合计算平台.NS方程的求解采用隐式LUSGS求解器，湍流模型采用SST模型和SST+Gama-Theta转捩模型.热弹计算的有限元方法采用四面体网格的二次单元十结点的高精度插值函数.最后通过MARKII型叶片5411工况的算例和圆筒的解析解对气热、热弹耦合平台进行了验证，分析了转捩模型对传热计算的影响，分析了转捩对热应力计算的影响.

1 计算方法

1.1 流场的控制方程及离散格式

NS方程在笛卡儿坐标系下的积分形式为

式中:守恒变量W=［ρ，ρu，ρv，ρw，ρE］T;∂Ω为控制体的边界;Ω为控制体;Fc为无黏通量;Fv为黏性通量，具体形式见文献［14］．

为增强程序对壁面低速流动的适应性和收敛性，采用了预处理技术，预处理后的控制方程为

式中:Wp为原始变量，WP=［p，u，v，w，T］T，Γ为预处理矩阵采用Weiss-Smith形式.

采用有限体积法对方程进行空间离散，在任意一个网格单元i上，将式(1)离散得

式中:Ni是与单元i相邻的所有单元的集合;im是单元i和单元m的公共面;Sim是面im的外法向量，其模等于面im的面积．

本文采用二阶精度的空间插值方法，用加权最小二乘法求解变量的梯度，并且用Venkatakrishnan限制器［15］来提高稳定性，对流项通量格式为AUSM+格式，黏性项采用中心差分.求解方法为LUSGS隐式方法，由于非结构化网格编号的无序性，有些网格周围会只有编号大于它的网格或只有编号小于它的网格，这样会导致Gauss-Seidel迭代退化为Jacobi迭代，影响计算效率，为此采用了网格重排序方法［16］.

1.2 导热方程的隐式求解

直角坐标系下的非稳态导热方程为

式中:cp为固体的定压比热容，k为固体的导热系数．

采用有限体积法在单元i上离散式(2)得

式中:Dn，im为法向扩散项;Dc，im为交叉扩散项，其具体形式及扩散项的隐式处理方法见文献［17］．最后用GMRES［18］方法求解离散后的方程组.

1.3 Gama-Theta双方程转捩模型

Gama-Theta转捩模型是由间歇因子和转捩动量厚度雷诺数两个参数的输运方程组成.

1.3.1 间歇因子输运方程

间歇因子的输运方程为

式中需要用到Flength和Reθc，Flength的作用是来调节转捩区的长度，Reθc为失稳雷诺数．Flength和Rθc都是的函数，具体形式见文献［19］．

1.3.2 转捩动量厚度雷诺数输运方程由于Reθt是由自由流参数得到的，在边界层中使用转捩经验关系式不合理，因此需要将边界层外的Reθt输运到边界层内，为此采用了转捩动量厚度雷诺数输运方程，其形式为

式(3)中各项参数的意义见文献［19］.

1.3.3 分离流转捩模型及对SST的修改

为预测分离引起的转捩，对间歇因子进行修改:

最后用γeff代替γ作为最终有效的间歇因子，当出现分离时，γsep会迅速增长，当γsep＞γ时，分离流转捩模型被激活，当转捩完成时通过Freattach控制γeff趋近于1．用γeff修改SST模型k方程的生成项和耗散项，即

1.4 求解热应力的有限元方法

利用最小位能原理［20］建立有限元方程为

式中:K为结构整体刚度矩阵;P为结构结点载荷列阵;K和P分别由单元刚度矩阵Ke和单元等效结点载荷列阵Pe集合而成，其中

式中:B为应变矩阵，D为弹性矩阵，Ke为10×10的分块矩阵，它的每一块为3×3的矩阵为

热膨胀只产生正应变，剪切应变为零，因此这种由热变形引起的应变可以看作是物体的初应变ε0，其表达式为

温度应变引起的载荷项Pe为

根据单因素试验分析结果得出，影响检测结果的因素分别为：激励信号的幅值和频率、降温速度以及热处理；但仅依靠单因素试验无法确定各影响因素对检测结果的影响程度以及试验的最优条件，因此，本文采取正交试验方法对各因素进行综合分析，从而得出最佳的试验条件。

计算出位移变量，然后通过ε=Bae求得应变量ε，最后求得物体所受的应力:

式中ae为单元e的结点位移列阵．

1.5 耦合方法

本文的气热耦合过程通过分别单独求解流场流动和叶片导热并在交界面上传递温度或热流来实现，此类耦合方法为弱耦合.交界面数据传递的通量守恒性对气热耦合的稳定性和精度有一定的影响，因此采用面积加权类的插值方式［21］来保证通量守恒，本文采用直接耦合方法［22］，该方法需要流固两侧互相传递温度.弱耦合的求解效率低于强耦合，为提高计算效率，初场采用壁面绝热条件下收敛的计算结果.

热弹耦合计算采用单向耦合的方法，由于文中的有限元方法只能适用于四面体网格，而用于气热耦合的网格为多面体混合网格，所以需要将气热耦合计算的边界温度插值到应力计算的四面体网格上，先计算出四面体网格的温度场再进行应力计算.

2 计算结果及分析

2.1 气热耦合计算

本文选用文献［23］中MARKII型叶片5411号实验工况，进出口边界条件见表1、2，ptotin为入口总压，Ttotin为入口总温，Tuinlet为入口湍流度，poutlet为出口静压，min为冷却管的入口质量流量.本文的计算网格是ICEM软件生成的六面体和五面体的混合非结构化网格(图1)，外流场、冷却流体和叶片网格单元数分别为45万、24万、17万.对壁面附近的边界层的网格进行了加密(如图1(d)所示)，壁面第一层网格到壁面的距离为10 μm，网格增长因子为1.12，保证第一层网格的y+值基本位于1左右，这是由于本文所用到的SST+Gama-Theta模型和SST湍流模型都是低雷诺数湍流模型，因此需要壁面第一层网格位于边界层的黏性底层.叶片的材料为ASTM标准的310不锈钢(0Cr25Ni20)，密度ρ=8 030 kg/m3，定压比热容cp=502 J/(kg·K)，导热系数为λ=

16.9 W/(m·K).

表1 叶片的运行条件

表2 冷气孔的运行条件

图1 MARKII的网格示意图

图2为用SST+Gama-Theta模型计算的流道中径处截面的马赫数云图.可以看出，5411工况为跨音速流动，气流从前缘开始膨胀加速，压力不断下降，在x/c=0.43处产生一道马赫数为1.5的强激波，从图3叶片中径壁面压力分布曲线可见，此处压力有一个明显的突升，随后气流继续膨胀，在x/c=0.95处产生了一道马赫数为1.2的弱激波.从强激波位置的速度矢量放大图中可以看出5411工况发生了边界层的分离.从图3可看出，SST模型和Gama-Theta模型计算的压力在压力面和吸力面激波之前的位置相差不大，与实验值基本吻合.

图2 中径处的马赫数分布

图3 叶片中径近壁面处的压力分布

通过观察间歇因子在如图4所示的3个到壁面不同距离(10、80、200 μm)处的分布可以看出，由于本文的计算网格在近壁面进行了加密，y+值在1左右，属于黏性底层的范围，因此dx=10 μm处的间歇因子比较小(0.005-0.010).从图中可以看出，当距离从10～80 μm变化时，在压力面的大部分和吸力面靠近前缘的部分间歇因子的增长比较小，除了前缘点在0.75之外，其余部分仍然在0.005～0.010，这说明该区域的边界层仍然为层流;x/c≥0.43区域的间歇因子从0.2增长到1.0，这说明此距离处的边界层流态已经为湍流，因此80 μm距离处的间歇因子的变化证明了边界层在x/c=0.43处发生了转捩，由层流转变为湍流，从而导致了该距离处的涡黏系数与SST模型有较大差异.从图5中可以看出，在0.43≥x/c≥-1.00的区域，转捩模型计算的涡黏系数明显低于SST模型.转捩点的位置与之前的激波位置重合，这表明激波引起的逆压力梯度导致了边界层的分离从而诱导了转捩的发生.

图4 叶片中径处的间歇因子分布

图5 叶片中径dx＝80 μm处的涡黏系数分布

图6给出了叶片中径处表面换热系数的分布，换热系数的计算公式为

图6 叶片中径处表面的换热系数分布

由于边界层中垂直壁面的对流作用比较弱，因此边界层与壁面之间的换热主要靠热量的扩散，而涡黏系数的大小直接影响着温度扩散项的系数.涡黏系数增大会导致扩散系数变大，从而增强燃气和叶片之间的传热，导致计算的温度升高.从图5的涡黏系数分布可见，在转捩点之后的位置计算的涡黏系数有一个比较大的峰值，导致此处燃气对叶片的加热作用过强，由图6、7可看出，在该处两种模型的计算温度和实验值误差较大，约为7%，换热系数的误差在40%，这同时证明了两种湍流模型受到激波的干扰，在该处计算的涡黏系数过大.由于Gama-Theta模型在压力面的大部分区域和吸力面靠近前缘的区域计算的涡黏性系数比SST模型小，导致相应计算的温度也较低，温度的误差在2%左右，而且计算的换热系数精度更高，分布趋势与实验值吻合更好，说明Gama-Theta模型在该区域计算的边界层流态与真实流动相符合，计算的涡黏性系数更合理.

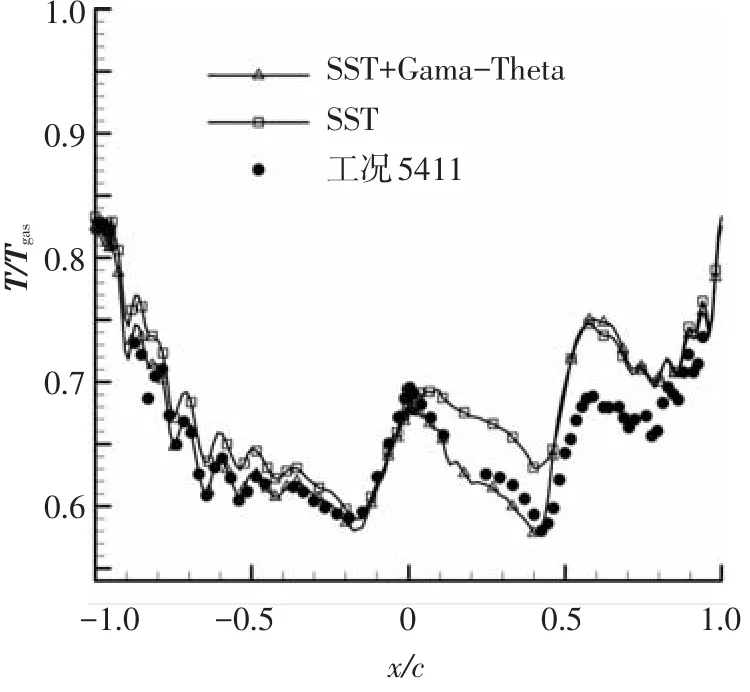
图7 叶片中径处表面的温度分布

2.2 热弹单向耦合计算

2.2.1 圆筒热应力解析解验证

采用文献［24］的有限长空心圆筒的解析解来验证热应力计算的精度.圆筒的内径ri为0.05 m，外径re为0.1 m，长度为0.5 m，材料属性同MARKII叶片一样，网格单元数为38 824，外表面温度为0，内表面温度为30 K，圆筒两端为绝热边界，并且无位移约束条件，温度在圆筒内沿半径r的分布函数为

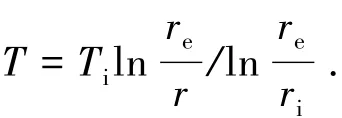
此算例的轴向应力σz、径向应力σr、周向应力σθ的解析解:

通过图8在x轴上总位移的分布曲线可以看出，计算的位移和解析解吻合很好，误差在1%的范围，总位移从圆环内径开始逐渐增大，在x=0.084 m附近达到最大值.从图9中3个方向的应力分布曲线可以看出，周向应力和轴向应力大小差不多，径向应力最小.由于圆筒内外表面无约束条件，所以内外表面在径向上自由膨胀，因此产生的径向应力基本为0.从图9中可以看出，周向和轴向应力在内表面附近为负值，这说明内径单元热膨胀在周向和轴向受到相邻单元的挤压作用力;在外表面附近受到的周向和轴向应力为正值，说明在热膨胀对该处的单元产生了拉伸的作用.3个应力的计算解和解析解基本吻合，说明本文应力计算模型的精度较高，在给定精确解温度的前提下，能够准确地计算出位移和热应力.

图8 位移分布的解析解和计算解对比

图9 圆筒的热应力沿径向的分布

2.2.2 MARKII叶片单向热弹分析

在气热耦合收敛后，将计算的MARKII叶片的温度边界插值到进行热应力计算的网格上，网格单元数为159 864，通过有限体积法求解得到新网格上的温度场，然后进行热应力的计算，所加的约束条件为上下端壁固定，即位移为0，其他边界为自由边界.叶片材料选用ASTM标准的310不锈钢(0Cr25Ni20)，泊松比为 ν=0.3，弹性模量E=2.0×105MPa，材料的线性膨胀系数 α0=1.3×10-5.建立叶片应力求解模型是比较复杂的过程，文献［15］主要研究的是MARKII叶片的传热特性，只是给出了简单的几何模型，所以在叶片两端简单地加位移为0的条件会导致叶片沿径向方向以及在根部和顶部膨胀受到不合理的约束，会导致叶片整体的应力值过高，偏离正常范围.为此，将初始温度设定为400 K，相当于将叶片均匀预热到400 K然后进行安装，降低了叶片两端受到的过大约束，使得热应力的分布趋势更加合理，这样做同样能对比分析转捩对热应力的影响.

图10为叶片中径截面的等效应力分布，本文采用的等效应力为von mises应力，等效应力是最大等效应力失效理论下的一种，常常用来预测具有延展性材料的应力状态，等效应力关系式为

式中 σ1、σ2、σ3为主应力．

图10 叶片中径处截面的von mises应力分布

热应力主要是由于热膨胀受到约束、冷热温差导致受热不均匀和结构的各向异性产生，由图10可以看出，叶片最小的等效应力位于前缘附近的三根管的区域，通过图11的温度云图可以看到，该处由于距离三根管很近，被冷却得比较充分，温度都在400 K左右，温度梯度较小，分布比较均匀，因此热应力比较小.热应力的最大值并没有位于尾缘，虽然该处的温度是最高的，但是由于该处离叶片的表面很近，热膨胀受到的约束比较小，而且该处的温度分布比较均匀.从图11中可以看出，由于采用Gama-Theta模型后计算的温度要比SST模型低，叶片的温度分布相对均匀，因此采用Gama-Theta模型后计算的热应力要比SST模型的小，在转捩区两者相差100 MPa左右.由于Gama-Theta模型计算的温度场与实验值吻合更好，因此采用该模型后计算的等效应力更符合真实情况.采用转捩模型能提高气热耦合的精度，同时也能更准确预测叶片的热应力和变形，能更好地预测叶片的安全可靠性.

图11 叶片中径处截面的温度分布

3 结论

1)隐式的流场和固体场求解方法、预处理技术、守恒型交界面插值方法、壁面网格加密、采用能预测转捩的湍流模型等是构建高精度、稳定的气热耦合平台的必要措施.

2)在涡轮的叶栅传热计算中，考虑转捩对主流参数的影响不大，计算的压力与全湍流的SST模型差别较小，与实验值基本吻合.采用Gama-Theta模型有效地提高了传热计算的精度，在压力面的大部分和吸力面转捩点之前的区域，温度误差在2%左右.

3)基于二次单元的有限元方法计算的热应力和位移与解析解误差很小.Gama-Theta模型计算的温度在转捩区比SST模型低20～40 K，导致计算的热应力在该位置相差100 MPa左右.由于Gama-Theta模型能提高传热计算的精度，因此能更好地预测叶片的安全可靠性.

［1］BOHN D，TUMMERS C.Numerical 3-D Conjugate flow and heat transfer investigation of a transonic convectioncooled thermal Barrier coated turbine guide vane with reduced cooling fluid mass flow［C］//Proceedings of ASME Turbo Expo 2003.Atlanta:ASME，2003:1-8.

［2］KUSTERER K，BOHN D，SUGIMOTO T，et al.Conjugate calculations for a film-cooled blade under different operating conditions［C］//Proceedings of ASME Turbo Expo 2004.New York:ASME，2004:1-10.

［3］KULASEKHARAN K，PRASAD B.Conjugate heat transfer analysis in the trailing region of a gas turbine vane［J］.Heat Transfer Engineering，2010，31(6):468-484.

［4］XIE G A，SUNDEN B.Conjugate analysis of heat transfer enhancement of an internal blade tip-wall with pin-fin arrays［J］.Journal of Enhanced Heat Transfer，2011，18(2):149-165.

［5］DONG Ping，WANG Qiang，GUO Zhaoyuan，et al.Conjugate calculation of gas turbine vanes cooled with leading edge films［J］.Chinese Journal of Aeronautics，2009，22(2):145-152.

［6］SILIETI M，KASSAB A，DIVO E.Film cooling effectiveness:comparison of adiabatic and conjugate heat transfer CFD models［J］.International Journal of Thermal Sciences，2009，48(12):2237-2248.

［7］王强，郭兆元，周驰，等.考虑转捩的跨声速气冷涡轮叶片气热耦合计算［J］.航空动力学报，2009，24(12):2703-2710.

［8］曾军，卿雄杰.涡轮叶栅外换热系数计算［J］.航空动力学报，2008，23(7):1198-1204.

［9］MAZUR Z，ROSSETTE A H，ILLESCAS R G，et al.Analysis of conjugate heat transfer of a gas turbine first stage nozzle［C］//Proceedings of ASME Turbo Expo 2005.Nevada:ASME，2005:1-8.

［10］AMEZCUA A C，CZERWIEC Z M，MUÑOZ A G，et al.Thermomechanical transient analysis and conceptual optimization of a first stage bucket［J］.Journal of Turbomachine，2011，133(1):011031.

［11］BOLAINA C，TELOXA J，VARELA C，et al.Thermomechanical stress distributions in a gas turbine blade under the effect of cooling flow variations［J］.Journalof Turbomachine，2013，135:064501.

［12］郭兆元，王强，冯国泰.涡轮气热弹耦合计算模型与算例［J］.航空学报，2009，30(2):213-219.

［13］彭茂林，杨自春，曹跃云.应变场强法在涡轮盘-片结构寿命预测中的应用［J］.中国电机工程学报，2011，31(26):97-102.

［14］BLAZEK J.Computational fluid dynamics principles and applications［M］.Kidington:Elsevier，2001.

［15］MICHALAK K，GOOCH C O.Limiters for unstructured higher-order accurate solutions of the euler equations［C］//46th AIAA Aerospace Sciences Meeting and Exhibit.Reno:AIAA，2008:776-790.

［16］SHAROV D，NAKAHASHI K.Reordering of 3-D hybrid unstructured grids for vectorized LU-SGS navierstokes computations［C］//13th Computational Fluid Dynamics Conference.Reno:AIAA，1997:131-138.

［17］商立英，非结构化网格上非稳态导热问题的求解［D］.南京:南京理工大学，2006.

［18］LUO H，BAUM J D，LOHNER R.A fast，matrix-free implicit method for compressible flows on unstructured grids［J］.Journal of Computational Physics，1998，146(2):664-690.

［19］LANGTRY R B，MENTER F R.Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes［J］.AIAA Journal，2009，47(12):2894-2906.

［20］王勖成.有限单元法［M］.北京:清华大学出版社，

2003.

［21］刘鑫，陆林生.拼接网格通量守恒插值算法研究［J］.计算机应用与软件，2012，29(2):275-278.

［22］王强，提高气冷涡轮气热耦合计算精度的计算方法研究［D］.哈尔滨:哈尔滨工业大学，2009.

［23］HYLTON L D，MILHEC M S.，TURNER E R，et al.Analytical and experimental evaluation of the heat transfer distribution over the surface of turbine vanes［R］.Washington:NASA，1983.

［24］李维特，黄保海，毕仲波.热应力理论分析及应用［M］.北京:中国电力出版社，2004.