面向在轨测量任务的伴飞机器人三维仿真系统

吴剑威，崔继文，史士财，谭久彬

(1.哈尔滨工业大学超精密光电仪器工程研究所，150080哈尔滨;2.机器人技术与系统国家重点实验室(哈尔滨工业大学)，150080哈尔滨)

随着空间技术的不断发展，对于未来航天器长寿命周期和高可靠性的要求将越发趋于严格.为保证航天器在复杂的空间环境中运行更加持久稳定，在轨检测目前已成为航天器故障诊断与威胁警告的关键技术手段.同时，在空间组装、系统升级和后勤支持等领域中，在轨检测技术也具有非常广泛的需求［1］.美国的多项研究计划如 XSS 计划［2］、MiniAERCam计划［3］等都促进了在轨检测领域相关技术的发展.由于空间机器人在轨具有良好的机动性，并往往搭载带有传感器的多自由度机械臂系统，因此可作为待测航天器贴近与伴飞的新型检测平台，利用机械手携带的多种非接触传感器，如电磁检测传感器等，通过专门设计空间伴飞机器人的测量轨迹，可实现安全、可行、有效的近距离检测，获得特定的检测结果.根据检测任务需求，空间机械臂在轨检测过程主要包括如下4个过程:1)空间机器人系统飞行接近航天器使空间机械臂贴近待测航天器表面;2)机械臂跟踪检测轨迹并进行航天器待测表面的测量;3)完成测量任务，机械臂停靠;4)载体姿态的重稳定.为了节约能源、避免碰撞，机械臂在跟踪检测轨迹的过程中通常需要关闭载体的姿控系统使载体处于自由漂浮状态.

目前很多学者对自由漂浮空间机器人末端轨迹规划方法进行了相关研究，如文献［4-9］，这些文献中对于轨迹规划方法中数学模型都是建立在简单连杆机构基础上的，方法的仿真验证也都是采用不直观的数值曲线仿真.而对于实际在轨检测的空间伴飞机器人系统，机械臂每一个连杆都具有复杂的结构，并不是简单连杆所能表示的.当机械臂末端探测器跟踪上述方法所规划的测量轨迹时，很可能造成臂杆之间或机械臂与载体之间发生碰撞.因此在机械臂所规划的运动执行之前必须利用三维图形仿真验证以保证机械臂的安全工作.另外利用三维图形仿真还可以对新提出的轨迹规划算法进行可行性验证，与单纯的数值仿真相比，仿真结果更加直观.本文基于虚拟现实方法，提出一种高真实感空间机器人三维仿真系统，该系统可实现仿真数据与虚拟环境实时交互等多种操作.

1 基于虚拟现实技术的伴飞机器人模型建立

虚拟现实技术是一种可以创建和体验虚拟世界的计算机仿真系统［10］.该技术是三维仿真领域的一个重要发展趋势，其中包含了多媒体技术、传感器设备、网络、人机接口技术、仿真技术及电脑图形设计等多个前沿技术领域，这种多个技术领域交互配合的前沿技术领域是很具有挑战性的.在机器人研究领域中虚拟现实技术通常应用于空间机器人的遥操作系统［11］.本文空间机器人三维仿真平台的开发就是基于虚拟现实技术，依靠计算机系统生成的一种模拟环境.

1.1 三维实体几何模型建立

三维仿真实体的整个建模过程总体来说就是对其进行详细的数学分析描述，尽量把实体信息化和数字化，这样有益于计算机程序读取分析，然后由处理器创建一个尽量贴近实体的虚拟几何模型.详细来讲此过程可分为实体建模、框架搭建、表面处理这3种不同细致程度的类型［12］.其中实体建模更符合计算机平台的需求.由于该模型是真实物体具体的计算机数字描述，因此能由内到外的表现出原实体形状，进而解决了三维实体现实感官的二维显示问题.本文以实体建模软件对空间机器人系统进行实体建模，见图1.该模型为串联机器人运动连杆结构，可以划分为7个模块.包括1个载体模块、3个双关节模块(连杆1、连杆3、连杆5)、两个臂杆模块(连杆2、连杆3)，1个末端探测器模块.

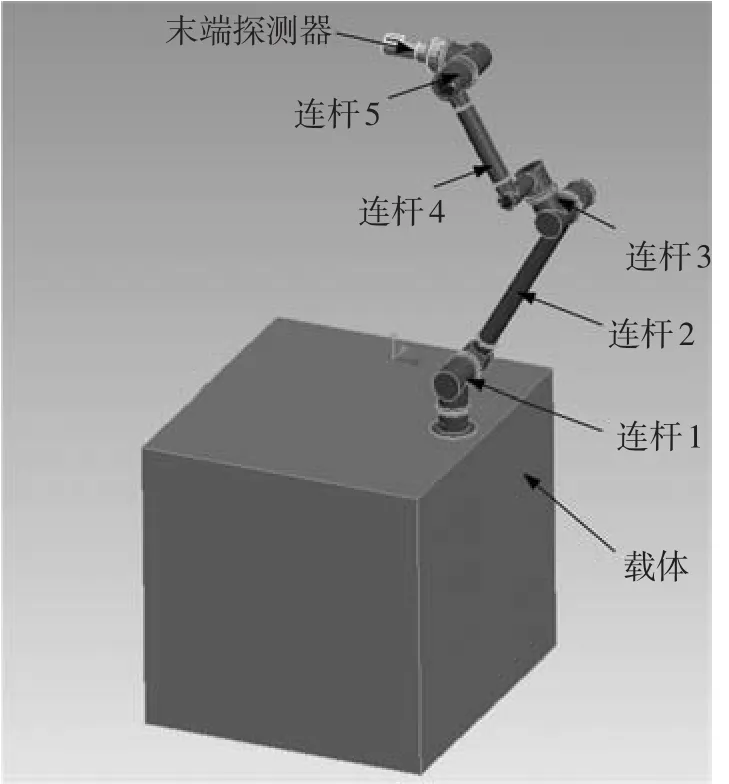
图1 空间伴飞机器人实体建模

1.2 定位模块建模

机械臂图形仿真系统的设计中单单能实现高仿真视觉效果是远远不够的，必须还要具有实体的运动功能.在Open Inventor标准的动态虚拟仿真场景设计中，机械臂的运动是根据一系列数字化指令所产生的，而指令需要借助坐标系作为参考来实现.因此每个需要活动的实体都要有一个相应的参考点，否则运动指令不会有效.为了建立与实体运动相关的坐标系，通常采用的方法是在机械臂的旋转轴位置处引入一个定位模块.根据定位模块，使得仿真系统可以拾取运动部件参考系，从而通过指令驱动实体产生运动.定位模块虽然不是机械臂零部件，但却是必需的，一般都是轴对称或者中心对称的几何实体.

仿真系统设计的定位模块见图2.该定位模块只能是通过拉伸创建实体特征.虽然从几何的角度看，旋转特征也能够建立对称实体，但是在Open Inventor环境下系统无法识别旋转特征的中心轴，从而无法建立相应的坐标系.

1.3 仿真平台三维场景的建立

将建立的三维实体几何模型导入Open Inventor构建的虚拟场景中，完成机器人系统逻辑位置的组装，其逻辑结构见图3.虚拟现实场景中，各实体模块逻辑位置的确定也可以说是创建场景所有基本节点的过程.本系统中每个节点分别对应机械臂的一个零部件(包括定位部件)，整体来说都是上层节点管理下层节点，而定位部件的运动坐标的参考点的确定和变换也是由这种分隔符群组节点来决定.由上述逻辑关系建立的三维仿真场景见图4.

图2 定位模块建模

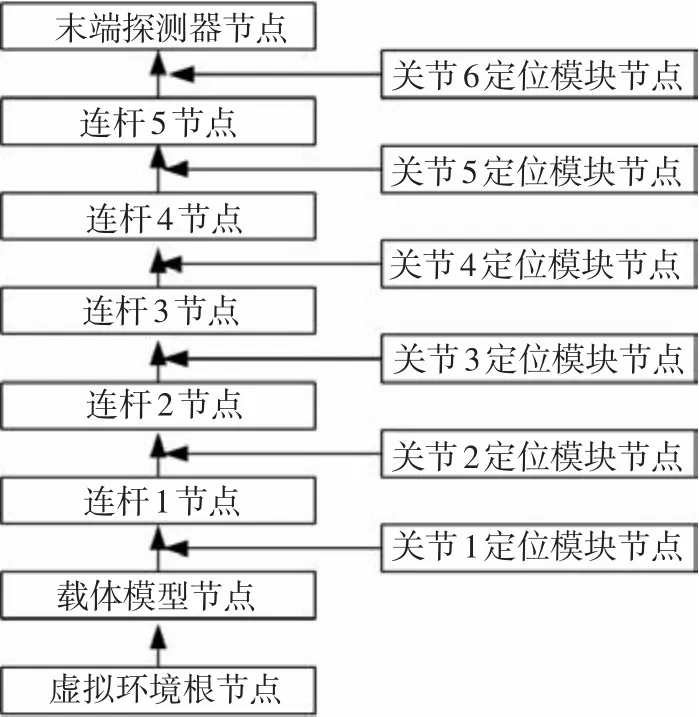
图3 虚拟环境中机械臂组装的逻辑结构

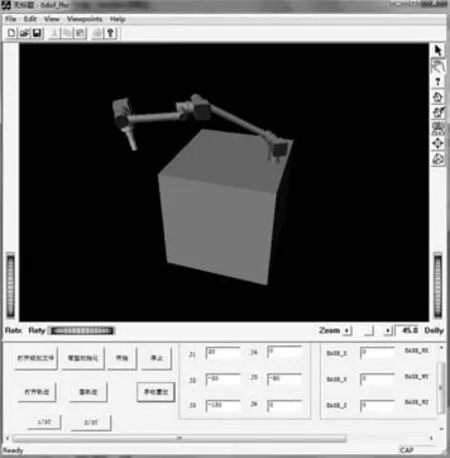
图4 基于虚拟现实技术的空间伴飞机器人三维仿真场景

1.4 自由漂浮空间机器人运动学建模

图5为自由漂浮空间机械臂一般模型，其中n自由度的机械臂和机械臂自身的载体航天器构成了整个平台．该系统由n+1个刚体杆组件构成．其中杆件0表示空间机器人的载体，转动关节i+1连接第i和第i+1个杆件．

由空间机器人的一般模型可知，机械臂各杆件质心和机械臂末端的位置矢量可以分别为

式中:ai为从关节i指向杆件i质心的位置矢量，ai∈R3;bi为从杆件i质心指向关节i+1的位置矢量，bi∈R3．

由此微分可得各杆件质心线速度为

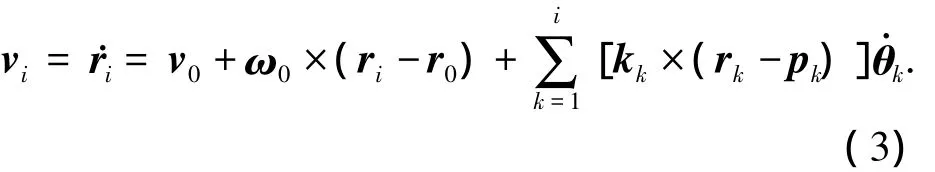
式中:v0为载体质心的线速度矢量，v0∈R3;ω0为载体质心的角速度矢量，ω0∈R3;θ为关节i的旋转角度，θ∈Rn;k为关节i旋转方向的单位矢量．

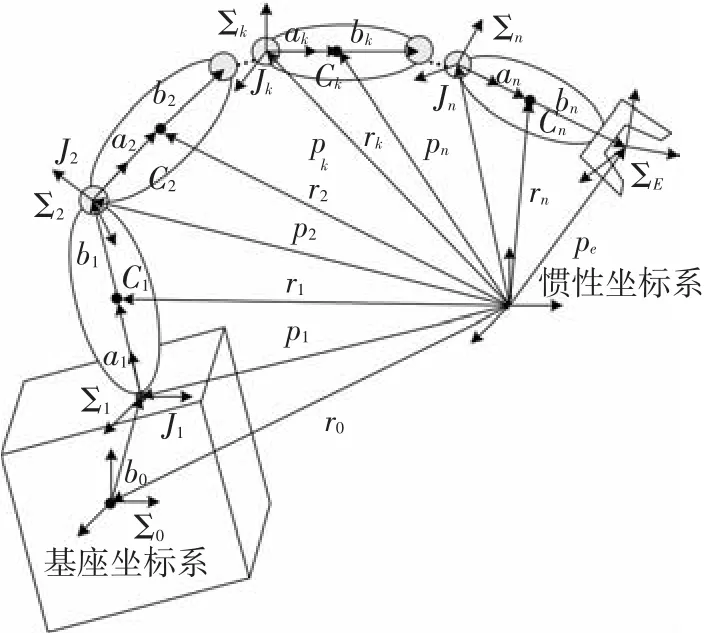
图5 漂浮基空间机械臂的一般模型

机械臂末端的线速度为

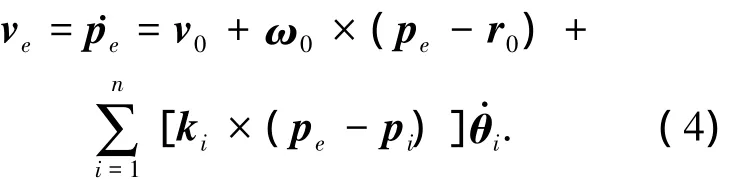
各杆件质心角速度为

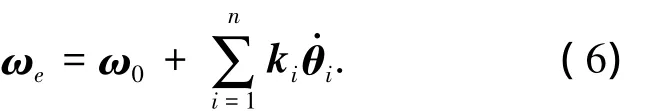
机械臂末端姿态的角速度为将式(4)和式(6)写成矩阵形式，有

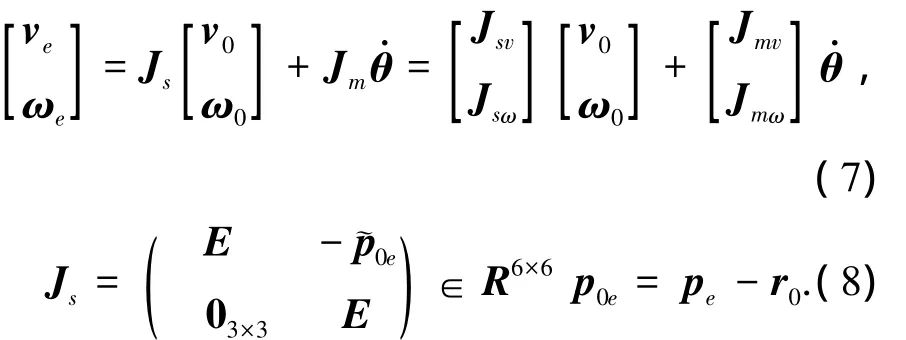
式(7)为空间机器人的运动学方程.其中Js为与载体运动有关联的雅可比矩阵;Jsv，Jsω分别为Js关于载体速度和角速度的分块矩阵;E为单位矩阵;0m×n为m×n的零矩阵．其中定义向量r=［x，y，z］的操作m可表达为而Jm为与机械臂运动相关的雅可比矩阵，

Jmv、Jmω分别为Jm关于速度和角速度的分块矩阵．

Jm与地面固定基座机器人雅可比矩阵相同，Jm可表达为

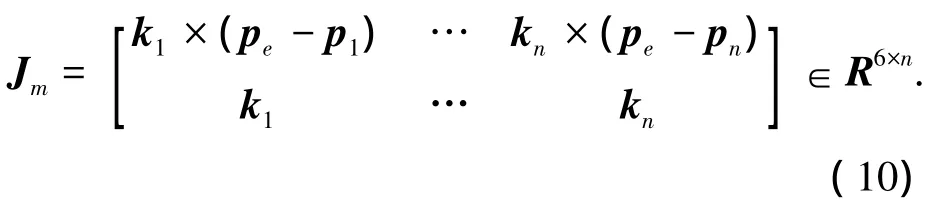
2 仿真平台数据传输与存储模块设计

仿真系统的通信程序采用消息机制的异步套接字阻塞与非阻塞的工作方式作为底层接口，然后按照客户端模式进行开发.如果把阻塞工作模式应用于机械臂三维仿真平台中，那么在实现I/O操作前，执行数据传输操作的通信模块不会立刻把程序运行的结果返回调用进程或者是主线进程，从而使得上层程序得到控制权，而是从始至终在进程中运行直到网络上实时仿真数据出来.例如，在客户端上接收网络传递的数据时，通常情况下程序常常采用的recv函数传递往来的数据.如果经过一段时间后，数据包仍没有通过网络传递过来，那么该客户端中的上层程序就会一直阻塞在该函数的进程中，其他模块的程序也将不会继续执行，该客户端的主线程也将会被暂停运行.不止如此，在许多情况下使用阻塞工作方式也将会影响网络通信的性能.如果采用Winsock函数的客户端在非阻塞工作模式下工作，不管网络状态如何，程序往往都立即检测并把数据传递的状态返回.另外，在采用Winsock函数传递时，不仅仅可以获得操作结果的通知，也可以通过该通知检验数据传递的正确性.

本文所建立的空间机器人三维仿真平台网络通信程序采用非阻塞工作方式，如图6所示.综合运用了消息传递与异步套接字响应机制所需具有的网络事件筛选功能，注册一些FD-WRITE、FDREAD、FD-CLOSE FD-ACCEPT等常用的网络事件，利用多线程技术尽可能减少阻塞的可能性.

另外，三维仿真系统设计了本地文件存储模块.该模块主要用于离线作业和在线实时仿真运算的存储、输出、交流演示等.存储文件以文本文件保存.每次进行数据存储时，文本文件以追加的方式打开.如果是第一次存储或者原存储文件已删除，则重新创建存储文件.

图6 虚拟现实三维仿真平台的网络通信客户端模块

3 系统仿真

仿真的任务是对机械臂末端探测器跟踪圆轨迹进行三维虚拟现实仿真.这是空间检测机器人的一种常规任务.

对于空间机器人圆弧轨迹的跟踪，需要规划末端的速度.定义圆弧轨迹的圆心坐标系为{Ⅰc}，其原点定义在圆心处，圆弧轨迹位于坐标系{Ⅰc}的x，y轴所在平面内．{Ⅰc}到惯性坐标系的旋转矩阵为Tc．规划轨迹的圆周角随时间变化函数为θc(t)，如果机械臂末端跟踪轨迹为一个闭合的圆轨迹，则边界条件应满足

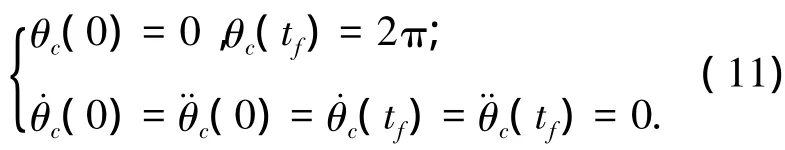
为了满足跟踪轨迹的平滑性，·θc(t)也采用梯形规划．空间机械臂末端线速度为位置pe的微分pe，位置矢量为

式中:rc为圆轨迹的半径．

机械臂末端的初始笛卡尔位姿为(2.18，-0.15，0.88，-3.09，-0.52，-2.95)，初始关节角为(175°，-40°，-120°，0°，240°，5°).在跟踪的过程中令机械臂末端的姿态保持不变，圆轨迹半径rc=0.35 m，圆心坐标系到惯性系的转移矩阵为

因此将末端速度pe代入1.3节的运动学模型，可规划出空间伴飞机器人末端探测器跟踪上述圆轨迹时机械臂各关节的角位移，如图7所示．

上述机器人运动规划的虚拟现实三维模拟仿真如图8所示，根据该的仿真结果可以方便地看出当机械臂末端探测器实现从初始位置跟踪封闭的圆轨迹直到回到初始位置的运动后，其载体的位置和姿态并没有回到初始状态，也就是说载体的位置与姿态与机械臂末端位置没有关系，而与机械臂运动的历史有关，即呈现出典型的非完整特性［13］.根据该仿真结果，可使研发人员在空间伴飞机器人的圆测量轨迹设计、仿真中对机械臂实际工作状态(如轨迹跟踪、载体姿态变化等)得出更为直观的结果.

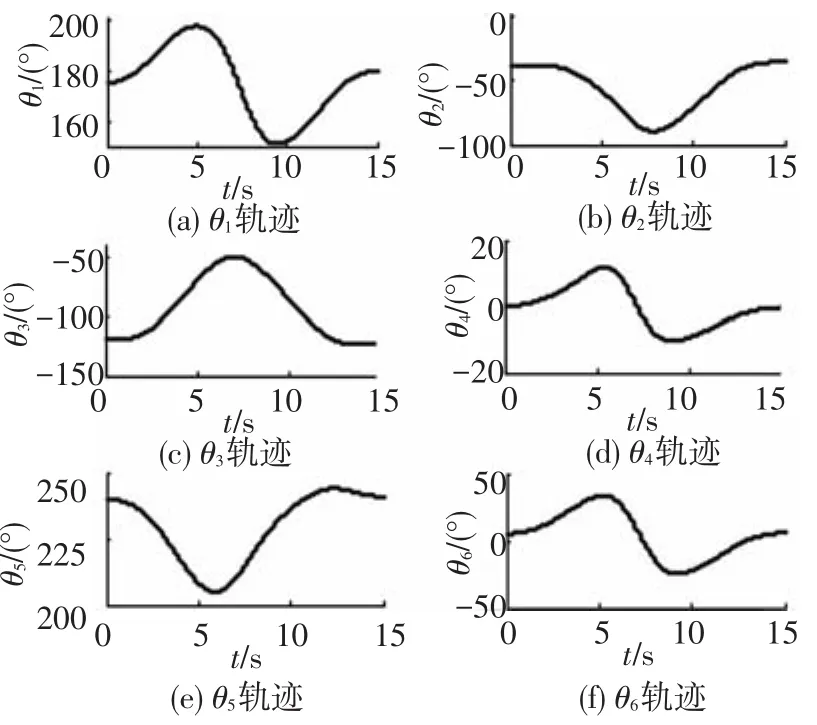
图7 末端探测器跟踪圆轨迹时机械臂各关节的角位移

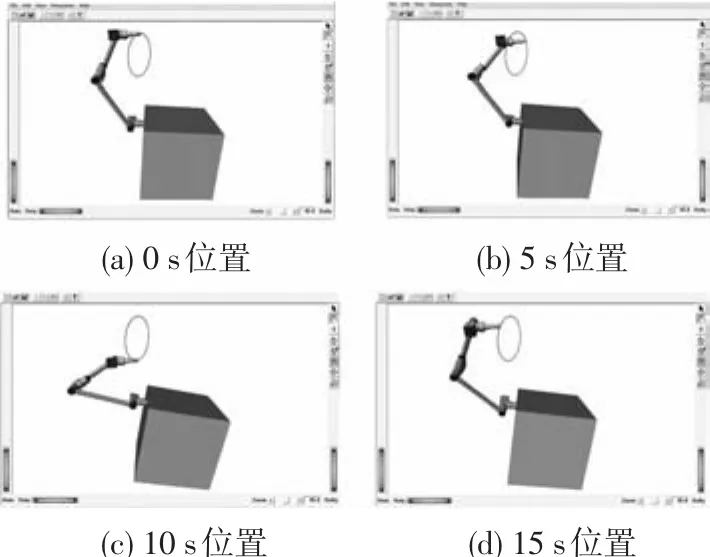
图8 空间伴飞机器人对圆测量轨迹跟踪的仿真

4 结 论

1)基于虚拟现实技术，建立了空间伴飞机器人三维实体模型，并针对模型的运动坐标系建立了模型的定位模块，构建了仿真平台的三维场景.该仿真系统可实现空间伴飞机器人在轨测量的可视化仿真.

2)建立了三维仿真系统的数据传输与文件存取模块，实现在线或离线仿真时，仿真数据与图形界面的实时交互.

3)基于空间机器人运动学模型对空间伴飞机器人跟踪圆轨迹进行轨迹规划，并利用本文建立的三维仿真系统对该轨迹规划进行了仿真.通过仿真可以直观地得到空间伴飞机器人跟踪圆轨迹时的运动规律，验证了三维仿真系统的有效性.

［1］史建伟，蔡远文，李岩.在轨检测研究综述［J］.兵工自动化，2011，30(6):59-62，83.

［2］MADISON R W.Micro-satellitebased， on-orbit servicing work at the air force research［C］//Aerospace Conference Proceedings.Big Sky， Montana:IEEE，2000:215-225.

［3］FREDRICKSON S E，DURAN S，MITCHELL J D.MiniAERCam inspection robot for human space missions［C］//Space 2004 Conference and Exhibit.San Diego，California:IEEE，2004.

［4］ZARAFSHAN P，ALI S，MOOSAVIAN A.Dynamics modelling and hybrid suppression control of space robots performing cooperative object manipulation ［J］.Communi-cations in Nonlinear Science and Numerical Simulation，2013，18(10):2807-2824.

［5］AMIT K，PUSHPARAJ M P，SUKAVANAMA N.Trajectory control of a two DOF rigid-flexible space robot by a virtual space vehicle［J］.Robotics and Autonomous Systems，2013，61(5):473-482.

［6］TORTOPIDIS I，PAPADOPOULOS E.On point-to-point motion planning for underactuated space manipulator systems［J］.Robotics and Autonomous Systems，2007，55(2):122-131.

［7］HU Xiaoping，ZUO Fuyong.Research and simulation of robot trajectory planning in joint space［J］.Applied Mechanics and Materials，2012，103:372-377.

［8］KANDIL A A，BADREDDIN E.A new method for direct and point-to-point robot trajectory planning in narrow spaces［C］//IEEE International Conference on Control Applications/International Symposium on Intelligent Control.St Petersburg，Russia:IEEE，2009:1738-1743.

［9］徐文富，强文义，李成，等.自由漂浮空间机器人路径规划研究进展［J］.哈尔滨工业大学学报，2009，41(11):1-12.

［10］邹湘军，孙健，何汉武，等.虚拟现实技术的演变发展与展望［J］.系统仿真学报，2004，16(9):1905-1909.

［11］胡海鹰，李家炜，王滨，等.虚拟现实技术在机器人臂/灵巧手遥操作中的应用［J］.系统仿真学报，2004，16(10):2305-2308.

［12］KANG K，TAREL J，FISHMANET R，et al.A linear dual-space approach to 3D surface reeonstruction from occluding contoursusing algebraic surface［C］//Proceedings of International Conference on Computer Vision(ICCV).Vancouver，BC，Canada:IEEE，2009:356-364.

［13］NAKAMURA Y，MUKHERJEE R.Nonholonomic path planning of space robots via a bidirectional approach［J］.IEEE Transactions on Robotics and Automation，1991，7(4):500-514.