基于改进PCA的人脸识别算法
李云彤 ,黄 山 ,徐海明
(1.四川大学 电气信息学院,四川 成都 610065;2.四川大学 计算机学院,四川 成都 610065)
0 引言
人脸识别是通过分析人的面部特征来自动进行身份鉴定的一种生物特种识别技术。相较于红膜识别、DNA识别、指纹识别,人脸识别具有友好性强、全自动化、设备成本低等优点,在安全验证系统、金融业务、罪犯调查、人机交互等领域都有着极其重要的作用和意义。人脸识别是一门综合性较强的技术,涵盖了计算机视觉、图像处理、模式识别、机器学习、心理认知等众多学科。以人脸为目标,也将推动这些基础研究的发展、融合和应用[1]。20世纪90年代以来,人脸识别已成为国内外研究的热点。在此基础上,学者们发表了大量研究文章,同时催生了相关期刊和学术会议,也产生了一批人脸识别的商业系统。一个完整的人脸识别系统可以分为
以下几个阶段,如图1所示。
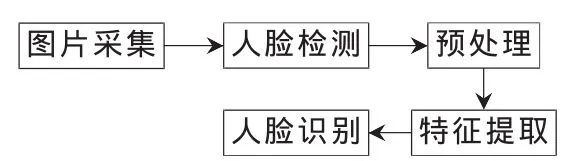
图1 人脸识别系统组成
当前人脸识别方法主要包括基于几何特征的人脸识别、神经网络方法、隐马尔科夫模型等方法、支持向量机(SVM)、主成分分析法(PCA)等。基于几何特征的方法[2]具有直接、计算快、存储要求低等优点,但识别正确率较低,通常不单独使用。神经网络用网络的联想能力重构人脸[3],但需要较多样本且计算复杂度高。隐马尔科夫模型方法根据人脸特点建立马尔科夫模型并进行HMM训练[4],取得了较好的识别效果。支持向量机[5]作为有效的工具已经广泛应用到了人脸识别领域的分类阶段。Turk在1991年[6]提出PCA方法,主要通过将训练人脸图片投影到特征子空间中产生若干特征脸,以达到降维的目的。虽然PCA方法简单有效,但传统PCA需要将一个图像矩阵转化为一个高维[7],另外传统PCA在特征提取过程中对图像每个像素是平等对待的,未考虑人脸不同区域对识别贡献不同。Yang在2004年提出二维主成分分析法(2DPCA)[8],其直接利用图像矩阵构造散布阵,回避了维数灾难问题,大幅降低了特征提取的计算量。在 2DPCA基础上,ZHANG等[9]提出双向PCA(BD-PCA)算法,将行和列上的 PCA组合在一起,避免了2DPCA存在的信息缺失现象。据此,本文提出加权的双向PCA(BD-WPCA)算法,在图像预处理阶段,用双中心羽化加权以加强人脸主要器官的权值;在特征提取时采用BD-PCA分别在行和列上进行双边降维。在VS2010环境下的实验表明,提出的算法能在减小计算量的同时获得更高的识别正确率。
1 图像加权原理及方法
由于传统PCA在特征提取过程中对每个像素点是平等对待的,而在人脸识别中不同面部特征对识别的贡献不同。根据经验,人眼、鼻子、嘴巴区域在人脸识别中处于主要地位,而额头、下颚等平滑区域处于相对次要地位。因此,本文在图像预处理时提出双中心羽化加权方法,通过调节参数,提高特征提取时人脸主要器官的权值。
1.1 羽化加权函数
对图像加权,最重要的是选择恰当的加权函数。羽化函数是一个高斯分布函数,能对人脸的各维特征加权,它的表达式为:
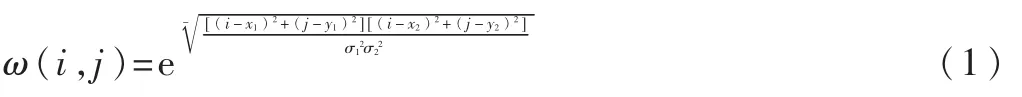
其中 (i,j)表示像素点的位置,(x1,y1)和(x2,y2)分别是两个羽化中心的位置,σ1和σ2用来控制函数的形状和大小,通过调节σ1和 σ2可以构成类椭圆形以更好地拟合人脸。
在 92×112 的图片范围内,取 (x1,y1)和 (x2,y2)分 别为(46,45)和(46,80),σ1=σ2=10 的羽化效果如图2 所示,取 (x1,y1) 和 (x2,y2) 分 别 为 (46,45)和 (46,80),σ1=σ2=15的羽化效果如图3所示。可见,双中心羽化函数是一个双高斯分布的函数,呈现为中心高亮,外围减暗的圆圈。在人脸图像加权的实际应用中,应调节参数使加权中心在面部特征明显的区域,并调节σ1和 σ2使函数形状大小适宜,吻合脸部,以增加眼睛嘴巴三角区的权值。
1.2 人脸图片加权预处理

图2 (46,45),(46,80),σ1=σ2=10时的羽化效果

图3 (46,45),(46,80),σ1=σ2=15时的羽化效果
在人脸识别中,本文将两个加权点设置在眉心和嘴巴中心的位置(由人脸检测阶段测出),并设 σ1=σ2=30。加权效果如图4所示。

图4 加权效果
可见,加权处理过后的人脸图片,突出了眼睛、鼻子、嘴巴主要器官组成的三角区域,降低了额头、下颚等处于次要地位特征的权值。
2 基于双中心加权和双向PCA的人脸识别
传统的PCA算法是基于一维向量的,导致图像的二维结构遭到破坏且易造成维数灾难。因此,本文在图像加权后采用BD-PCA算法,保留图像二维结构的同时降低了特征提取耗时。
2.1 双向PCA基本原理
设训练样本中有 N个 m×n的图像样本 X1,X2,X3,…XN,其中第i个样本矩阵 Xi用m个 1×n的行向量表示,图像行方向上的总体散度阵可如下计算:
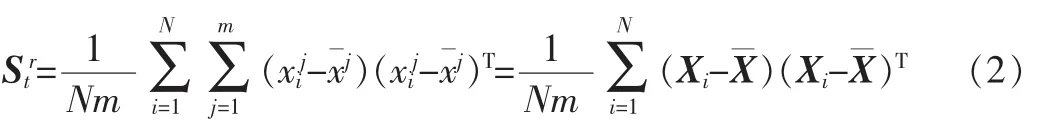
其中,xij为样本矩阵 Xi的第 j行为均值矩阵 X的第j行。行散度阵Str的前k个最大特征值对应的特征向量组成的矩阵就是行映射阵:

其中,ωir表示 Str的第i个最大特征值对应的特征向量。
同理可求出列方向上的总体散度阵以及列映射阵:
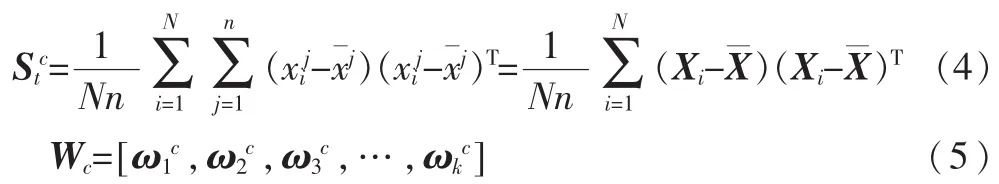
其中,xij为样本矩阵Xi的第 j列为均值矩阵 X的第 j列。ωic表示Stc的第i个最大特征值对应的特征向量。
求出Wr与Wc后,便可求出图像X的特征矩阵:

2.2 基于BD-WPCA的人脸识别算法
基于BD-WPCA的人脸识别具体实现方法如下:
(1)对训练样本和待测样本进行双中心羽化加权处理。
(2)将训练样本和待测样本用式(2)、(3)求出行映射阵Wr。
(3)将训练样本和待测样本用式(4)、(5)求出列映射阵 Wc。
(4)根据式(6)求出每个样本的特征矩阵 Y,并转换为行向量y。
(5)求出待测样本向量与训练样本向量之间的欧氏距离并用K近邻法[10]分类,实现人脸识别。
3 实验结果与分析
本文在VS2010环境下编写原型系统,在Intel Core i5-4200 2.5 GHz CPU、8 GB内存的 Win8系统笔记本上,针对传统PCA、双中心羽化加权 PCA、双向 PCA和本文方法分别进行实验。
实验样本由自行采集的20个加ORL人脸库中的40个人共60个人,600张人脸图片构成。采集样本时,先将RGB空间彩色图转换为灰度图,再调用OpenCV库中的函数cvResize()来实现双线性插值缩放。每幅图片归一化为112×92,256级灰度图。实验前,为补偿光照影响,先将人脸灰度图像进行直方图均衡化处理。部分样本如图5所示。

图5 部分人脸库样本
实验时,每次挑选一人进行实验,以识别率作为判定准则,识别率设定为正确识别数除以总实验次数。对四种方法分别进行实验,K近邻分类时取k=4,实验结果如表1所示。
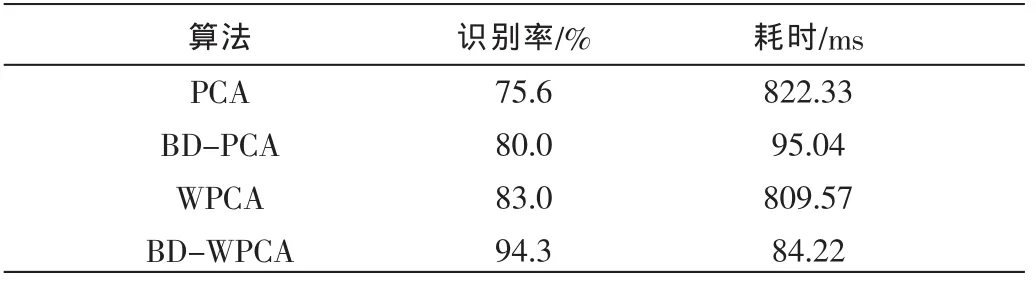
表1 实验结果
可见,双向PCA在一维PCA基础上极大地提升了计算速度,传统PCA耗时822.33 ms,而BD-PCA只需要95.04 ms,耗时缩短89%,这是因为在特征提取时,BD-PCA较于传统PCA用图像矩阵来计算协方差矩阵,维数远小于传统PCA中由图像转化的一维矩阵。此外,BD-PCA综合考虑了图像的行和列,特征选取更为合理,所以识别率也有所提高。比较WPCA与传统PCA可知,加权处理后将识别率从75.6%提升至83.0%,虽然对计算量影响甚微,但通过改变图像不同像素点的权重,使特征选择更利于分类。从表1可看出,本文所使用的BD-WPCA在传统PCA基础上,使识别率提高了18.7%,且耗时降低90%。提高识别精度的同时大大缩短计算耗时,且比单独使用BD-PCA或WPCA都有性能提高,这是因为BD-WPCA在识别前通过双中心羽化加权提高了人脸主要器官的权值,且根据二维图像矩阵的双向PCA降维,综合了两者优势。
4 结束语
针对传统PCA方法在人脸识别应用中的缺陷,本文提出了一种基于双中心羽化加权和双向PCA的人脸识别方法,该方法在识别前对图像进行双中心羽化加权处理,识别时用双向PCA降维。实验表明,与传统PCA和其他方法相比,本文方法获得了较高的识别率,且时间复杂度较小。但是,本算法对光照的鲁棒性不强,且在人脸细节出现变化如做表情、戴眼镜等情况时会有误差产生,这将是下一步研究工作的重点。
[1]唐亮.面向人脸识别的子空间分析和分类方法研究[D].杭州:浙江大学,2009.
[2]BRUNELL R,POGGIO T.Face recognition:features versus templates[J].IEEE Transactions Pattern analysis and Machine Intelligence,1993,15(10):1042-1052.
[3]ROUDEY H A,BALUJA S,KANADE T.Neural networkbased face detection[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1998,20(1):23-40.
[4]余龙华,王宏,钟洪声.基于隐马尔科夫模型的人脸识别[J].计算机技术与发展,2012,22(2):25-28.
[5]JAIN A K,DUIN R P W,MAO J.Statistical pattern recognition:a review[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(1):4-37.
[6]TURK M,PENTLAND A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.
[7]曾岳.人脸识别方法研究[D].西安:西安电子科技大学,2011.
[8]Yang Jian,Zhang David,Yang Jingyu.Two-dimensional PCA:a new approach to appearance-based face representation and recognition [J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2004,26(1)131-137.
[9]Zuo Wangmeng,ZHANG David.Bidirectional PCA with assembled matrix distance metric for image recognition[J].IEEE Transaction on Machine Intelligence,2006,36 (4):863-872.
[10]边肇棋,张学工.模式识别(第 2版)[M].北京:清华大学出版社,2000.

