考虑DG与网架适应性的配网双层优化规划

芦新波，张建华，行晋源（华北电力大学电气与电子工程学院，北京102206）

考虑DG与网架适应性的配网双层优化规划

芦新波，张建华，行晋源
（华北电力大学电气与电子工程学院，北京102206）

为了适应高渗透率分布式发电并网及主动管理的配网发展趋势，在考虑分布式发电与网架适应性的情况下，建立了以年社会成本最小为目标的配网双层优化规划静态经济模型。上层模型是以系统年综合费用最小为目标的配网网架规划，下层模型是以年投资运行费用最小为目标的分布式电源选址定容规划。并根据各自的特点，分别采用二进制顺序编码的改进自适应单亲遗传算法和十进制顺序编码的改进粒子群算法求解。以某实际规划区域作为算例，验证所提模型的合理性和有效性。

配网网架规划；分布式电源；选址定容；双层优化规划；单亲遗传算法；粒子群算法

在当前电力需求持续增长、传统能源短缺和环境污染的背景下，分布式发电（distributed generation，DG）凭借其运行方式灵活、环境友好等优点备受青睐[1-3]。由于DG渗透率不断增高的影响，配网不确定性和复杂性大大增加[4-7]，使得进行网架规划时必须考虑DG并网位置与容量。此外，一方面，传统配网网架规划方法仅仅确定一定规划目标下的线路建设方案，无法适应大量DG并网的发展趋势；另一方面，现代智能配电网要求能够主动管理DG、电动汽车、微网等新型电力用户[8-10]，充分发挥它们在节能降损、减少污染、提高供电可靠性与改善电能质量等方面的积极作用，促使系统的综合性能更优。因此，在高渗透率DG并网情况下，有必要将DG选址定容和网架建设联合考虑，采用新的科学方法进行协调规划，形成更优的配网建设方案，增强对新型电力用户的适应性，保障并增强系统经济性、安全性、可靠性和灵活性。

目前含DG的配网规划研究已有一定的进展。文献[11]建立了考虑主动管理的配网双层规划模型，并采用单亲遗传算法和原对偶内点法求解；文献[12]考虑DG的最大供电范围，根据功率圆，提出了DG的优化配置方法；文献[13-14]在分析DG对网损和可靠性等影响基础上，计及DG出力随机性，建立了配网网架柔性规划模型。但在这些研究中，均在提前设定DG并网容量及位置的条件下，侧重对网架结构进行优化规划，从本质上人为割裂了DG与电网之间的天然内在联系，忽略了二者的交互影响，因此最终规划方案很难保证具有全局最优性。文献[15]考虑分布式电源调度运行的影响，建立了配网网架的优化重构模型；文献[16]根据新增负荷总量确定待建DG容量，建立了配网网架扩展规划的多智能体遗传模型；文献[17]考虑DG出力不确定性，提出了配网网架重构的规划方法。但文献[15-17]均只侧重配网网架优化规划，未考虑DG对原有网架结构的影响，具有一定局限性。

基于此，本文从将DG和网架结构整体协调规划的角度出发，考虑DG与网架的适应性，建立了配网静态双层优化规划经济模型，上层为网架规划子问题，下层为DG选址定容子问题。针对模型特点，分别采用改进的自适应单亲遗传算法和改进的粒子群算法求解，最后利用某实际规划区域作为算例验证模型与算法的有效性。

1　DG与网架适应性配网规划模型

DG与网架适应性配网联合规划既涉及网架规划，又涉及DG选址定容，假若将二者统一编码与求解，将大大增加模型决策变量维度，尤其针对大规模系统时，将使计算规模变得难以承受。此外，联合规划问题具有天然的分解性，网架规划为DG选址定容提供网络拓补方案，后者又为前者提供DG配置方案，故可将二者分解成2个相对独立的子问题，针对各自特点，分别选择合适、优秀的目标函数与约束条件及稳定的求解算法，从而保障有效获取最优的规划方案[18]。因此，本文根据分解协调思想，将联合规划问题转化为双层规划模型，上层为以网络年综合费用最小为目标的配网网架规划模型，解决线路建设问题；下层为以年综合运行费用最小为目标的DG选址定容模型，在上层规划所得网架下确定最优的DG并网位置与容量。

1.1上层规划模型

1.1.1目标函数

上层模型为以系统年综合费用最小为目标的配网网架规划，其目标函数表达式为[19]

式中：Cup为网络年综合费用，万元；Cline为网架投资及运行费用等年值，万元；Closs为系统年损耗费用，万元。Cline、Closs计算公式见式（2）—式（3）。

式中：ΩL为拟选建线路总集合；C1i=γi+αi，γi为投资回报率；αi为设备折旧维修费用率；Ti为支路i的总投资费用，对于已建设线路仅计及运行费用，万元；Ce为单位电价，元/kW·h；τmax为最大负荷损耗小时数；ΔPi为支路i有功损耗，kW；

1.1.2约束条件

综合考虑配网网架规划和系统运行的实际情况，上层模型包含以下约束条件：

1）辐射状连通性网络约束如式（4）所示，其中：m为系统支路总数；n为节点总数；且要求网络中不能存在孤点、孤链、孤环。

2）功率平衡约束如式（5）所示，其中：A为节点关联矩阵；C为网络潮流分布矩阵；D为负荷需求矩阵。

3）可靠性约束如式（6）所示，本文用系统供电量不足量ET来表征其可靠性水平，ETmax为系统可以容忍的供电不足量最大值[20]，kW·h。

ET计算公式如式（7）所示，其中：fTj为第j条线路的年平均故障率；PTij为第j条线路发生故障时节点i处的供电不足功率，kW，若该节点有DG接入，则应减去DG的供电功率。

4）节点电压约束如式（8）所示，其中：Uimax和Uimin分别为节点i电压Ui的上限和下限；KU为节点电压越限惩罚因子，作为对偏离运行极值的惩罚，一般取值较大，满足要求时为0。

5）线路载流量约束如下式，其中：Ij为支路j的电流；Ijmax为支路j允许通过的电流上限；KI为支路电流越限惩罚因子，取值原则同KU。

将节点电压和线路载流量约束以惩罚因子的形式并入归一化目标函数，得新的上层目标函数：

1.2下层规划模型

1.2.1目标函数

下层模型为以年综合运行费用最小为目标的DG选址定容规划，其目标函数表达式为

式中：CF为DG的安装投资费用等年值，万元；COM为DG年运行维护费用，万元；Cen为向上级电网的购电成本，万元；CH为政府鼓励新能源类型DG发电而给予的政策性补贴，万元。CF、COM、Cen、CH的计算公式为

式中：ΩDG为接入配网的DG总集合；CfDG为DG单位容量安装成本，元/kW；SDGi为第i个DG的安装容量，kW；r为贴现率，取为10%；nDG为DG投资回收期，一般取10 a；Tmax为DG年最大发电小时数；ComDG为DG单位电量运行维护费用，元/kW·h；λDG为DG的功率因数；ΔPi为支路i有功损耗，kW；PLi为节点i的负荷功率，kW；ChDG为DG单位电量的补贴费用，元/kW·h。

1.2.2约束条件

下层模型约束条件包括如式（5）—式（9）所示的功率平衡约束、可靠性约束、节点电压约束、线路载流量约束，此外，还有以下约束：

1）待选节点DG安装容量约束如式（16）所示，其中，SDGimax为节点i允许接入的DG最大容量。

2）DG总安装容量约束如式（17）所示[21]，其中，S∑DG为DG入网总容量；SL为电网负荷总容量的35%；K∑DG为DG并网容量惩罚因子，取值原则同KU。

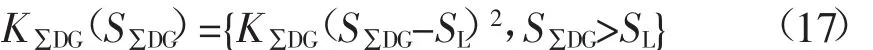
将节点电压约束、线路载流量和DG总安装容量约束以惩罚因子的形式并入归一化目标函数，所得新的下层规划目标函数为

1.3配网双层规划总模型

考虑DG与网架适应性的配网双层优化规划总模型以年社会成本最小为目标，函数表达式为

其总模型示意图如图1所示，上层是配网网架规划子问题，下层是DG选址定容子问题。上层规划将网架建设方案作为参数传递给下层，下层模型在上层网架的基础上对DG进行选址定容规划，并将其决策方案传递给上层，上层模型利用下层传递上来的DG位置、容量对网架结构优化规划……，这样上、下层模型反复迭代优化规划，直至最后输出DG选址定容与网架建设综合最优的配网建设方案。

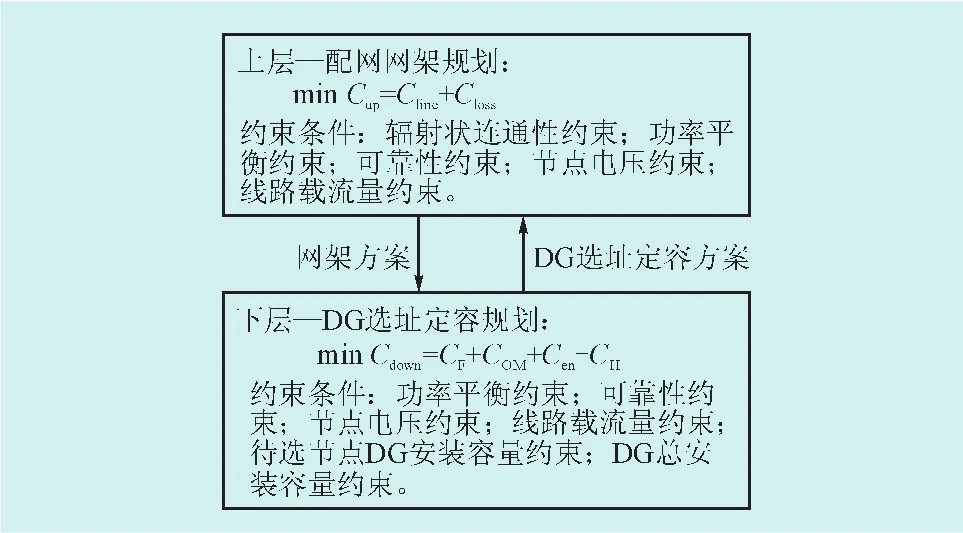
图1　配网双层规划模型Fig.1Distribution network bi-level programming model

2　双层规划模型求解方法

2.1上层模型求解

上层模型是配网网架规划问题，根据其特点，本文采用改进的自适应单亲遗传算法（adaptive partheno-genetic algorithm，APGA）求解。APGA与常规遗传算法（genetic algorithm，GA）相似，也是一种随机并行搜索求解算法，基本原理：仿效自然界进化法则，对实际问题编码，形成种群，以迭代方式利用相应算子进行遗传操作，种群逐代进化，最终实现问题求解[22]。但与GA不同，APGA利用基因重组算子（包括基因换位、移位、倒位等算子）进行遗传操作，代替GA中交叉算子的功能。为解决算法收敛速度慢、可能早熟等问题，本文采用自适应策略和精英保持策略改进其收敛性能。

2.1.1基因编码与初始种群生成

考虑网架规划问题特点，结合APGA算法，采用二进制的顺序编码方式。对应位置基因若为“0”，则该线路不建，否则反之。如此，n条待建线路的建设方案，可以用长度为n的染色体表示，这样可大大简化算法编码与解码工作，提高算法运行效率。此外，由于配网网架具有辐射状、连通性约束，求解过程中会产生不可行解，可采用适当方法[23]，判断并修复不可行解，提高算法迭代效率，节省计算时间；另外，采用最小生成树算法产生初始种群[24]，解决随机生成初始种群形成不可行解问题。

2.1.2上层规划模型求解流程

基于改进APGA的上层模型求解流程如下：

1）输入网架规划所需原始数据。

2）对决策变量进行二进制顺序编码，设置APGA运行参数。

3）利用最小树生成算法生成初始种群。

4）利用前推回代方法进行潮流计算，对于不满足约束条件个体加罚函数，计算各个体目标函数值及其对应适应度值。

5）进行选择、基因重组、变异等遗传操作，修复不可行解，产生子代种群。

6）对新种群进行潮流计算及对不满足约束条件个体加罚函数，计算各个体目标函数值及其对应适应度值。

7）根据精英保持策略，选取少量优秀个体代替子代较差个体。

8）判断是否满足迭代终止条件，是则计算结束返回结果，否则从步骤5）迭代继续。

2.2下层规划模型求解

粒子群算法（particle swarm optimization，PSO）是一种群体智能优化算法，仿效鸟类捕食行为，每个粒子代表问题潜在解，对应一个适应度值，粒子速度决定移动方向与距离，而速度根据粒子自身及种群移动经验动态调整，最终实现问题求解[25]。迭代过程中，各粒子据下式更新速度与位置

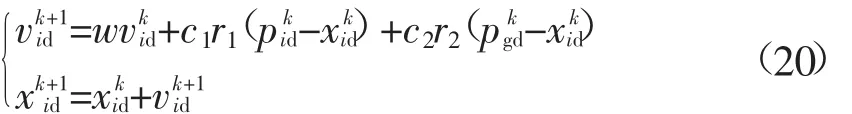
PSO算法具有较快的收敛速度，但是容易陷入局部解，本文采用逐步减小的时变权重与异步时变的学习因子相配合的方法，改善其收敛性能。根据式（21）分别动态调整w、c1、c2：

式中：wmax、wmin为w最大与最小值；c1i和c2i、c1f和c2f分别为c1、c2初始值与终值；niter、niter_max分别为当前与最大迭代次数。这样使算法在迭代初期有较好全局搜索能力，后期有精确局部搜索能力。

2.2.1编码方案与适应度函数

考虑DG选址定容问题的特点，结合PSO算法，下层模型求解采用十进制的顺序编码方式。设配网mDG个节点允许接入DG，则DG安装方案可用一组向量X=（x1，…，xmDG}表示，xi对应为节点i的DG建设情况，若xi=0则该节点不安装DG，否则该节点待建DG，且安装容量为PDGi=PSxi，其中PS为DG基准安装容量。另外，本文直接选取式（19）所示归一化下层目标函数作为算法求解适应度函数。

2.2.2下层规划模型求解流程

基于改进PSO的下层模型求解流程：

1）输入DG选址定容规划所需原始数据。

2）对决策变量进行十进制顺序编码，设置PSO运行参数，随机形成初始种群。

3）利用前推回代方法进行潮流计算，对于不满足约束条件粒子加罚函数，计算其归一化目标函数值及对应适应度值。

4）设置粒子个体极值及群体极值，并根据公式（20）更新惯性权重和学习因子，计算粒子速度及位置，形成新的种群。

5）对新种群计算其归一化目标函数值及其对应适应度值，更新粒子个体极值及群体极值。

6）判断是否满足迭代终止条件，是则计算结束返回结果，否则从步骤4）迭代继续。

2.3总模型求解流程

本文采用二进制顺序编码的改进自适应单亲遗传算法，和十进制顺序编码的改进粒子群算法，对考虑DG与网架适应性的配网双层优化规划模型求解，其总模型求解流程如图2所示。

3　算例及结果

本文采用某29节点实际规划区域作为算例，规划电压等级为10 kV，年限为20年。经过前期负荷预测、电力电量平衡、电气计算等校验与综合分析，规划区域节点与拟建线路编号及关联关系见图2、图3；节点负荷见表1；选用LGJ-120/20架空线，线路参数见表2，拟建线路长度与编号见表3；节点3、7、9、12、14、17、18、19、20、23拟接入DG。

图2　配网双层规划求解流程Fig.2Distribution network bi-level programming solving process

图3　节点与拟建线路关联图Fig.3Nodes associated with proposed circuit diagram

表1　节点负荷数据Tab.1Node load data

表2　LGJ-120/20型线路参数Tab.2LGJ-120/20 circuit parameters

表3　拟建线路长度Tab.3The proposed line lengthkm

其他相关参数如下：线路投资回收率0.08，折旧维修率0.04；单位电价0.5元/kW·h；最大负荷损耗小时数3 200；越限惩罚因子为1 000；DG单位容量安装成本2 800元/kW，运行维护费用0.20元/kW·h，补贴费用0.15元/kW·h，最大发电小时数1 700，功率因数0.9，安装基准容量25 kW。

利用本文介绍的配网双层优化模型及求解算法，求解算例，设为方案1，网架规划结果如下。

为了进行对比分析，验证双层规划模型的有效性，本文又根据相同的参数设置，按照常规的分阶段配网规划（先网架规划，后DG选址定容）及不考虑DG的网架规划方法进行优化规划，设分别对应为方案2、3。常规方法规划网架时也未考虑DG并网对配网负荷预测、潮流分布等的影响[26-28]，故方案2、方案3最优网架规划结果相同。考虑适应性的最优网架建设方案见图4。不考虑DG的最优网架建设方案见图5。

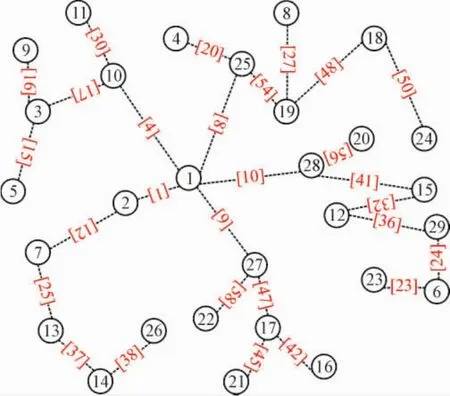
图4　考虑适应性的最优网架建设方案Fig.4The optimal network frame construction plan considering adaptive

图5　不考虑DG的最优网架建设方案Fig.5The optimal network frame construction scheme regardless of DG

方案1、2中DG的安装位置与容量如表4所示，3种规划方案的相关费用计算结果如表5所示。

表4　方案1与2中DG安装位置及容量Tab.4Scheme 1 and 2 DG installation location and capacity

表5　3种规划方案各相关费用Tab.5The relevant expenses of three scheme

分析表5数据得，方案1、2中网络损耗、购电成本及社会总成本费用均小于方案3，而且二方案网损下降率均达到20%以上，此外方案1的网架投资费用也小于方案3；由此可见，DG接入可有效改善系统运行并带来可观的经济效益。又由表4数据可知，方案1、2中DG安装总容量虽然相同，但是其具体安装位置及相应容量并不相同，由表5可知方案1中网架投资、网络损耗及社会总成本均小于方案2；由此可见，方案1比方案2经济效益更好，DG与配网网架建设方案更加合理，二者兼容性更好，DG对延缓线路投资及减小系统损耗等的积极影响效果更明显，故其网架投资、系统总损耗及社会总成本也更小。综上可知，双层优化规划模型更有利于发挥DG对配网的积极作用，提高系统对清洁能源接纳和对大规模DG并网的兼容与适应能力。

4　结论

本文在考虑分布式发电与网架适应性的基础上，建立了配网双层优化规划模型，提出分别采用二进制顺序编码的改进自适应单亲遗传算法与十进制顺序编码的改进粒子群算法对上、下层模型求解，并通过计算相应算例验证了模型的正确及有效性。最后得出以下结论：

1）DG接入配网可以使系统运行更加高效、环保，并能带来可观的经济效益，更符合我国节能减排和开发新能源的战略要求。

2）配网双层优化规划模型在网架规划时考虑了DG并网对负荷预测、潮流分布、网络损耗、电能质量等的影响，同时也考虑了网架建设与DG选址定容之间相互制约与影响的关系，使得DG并网位置与容量、网架结构更加合理且经济效益更好，更能有效发挥DG在改善系统运行等方面的积极作用，提高系统对清洁能源接纳能力，促进DG发展。

3）考虑DG与网架适应性的配网双层优化规划方法可以更好地反映未来大规模DG接入配网的特点，更有利于实现配网主动管理的要求，更符合未来智能配电网的发展趋势，并为以后考虑DG、微网、电动汽车换电站等新型电源与负荷的配网规划工作提供有益的理论参考。

[1]DJAPICP，RAMSAYC，PUDJIANTOD，et al．Taking an active approach[J]．IEEE Power and Energy Magazine，2007，5（4）：68-77．

[2]武星，殷晓刚，宋昕．中国微电网技术研究及其应用现状[J]．高电压电器，2013，49（9）：142-149．WU Xing，YIN Xiaogang，SONG Xin．Chinese micro grid technology research and application status[J]．High Voltage Apparatus，2013，49（9）：142-149（in Chinese）．

[3]THOMAS A，G觟RAN A，LENNART S．Distributed generation：a definition[J]．Electric Power System Research，2001，57（3）：195-204．

[4]雷金勇，李战鹰，卢泽汉．分布式发电技术及其对电力系统影响研究综述[J]．南方电网技术，2011，5（4）：46-50．LEI Jinyong，LI Zhanying，LU Zehan．Review on the research of distributed generation technology and its impacts on electric power systems[J]．Southern Power System Technology，2011，5（4）：46-50（in Chinese）．

[5]CARMEN L T B，VINICIUS F M．Multistage expansion planning for active distribution networks under demand and distributed generation uncertainties[J]．Electrical Power and Energy Systems，2012，36（1）：107-116．

[6]胡海安，张纳川，陈兆骅．分布式电源并网对电网运行和管理制度的影响及其思考[J]．电力与能源，2013，34（6）：661-668．HU Haian，ZHANG Nachuan，CHEN Zaohua．The impact and thinking of distributed generation on operation and management of grid[J]．Electric Power and Energy，2013，34（6）：661-668（in Chinese）．

[7]BRAHMA S M，GIRGIS A A．Development of adaptive protection scheme for distribution systems with high penetration of distributed generation[J]．IEEE Trans on Power Delivery，2004，19（1）：56-63．

[8]OCHOA L F，DENT C J，HARRISON G P．Distribution network capacity assessment:variable DG and active networks[J]．IEEE Transaction on Power Systems，2010，25（1）：87-95．

[9]张节潭，程浩忠，姚良忠．主动管理在含有分布式电源的配电网中的应用[J]．电力科学与技术学报，2008，23（1）：18-22．ZHANG Jietan，CHENG Haozhong，YAO Liangzhong．Application of active management to distribution network with DG[J]．Journal of Electrical Power Science and Technology，2008，23（1）：18-22（in Chinese）．

[10]尤毅，刘东，于文鹏．主动配电网技术及其进展[J]．电力系统自动化，2012，36（18）：10-16．YOU Yi，LIU Dong，YU Wenpeng．Technology and progress of active distribution network[J]．Automation of Electric Power Systems，2012，36（18）：10-16（in Chinese）．

[11]方陈，张翔，程浩忠．主动管理模式下的含分布式发电的配电网网架规划[J]．电网技术，2014，38（4）：823-829．FANG Chen，ZHANG Xiang，CHENG Haozhong．Framework planning of distribution network containing distributed generation considering active management[J]．Power System Technology，2014，38（4）：823-829（in Chinese）．

[12]王海涛，史吏，任建文．基于功率圆的分布式电源优化配置研究[J]．电力科学与工程，2012，28（10）：28-32．WANG Haitao，SI li，REN Jianwen．The optimal allocation of distributed generation based on power circle[J]．Electric Power Science and Engineering，2012，28（10）：28-32（in Chinese）．

[13]凡鹏飞，张粒子，熊浩清．基于改进BCC算法的含微电网的配电网网架规划[J]．电力系统保护与控制，2012，40（10）：12-18．FAN Pengfei，ZHANG Lizi，XIONG Haoqing．Distribution network planning containing micro-grid based on improved bacterial colony chemotaxis algorithm[J]．Power System Protection and Control，2012，40（10）：12-18（in Chinese）．

[14]李志铿，王钢，陈志刚．计及区域自组网的含分布式电源配电网网架柔性规划[J]．电力系统保护与控制，2013，37（6）：42-47．LI Zhikeng，WANG Gang，CHEN Zhigang．Meter and the area of ad-hoc network distributed power distribution network frame of flexible planning[J]．Power System Protection and Control，2013，37（6）：42-47（in Chinese）．

[15]庄园，贺海，杨晓慧．含分布式电源优化调度的配电网络重构[J]．电网与清洁能源，2012，28（11）：13-18．ZHUANG Yuan，HE Hai，YANG Xiaohui．Distribution network reconfiguration with optimal allocation of distri-buted generation[J]．Power System and Clean Energy，2012，28（11）：13-18（in Chinese）．

[16]徐玉琴，李雪冬，张继刚．考虑分布式发电的配电网规划问题的研究[J]．电力系统保护与控制，2011，39（1）：87-93．XU Yuqin，LI Xuedong，ZHANG Jigang．Research on distribution network planning considering DGs[J]．Power System Protection and Control，2011，39（1）：87-93（in Chinese）．

[17]魏辉，曾令全．含分布式电源的配电网络重构[J]．华北电力大学学报，2012，39（2）：23-27．WEI Hui，ZENG Lingquan．The reconfiguration of distribution network with distributed generation[J]．Journal of North China Electric Power University，2012，39（2）：23-27（in Chinese）．

[18]程浩忠，张焰，严正．电力系统规划[M]．北京：中国电力出版社，2014．

[19]李伟伦，桂淑华，孙志刚．考虑分布式电源的配电网优化规划[J]．江苏电机工程，2010，29（5）：30-36．LI Weilun，GUI Shuhua，SUN Zhigang．Considering distributed generation distribution network optimal planning[J]．Jiangsu Electrical Engineering，2010，29（5）：30-36（in Chinese）．

[20]郭贤．分布式电源及典型微网的规划方法研究[D]．上海：上海交通大学，2013．

[21]叶德意，何正友，臧天磊．基于自适应变异粒子群算法的分布式电源选址与容量确定[J]．电网技术，2011，35（6）：155-160．YE Deyi，HE Zhengyou，ZANG Tianlei．Siting and sizing of distributed generation planning based on adaptive mutation particle swarm optimization algorithm[J]．Power System Technology，2011，35（6）：155-160（in Chinese）．

[22]王爱霞，王思华，王明．基于粒子群算法的变电站接地网优化研究[J]．电瓷霹雷器，2013（3）：100-104．WANG Aixia，WANG Sihua，WANG Ming．Optimization research of grounding grid for substations based on the particle swarm algorithm[J]．Insulators and Surge Arresters，2013（3）：100-104（in Chinese）．

[23]徐玉琴，李雪冬．基于改进免疫克隆选择算法的含分布式电源配电网规划方法[J]．电网技术，2010，34（8）：97-102．XU Yuqin，LI Xuedong．An improved immune clonal selection algorithm based planning method for distribution networkwithdistributedgenerators[J]．PowerSystem Technology，2010，34（8）：97-102（in Chinese）．

[24]张艳．基于改进最小生成树算法的油田网架优化研究[D]．大庆：东北石油大学，2011．

[25]史峰，王辉，郁磊．MATLAB智能算法30个案例分析[M]．北京：北京航空航天大学出版社，2011．

[26]刘刚，陈荣锋，莫芸，等.10 kV架空配电线路避雷线架设高度的探讨[J].电瓷避雷器，2012，135（4）:33-38. LIU Gang，CHEN Rongfeng，MO Yun，et al.Discussion on the erecting height of ground wire in 10 kV overhead distribution lines[J].Insulators and Surge Arresters，2012，135（4）:33-38（in Chinese）．

[27]刘金亮，杨彩梅，林国华，等.架空配电线路感应雷过电压仿真分析[J].电瓷避雷器，2012，135（4）:43-48. LIU Jinliang，YANG Caimei，LIN Guohua.Simulation and analysis on lightning induced overvoltage of overhead distribution lines[J].Insulators and Surge Arresters，2012，135（4）:43-48（in Chinese）．

[28]向军，周羽生，郑剑武，等.1 000 kV交流紧凑型输电变电站雷击侵入波分析[J].电瓷避雷器，2012（3）:67-70. XIANG Jun，ZHOUYusheng，ZHENG Jianwu，et al. Analysis on lightning invasion waves of 1 000 kV AC compacttransmission substation[J].Insulators and Surge Arresters，2012（3）:67-70（in Chinese）．

（编辑董小兵）

Bi-Level Optimization Planning of Distribution Network Considering Adaptability between DG and Framework

LU Xinbo，ZHANG Jianhua，XING Jinyuan
（School of Electrical and Electronic Engineering，North China Electric Power University，Beijing 102206，China）

In order to adapt to the distribution network development trend of high permeability of DG interconnection and active management，considering adaptability between DG and the framework this paper establishes an optimal planning economic bi-layer model of the distribution network with target of minimizing social cost.The upper model is a distribution network frame-work planning with the goal of minimizing comprehensive cost，while the lower model is a planning of DG siting and sizing based on yearly operation cost minimum as the goal.According to their characteristics，this paper adopts the improved adaptive partheno-genetic algorithm of binary sequence coding and the improved particle swarm optimization of decimal sequence coding for solution.Finally，the paper uses the actual planning area as an example to verify the rationality and validity of the proposed model.

distribution network framework planning；DG；siting and sizing planning；Bi-level optimization planning；adaptive partheno-genetic algorithm；particle swarm optimization

1674-3814（2015）06-0056-08

TM711

A

国家自然科学基金（51277067）。

ProjectSupportedbyNationalNatureScienceFoundation（51277067）.

2014-01-16。

芦新波（1989—），男，硕士研究生，研究方向为电力系统规划等；

张建华（1952—），男，教授，博士生导师，研究方向为电网规划、电力系统风险评估等；

行晋源（1990—），男，硕士研究生，研究方向为分布式电源并网与控制技术等。