改进的菌群趋药性算法优化PID控制参数①

杨　凡， 黄永青，2， 宋洪儒（.铜陵学院信息技术与工程管理研究所，安徽 铜陵 244000；2.合肥工业大学管理学院，安徽 合肥 20009；.铜陵学院电气工程学院，安徽 铜陵 244000）

改进的菌群趋药性算法优化PID控制参数①

杨凡1， 黄永青1，2， 宋洪儒3
（1.铜陵学院信息技术与工程管理研究所，安徽 铜陵 244000；2.合肥工业大学管理学院，安徽 合肥 230009；3.铜陵学院电气工程学院，安徽 铜陵 244000）

提出改进的细菌群体趋药性算法（BCC）来优化PID参数.针对BCC算法在多维变量搜索时，耗时且难于收敛到最优值，提出2种改变，一为变步长搜索，二为每一个细菌变量设定活动区域，移动后如超出设定区域，将采用区域内的固定值取代或精英取代两种方式优化，通过PID控制参数进行仿真实验，表明改进后的算法在参数的精度、稳定性和优化时间上都有很好的表现.

PID控制器；细菌群体趋药性算法；变步长搜索；精英取代

文章编号：1008-1402（2015）06-0877-03

0　引言

在控制工程中，PID控制具有结构简单、鲁棒性强、易于工程实现等特点，在工业控制过程中得到了广泛的应用.然而在此过程中，多数控制对象是非线性的，使用传统的控制方法难以实现对参数的优化整定，易产生振荡和大的超调.因此，PID控制器的3个参数Kp、Ki和Kd的选取，对控制系统的性能具有重要影响，解决其参数的整定也成为应用PID控制器的关键技术［1］.

细菌群体趋药性（Bacterial Colony Chemotaxis，BCC）算法是浙江大学的李威武等人［2］在细菌趋药性（Bacterial Chemotaxis，BC）算法的基础上，融入群体智能的思想提出的，本文将根据PID参数的特点，提出一种改进的BCC算法，利用实验仿真来验证算法的有效性.

1　BCC优化算法

BCC算法是在单个细菌寻优的基础上，引入多个细菌通过交互信息的方式，择优获得最优点的群体智能算法，该算法常见的应用是对二维函数进行优化，进而可以扩展到对多维函数优化.该算法的步骤如下［2］：

（1）初始化算法的各个参数，如细菌个数、范围和维数，初始和终止收敛精度，精度更新常数.依据公式确定系统参数T0，b，τc.

图1　BCC-E和BCC-D最优值的优化过程

（2）计算运动方向.以二维空间（xi，xi+1）为例，向左向右偏转的角度θi概率相同，均服从高斯概率分布.

（3）细菌运动距离l=v*τ，τ为移动时间.

τ的数值服从指数概率分布，由T决定：

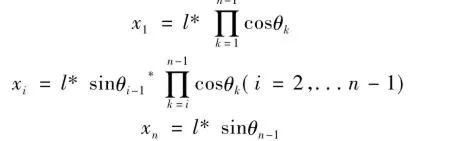
（5）确定第i个细菌在移动步数k时，周围拥有更好位置的其他细菌中心点位置，和向该中心点移动的距离，确定第i个细菌k+1移动步数的位置xi，k+1″（x1，…xn）；

（6）计算位置xi，k+1'和xi，k+1″的函数值，取二者中较小的函数值对应的位置，作为细菌i在第k +1步的移动位置；

（7）重复步骤4～6，直至中止条件满足.

算法中各个细菌的移动速度不变，当连续ne步前后函数绝对值的差小于一个欲先设定的小数，细菌将随机迁移一个新的位置.所有的参数采用全体更新策略.

2　BCC算法的改进

2.1精度下降梯度的改变

在BCC算法中，沿用的是全体参数自动更新策略，其中参数T0由公式（1）可知，ε是期望的计算精度，算法运行时需设置初始收敛εbegin和终止收敛精度εend，如当前精度满足时，会采用精度更新常数α得到一个新的精度εnew=εold/α，在算法初期，需要较大的下降梯度，在算法后期需较小的下降梯度，更利于寻优.由此采用下面的公式对α进行调整；其中αmin，αmax为α的下限和上限，gen为当前迭代代数，genmax为最大迭代次数.

随着进化代数的不同，α的值将发生变化；在算法初期时，α较小，下降梯度较大，即步长较大；后期时，α相对较大，步长变小.

2.2固定值或精英替代的细菌位置的引入

BCC算法中需先确定每一维变量范围，根据范围确定初始种群，在算法运行时，会出现一些细菌超出限定的范围.这时，一般采用将超出范围的每个细菌退回到上一次获得的位置，重新生成新的位置方法；但是，这种处理方式在处理多维变量问题时，特别耗时，结果令人不是很满意.由此提出2种改进方式，一种方式为，当生成的新的细菌位置x（x1…xn）中任何一维变量超出欲先设定的范围时，针对细菌不同维变量xi采用i维范围内的固定值取代，这个固定值可以是i维范围的上下限，并把使用这种取代策略的算法记为BCC-D；另一种方式为：精英取代，即记录上一代细菌群体中的最好细菌位置，当生成的第i个细菌新位置x（x1…xn）中任一维变量超出规定范围时，进行该位置的整体变量取代.同时对取代的细菌个数进行计数，如果个数超出总数的1/3，进行变异操作，保持种群的差异性，利于寻优，把使用这种取代策略的算法记为BCC-E.

3　改进的BCC算法优化函数实验

为了验证上述改进方法的有效性，利用下面的Sphere、Griewank两个测试函数，对改进的BCC算法（BCC-E）、PSO算法、GA算法进行优化比较.函数如下：

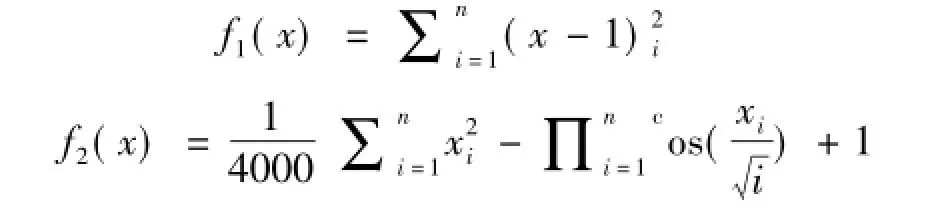
函数f1（x）∈［2，2］是单峰函数，只有一个全局最小点（1，1），函数值f1（x）=0；函数f2（x）∈［-2，2］是复杂多峰函数，全局最优值为0，在点（0，0）出获得.

三种算法的相关参数设置如下：BCC-E算法中细菌个数取20，初始精度设为10-2，终止收敛精度取10-6，精度下降梯度上限αmax为1.25，下限αmin为1.05，依据公式（4）得到每一代的α，变异概率Pm=0.6；PSO算法种群数取20，迭代数取1500Ga算法种群大小取200，终止代数1000，Pc=0.9，自适应变异操作.

测试函数维数为3，三种算法各运行100次，在时间、函数最优值精度和成功率上进行比较，见表1.由表可见，BCC-E算法用时较多，但函数最优值收敛精度较高.

表1　BCC-E，PSO，GA算法性能的比较

f1　1.473715　5.0e-013　100%　0.69976　9.2966e-008　100%　0.547367　1.9946e-007　100% f2　1.468537　1.11e-016　100%　0.788685　3.7324e-008　100%　0.585063　2.2151e-009　100%

4　 改进BCC算法优化PID参数仿真实验

在工业控制中，被控系统常被近似为一阶或二阶函数，本文被控对象采用的是二阶传递函数，输入对象为阶跃信号，采样时间为1ms.选用下式作为参数选取的最优指标：

式中，e（t）为系统误差，u（t）为控制器输出，tu为上升时间，w1，w2，w3为权值.

产生超调，采用惩罚功能，将最优量作为最优指标一项［15］.

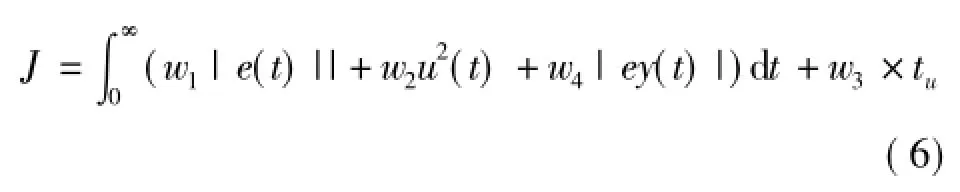
即最优指标J由三部分组成：第i代的误差error（i）的绝对值；第i代控制量输出u（i）；上升时间tu.

分别采用BCC-E和BCC-D方式对该二阶传递函数进行优化，优化的目标即为J.PID控制器有三个参数，算法变量维数即为三维；设定各参数取值范围Kp∈［0，20］、Ki和Kd∈［0，1］，则给出了两种算法中变量的初始化范围.两种算法除变量范围与第4节不同外，其他参数设置同上；公式（6）中设定w1=0.999，w2=0.001，w3=2.0，w4=100.两种方式获得的最优指标的优化过程见图1.

由图1可见，2种方式都用了较少的进化代数获得了最优值，BCC-E相比较BCC-D方式更能快速的获得最优，且最优值更小.通过多次优化仿真实验BCC-E获得的最优参数如下，最好适应值Bestf =24.0140；并且每次寻优操作结束后将有80%以上的细菌个体能够聚集在最优点；采用BCC-D方式获得的最优参数如下：Kp=19.7071，Ki=0. 2526，Kd=0.917，Bestf=24.1548；每次寻优操作仅有20%的细菌个体获得了最优值.

若采用BCC算法优化PID参数，该算法的各个参数如细菌个数、初始和终止精度与BCC-E参数设置相同，精度更新常数α为1.15，获得最优参数值及最优值为：Kp=60.3574，Ki=0.5047，Kd= 0.8337，Bestf=22.0552；与改进的两种BCC算法相比，BCC算法在进化时间和数值精度上没有太大的区别，但在优化指标J获得最优时，三个参数最终的取值将超出当初设定的范围，且大部分情况下各个参数取值不合常理.

为确保每个参数一直处于欲先设定的范围，针对PID参数的特点，提出BCC-D和BCC-E两种方式进行优化，每次优化结束后，所有的细菌都将处于预定范围，从获得的最优参数数据和优化时间可知，这2种改进方式是有效的、快速的.

［1］郭大庆，李晓，赵永进.基于改进PSO算法的PID参数自整定［J］.计算机工程，2007，38（18）：202-204.

［2］黄伟锋，林卫星，范怀科等.细菌觅食优化的智能PID控制［J］.计算机工程与应用，2011，47（21）：82-85.

Improved Bacterial Colony Chemotaxis Algorithm for the Optimization of PID Control Parameters

YANG Fan1， HUANG Yong-Qing1，2， SONG Hong-Ru3
（1.Institute of Information Technology&Engineering Management，Tongling College，Tongling 244000，China；2.School of Management，Hefei University of Technology，Hefei 230009，China；3.Institute of Electric Engineering，Tongling College，Tongling 244000，China）

An improved bacterial colony chemotaxis algorithm（BCC）was proposed to optimize the parameters of PID control.When the multi-dimensional variables are optimized，the BCC algorithm is time consuming and difficult to converge.Two improved measures were put forward.The first way is to use the variable step search；the second way is to set the active area for each bacterial variable.If the new position is out of the set area，the location of the bacteria will be replaced by a fixed value or the elite value in the region.Through the PID control parameters，the simulation experiments show that the improved algorithm has a good performance in the accuracy of the parameters，the stability of the parameters and the optimization time.

PID controller；bacterial colony chemotaxis algorithm；variable step search；elite replacement

TP18

A

2015-10-20

中国博士后科学基金（2014M560508）；安徽省高等学校省级自然科学研究项目（KJ2012A269）；安徽省自然科学基金项目（1208085MG121）；教育部人文社会科学研究青年基金（11YJC630074）；铜陵学院院级科研项目（2014tlxyxs31，2015tlxy31，2015tlxy34）资助.

杨凡（1978-），女，辽宁营口人，硕士，讲师，从事进化计算研究.