黄海海战的兰彻斯特数学模型①

赵畅（吉林师范大学数学学院，吉林 长春 130103）

黄海海战的兰彻斯特数学模型①

赵畅
（吉林师范大学数学学院，吉林 长春 130103）

分析原有的兰彻斯特微分方程，根据黄海海战的相关数据资料，对此方程进行相应的修改，建立符合这场战役的兰彻斯特战斗模型.利用该模型分析战争胜负结果，找到影响战争胜负的因素，并假设适当引入现代信息化战争的科学技术，对黄海海战进行合理猜想，推测双方获胜的可能性，得出信息技术的重要性.

黄海海战；兰彻斯特微分方程；兰彻斯特战斗模型；信息化战争

0　引言

（1）黄海海战

甲午中日战争是19世纪末日本侵略中国的战争.在甲午战争中有一场著名战役叫做黄海海战，发生在在黄海北部海域，它是甲午战争中清日两军的第一次主力决战.开战之初，清军即北洋水师总兵力2126人，日军即日本联合舰队总兵力3916 人.历时5个多小时，清军死伤千余人，日军死伤600余人，此役北洋水师失利，使黄海制海权落入日本联合舰队之手，对甲午战争的后期战局具有决定性影响.

（2）兰彻斯特方程

兰彻斯特微分方程是描述交战过程中双方兵力变化关系的微分方程组.1915年，英国工程师F. W.Lancherster首次提出发表，从古代使用冷兵器进行战斗和近代运用枪炮进行战斗的不同特点出发，在一些简化假设的前提下，建立了相应的微分方程组，深刻地揭示了交战过程中双方兵力变化的数量关系.

1　兰彻斯特战斗模型建立

战争的胜负与战争双方参加战争军队的人数（兵力）成正比，而军队人数因战斗的减少和非战斗的减少，因后备军的增援而增加.

军队的战斗力是军队杀伤对方军队的能力，根据著名的兰彻斯特战斗力定律，有：战斗力=参战单位总数×单位战斗效率.

假设清军战斗减员率f只与日军的兵力n有关，则设f与n成正比.即

其中km表示日军的战斗有效率，

其中rn表示日军的进攻率，Pn表示日军每次进攻的命中率.同理，对于日军的战斗减员率g有

其中kn表示清军的战斗有效率，rm表示清军的进攻率，Pm表示清军每次进攻的命中率.

根据清日两军的减员率，可建立两军兵力变化模型：

其中：m（t），n（t）分别表示清日两军在时刻t的兵力；f（m，n），g（m，n）分别表示清日两军战斗减员率；φ（m），Ψ（n）分别表示清日两军非战斗减员率；σ（t），δ（t）分别表示清日两军在时刻t的增援率.

在分析甲午战争结局时因非战斗减员与战斗减员相比，数量很少可忽略这一项.且由于欧美列强采取默许或纵容的态度，并未对两军进行军队支持，即清日两军都没有增援，既有σ（t）=δ（t）=0.设清日两军的初始兵力分别是则建立模型.

对此微分方程组进行求解，得

由初始条件，解得

当a＞0时，存在一个时刻t1，有m（t1）=0，且n（t1）＞0.这表示清军兵力为零时，日军兵力为正值，即日军获胜.因此，

当a＞0时，日军获胜；当a=0时，两军战平；当a＜0时，清军获胜.

日军若要获胜，则需满足以下条件：

2　模型的求解与扩展

根据资料显示，可假设在黄海海战中单位时间内清军死伤1000人，日军死伤600人，有

则

可见，日军获胜的可能性很大，与历史上的实际结果相同.

当代的社会是一个信息化，科技化的社会，战斗的方式与以前有了很大的不同.假设当年清军北洋水师能够利用现在的隐藏作战技术（在隐蔽区域内活动）和雷达探测技术（准确击中目标），清日两军的其他装备依旧不变，下面根据假设对已得到的兰彻斯特战斗模型进行改进扩展.

设清军在日军看不到的某个面积为Sm的隐蔽区域内活动，日军不是向清军船只开火，而是向此隐蔽区域内开火，并且无法了解清军的死伤情况.这时，在这个有限的隐蔽区域里清军兵力越多，死伤也越多，因此清军战斗减员率不仅与日军兵力有关，而且随着清军兵力的增加而增加.有

且日军战斗的有效系数为

其中rn表示日军的进攻率，Pn表示日军每次进攻的命中率，且为日军每次进攻的有效面Sn与清军的隐蔽活动区域Sm之比.则

依旧可以忽略清军非战斗减员率φ（m），日军非战斗减员率Ψ（n），令清日两军在时刻t的增援率σ（t）=δ（t）=0.则有

解此微分方程组有

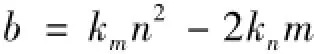
根据初始条件，解得2

同理，当b＞0时，日军获胜；当b=0时，两军战平；当b＜0时，清军获胜.

这时，清军若想获胜需满足以下条件：

即

根据英国海军年鉴的统计计算，日本舰队的火力rn相当于北洋舰队火力rm的3倍，再由假设清军利用现代信息技术，每次射击的命中率达到Pm= 1，故有

解上述不等式，有

得到清军的隐蔽活动区域Sm与日军每次射击的有效面Sn之比大于10819.654时，清军就能获胜.黄海有海域辽阔的地理条件，现代信息化的高科技可以满足这样的条件，故清军可以有以少胜多的可能性.

Lancherster Mathematical Model of Battle of Yalu River

ZHAO Chang
（College of Mathematics，Jilin Normal University，Changchun 130103，China）

Based on the analysis of the original Lancherster differential equations，according to the interrelated data of Battle of Yalu River，the equations were modified accordingly.A Lanchester combat model conforming to the battle was established.Then，the model analysis outcome of the war was used to find the influencing factors of the war outcome.The results of Yalu River Battle was conjectured reasonably according to the assumption of the appropriate introduction of science and technology of modern information war.speculated that likely to win on both sides，The importance of information technology was discussed.

Battle of Yalu River；Lanchester differential equations；Lanchester combat model；Information war

O175.1

A

1008-1402（2015）06-0819-02

2015-10-05

赵畅（1991-），女，吉林九台人，吉林师范大学数学学院在读研究生，应用数学.