基于K-均值聚类多场景时序特性分析的分布式电源多目标规划
彭春华,于 蓉,孙惠娟
(华东交通大学 电气与电子工程学院,江西 南昌 330013)
0 引言
在以大机组、大电网、高电压为主要特征的单一供电系统已不能满足对电力供应质量与安全可靠性要求日益提高的今天,分布式电源DG(Distributed Generation)以其投资小、清洁环保、供电可靠和发电方式灵活等优点日益成为人们研究的热点[1]。DG接入配电网后使得电力系统的规划和运行与过去相比有更大的不确定性,继而对配电网的有功损耗、电网运行安全性、环境与资源等产生影响。合理的安装位置和接入容量可以支撑馈线电压,改善系统电压分布,减少系统有功损耗,降低DG投资方投入[2]。因此,对一个配电系统进行规划时必须合理选择DG的安装位置和容量,其重要性可见一斑。
国内外学者对DG的规划问题已进行深入的分析与研究[3-7]。这些文献大多假设DG出力及负荷需求恒定不变,这种假设与实际情况存在差距,从而使得配网中DG位置和容量的配置方案存在不合理性。近年来也有部分文献考虑了DG出力及负荷需求在不同季节呈现出不同的时序波动性。文献[8]基于DG负荷和出力的时序特性,建立考虑环境成本的微网DG规划模型,最后采用遗传算法对规划模型进行求解。文献[9]以电能损耗和可靠性作为目标函数,在考虑DG负荷和出力时序特性的基础上,采用遗传算法对DG进行规划。但这些文献中没能考虑到DG出力往往存在很大的不确定性,在运用历史数据进行规划时,若以某个季节的单日数据值作为该季节的规划参数,忽略了DG出力值和负荷需求值在同一季节不同天中的差异,结果仍然会存在较大误差。
综上分析,为了DG选址定容规划更为准确合理,本文将通过时序特性分析考虑DG出力和负荷需求的波动性,提出采用K-均值聚类多场景概率分析法来考虑DG出力和负荷需求的不确定性,并以年寿命周期收益率和系统电压分布改善率最大化为目标构建新型的配网DG多目标规划模型,然后采用高效多目标复合微分进化算法对模型进行求解和基于最短归一化距离法实现多目标总体最优解决策,并在IEEE33节点配电系统中成功进行了DG规划应用,获得了良好的效果。
1 时序特性描述
时序特性可分为DG出力时序特性和负荷时序特性。为了更准确地进行规划,体现各种负荷模型对DG规划的影响,将负荷对象定为3类,分别为居民、工业和商业负荷。由文献[10]中的数据及图表可清楚地看出居民、工业和商业用电集中时间段有差异,且不同的负荷在不同的季节呈现出不同的规律性,因而负荷时序特性有所不同。
本文假设并网的DG为具有很强随机性、波动性和间歇性的风力发电机WG(Wind power Generation)和光伏PV(PhotoVoltaic)。风电和光伏不可能持续额定出力,而且大部分时间出力较小。采用具有典型季节性的夏季和冬季的风电和光伏在一天中的出力变化情况作为图例进行说明。由图1和图2(图中出力均为标幺值)可看出风电和光伏在不同季节的出力特性不同,且风光存在着一定的互补性。

图1 夏季风光出力对比图Fig.1 Comparison of power output between WG and PV in summer
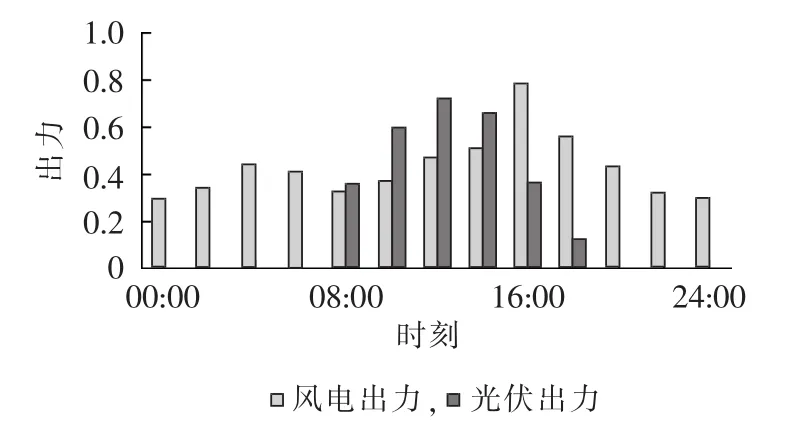
图2 冬季风光出力对比图Fig.2 Comparison of power output between WG and PV in winter
由于负荷及DG出力具有时序性,因此在进行DG规划时,考虑时序特性十分必要,否则会使规划结果产生一定的偏差,容量配置缺乏合理性,导致规划模型中反映的电网技术指标不准确,同时也会造成资源的浪费。
2 基于K-均值聚类压缩的多场景分析
多场景分析[11]是解决随机性问题的一种有效方法。多场景分析的实质就是通过将难以用数学模型表示的不确定性因素转变为较易求解的多个确定性场景问题来处理,从而避免建立十分复杂的随机性模型,降低了建模和求解的难度[12]。本文引入场景分析法来模拟随机变量在实际环境中的不确定性。从模拟随机变量不确定性的精确度考虑,场景的规模越大,得到的结果越精确,但大规模的场景增加了目标函数以及约束的计算量和计算时间。为解决不确定性模型精度与计算复杂度的矛盾,可先通过生成足够大的场景满足模拟不确定性模型的精度,再运用场景缩减法缩减至合适的场景数以满足降低计算复杂度的需求。
根据上述方法,场景模型的生成分成2个阶段[13]。本文的随机变量有光伏出力值、风电出力值、负荷需求值。第一阶段,对每个随机变量生成数量足够多的场景。首先通过对光伏出力、风电出力、负荷需求等的历史数据(如果缺乏这类历史数据,也可基于光伏、风能、负荷等对象模型,结合气象数据,利用HOMER软件产生模拟数据[14-15])进行分析统计,得到各随机变量在春夏秋冬不同季节全天各时段的典型数据,设各时段实际数据与典型数据误差ΔP服从相应的概率分布函数PDF(Probability Distribution Function),则每个场景的随机变量表达式如(1)所示。
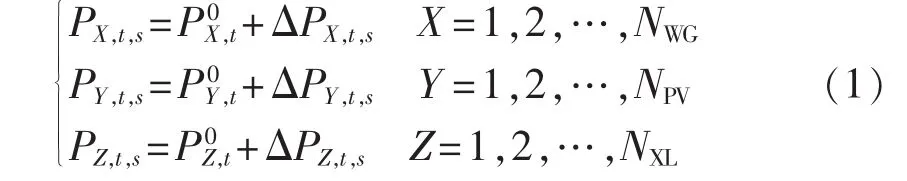
其中,s=1,2,…,Ns,Ns为场景总数;t=1,2,…,24;NWG、NPV、NXL分别为风电个数、光伏个数和系统节点数;分别为t时刻的第X个风电、第 Y个光伏的典型出力值及第Z个节点上的典型负荷需求值;PX,t,s、PY,t,s分别为场景 s 下 t时刻的第 X 个风电、第 Y 个光伏出力值;PZ,t,s为场景 s下 t时刻第 Z 个节点上的负荷需求值。
以此为依托,通过轮盘赌的方式,基于场景分析法得出不同的场景。具体的场景生成方法可参照文献[16],在此不再赘述,流程如图3所示。

图3 场景生成流程图Fig.3 Flowchart of scenario generation
PDF离散化为7个区间可如图4所示,图中横坐标表示功率误差,每个区间的宽度为功率误差的标准差σ;纵坐标为概率密度,即每个区间相对应的概率为 αb,t(b=1,2,…,7)。 图5所示的圆面积为 1,采用轮盘赌,随机生成一个0~1之间的数,选中的区间置为1(即可确定选中的概率误差),其余区间置为0,按此方法,每个场景均包含一组二进制数,由此确定风电输出、光伏输出及居民、工业、商业负荷需求的功率误差被选中的概率区间,如式(2)所示。紧接着计算每个场景的概率,并将场景概率标准化,分别如式(3)、式(4)所示。
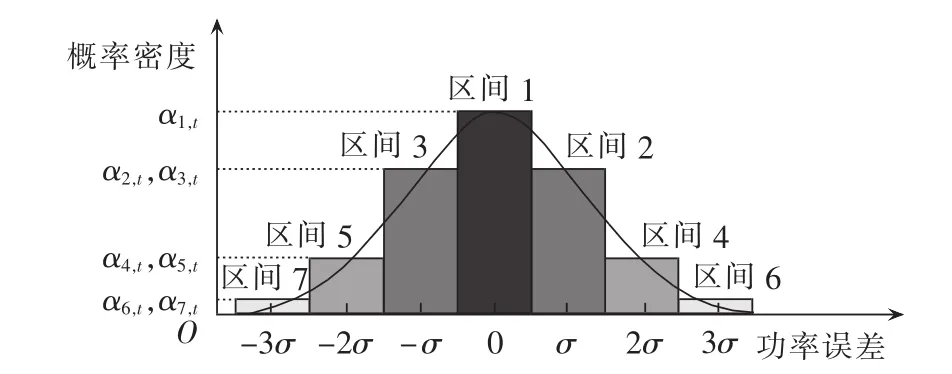
图4 功率误差的离散化概率分布函数Fig.4 Discretized PDF of power error
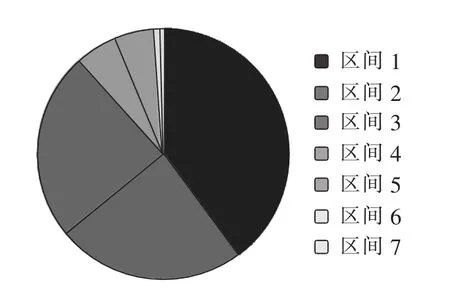
图5 功率误差区间Fig.5 Intervals of power error
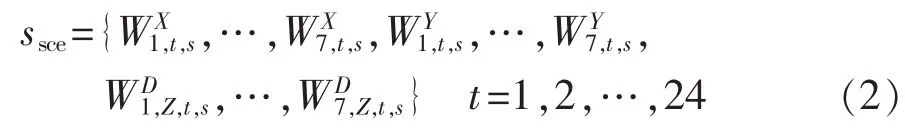

其中,ω为每一个场景 s 的可能发生概率;αx,t、αy,t、αl,Z,t分别为场景 s 下 t时刻第 x 个风电功率误差区间、第y个光伏功率误差区间、第Z个节点第l个负荷需求功率误差区间的概率。

其中,Pr为每个场景下的标准化概率。
第二阶段,对已生成的大规模场景进行缩减,得到满足计算复杂度的缩减场景。
目前常用的场景缩减方法是启发式同步回代缩减方法,其基本原则是使缩减前后场景集合之间的概率距离最小,在大规模场景下用此方法效率较低。为此本文提出采用K-均值聚类的方法对场景进行聚类,采用距离作为相似性的评价指标,将聚类后的K个质心作为保留场景,该方法简单易行,速度快,效率高,且能保证缩减后场景的多样性。
用 ξs(s=1,2,…,Ns)表示缩减前的 Ns个不同场景,对应场景标准化概率为Pr(s),假设目标场景数为Ms,场景缩减的具体步骤如下。
(1)随机选取Ms个场景作为质心,质心场景的集合为
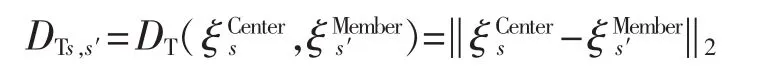
(3)根据由 DTs,s′组成的距离矩阵,将剩余场景归类到距离最近的质心。此次聚类后的聚类集合为HCluster={Ci}(i=1,2,…,Ms),其中 Ci表示同类中的场景集合。
(4)质心计算方法:假设某个聚类 Ci中有 Ls个场景,计算每个场景与其他场景的距离之和CTs=选取CTk=min(CTs)的场景ξk为新的聚类中心。按上述方法重新确定质心集合。
(5)重复步骤(2)—(4),直到质心和聚类结果不再变化,场景缩减结束。每个场景的概率值即为该类中所有场景的概率之和。
3 DG规划的数学模型
3.1 目标函数
运行经济性和电压质量是衡量配电网的两项重要指标,本文以最大化DG年寿命周期收益率和电压分布改善率作为目标函数。
3.1.1 DG年寿命周期收益率
综合考虑了年均全寿命周期收益现值与年均全寿命周期成本现值。年寿命周期收益率在数值上等于DG投入运行后全寿命周期内获得的年均收入现值与年均投资费用现值之比。简化的年寿命周期成本包括DG初期投资、年运行维护费用、年直接停电损失费用、年购电成本;年寿命周期收益包括DG上网卖电年收入、年电价补贴收入和用户年售电收入[17]。

其中,Bp为年寿命周期收益;Cp为年寿命周期成本。
a.年寿命周期成本:
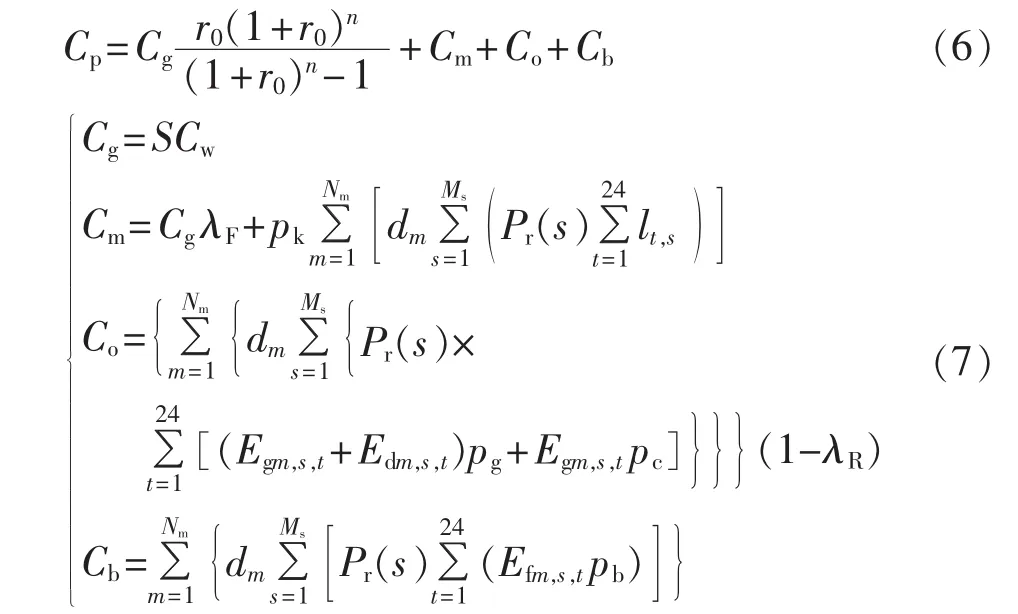
其中,Cg为DG的初期投资费用;r0为折现率;n为经济使用年限;Cm为DG年运行费用;Co为年直接停电损失费用;Cb为年购电成本;S为DG的装机容量;Cw为单位装机容量成本;λF为DG运行维护率;pk为平均售电价格;Nm为季节数,取4;dm为第m个季节的相应天数;Pr(s)为场景 s的概率;lt,s为加入 DG 后配电网在场景 s 下 t时刻的网损;Egm,s,t和 Edm,s,t分别为并网DG在第m个季节场景s下t时刻的上网电量和自发自用电量;Efm,s,t为在第 m个季节场景s下t时刻(配电网提供电源)的用电量;pg为政府补贴电价;pc为当地燃煤机组标杆上网电价;pb为第三方投资者的购电电价;λR为供电可靠率。
b.年寿命周期收益:
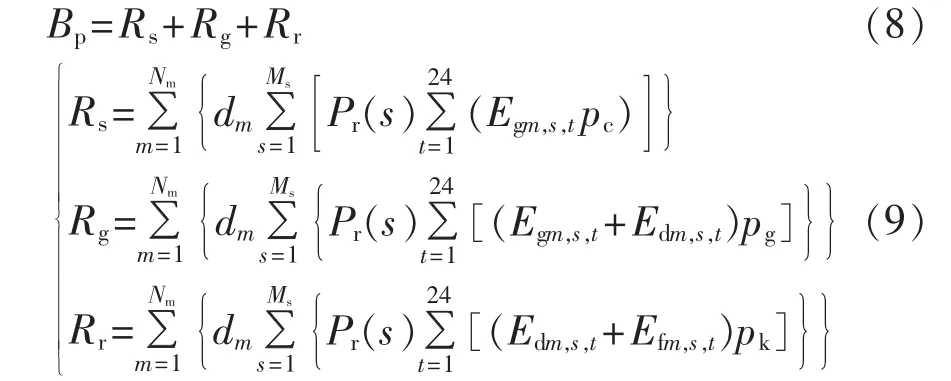
其中,Rs为DG年上网卖电量收入;Rg为年电价补贴收入;Rr为用户年售电收入。
3.1.2 电压分布改善率
系统接入DG后,由于馈线上的传输功率减小以及DG输出有功和无功的支持,各负荷节点处的电压被抬高,部分线路电流减小,使得系统的电压分布得到改善[18]。DG在配网中合理接入位置及容量配置将使得系统电压分布的改善作用大幅增加。定义电压分布改善率指标为:

其中,UPw为含DG时系统年电压指标;UPwo为不含DG时系统年电压指标。
加入多场景的电压指标计算公式如下:
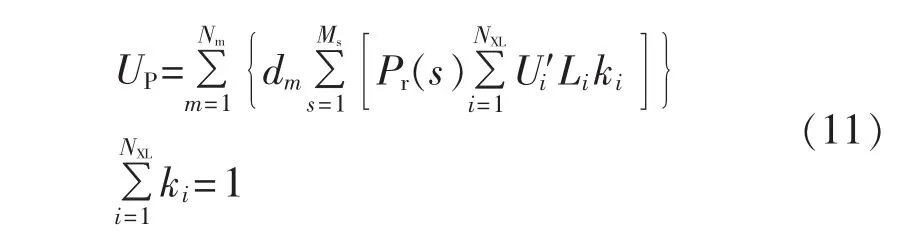
其中,NXL为系统节点数;U′i为节点i的电压幅值,但只包括电压不越限时的情况,通常使用的电压范围是 0.95 ~1.05p.u.[18];Li为节点 i的负荷值;ki为节点i负荷的权重因子,该值将系统中各节点负荷重要程度量化,以体现系统中的负荷重要程度的不同。
3.2 约束条件
(1)节点潮流方程约束:

其中,Ui和 Uj分别为节点 i、j电压;PGi和 QGi分别为节点i处电源的有功和无功出力;PLi和QLi分别为节点i处的有功和无功负荷;Gij和Bij为系统导纳;δij为节点电压相角差。
(2)节点电压约束:

其中,Ui为节点i的电压;Uimax和Uimin分别为节点i的最大允许电压和最小允许电压。
(3)导线电流约束:

其中,Ii为第i条支路的电流;Iimax为第i条支路的最大允许电流。
(4)单个节点接入DG容量限制:

其中,PDG为每个节点接入DG的有功功率;PDGmax为每个节点允许接入DG最大有功功率。
(5)DG容量选择约束:
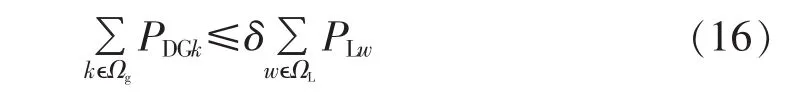
其中,δ为DG的容量渗透率;PDGk为第k个DG的出力;PLw为节点w的负荷;Ωg为DG接入的节点集;ΩL为配电网负荷节点集。若容量渗透率极限过高,将可能引发电压调节和继电保护的很多问题[19],因此应该将DG的渗透率限定在一个较为合理的范围内。
4 基于复合微分进化算法的多目标规划
4.1 多目标复合微分进化算法
对于一些复杂的优化问题,目标函数不连续、不可微,还可能存在大量的局部极值点,传统经典算法要找出全局最优点非常困难[20],而复合微分进化CDE(Compound Differential Evolution)算法在全局优化方面有明显优势。CDE算法主要通过个体排序、种群分割、按不同的变异策略进化及种群重组这几个步骤来兼顾收敛速度和个体多样性[20]。CDE算法在继承微分进化DE(Differential Evolution)算法易于使用、鲁棒性强和全局搜索能力好等优点的同时,又能有效地解决DE存在的种群进化过程中收敛速度和个体多样性之间存在的矛盾。
在CDE算法的基础上,引入Pareto非劣等级和拥挤距离排序等操作,提出了非劣排序复合微分进化NSCDE(Non-dominated Sorting Compound Differential Evolution)算法,该算法将Pareto非劣排序操作与CDE算法有机融合,并对个体间的拥挤距离计算进行改进以克服搜索不均的问题。该算法使解具有多样性,计算速度快,且不容易早熟,在多个测试问题上表现出的搜索性能优于其他多目标算法。
4.2 多目标总体最优解决策
通过多目标优化算法可求得一系列Pareto最优解,实际应用时通常还须从中决策出最终实施方案。为此本文提出基于最短归一化距离的多目标总体最优解决策方法。针对本文研究的多目标规划问题,可首先根据最终得到的Pareto最优前沿确定出在满足所有约束条件下年寿命周期收益率JBC和电压分布改善率JUP的上下限,然后构造如式(17)所示的模糊隶属度函数[22]对各非劣解对应JBC和JUP两目标的满意度 hBC和hUP在[0,1]区间内进行量化评估(当为0或1时分别代表对某个目标函数值完全不满意或完全满意)。

这样可将各非劣解映射到一个归一化的多目标满意度空间中,该空间各坐标轴范围均为[0,1];在此空间中可定出一个假想的使所有目标都达到最优的虚拟理想解B,它的位置坐标为(1,1);然后分别计算出各非劣解映射在多目标满意度空间中的位置与B之间的距离,并进行相互比较;其中与B距离最短的非劣解最接近理想解,其总体满意度最高,因此可将其确定为总体最优解,便可从Pareto最优解集中自动决策出一个最佳方案以供实施。基于最短归一化距离的总体最优解决策方法的示意图如图6所示。
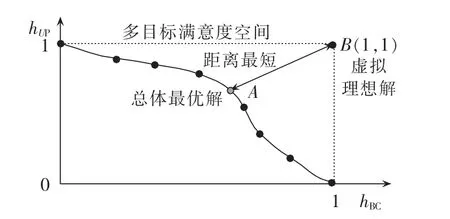
图6 总体最优解决策方法示意图Fig.6 Schematic diagram of decision-making for overall optimal solution
综合上述过程,本文采用的基于NSCDE算法的多目标DG规划流程如图7所示,图中niter、nitermax分别表示当前迭代次数和最大迭代次数。
5 算例研究
5.1 参数设置说明
本文按照上述模型和算法,对典型IEEE 33节点系统进行DG位置和容量的规划。根据该地区的负荷特点,对各节点的负荷类型进行如下假设:节点2—10为商业负荷,节点11—25为居民负荷,节点26—33为工业负荷。根据实地考察,风电的待选安装节点为 5、9、15、16、17、21、25、28、31、33,光伏的待选安装节点为 3、6、10、17、18、22、23、28、29、31。本算例中的配电系统结构及线路参数来自文献[23],如图8所示。
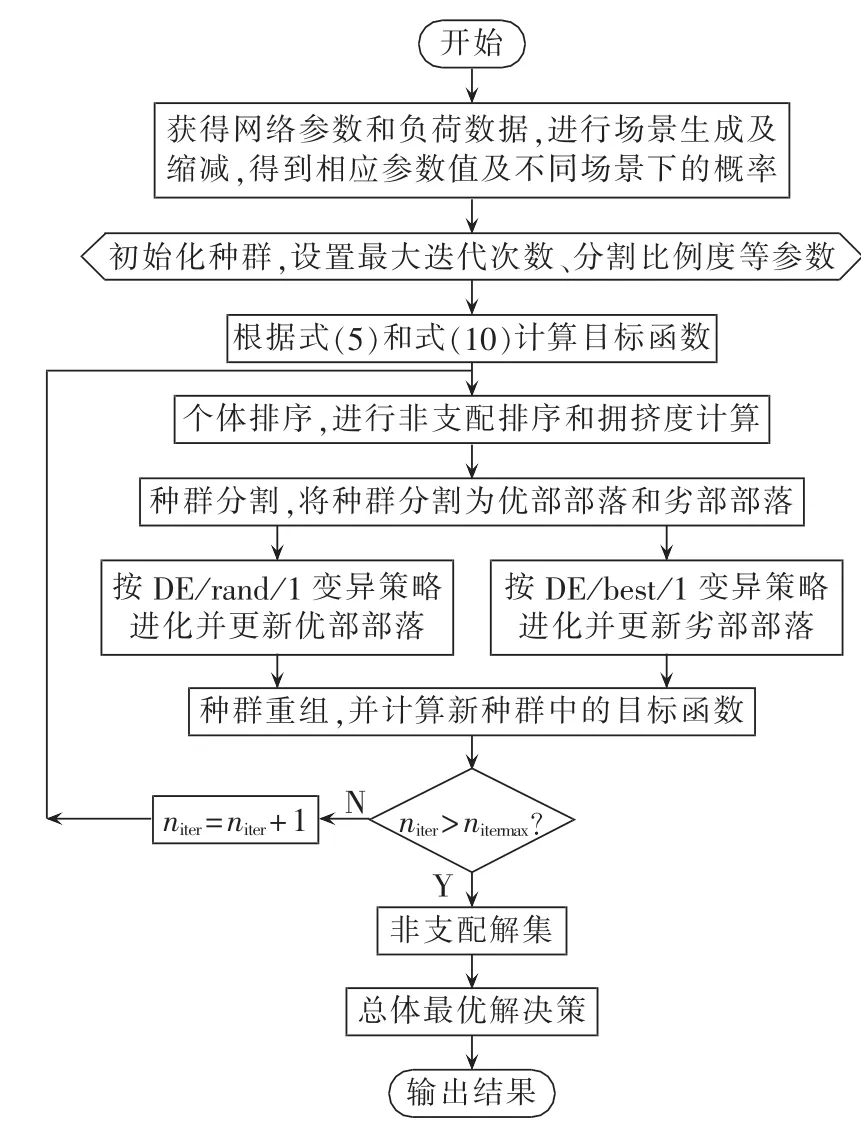
图7 基于NSCDE算法的DG规划流程图Fig.7 Flowchart of DG planning based on NSCDE algorithm
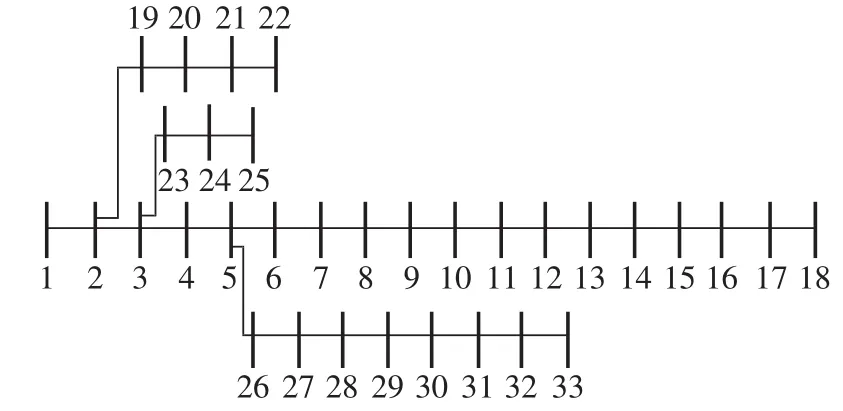
图8 IEEE 33节点配电系统图Fig.8 IEEE 33-bus distribution system
假设在4个节点安装风电和光伏,风电投资成本为1.3×104元/kW,光伏投资成本为4.55×104元/kW,设备寿命周期为25 a,折现率为8%,光伏上网电价为0.95元/(kW·h),风电上网电价为0.61元 /(kW·h),政府补贴为 0.25 元 /(kW·h),DG 运行维护率是0.03,平均售电价格为 0.65元/(kW·h),DG在电网中的最大渗透率不得超过全网负荷的30%。本算例中风电出力、光伏出力以及各类负荷需求在春夏秋冬四季的日典型数据来自文献[8-9],采用本文方法随机生成500个场景,再通过K-均值聚类方法缩减成10个场景并分别得到各场景的概率。以春季的风电出力为例,其生成的10个场景的概率如表1所示。本算例中NSCDE算法选取交叉概率为0.6,变异尺度因子为0.3,种群分割比为1∶1。
5.2 结果分析
为验证K-均值聚类方法对场景缩减的有效性,将生成的500个场景通过K-均值聚类方法缩减为40个场景,并以春季时风电在05:00、10:00、15:00、20:00这4个时刻的出力为代表,刻画出力分布图,如图9所示(图中出力为标幺值)。由图可知,通过场景生成,并经由K-均值聚类法缩减后,这4个时刻的功率分布基本服从以各自时刻出力值为均值的正态分布,数据能够较好地保持场景的多样性。
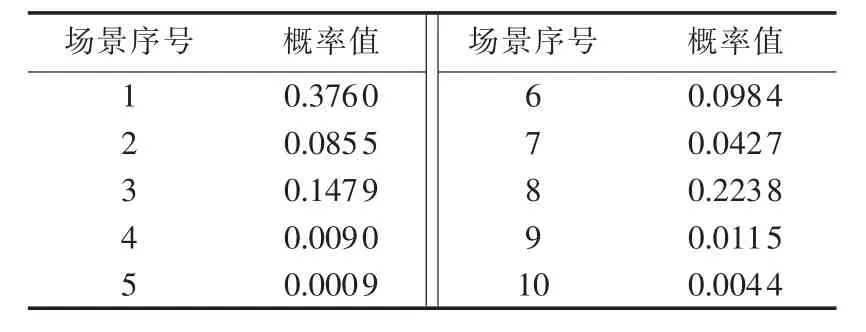
表1 春季风电出力场景概率表Table 1 Probability of WG output scenarios in spring

图9 4个时刻风电出力分布图Fig.9 WG output distribution for four moments
为说明随机场景生成的有效性,以春季光伏出力为例,所生成的10个场景出力曲线与历史典型出力曲线对比关系见图10(图中出力为标幺值)。可见所生成的不同场景具有较好的代表性,能够较全面地反映光伏出力在一定区间范围内的随机特性。限于篇幅,其他典型场景与生成场景的曲线对比不再列出。

图10 春季光伏出力场景图Fig.10 Scenarios of PV output in spring
在加入时序特性的基础上,考虑多场景和不含多场景2种模式,程序运行1000代,得到的Pareto前沿见图11。由图可看出,是否考虑多场景,Pareto前沿存在明显差异,对DG规划有较大的影响。在进行多场景分析后,由于充分考虑了DG出力及负荷需求的不确定性影响,使得在同样的DG年寿命周期收益率情况下,系统电压分布改善率得到一定提高。这是由于考虑了不确定性影响,增大了风光出力之间的互补概率及DG发电与负荷需求之间的匹配概率,这进一步说明了考虑多场景分析的重要性。
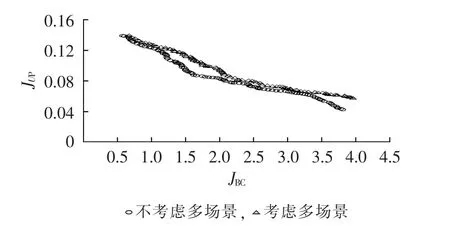
图11 2种模式下的Pareto前沿Fig.11 Pareto frontier for two modes
表2列出了考虑多场景时序特性模式下的部分Pareto最优解,其中方案3为采用基于最短归一化距离法得出的Pareto最优解。
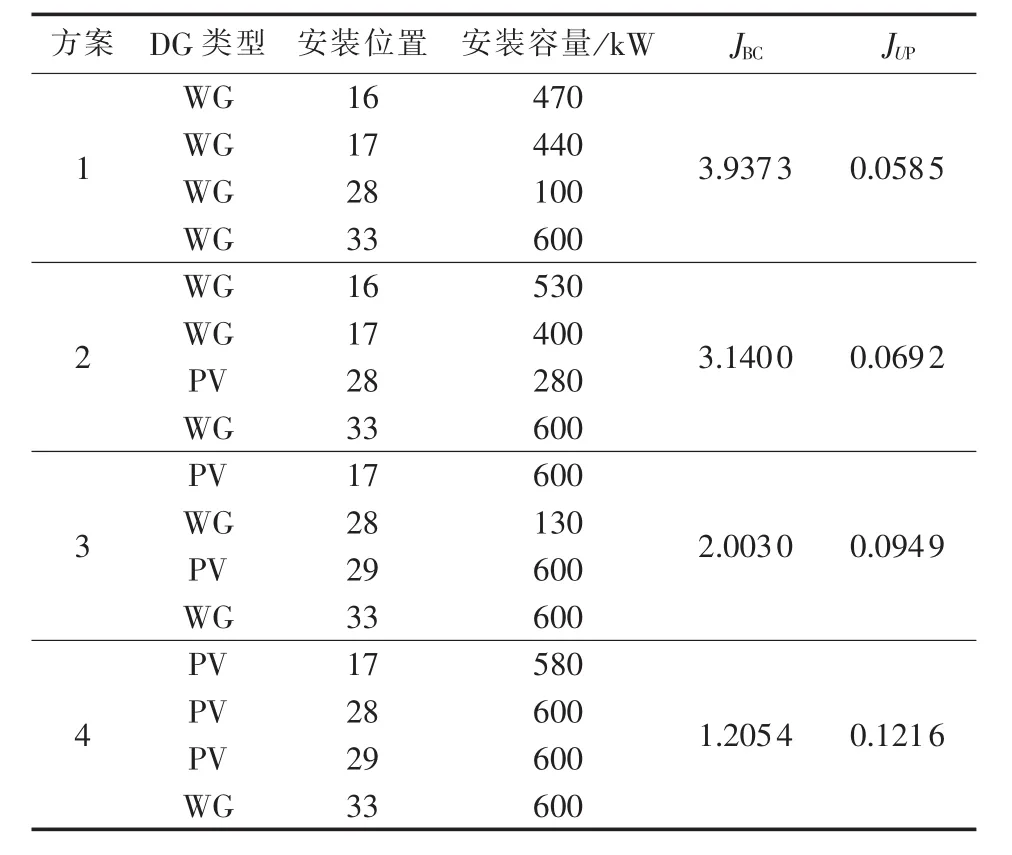
表2 不同方案下的结果比较Table 2 Comparison of results among different schemes
随着风电和光伏的配比及容量和位置的变化,DG年寿命周期收益率JBC和电压分布改善率JUP发生改变,年寿命周期收益越大,年寿命周期成本越小,即JBC越大,取值越优;JUP为加入DG后电压分布改善率指标,其值越大越优。由于JBC与JUP存在一定的矛盾性,同时使得这2个目标函数达到最优的可能性很小。因此在实际的DG规划中,决策者可根据自己的偏好并结合实际情况进行有效合理的选取。从表2中可明显看出,随着风力发电机数量的增加,即光伏发电机数量的减少,JBC值不断增加,这主要是由于风力发电机目前的造价较低,而光伏发电机的造价较高,多安装风力发电机能降低投资商的投资成本,提高收益;而随着风力发电机数量的减少,即光伏发电机数量的增加,JUP值不断增加,这主要是由于风光互补后,出力时序曲线与负荷时序曲线达到较好的匹配效果,更有利于改善系统的电压分布。
因此,若在资金较为充裕的情况下,可以以提高电压分布改善率为主,适当地增加光伏发电机的安装数量,以改善系统的电压分布;若在资金有限的情况下,可以以提高年寿命周期收益率为主,适当地增加风力发电机的安装数量,以降低年寿命周期成本,提高年寿命周期收益。若规划者没有特别的偏好,可根据基于最短归一化距离法进行多目标总体最优解决策。
表3为时序和多场景均不考虑、仅考虑时序不考虑多场景以及时序和多场景均考虑3种模式下所得到的多目标DG规划总体最优解。第一种模式下不考虑出力时序波动特性,将风电和光伏的出力简化为恒定输出,这无疑是不切合实际的,此时2类DG在JUP上体现不出区别,导致投资成本较低的风力发电机成为最优选择,尽管得到的方案具有较大的收益率JBC,但缺乏合理性。在考虑时序特性的基础上,是否加入场景分析法,对于规划结果也有较大影响。加入场景分析法,考虑了在时序基础上的不确定性,能更好地反映出实际。从表3中可看出,采用本文所提出的多场景时序特性分析方法,所得到的总体最优解在JBC和JUP两方面均有改善。
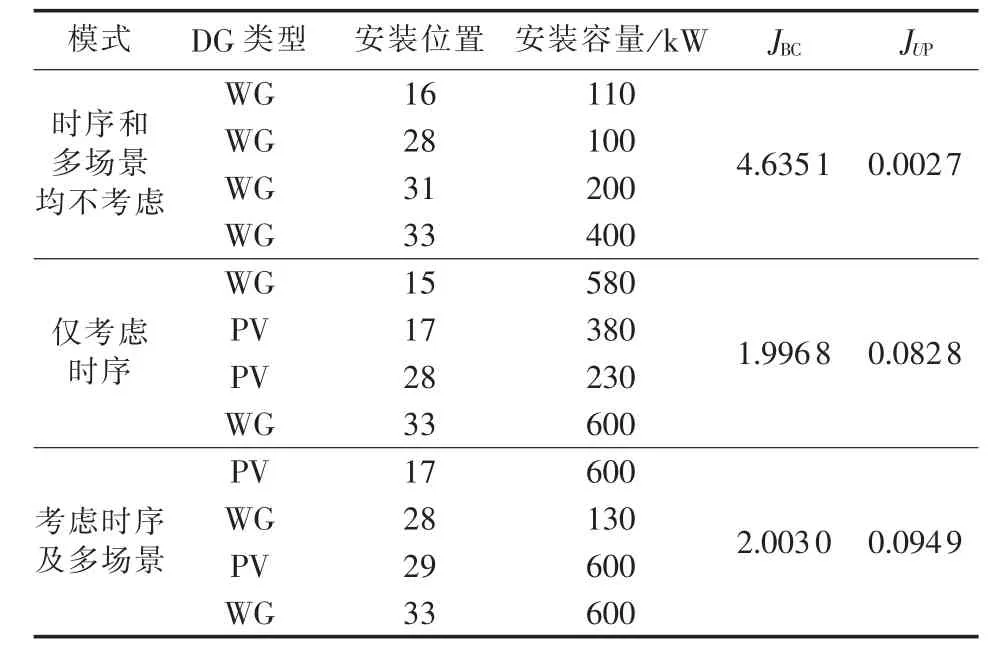
表3 各模式下的规划结果Table 3 Planning results of different modes
6 结论
本文在考虑负荷和出力的时序特性的基础上,加入K-均值聚类多场景分析法,以年寿命周期收益率和电压分布改善率作为目标函数,采用多目标CDE算法求解该规划问题。主要结论如下。
首先,加入多场景时序特性十分必要,这样能更真实地反映实际情况。时序特性能体现光伏和风力发电各自随自然条件的变化规律及负荷需求的变化趋势,而多场景则在其基础上考虑了同一季节每日间的不确定差异性,从而达到更为准确的规划效果。
其次,采用多目标算法能够对不同的目标函数进行协调,避免函数之间的冲突。根据实际情况,决策者能够有方向性地进行有效合理的规划。
本文的研究可为配网DG规划中建模、优化控制及优化算法的发展提供新思想,为今后DG的规划提供一定的理论依据。

