基于热力耦合有限元模型的弹带挤进过程及内弹道过程的仿真研究
丁传俊,张相炎(南京理工大学机械工程学院,江苏南京210094)
基于热力耦合有限元模型的弹带挤进过程及内弹道过程的仿真研究
丁传俊,张相炎
(南京理工大学机械工程学院,江苏南京210094)
为了更好地揭示弹带和身管的相互作用过程,建立了弹炮热力耦合有限元分析(FEA)模型,采用Fortran子程序结合显式有限元方法对挤进过程以及随后内弹道过程进行了数值模拟。计算结果和实验数据对比验证了热力耦合模型的准确性。仿真结果表明:采用经典内弹道模型时,次要功系数随时间变化并存在极值;在挤进过程中,弹带表层受热软化对内弹道过程有显著影响;对于药筒定装式炮弹,计及拔弹力可以提高挤进过程及随后内弹道过程的计算精度。
兵器科学与技术;弹带挤进;热力耦合;拔弹力;有限元方法
0 引言
自动炮发射过程中,弹带挤进过程对随后的内弹道及外弹道过程有着非常重要的影响。火药点火后,弹丸首先要克服拔弹力才能启动。由于存在定位间隙,弹带一般先要经过一段空行程才开始和坡膛、膛线相接触,进而嵌入膛线直到完成整个内弹道过程[1]。
由于内弹道挤进过程时间极其短暂,加上难以观察和测量,在实物实验方面除了采用静压法和截短炮管的方法,鲜见其他研究手段分析这一过程。在数值仿真方面,多位研究人员分别进行了细致并富有成效的研究。文献[2]专门研究了挤进时期的内弹道,其认为内弹道计算过程中的次要功系数不应该是定值,挤进完成后的内弹道压力应该高于30MPa.文献[3]基于弹带材料损伤模型的研究,分别分析了两种不同坡膛结构对弹带挤进过程的影响,为火炮坡膛的设计提供了有益参考。文献[4]研究了铜/钢接触摩擦系数与温度之间的关系,认为在高速重载情况下,铜/钢接触摩擦系数会随着温度变化而变化。文献[5]基于ABAQUS有限元软件建立了枪弹挤进过程的有限元模型,通过应用动态显式算法和网格自适应技术研究了挤进后弹丸的变形和残余应力,为仿真建模提供了思路。文献[6]通过金相显微镜和扫描电镜研究了回收砂弹的弹带表层微观组织,认为弹带表层经历了高温并存在热软化现象,且摩擦产生的热软化膜抑制了塑性变形向内层延伸。文献[7]通过设定不同的摩擦系数,研究了弹丸卡膛过程中弹带摩擦力对卡膛过程的影响。文献[8]分析了定装式炮弹内弹道起始压力,认为药筒定装式炮弹的拔弹力不可忽略,启动压力应该是拔弹力和挤进阻力的叠加,在内弹道研究中应当设定启动压力为50 MPa.文献[9]研制了一种弹带挤进实验装置,为研究弹带准静态挤进过程提供了实验参考。
在以上研究中,多数学者采用弹底加载实测内膛压力曲线的方法,采用这种方法相当于计及了两次次要功,其弹丸出膛参数的准确程度不高。而且,根据回收的砂弹和铜/钢干摩擦实验结果来看,弹带表层材料的受热软化(甚至融化)直接影响着弹丸的运动特性,所以不能不计及热因素的影响。因此,根据以上研究成果,本文基于ABAQUS有限元软件建立了考虑材料热软化特性和拔弹过程的弹带挤进热力耦合有限元分析(FEA)模型;通过编写弹丸弹底推力子程序(VUAMP),实现了内弹道方程组耦合弹带挤进过程的双向求解;通过编写材料摩擦力子程序(VFRICATION),研究了弹带表层温度升高对材料特性和接触界面摩擦系数的影响。数值结果表明,采用热力耦合模型和子程序式的加载方式能够准确地求出弹带挤进过程参数和内弹道参数;热力模型能从一定程度上印证文献[6]的研究成果;拔弹力对药筒定装式炮弹的内弹道计算过程的影响不可忽略。
1 挤进过程FEA模型的建立
1.1基本假设
1)弹带材料为各向同性材料,且热物理性能参数(比热容、热导率、弹性模量)随温度变化而变化;
2)弹体为弹性体,身管设定为刚体。弹带为弹塑性体,其屈服强度服从Mises屈服准则;
3)弹丸、弹带和身管初始温度恒定(25℃),同时由于内弹道时间很短,不考虑弹带的自由对流换热和辐射放热。
1.2有限元模型
根据23-2型航空自动炮内膛和弹丸的实际尺寸,本文对其进行了必要的简化后建立了有限元模型。内膛部分由坡膛、膛线构成,弹丸部分由弹体和弹带构成,其中弹带和坡膛之间有一定的定位间隙。图1为装配后的有限元模型。

图1 挤进过程的FEA模型Fig.1 FEA model of bearing band engraving process
身管部分采用C3D8RT热力耦合单元,为了节约计算成本将身管设定为刚体,并固定在空间一定位置处。弹丸和弹带部分采用C3D8RT单元,同时对弹带部分细化网格,多次计算结果表明弹带单元尺寸为0.2 mm时,可以保证计算精度且计算时间较少。在挤进过程中,对弹带网格集合采用网格自适应技术,这样可以防止弹带材料的剧烈变形而导致计算的终止。弹体和弹带之间设定TIE约束,以保证弹带和弹体之间不会发生相对运动。弹丸底部加载压力载荷 pD,载荷的幅值来自推力子程序(VUAMP)。铜/钢之间的法向接触设定为通用接触(罚方法),摩擦力由摩擦力子程序(VFRICATION)确定。
对弹带材料采用能够描述材料的热黏性行为的Johnson-Cook本构模型[10-11]:

采用包含内聚力失稳断裂的损伤本构模型来描述弹带材料的断裂失效。当材料出现损伤时,用等效塑性临界应变εd作为损伤的激活判据,εd与材料应力三轴度η、应变率、温度有关,其公式如下:

式中:d1~d5为材料参数[12]。用损伤演化过程描述材料刚度下降:

2 挤进过程的热力耦合方程
由于内弹道时间非常短暂,在弹带挤进过程及其随后内膛运动过程中,由热辐射和热对流造成的热损失可以忽略不计。热生成可以认为来自于两部分:1)材料的塑性变形热Tp,设定塑性热转化系数为0.9;2)接触界面的摩擦热Tf.因此总的热生成量可以由(4)式表示:

式中:ρ和c分别为密度和比热容;σ和ε分别为应力和应变;β为塑性热转化系数;T0为初始温度。
2.1传热模型
三维非稳态、变物性的热传导微分方程为

式中:ρ和c(T)分别为弹带材料的密度和比热容;T为弹带材料温度;kx、ky、kz分别为3个方向的热传导系数;Q为内热源,一般指塑性热。
2.2定解条件
热传导问题必须具备的单值性条件有时间条件、几何条件、热物性条件以及边界条件。
1)时间条件,是指起始时刻身管、弹带和弹丸的初始温度分布T0(x,y,z),在本文中设定为25℃;
2)几何条件,是指弹带起始时刻的形状和尺寸;
3)热物性条件,是指弹带材料物理特性随温度变化而变化的特性,其中热传导系数k、比热容c和弹性模量E均随温度变化而变化,如图2所示。

图2 弹带材料的热物理参数Fig.2 Thermal properties of bearing band
4)边界条件,根据弹带和内膛的接触条件可知,若物体边界上的热流密度为已知,则其第2类边界条件可以表示为

式中:q(x,y,z,t)为摩擦接触界面的热流密度。铜/钢接触界面接触热导设定为10 000W/(m2·K),接触界面摩擦热分配系数由(7)式决定[13]:

式中:q1、q2分别为钢界面和铜界面热流分配系数;ρ1、ρ2分别为两种材料的密度;c1、c2分别为两种材料的比热。
3 摩擦力子程序和推力子程序的实现
关于经典内弹道方程中的次要功系数φ(t),文献[2]认为该系数不应当是常数,在最初阶段φ(t)的值应该为1.其原因是内弹道的最初阶段弹丸的动能较小,而塑性功和摩擦功相对较大;而在内弹道末期,弹丸的动能很大,塑性功和摩擦功相对很小。本文采用实时求解φ(t)表达式的方法,在内弹道时期的每一时刻实时输出φ(t)值并用于内弹道计算。φ (t)所需参数的传递和计算分别通过摩擦子程序和推力子程序完成,二者均用Fortran语言编写。
3.1摩擦力子程序(VFRICTION)的实现
文献[4,6]认为,在膛内摩擦运动过程中,铜质弹带表层温度迅速升高并形成软化了的薄膜。由于这层薄膜的存在,弹带和内膛表面的摩擦将有所缓解。而当弹带材料受热软化时,其强度下降,弹带更容易发生变形和损伤,因此摩擦系数主要与相对运动速度、接触压力以及界面温度有关。挤进过程中弹带的接触压力和运动速度都很高,通过拟合高速、重载条件下铜/钢摩擦热的试验数据,本文得到摩擦系数关于温度的表达式:


式中:τf为摩擦剪应力;μ(T)为摩擦系数;p为接触压应力;σy为材料的屈服应力。
在摩擦力(VFRICATION)子程序中,将(8)式和(9)式改写,同时定义塑性功和摩擦功的公共块以方便和推力子程序通信。子程序历遍弹带的每一个接触单元,计算此时的摩擦系数μ(T)、摩擦应力τf、塑性功Wp和摩擦功Wf,并将塑性功和摩擦功传递到推力子程序中用于计算次要功系数φ(t).
3.2推力子程序(VUAMP)的实现
本文没有采用弹底加载内膛压力的加载方式,而采用子程序式的加载方式,其实现过程如下:t0时,在VUAMP子程序中设定药室内火药已然量Z0,并计算相应的内膛压力p0、弹底压力pD;压力pD传递到ABAQUS有限元软件中,当压力达到一定值后,弹丸克服拔弹力而启动;经过Δt时间间隔之后,弹丸获得平动速度v、旋转角速度Ω、位移U、塑性功Wp和摩擦功Wf;将v、Ω、U、Wp、Wf传回到VUAMP子程序中计算Δt时间间隔后的次要功系数φ(t)、火药燃烧量Z、内膛平均压力p、弹底压力pD并再传递到ABAQUS软件中去;由此循环一直到弹丸出膛、内弹道过程结束。
为了方便使用Fortran语言编程,对经典内弹道方程组进行改写,改写后的内弹道方程组分为一个主要方程和3个辅助方程。对主要方程采用4阶龙格-库塔法求解,其式如下:

3个辅助方程为

综上所述,总体计算流程设计如图3所示。

图3 仿真流程示意图Fig.3 The flowchart of simulation
4 有限元模型验证及结果分析
4.1有限元模型的验证
为了验证所构建模型的准确性,本文首先使用参考文献[2]的方法进行了计算,计算参数和计算结果如表1所示,全行程上的弹带嵌入阻力最大值为38 841.9 N,和挤压试验相差-9.2%.使用本文所建立的热力耦合模型求得沿身管轴向最大挤进阻力为40 221.4 N,和挤压试验相差-4.5%;使用热力耦合模型求出的出膛速度为710m/s,最大平均膛压pmax为344.5MPa,分别较实弹射击高出0.7%和 4.5%,弹带嵌入膛线后,内膛平均压力为131MPa.应当指明,若采用文献[2]中所述方法,首先要求出弹带换算宽度(14.9mm)以及3个接触阶段的接触面积,再求出3个阶段的接触应力和接触阻力,由于这种方法本质上是二维平面应力方法的近似,因此准确度不高。同时表中也列出了23mm截短身管在18℃时,采用静态挤压实弹的方法获得最大阻力为42 140N.

表1 研究方法以及结果Tab.1 Research methods and results
4.2热力耦合模型与弹底加载内膛压力模型的对比
计算完成后对结果进行分析,图4为挤进完成后弹带的变形图,和回收的实弹相比弹带变形一致。图5为热力耦合模型子程序输出的内弹道压力和弹丸速度。通过和实测结果比较发现,压力最大值误差4.5%、速度最大值误差0.7%,说明了本文仿真模型的有效性和准确性。弹底加载内膛压力模型(文献[5])和实测结果相差较大,弹丸线速度为684.7m/s,这是因为采用直接加载内膛压力曲线的方法,本质是计及了两次次要功,所以弹丸动能相对减少。图6为子程序输出的内弹道次要功系数随时间变化图,从中可以看出在起始时刻次要功系数较低(1.075),这是因为在弹丸在启动后弹带和坡膛相接触,此时弹带处于弹性变形阶段,因此不存在塑性变形功和摩擦功;在挤进膛线过程中,次要功系数达到了最大值1.384,而此时弹丸速度较低,说明此时的塑性功和摩擦功占据主要地位;当挤进完成后,弹带塑性变形量减小,而随后摩擦功逐渐增大,但总体来说次要功系数稳定在1.175左右。这一结论证明了文献[2]的观点,其认为起始时刻次要功系数应该为1,挤进末期该值应当下降到稳定值(1.158).文献[1]给出值1.25,但该值不能反映出挤进过程中能量的分配比例。

图4 挤进后的弹带变形图Fig.4 Deformation of bearing band after engraving
4.3热力耦合模型与不计及热因素模型的对比
从表1可以看出,若不计及挤进过程中弹带的热因素,弹带在挤进完成时的最大阻力比静态挤压情况下的最大阻力增大了19.5%,弹丸速度较实测速度增大2.6%.图7是二者速度和内弹道压力对比,当不计及热因素、次要功系数为定值、摩擦系数不变时,弹丸出膛参数、内弹道参数和实测数据相差比较大。原因在于当不计及热因素时,弹带材料相对较“硬”而难以变形,导致接触阻力和摩擦力增大。当弹带表面材料温度升高到一定温度时,弹带和内膛表面接触处会形成一层接触薄膜,此时的摩擦系数会降到稳定状态(0.1左右),而使用定值的摩擦系数无法反应这一过程。图8和图9分别为热力耦合模型在弹带挤进初期和弹带挤进完成时的温度分布图,从图中可以看出,弹带沟槽内的温度比弹带其他部位温度要高,在嵌入初期,刻槽表面的最大温度上升到134.7℃;当挤进完成后,刻槽表面后半段最高温度394℃,这一结论证明了文献[6]的结论,其认为在挤进结束后弹带摩擦表面温度应该超过材料的再结晶温度(约280℃).但是由于挤进时间较短,热量并没有向弹带内部过多的传导,弹带内部部分区域的温度依然为起始时刻的温度。

图5 速度和压力对比Fig.4 Velocity vs.chamber pressure

图6 次要功系数变化图Fig.6 Coefficient of secondary work

图7 速度和压力对比Fig.7 Velocity vs.chamber pressure

图8 挤进初期温度分布图Fig.8 Temperature field of band at the beginning of engraving

图9 挤进完成后温度分布图Fig.9 Temperature field of band after engraving
4.4计及拔弹力模型与不计及拔弹力模型的对比
由于拔弹力只影响很短的一段行程(约3mm),根据文献[8]和拔弹力试验结果发现,当弹丸受到的推力大于拔弹力而使弹丸启动后,拔弹力将迅速下降。在计及拔弹力的VUAMP子程序中,通过添加与弹丸运动方向相反的拔弹阻力13 760 N(拔弹力测试方法见文献[8]),本文实现了计及拔弹力的仿真。由于拔弹力和挤进阻力的作用时期并不完全重叠,当拔弹完成以后,由弹底压力换算而来的推力已经达到79 150 N.图10和图11分别是考虑拔弹力和不考虑拔弹力的内膛压力、速度和次要功系数的对比图。从图中可以看出,当不计及拔弹力时弹丸提前启动,并以一定速度和内膛表面相接触,次要功系数最值高达1.616,这说明塑性作功和摩擦作功之和超过正常范围;由于弹丸提前启动和弹后空间迅速扩大,在不考虑拔弹力的仿真中,内弹道峰值压力(243.6MPa)和弹丸最大线速度(602.9m/s)均低于正常值,分别为正常值的74.3%、85.4%,且弹丸未出膛(0.734m).
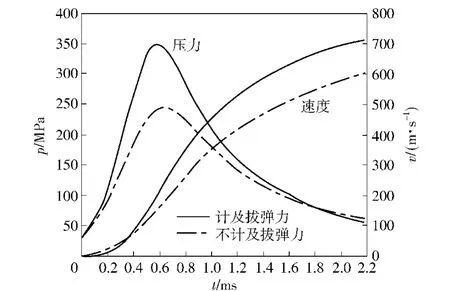
图10 速度和压力对比Fig.10 Velocity vs.chamber pressure
5 结论
本文建立了弹带挤进热力耦合有限元模型,通过数值计算与静态挤压试验及实弹射击数据相比,验证了本模型的准确性。通过分析3种影响弹带挤进以及随后内弹道过程的因素,本文得出如下结论:
1)弹带挤进计算过程中,若直接在弹底加载内膛压力,弹丸出膛速度将会偏低,原因是这种加载方式计及了两次次要功。采用有限元软件结合Fortran子程序的方法,不仅可以计算出准确的内膛压力,而且可以获得相应的出膛速度。同时结果显示,经典内弹道方程中的次要功系数不为常数且在挤进完成后出现最大值。

图11 次要功系数变化图Fig.11 Coefficient of secondary work
2)铜质弹带在挤进过程中塑性功和摩擦功将转化为热,从而使弹带材料力学特性发生改变。如果不计及弹带的温升,弹带材料相对较“硬”而难以变形,这将导致计算出的内膛压力异常、弹丸出膛速度过大;同时使用热力耦合模型计算发现,挤进完成后弹带刻槽外表面的温度已经超过材料的再结晶温度,因此热生成对材料的影响不能忽略。
3)对于小口径定装式炮弹来说,由于拔弹力相当于静态挤进阻力的1/3,在挤进过程中如果忽略拔弹力将导致内膛压力和弹丸速度偏低。
(References)
[1]何志强,黄守仁,李载弘.航空自动武器设计手册[M].北京:国防工业出版社,1991:190-216. HE Zhi-qiang,HUANGShou-ren,LIZai-hong.Handbook for airborne automatic weapon design[M].Beijing:National Defense Industry Press,1991:190-216.(in Chinese)
[2]丘尔巴诺夫 E B.挤进时期内弹道学与挤进压力计算[M].杨敬荣,译.北京:国防工业出版社,1997:115-121. Qierbarov E B.Interior ballistics and engraving force calculation during engraving of projectile[M].YANG Jing-rong,translated. Beijing:National Defense Industry Press,1997:115-121.(in Chinese)
[3]孙河洋,马吉胜,李伟,等.坡膛结构变化对火炮内弹道性能影响的研究[J].兵工学报,2012,33(6):669-675. SUN He-yang,MA Ji-sheng,LIWei,et al.Study on influence of bore structure on gun's interior ballistic performances[J].Acta Armamentarii,2012,33(6):669-675.(in Chinese)
[4]段海涛,杜三明,张永振,等.高速干滑动条件下钢/铜摩擦副摩擦磨损表面摩擦热规律研究[J].润滑与密封,2007,32(10):40-42.DUAN Hai-tao,DU San-ming,ZHANG Yong-zhen,et al.Study on the friction heat rule under high-speed dry sliding conditions [J].Lubrication Engineering,2007,32(10):40-42.(in Chinese)
[5]樊黎霞,何湘玥.弹丸挤进过程的有限元模拟与分析[J].兵工学报,2011,32(8):963-968. FAN Li-xia,HE Xiang-yue.Finite element simulation and process analysis of projectile entering into barrel[J].Acta Armamentarii,2011,32(8):963-968.(in Chinese)
[6]殷军辉,郑坚,倪新华,等.弹丸膛内运动过程中弹带表层热软化机理分析[J].弹道学报,2012,24(2):106-110. YIN Jun-hui,ZHENG Jian,NIXin-hua,etal.Mechanism analysis of thermal softening of rotating band surface in process of projectilemotion in bore[J].Journal of Ballistics,2012,24(2):106-110.(in Chinese)
[7]李伟,马吉胜,孙河洋,等.弹丸惯性卡膛冲击问题动力学研究[J].振动与冲击,2011,30(5):161-163. LIWei,MA Ji-sheng,SUN He-yang,et al.Dynamic analysis for inertial bayonet-chamber process of a projectile[J].Journal of Vibration and Shock,2011,30(5):161-163.(in Chinese)
[8]万学仁.对定装式炮弹内弹道起始压力的分析讨论[J].弹箭与制导学报,1995,5(5):52-55. WAN Xue-ren.Analysis of initial pressure during the interior ballistics for conjoint ammunition[J].Journal of Projectiles,Rockets,Missiles and Guidance,1995,5(5):52-55.(in Chinese)
[9]林贵.弹带高速挤进膛线过程的模拟实验装置设计[D].南京:南京理工大学,2014:36-39. LIN Gui.Research the engraving processofband into riflingwith a high speed and experimental facility[D].Nanjing:Nanjing University of Science and Technology,2014:36-39.(in Chinese)
[10]马东方.基于空穴聚集的高应变率低应力三轴性拉伸断裂机理研究[D].宁波:宁波大学,2011:14-37. MA Dong-fang.A study for ductile fracture under high strain rate and low stress triaxiality tension based on void coalescence[D]. Ningbo:Ningbo University,2011:14-37.(in Chinese)
[11]Johnson G R,Cook W H.Fracture characteristics of threemetals subjected to various strains,strain rates,temperatures and pressures[J].Engineering Fractures Mechanics,1985,21(1):31-48.
[12]陈磊,周风华,汤铁钢.韧性金属圆环高速膨胀碎裂过程的有限元模拟[J].力学学报,2011,43(5):861-870. CHEN Lei,ZHOU Feng-hua,TANG Tie-gang.Finite element simulations of the high velocity expansion and fragmentation of ductilemetallic rings[J].Chinese Journal of Theoretical and Applied Mechanics,2011,43(5):861-870.(in Chinese)
[13]LiW Y,Wang F F.Modeling of continuous drive friction welding of mild steel[J].Materials Science and Engineering A,2011,528(18):5921-5926.
Simulation Study of Bearing Band Engraving Process and Interior Ballistic Process Based on Thermo-mechanical Coupling FEA Model
DING Chuan-jun,ZHANG Xiang-yan
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)
In order to study the dynamic interaction process of bearing band and barrel,a thermo-mechanical coupling finite element analysis(FEA)model is established.The engraving process of bearing band and interior ballistic process are simulated by the explicit finite elementmethod with the use of Fortran subroutines.The FEA model is proved to be effective by comparing the calculated resultswith experimental results.The calculated results show that the coefficient of secondary work varies as a function of time,and an extremum value appears in the early time when using classical interior ballistic equation. The thermal softening of bearing band surface has a significant effect on the interior ballistic process during the band engraving.For fixed cartridge case,the computational accuracy of the engraving process and the interior ballistic process could be improved by taking account of extracting bullet force.
ordnance science and technology;bearing band engraving;thermo-mechanical coupling;extracting bullet force;finite elementmethod
TJ410
A
1000-1093(2015)12-2254-08
10.3969/j.issn.1000-1093.2015.12.007
2015-01-31
江苏省自然科学基金项目(BK20140789);中央高校基本科研业务费专项项目(30915118826)
丁传俊(1986—),男,博士研究生。E-mail:381667117@qq.com;张相炎(1957—),男,教授,博士生导师。E-mail:xyzhang@mail.njust.edu.cn

