舰船混沌运动的单输入自适应变结构控制*

黄谦 李天伟 王书晓 李伟

(海军大连舰艇学院航海系，大连 116018)

舰船混沌运动的单输入自适应变结构控制*

黄谦†李天伟 王书晓 李伟

(海军大连舰艇学院航海系，大连 116018)

针对在舰船混沌运动控制中由模型不确定性及外部扰动无法确知所引起的控制结果无法保证的问题，采用自适应控制与滑模变结构控制相结合的方法，在设计切换函数时，将符号函数转移到控制输入的一阶导数当中，有效抑制了变结构控制中的抖振问题，并提出了一种单输入自适应滑模变结构控制方法．实验结果表明，与传统滑模变结构控制相比，新方法能够在系统模型具有不确定性及未知外部扰动的情况下实现舰船混沌运动的良好控制，为舰船混沌运动控制提供了一种可靠的工程实现途径．

船舶混沌运动， 模型不确定性， 单输入控制， 自适应控制， 滑模变结构控制

引言

随着海军新型舰艇的陆续服役以及舰载武器装备的更新，舰船航行安全保障、舰载机的安全起降以及新型武器装备的作战使用等军事应用领域对舰船的航行运动控制提出了更高的要求．通过将混沌理论引入舰船的非线性运动的研究之中发现，舰船在航行过程中产生的非线性混沌运动是导致其无法保持直航向航行的重要因素．舰船的混沌运动容易导致失控或偏离航向，同时也对舰载武器系统的作战使用和特种舱面作业产生各种不利影响，严重时甚至危及舰船自身安全［1，2］．

国内外学者对舰船航行混沌运动进行了大量的研究，并就舰船混沌运动的控制进行了有益的尝试和探索．张显库［3］提出利用精确反馈线性化和闭环增益成形算法相结合的非线性简捷控制方法进行船舶横摇运动的混沌控制，取得了较好的效果．本文作者曾经探讨了一种利用基于Melnikov方法的周期矩形脉冲参量微扰控制方法［4］，实现了将舰船混沌运动快速稳定到周期轨道的目的，但对于将系统状态变量稳定控制到不动点，该方法依然存在不足．李天伟［5］基于Lyapunov稳定性理论提出了一种简化自适应控制方法，方法易于实现、效果较好，但该方法必须在系统部分参数已知的情况下才可以实现舰船混沌运动的控制，具有局限性．孔昭毅［6］针对一个新混沌系统研究了自适应滑模变结构控制方法，实现了将混沌系统稳定到平衡点的目的，但是，对于变结构控制中存在的抖振问题则没有进行研究和消除，控制器的工程实现存在一定问题．

为了解决舰船混沌运动实际控制过程中由于模型不确定性及外部扰动无法确知所引起的控制结果无法保证的问题，本文将自适应控制理论与滑模变结构控制方法相结合形成了舰船混沌运动的自适应滑模变结构控制．同时，为了抑制变结构控制中的抖振问题并满足工程实现的需要，采用了具有实际意义的单输入控制方案，提出了一种舰船混沌运动的单输入自适应滑模变结构控制方法，实现了舰船混沌运动的稳定控制．

1 混沌系统模型与问题描述

考虑文献［7］中的舰船转首操纵运动非线性响应模型，建立舰船转首操纵运动非线性响应混沌模型［4］如下:

其中，x=［x1，x2］T∈R2，y∈R 分别为系统状态变量及输出量，x1=y 为舰船转首角速度;a，b，c，d，e，ω为系统参数．研究发现，当船的阻尼项系数和刚度项系数相差不是很大时，通过反馈增量的补偿，阻尼项系数和刚度项系数是同一数量级，系统将进入非线性混沌状态，即舰船在航向保持过程中会出现混沌现象［4］．

为了验证模型的混沌特性，本文以某型军用船舶为研究对象，计算得到其相应系统参a=－0．3208、b=0．2715、c= －4．3945、d=0．10368、e=0．0788、ω=0．8，则该船的运动非线性模型如下:

用Matlab/Simulink软件进行数值仿真实验，采用四阶Runge－Kutta方法，仿真步长取为s，初始值取为(x0，y0)=(0，0)，仿真运行 2000s，去除前400s的暂态数据，绘制出系统相位图及Poincaré截面映射图，如图1、图2所示．

图1 系统相位图和Poincaré映射图Fig．1 phase and Poincaré map of system

根据图1可以知道，该型船的转首操纵运动非线性模型具有明显的混沌特性，因此，必须对此时的舰船混沌运动进行控制，目的是使得舰船转首角速度x1稳定至零，以保证舰船航行安全及特种作业任务的完成．而海上航行的舰船是在复杂环境中运动的，其在运动过程中受到多种外力的扰动，导致其运动模型具有某种程度上的不确定性．同时，大量研究实践表明，由于控制对象的复杂程度日渐增加，并且其运行环境又因时而异，因此用精确的数学模型描述这些系统的动态特性是不现实的，甚至是不可能的．这就使得在进行控制系统设计时，不可避免地会遇到不确定性模型［8］．对于海上舰船运动而言，考虑到模型中的参数不确定性及受到的未知外部扰动影响，舰船转首操纵运动非线性响应混沌模型可写为如下形式:

其中，Δf(x，t)∈R为模型不确定项，Δd(t)∈R为未知的外部扰动．

2 舰船混沌运动的自适应滑模变结构控制

在实际的控制工程中，系统参数往往带有不确定性而导致了系统不确定项Δf(x，t)的出现，同时由于系统受到的外部扰动Δd(t)未知，此时采用基于上界的滑模变结构控制方法，在设计变结构控制器时必须要保证切换项增益η大于扰动上界，否则往往无法取得较好的控制结果，而较大的切换项增益往往会加剧系统的抖振现象［9］．

为了解决实际控制过程中由于模型不确定性及外部扰动无法确知所引起的控制结果无法保证的问题，需要对模型不确定性及外部扰动边界进行估计．因此，本文在进行合理假设的基础上，根据Lyapunov稳定性理论，提出了一种具有鲁棒性的自适应滑模变结构控制器．

假设1 混沌系统状态轨迹的全局有界导致了不规则吸引子［10］，因此，假设式(3)所示系统等号右端是耗散的，也即在相空间中是有界的．在此基础上，假设模型不确定项Δf(x，t)及其一阶导数Δ(x，t)是有界的．也就是说，存在大于零的未知正常数α与β，有:

假设2 假设系统所受外部扰动Δd(t)及其一阶导数Δ是有界的，也即有:

其中，δ、ε为未知正常数．

由于在传统滑模变结构中，符号函数包含于控制律中，并伴随着抖振现象的发生．为了抑制抖振现象，受到文献［12］的启发，经过大量试验与分析，本文考虑将非平稳的符号函数从输入控制u(t)中转移到控制输入的一阶导数u(t)当中，并按照此思路，对传统滑模变结构控制中的切换函数进行改进，构造新的切换函数s为如下形式:

定理1 考虑如公式(3)所示的具有模型不确定性且受到外部扰动的受控混沌系统，有假设1与假设2成立，受控系统滑模面s取式(6)，自适应动态控制律取为如下形式:

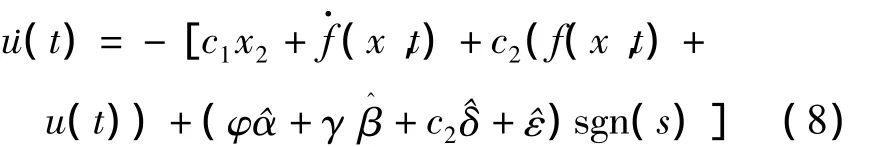
其中，c1、c2为需要选取的切换函数参数．当系统进入滑模后，状态轨迹保持在切换面上，满足s=0且s=0，即有:

自适应律取为:

其中，分别为边界值 α、β、δ、ε的估计值．此时，系统的混沌状态得到抑制，系统输出渐近稳定至零点，且系统的平衡状态是全局渐近稳定的．

证明:

对公式(3)所示系统，取其Lyapunov函数V为:

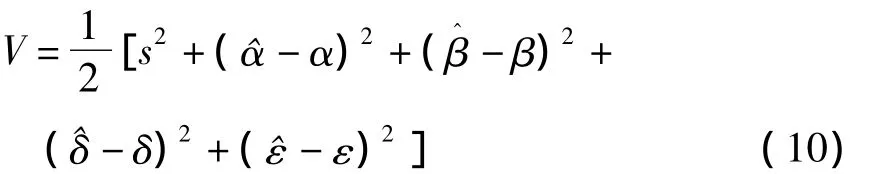
对Lyapunov函数进行求导，有:

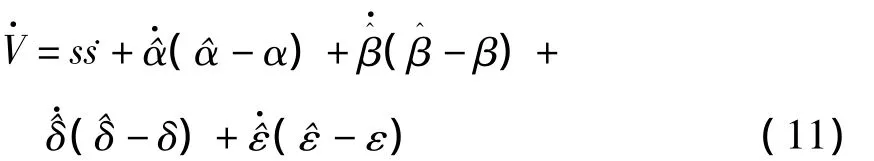
代入所设计的滑模面s及其时间导数s，则有:

根据假设1及假设2，可得:

将自适应动态控制律(8)代入，则有:

取自适应律如式(9)所示，则变为:

式中，h(t)=|s|［(φ －c2)α +(γ －1)β］≥0，对式(16)从0到t进行积分，则有:

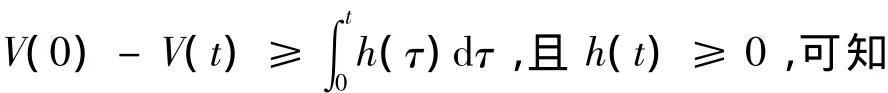
综合以上假设1、2及定理1可知，在自适应变结构控制器u(t)的作用下，系统(3)中的混沌状态将得到抑制，且系统的输出能渐近稳定到零点，此时，闭环受控系统的平衡状态是全局渐近稳定的．定理1证明完毕．

由于(φ－c2)α+(γ－1)β＞0，因此，可得

3 控制实验仿真及分析

对于如式(12)所示的舰船转首操纵运动非线性混沌模型，为了验证定理1所提出的控制器的正确性和有效性，对控制器的控制作用进行仿真实验和分析．用Matlab/Simulink软件进行仿真实验，采用四阶Runge－Kutta方法，系统参数取a=－0．3208、b=0．2715、c= －4．3945、d=0．10368、e=0．0788、ω =0．8，按照式(3)所示，假设由于系统参数不确定而产生的模型不确定项Δf(x，t)如式(19)所示:

系统受到的不确定扰动为Δd(t)=0．02cost．

图2 系统相位图和Lyapunov指数谱Fig．2 Phase and Lyapunov exponents of system

首先对具有模型不确定性且受到外部扰动的舰船转首操纵运动进行仿真，观察其运动特性．仿真时选取舰船转首操纵运动非线性响应混沌模型的初始值为(x10，x20)=(0，0)，仿真步长为 0．001s，仿真时长为．如图2所示分别为系统相图及系统Lyapunov指数谱图．由图2可知，系统吸引子轨线是反复折叠和相互交叉而形成的密集的带，并不是简单的闭曲线，系统吸引子为奇怪吸引子，而具有奇怪吸引子的运动就是混沌的［13］．另外，由图可知，系统最大Lyapunov指数λ1=0．1045，系统运动呈现明显的混沌特征．综合以上分析可以知道，具有模型不确定性且受到外部扰动的舰船转首操纵运动在不施加控制作用时依然可能具有明显的混沌动力学特性．

为了验证本文所提方法的有效性与优越性，将本文方法与传统变结构控制方法一起进行实验比较．由于传统方法在进行滑模变结构控制器设计时，需要知道不确定扰动的上界才能进行变结构控制器的设计，因此在进行传统控制器设计时，假设模型不确定项f(x，t)和不确定扰动d(t)上界已知．依据定理1设计自适应滑模变结构控制器，取滑模变结构控制器参数 c1=c2=5，φ =5．5，r=1．2，设定舰船初始航向为045°．0，选择在t=40s时刻加入自适应滑模变结构控制作用，考察控制结果．

图3 单输入自适应滑模变结构控制Fig．3 Single input adaptive sliding mode control

如图3所示即为本文所提方法的系统控制结果，根据仿真实验结果，从图3(c)中可以看出，在系统进入混沌状态后，舰船航向无法稳定保持在设定航向之上，而是根据图3(a)所示的舰船转首角速度x1做来回振荡运动．在系统加入本文所设计的自适应滑模变结构控制作用后，由图3(a)－(c)可知，系统状态变量x1及x2都能够被迅速稳定到零点，舰船转首操纵运动中的混沌状态得到了有效抑制，舰船航向也能够被迅速稳定到045°．0的设定航向上，实现了舰船航向的稳定控制．同时，从图3(d)、(e)中可以看到，由于采用了重新设计的切换函数，并且将符号函数转移到控制作用u(t)的一阶导数u(t)之中，有效抑制了传统变结构控制中的抖振现象，保证了系统的稳定性和变结构控制的实用性，易于实际工程设计及实现．

而与本文所提方法相比，采用同样的模型参数设置，运用传统变结构控制方法进行控制，得到系统滑模面s及控制输入u(t)时序图，如图4(a)、(b)所示，可以发现，传统滑模变结构控制方法在舰船混沌运动控制中系统滑模面s存在明显的抖振现象，系统的控制输入u(t)更是如此，这给整个控制器的工程实现带来了极大的困难．而且在设计变结构控制器时，传统方法必须要保证切换项增益大于外部扰动上界，否则往往无法取得较好的控制结果．

图4 传统滑模变结构控制Fig．4 Figure of tradition sliding mode control

综合以上控制实验可知，采用本文所提方法设计的自适应滑模变结构控制器，很好地解决了实际控制过程中由于模型的不确定性以及外部扰动无法确知所引起的控制结果无法保证的问题，对具有模型不确定性且受到外部扰动的舰船混沌运动具有良好的抑制作用，能够使得系统的状态输出被稳定至不动点，确保了对舰船混沌运动的有效控制．

4 结论

针对具有模型不确定性且受到外部扰动的舰船非线性混沌运动的控制问题，将自适应控制理论与滑模变结构控制方法相结合，提出了一种具有良好应用价值的舰船混沌运动单输入自适应滑模变结构控制方法．根据混沌系统轨迹的全局有界性，该方法采用自适应控制技术对舰船转首操纵运动的模型不确定性及未知外部扰动的边界进行了合理估计，同时，利用动态滑模面技术，将滑模变结构控制中的符号函数转移至系统控制输入量的一阶导数之中，避免了滑模变结构控制中的抖振问题，并通过Lyapunov稳定性理论证明了其鲁棒性．该方法实现了将混沌系统输出变量控制到零点上的目的，保证了舰船航向的稳定性，具有良好的滑模控制性能．仿真实验结果表明，与传统自适应控制方法相比较，新方法能够在系统模型具有不确定性及未知外部扰动的情况下实现舰船混沌运动的良好控制，对实现舰船混沌运动的稳定控制具有重要的实践意义，为舰船航向的稳定控制提供了一种可靠的实现途径．

1 黄谦，李天伟，杨绍清．船舶航行数据的相空间重构及混沌特性分析．计算机应用，2011，31(11):3157～3164(Huang Q，Li T W，Yang S Q．Analysis on phase space reconstruction and chaotic dynamic characteristic of ship＇s sailing data．Journal of Computer Applications，2011，31(11):3157～3164(in Chinese))

2 侯建军，常小勇，石爱国．舰船摇荡运动数据采集及混沌特性分析．船舶工程，2011，33(6):25～28(Hou J J，Chang X Y，Shi A G．Data collection and chaotic characteristic analysis of ship swaying motions．Ship Engineering，2011，33(6):25～28(in Chinese))

3 张显库，王坤飞．船舶横摇运动中的混沌及其非线性简捷控制．中国造船，2010，51(4):21～27(Zhang X K，Wang K F．Chaos of ships rolling motions and its nonlinear simple and direct control．Shipbuilding of China，2010，51(4):21～27(in Chinese))

4 黄谦，李天伟，杨绍清．船舶混沌运动的周期脉冲参数微扰控制．控制理论与应用，2012，29(12):1603～1608(Huang Q，Li T W，Yang S Q．Periodic impulsive parameter perturbations control for chaotic ship steering．Control Theory＆Applications，2012，29(12):1603～1608(in Chinese))

5 李天伟，黄谦，李正友．一种有效的船舶混沌运动自适应控制方法．舰船科学技术，2013，35(10):29～32(Li T W，Huang Q，Li Z Y．A valid adaptive control method for chaotic ship steering．Ship Science and Technology，2013，35(10):29～32(in Chinese))

6 孔昭毅．一个新混沌系统的自适应滑模变结构控制．动力学与控制学报，2013，11(2):114～117(Kong Z Y．Adaptive sliding mode variable structure control of a new chaotic system．Journal of Dynamics and Control，2013，11(2):114～117(in Chinese))

7 李殿璞．船舶运动与建模(第2版)．北京:国防工业出版社，2008:40～49(Li D P．Ship motion and modeling(Second Edition)．Beijing:National Defend Industy Press，2008:40～49(in Chinese))

8 庄开宇．变结构控制理论若干问题研究及其应用［博士学位论文］．杭州:浙江大学，2002(Zhuang K Y．The study and application of variable structure control theory［PhD Thesis］．Hangzhou:Zhejiang University，2002(in Chinese))

9 陈志梅，王贞艳，张井岗．滑模变结构控制理论及应用．北京:电子工业出版社，2012:10～13(Chen Z M，Wang Z Y，Zhang J G．Sliding mode variable structure control theory and application．Beijing:Publishing House of Electronics Industry，2012:10～13(in Chinese))

10 Fradkov A L，Evans R J．Control of chaos:methods and application in engineering．Annual Reviews in Control，2005(29):33～56

11 Li H，Liao X，Li C，et al．Chaos control and synchronization via a novel chatter free sliding mode control strategy．Neurocomputing，2011(17):3212～3222

12 关巍．基于Backstepping的船舶运动非线性自适应鲁棒控制［博士学位论文］．大连:大连海事大学，2010(Guang W．The nonlinear adaptive backstepping robust control for ship motion［PhD Thesis］．Dalian:Dalian Maritime University，2010(in Chinese))

13 吕金虎，陆君安，陈士华．混沌时间序列分析及其应用．武汉:武汉大学出版社，2002(Lv J H，Lu J A，Chen S H．Analysis on chaotic time series and its application．Wuhan:Wuhan University Press，2002(in Chinese ))

*The project supported by the Natural Science Foundation of China(60572160，61303192)，Scientific Research Development Foundation of Dalian Naval Academy

† Corresponding author E－mail:finalfanst@163．com

CHAOS CONTROL OF SHIP STEERING VIA SINGLE INPUT ADAPTIVE SLIDING MODE CONTROL METHOD*

Huang Qian†Li Tianwei Wang Shuxiao Li Wei
(Department of Navigation，Dalian Naval Academy，Dalian116018，China)

Aiming at the uncertainty problem caused by model uncertainties and external disturbances in actual control process of chaotic ship steering，this paper combined the adaptive control method with sliding mode control method，and also transferred the sign function to the first derivative of control input when designing the switching function，which eliminates the chattering problem in common sliding mode control method，so a single input adaptive sliding mode control method for chaotic ship steering control was proposed．The experiment results show that，compared with the traditional sliding mode control method，the proposed method has a good performance on chaotic ship steering control with model uncertainties and external disturbances，which provides a more reliable way for chaotic ship steering control．

chaotic ship steering， model uncertainty， single input control， adaptive control， sliding mode control

9 June 2014，

2 October 2014．

10．6052/1672－6553－2014－082

2014－06－09 收到第 1 稿，2014－10－02 收到修改稿．

*国家自然科学基金资助项目(60572160，61303192)和海军大连舰艇学院科研发展基金资助项目

E－mail:finalfanst@163．com