非扩张映射的公共最佳逼近点问题
隋林林,肖 松
(哈尔滨师范大学)
1 引言及预备知识
最佳逼近点理论的研究源于对不动点理论的研究.1969 年,Ky Fan[1]在 Tvchonoff[6]不动点定理的基础上,提出了经典的最佳逼近点定理.
定理1.1[1]设X是赋范线性空间E中的非空紧凸子集,映射T:X→E是连续映射.则存在y0∈X,使得

对于非线性规划问题

不一定能找到最优解x.使得d(x,Tx)的误差达到全局最小值.
事实上,若A,B是度量空间(X,d)中的非空子集,对于任意的x∈A,Tx∈B,一定有d(x,Tx)≥d(A,B).如果存在x*满足条件d(x*,Tx*)=d(A,B),则x*是这个非线性规划问题的解.因此,x*是最佳逼近点.
定义1.1 设A,B是度量空间(X,d)中的非空子集,设映射T:A→B,若存在x*∈A,使得d(x*,Tx*)=d(A,B),则称x*为T的最佳逼近点.
在不动点理论的研究中,具有压缩条件的映射的不动点定理一直扮演着很重要的角色.它最初起源于1922年Banach提出的压缩影像原理.他指出完备度量空间中每个压缩映射都有唯一不动点.之后,一些学者对Banach压缩映射原理进行了推广.其中,在2003年,Kirk[2]等人提出了以下结论.
定理1.2[2]设A,B是完备度量空间X中的非空子集,映射T:A∪B→A∪B满足T(A)⊆B,T(B)⊆A.若对任意的x∈A,y∈B,α∈(0,1),有

则A∩B≠∅,T在A∩B中有唯一不动点.
上述结论中,当α=1时,压缩映射变为非扩张映射.
定义1.2 设(X,d)是距离空间,映射T:X→X.若对任意的x,y∈X,有d(Tx,Ty)≤d(x,y),则称T是X上的非扩张映射.
2005 年,Eldred,Kirk和Veeramani[3]推广了Milman和Brodskii[4]所提出的正规结构,给出了逼近正规结构的概念.
定义1.3[3]设在Banach空间中的凸集对(K1,K2)具有逼近正规结构是指:对任意的有界闭凸逼近对(H1,H2)⊆ (K1,K2),若d(H1,H2)=d(K1,K2),并且δ(H1,H2)>d(K1,K2),则一定存在(x1,x2)∈H1×H2,使得
δ(x1,H2)<δ(H1,H2),δ(x2,H1)<δ(H1,H2)
定理1.3[3]设(A,B)是 Banach 空间中的非空弱紧凸对,(A,B)具有逼近正规结构.若映射T:A∪B→A∪B满足下列条件:
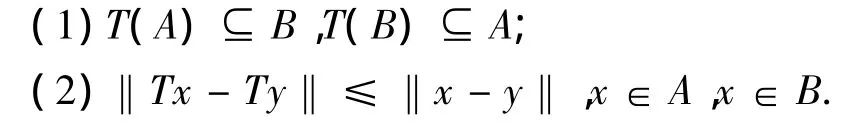
则存在(x,y)∈A×B,使得

2009 年,A.Thagafi和 Shahzad[5]引进了一种新的压缩映射,叫做循环φ-压缩映射.并给出了循环φ-压缩映射的最佳逼近点定理.
定义1.4[5]设A,B是度量空间X中的非空子集,映射T:A∪B→A∪B满足T(A)⊆B,T(B)⊆A.若存在严格增的函数φ:[0,+∞)→[0,+∞)使得
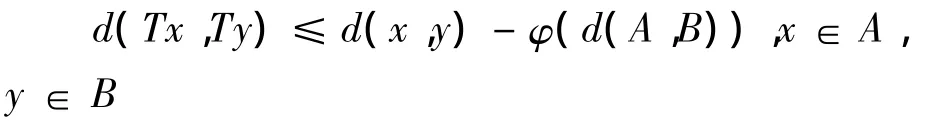
则称T是循环φ-压缩映射.
定理1.4[5]设A,B是一致凸的Banach空间X中的非空子集,A是闭凸集,T:A∪B→A∪B是循环φ-压缩映射.若对于x0∈A,定义xn+1=Txn,n=0,1,2,…,则存在x∈A,使得x2n→x,T2x=x,并且d(x,Tx)=d(A,B).
2011年,Sankar[7]在P-性质的条件下证明出对于一个弱压缩映射存在最佳逼近点.2012 年,Abkar和 Gabeleh[8]基于 Sankar的理论,证明了在一个非扩张映射下的最佳逼近点问题.
上述所研究的是一个映射的最佳逼近点问题,下面考虑,是否存在两个映射的公共最佳逼近点.设A,B是度量空间(X,d)中的非空子集,S:A→B和T:A→B为非自身映射,那么方程Sx=x和Tx=x不一定有公共解,即映射S和T不一定存在公共不动点.因此,在公共解不存在的情况下,将尝试找到一个x,使得在某种条件下,d(Sx,x)与d(Tx,x)的误差同时达到全局最小值.对于两个非自身映射来说,考虑公共最佳逼近点问题.
定义 1.5[9]设A,B是度量空间(X,d)中的非空子集,映射S:A→B和T:A→B为非自身映射.若对∀x∈A满足d(x,Sx)=d(x,Tx)=d(A,B),则称x是映射S和T的公共最佳逼近点.
显然,若映射为自身映射,则公共最佳逼近点为公共不动点.
2012年,Basha[9]在度量空间中通过给出交换逼近和能被逼近地交换的定义,且存在非负实数 α<1,有d(Sx1,Sx2)≤ αd(Tx1,Tx2),∀x1,x2∈A的情况下,证明出了公共最佳逼近点的存在.同年,Gabeleh[11]在集合具有P-性质的条件下,将Basha论文中的“能被逼近地交换和逼近紧”的条件弱化,进而证明出存在公共最佳逼近点.
下面给出该文所涉及的相关定义及结论.
设A,B是度量空间(X,d)中的非空子集,定义:

定义1.6 设A是线性空间X中的非空子集.若存在点p∈A,使得对任意的x∈A,α∈[0,1],有

则称集合A为星形集.点p为A的中心.
定义1.7[10]设A,B是度量空间(X,d)中的非空子集,若对任意的x,u,v∈A,映射S:A→B和T:A→B满足以下条件:
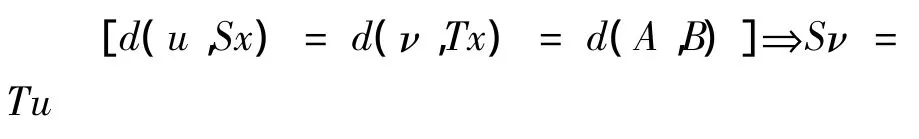
则称S,T为交换逼近的.
定义1.8[10]设A,B是度量空间(X,d)中的非空子集,若对任意的u,ν∈A,y∈B,映射S:A→B和T:A→B满足以下条件:

则称S,T能被逼近地交换.
定义 1.9[7]设(A,B)是度量空间(X,d)中非空子集对,其中A0非空,对于x1,x2∈A0,y1,y2∈B0,有

则称非空闭子集对(A,B)具有p-性质.
显然,对于X中任意非空子集A,(A,A)有p-性质.
定义1.10[12]设A,B为赋范线性空间中的非空凸子集,若对任意的x,y∈A或者x,y∈B,存在λ∈(0,1),有

则称映射T:A→B为仿射映射.
定理1.5[13]设A,B是Banach空间中分别以p,q为中心的星形集,‖p-q‖=d(A,B).则A0,B0分别是以p,q为中心的星形集.
定理1.6[10]设A,B是完备度量空间X中的非空闭子集.A关于B是逼近紧集.若A0,B0非空,且非自身映射S:A→B和T:A→B满足以下条件:
(a)存在非负的实数α<1,有d(Sx1,Sx2)≤ αd(Tx1,Tx2),∀x1,x2∈A.
(b)映射T是连续的.
(c)S,T是逼近交换映射.
(d)S,T能被逼近地交换.
(e)S(A0)⊆B0,S(A0)⊆T(A0).则存在一个元素x∈A,使得

进而,若x*是映射S,T的另一个公共最佳逼近点,则有d(x,x*)≤2d(A,B).
定理1.7[11]设(A,B)是完备度量空间X中的非空闭子集对.假设A0为非空集,非空闭子集对(A,B)具有P-性质,且非自身映射S:A→B和T:A→B满足以下条件.
(a)存在非负的实数α<1,有d(Sx1,Sx2)≤ αd(Tx1,Tx2),∀x1,x2∈A.
(b)映射S,T是连续的.
(c)S,T是逼近交换映射.
(d)S(A0)⊆B0,S(A0)⊆T(A0).则映射S,T存在公共最佳逼近点.
该文主要在上述定理的基础上,考虑紧的星形集上当“α=1”的情况下,公共最佳逼近点的存在性问题.
2 主要结论
定理2.1 设A,B是Banach空间X中分别以p,q为中心的星形集,‖p-q‖ =dist(A,B).映射S:A→B和T:A→B是非自身映射,若(A,B)具有P-性质,A是紧集,且满足以下条件:
(a)d(Sx1,Sx2)≤d(Tx1,Tx2),∀x1,x2∈A.
(b)映射S,T是连续的.
(c)S,T是逼近交换映射.
(d)S(A0)⊆B0,S(A0)⊆T(A0).
(e)T是仿射,Tp=q.则存在元素x∈A,使得

证明 由于A,B是Banach空间中分别以p,q为中心的星形集,‖p-q‖ =dist(A,B).则由定理1.5知,A0,B0是分别以p,q为中心的星形集.
对任意正整数k≥1,作映射Sk:A→B,其中
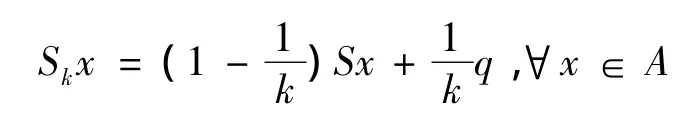
则有Sk(A0)⊆B0,且对于任意的x,y∈A0,有

事实上,对于 ∀x∈A0,Skx∈Sk(A0),又S(A0)⊆B0,则有Sx∈B0,由B0是q-星形集,则有
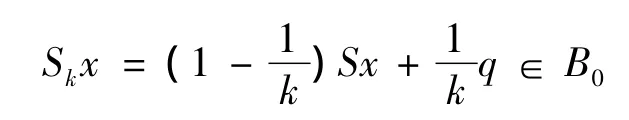
即Sk(A0)⊆B0.
对于 ∀x,y∈A0,‖Skx-Sky‖

由S和T是逼近交换的,则对于任意的u,ν,x∈A,‖u-Sx‖ = ‖ν-Tx‖=d(A,B),有Sν=Tu.
下面证明,若任意的uk∈A及ν满足:‖ν-Tx‖ = ‖uk-Skx‖=d(A,B),则有Skv=Tuk成立.
事实上,由

d(A,B).所以有
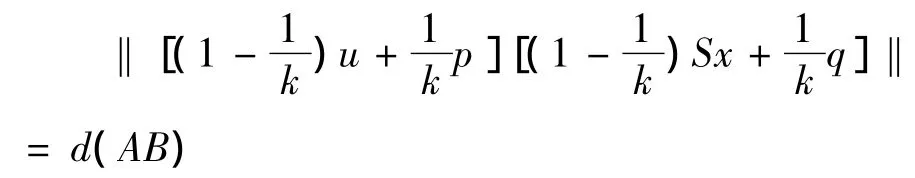
由P-性质可知
又因为T是仿射的,所以有

这就证明了T与Sk是逼近交换的.
由定理1.7可知,对于每个k≥1,在A中均存在公共最佳逼近点.
即对于每个k≥1,存在唯一的uk∈A0,使得
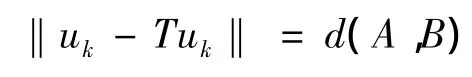
且 ‖uk-Skuk‖=d(A,B)
又因为 ‖uk-Suk‖ =‖uk-Skuk+Skuk-Suk‖
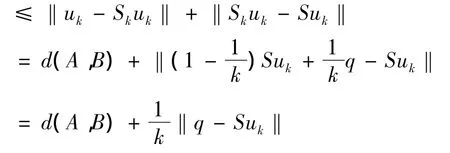
容易知道,存在正整数m,由于q∈B0,uk∈A0,所以Suk∈B0,由于A具有紧性,所以A0⊂A是有界的,从而B0是有界的,且有
d(A0,B0)=d(A,B),则有

所以当k→∞时,→0.则‖uk-Suk‖ →d(A,B).
由于A具有紧性,则在A中存在收敛子列{un},不妨设un→u0∈A,(n→∞).由于S和T是连续的.则有Sun→Su0,Tun→Tu0∈B,(n→∞).从而有
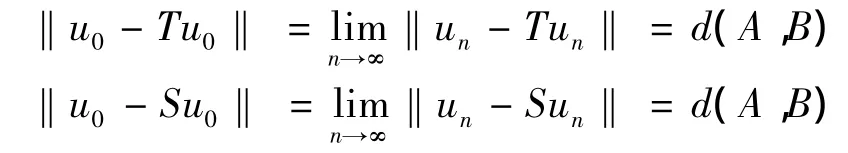
则 ‖u0-Tu0‖=d(A,B)

即存在公共最佳逼近点.且当A0=B0时,公共最佳逼近点变为公共不动点.
3 结束语
该文主要研究了具有P-性质的紧的星形集上两个连续逼近交换仿射映射,当“α=1”的情形下的公共最佳逼近点的存在性问题,推广了已有结论.
[1] Ky Fan.Extensions of two fixed point theorems of Browder[M].Math Z,1935,112:234-240.
[2] Kirk W A,Srinivasan P S,Veeramani P.Fixed points for mappings satifying cyclical contrative conditions[J].Fixed Point Theor,2003(4):79-89.
[3] Eldred A A,Kirk W A,Veeramani P.Proximal normal structure and relatively nonexpansive mappings[J].Studia Math,2005,171(3):283-293.
[4] Milman D P,Brodskii M S.On the center of a convex set[J].Dokl Nauk SSSR(N.S),1948,59:837-840.
[5] Al-Thagafi M A,Shahzad N.Convergence and existence results for best proximity points[J].Nonlinear Anal,2009,70(10):3665-3671.
[6] Tvchonoff A.Ein fixpunktsatz[M].Math Ann,1935,111:767-776.
[7] Sankar V.A best proximity point theorem for weakly contractive non-self mappings[J].Nonl Anal,2011,74:4804-4808.
[8] Abkar A,Gabeleh M.Best proximity points of non-self mapping[J].Topo,2012.
[9] Mongkolkeha C,Kumam P.Some common best proximity points for proximity commuting mappings[J].Optim,2012:275-284.
[10] Basha S S,Common best proximity points:global minimization of multi-objective functions[J].J Glob Optim,2012:367-373.
[11] Gabeleh M.Best proximity points for weak proximal contractions[J].Msc,2012.
[12] Eldred A A,Raj V S,Veeramani P.On best proximity pair theorem for relatively U-continuous mappings[J].Nonlinear Analysis,2011,74:3807-3875.
[13]姬玉婷.相对非扩张映射的最佳逼近点问题[D].哈尔滨师范大学硕士学位论文,2014.

