例谈初中数学课堂学生主体性实施

王宇峰++朱宸材

新课标的要求，在课堂教学中力求使学生的“主体”地位得以充分地体现，要打破传统教学过程中教师是“主角”，少数学习好的学生是“配角”，更多的学生充其量是陪衬的“演员”，甚至是观众或听众的弊端，使更多的学生成为学习的主体，能给全体学生上台“表演”的机会，集中精力，均有收获。教师通过课堂互动的模式调动学生的思维，学生积极参与其中探究问题，解决问题。

一、创设合理问题情境，激发学生主动探索

苏霍姆林斯基说过：“如果学生没有学习的愿望，我们所有的计划、所有的探索和理论传统都会落空。”而思维永远是由问题开始的。课堂中，教师以创设情境为主线，根据教材的特点和学生的具体学情，把学生引入一种与问题有关的情境中去，让学生通过观察，不断积累知识，激发学生的探究兴趣。

【案例1】例如，在进行《反比例函数的应用》教学时，笔者设计了这样一个情境：某校科技小组进行野外考察，途中遇到一片湿地，为了安全迅速通过，铺垫了若干块木板，构建成一条临时通道，从而顺利完成任务。

思考：①你能解释他们这样做的道理吗？②当人和木板对湿地的压力一定时，随着木板面积S（m2）的变化，人和地板对地面的压强P（Pa）将如何变化？

结合问题情境提供的背景，出示题目：如果人和木板对湿地地面的压力合计600N，那么①用含S的代数式表示P，P是S的反比例函数吗？为什么？②在直角坐标系中，作出相应的函数图像。③利用图像对②、③作出直观解释，并与同伴进行交流。

【评析】设计这一情境既为下一步的教学内容提供背景材料，又激发起学生的好奇心，带着对数学的求知欲，进入设计的知识问题串，引导学生讨论探究。

二、设计自主探究环节，指导学生发现规律

数学课程标准倡导自主探究的学习方式。学生是学习的主体，教师的责任在于提供各种学习条件，给予点拨激励唤起他们发自内心的学习愿望。自主探究是自主学习的前提基础。学生主要通过观察、实验，体会变化，主动参与发现规律。教师在课堂教学过程中，教学目标的确定、教学过程的设计、教学方法的选用等，都从学生实际出发。在课堂上最大限度让学生动口、动脑，极大地调动学生学习的主动性，促进学生主动参与、主动思考、主动实践。

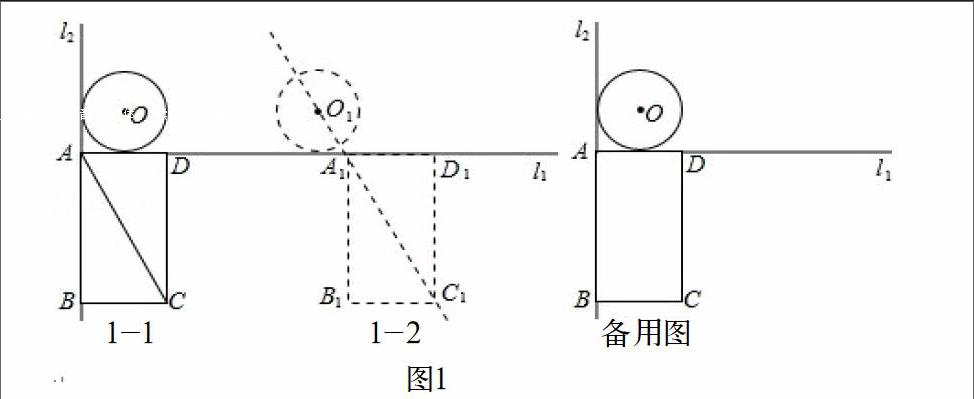
【案例2】在初三中考专题《图形的运动》复习教学时，笔者曾经给学生出了这样一道题：如图1，已知l1⊥l2，⊙O与l1，l2都相切，⊙O的半径为2cm，矩形ABCD的边AD、AB分别与l1，l2重合，AB=4cm，AD=4cm，若⊙O与矩形ABCD沿l1同时向右移动，⊙O的移动速度为4cm/s，矩形ABCD的移动速度为6cm/s，设移动时间为t（s）。

（1）如图1-1，连接OA、AC，则∠OAC的度数为 ；

（2）如图1-2，两个图形移动一段时间后，⊙O到达⊙O1的位置，矩形ABCD到达A1B1C1D1的位置，此时点O1，A1，C1恰好在同一直线上，求圆心O移动的距离（即OO1的长）；

（3）在移动过程中，圆心O到矩形对角线AC所在直线的距离在不断变化，设该距离为d（cm），当d<2时，求t的取值范围。

首先，通过连接OA、AC，利用三角函数的知识得到第一问的答案∠OAC的度数为105°。接着，在进行第二问的探究时，引导学生画出⊙O和矩形ABCD的示意图（如图2位置二）。提示学生根据条件入手发现图形中隐含的数量关系，学生通过摸索构造出Rt△A1D1C1和Rt△A1O1E，利用三角函数算出A1E的距离。然后利用图形追击的知识得到：A1E=AA1﹣OO1﹣2=2t﹣2，最后算出t=+1，从而得到圆心O移动距离。讲解第三问时，由于有了第二问的基础，学生探究的积极性被极大地调动出来，主动画出圆O与直线AC相切时的情况（如图2位置一和位置三）类比第二问求解方法学生比较容易找到答案。通过这样的探究模式，可以让学生克服碰到数学综合题的恐惧心理，增强学生学习的信心。

三、鼓励小组合作交流，促进学生完善知识

在传统的学习环境中，虽然几十个人在一个教室里学习，但学习方式却是个体的、封闭的，听课、理解、做作业、考试，除了与教师的单线联系之外，缺少横向的、与同学之间的沟通。这种环境和学习方式，容易让学生产生枯燥，厌倦的情绪。因此，在教学中我尽量给学生讨论、分析的机会，使学生在知识方面相互补充，在学习方法上相互借鉴，同时要求小组成员之间相互尊重，畅所欲言，既要表达自己的观点，也要虚心听取别人的意见、想法，相互交流，取长补短，学会与同学合作，正确评价他人与自己。

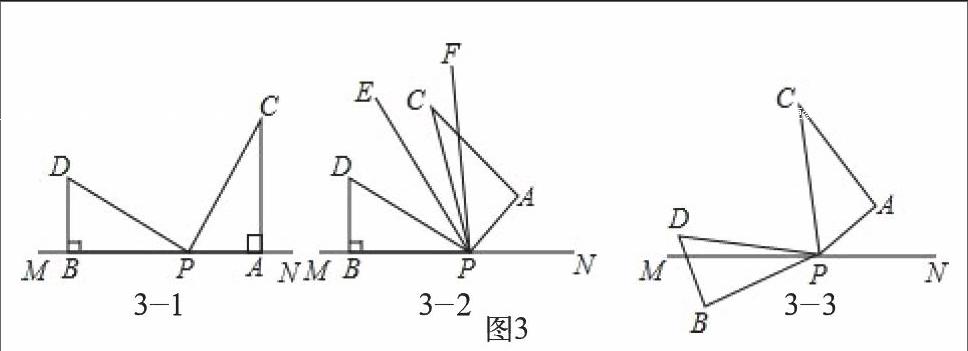
【案例3】在《角的和差关系》复习时，我给学生出了这样一道题目：如图3，两个形状、大小完全相同的含有30。、60。的三角板如图3-1放置，PA、PB与直线MN重合，且三角板PAC，三角板PBD均可以绕点P逆时针旋转。

（1）试说明：∠DPC=90。；

（2）如图3-2，若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度，PF平分∠APD，PE平分∠CPD，求∠EPF；

（3）如图3-3，若三角板PAC的边PA从PN处开始绕点P逆时针旋转，转速为3。/秒，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速为2。/秒，在两个三角板旋转过程中（PC转到与PM重合时，两三角板都停止转动），以下两个结论：① 为定值；②∠BPN+∠CPD为定值，请选出正确的结论，并说明理由。

【评析】这是一道有关三角形运动中的动线问题，主要隐含了角度和差的关系。初一的学生由于刚接触几何，对这样一类问题都会感到很困惑，为了让学生更好掌握线运动的规律，我将全班学生分成六个小组，每组选择一个思维较为活跃的学生作为组长，然后，让组长带领组员共同探索这道题，探索完成后，每一个小组派一名代表上台讲解这道题的思路，如果答对该小组将会有奖励，如果打错该小组将失去答题机会，换成其他小组来答题。第一问和第二问学生很快完成，在解答第三问时，小组成员有了不同的意见，有学生认为∠BPN+∠CPD为定值，这是笔者指导小组长让组员把每一种情况的表达式都算出来，学生会发现利用追击问题的原理，设运动时间为t秒，则∠BPM=2t，∴∠BPN=180﹣2t，∠DPM=30﹣2t，∠APN=3t.∴∠CPD=180﹣∠DPM﹣∠CPA﹣∠APN=90﹣t，∴==。而∠BPN+∠CPD=180﹣2t+90﹣t=270﹣3t，可以看出∠BPN+∠CPD随着时间在变化，不为定值。

教师在指导学生分组合作时，要适当将基础好的学生与基础稍差的学生搭配编组，这样能更有效地发挥学生之间的相互补差，相互学习的作用。教师再根据学生的情况提出不同层次的问题进行引导。这样能更好地照顾学生间的差异性，推动探究活动的有效进行。

四、运用课堂自主练习，引导学生巩固理解

课堂练习是课堂教学过程中的一个重要环节，是使学生进一步巩固和掌握新知、形成技能获得能力培养、深化学生自主探究的过程。把握好这个环节，可以提高课堂教学效益，帮助学生达到知识迁移的目的。因此教师在安排课堂练习时，要从学生的学情出发，分类设计一些具有拓展性、开放性、探究性的问题、让学生都能参与，积极思考发现问题的不同答案，寻找最佳解题方法。让每个学生都有收获，鼓励学生自己做、自己讲、自己问。

综上所述，新课改的实施要求我们在教学中要改变过去只注重知识传授的倾向，特别强调要以学生为主体，把学习主动权还给学生，凸显学生的主体地位。通过这种方式，有利于调动学生积极性，有利于师生间的情感沟通和信息交流，培养学生自主学习的习惯，形成师生间合作学习、探究学习的良好氛围。