一类具偏差变元二阶微分方程周期解的存在性*

邓瑞娟(芜湖职业技术学院，安徽芜湖241000)

一类具偏差变元二阶微分方程周期解的存在性*

邓瑞娟
(芜湖职业技术学院，安徽芜湖241000)

主要利用Mawhin延拓定理研究一类二阶具偏差变元微分方程x″(t)+f(t，x(t)，x(t－τ0(t))，x'(t))+β(t)g(x(t－τ1(t)))=p(t)的周期解问题，得到了存在周期解的两个充分条件.

Mawhin延拓定理;偏差变元;周期解

1　基础知识

近年来，具偏差变元的微分方程由于其在控制论、生物学等很多领域有重要应用，一直受到人们的广泛关注，也已经有了一定的成果［1-9］.此处主要是运用重合度理论的Mawhin延拓定理研究如下具偏差变元二阶微分方程的周期解:

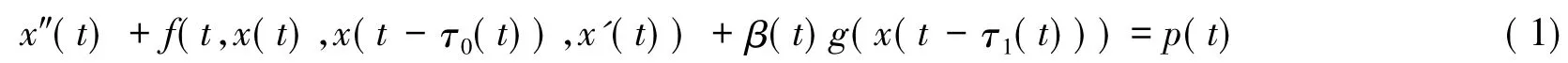
其中，f(t，x，y，v)是R4上的连续函数，同时还是以T为周期的函数.而g(x)，β(t)，p(t)，τ0(t)和τ1(t)均为R上的连续函数，其中β(t)，p(t)，τ0(t)和τ1(t)都是以T为周期的函数.

于是

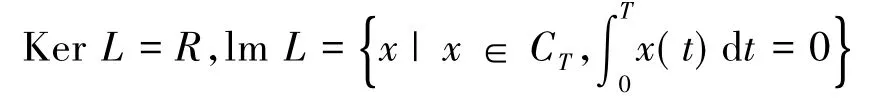
显然，L是指标为零的Fredholm算子.假定P，Q为投影算子

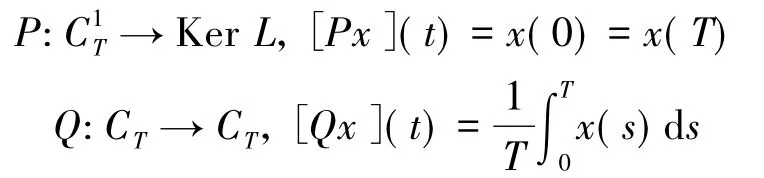
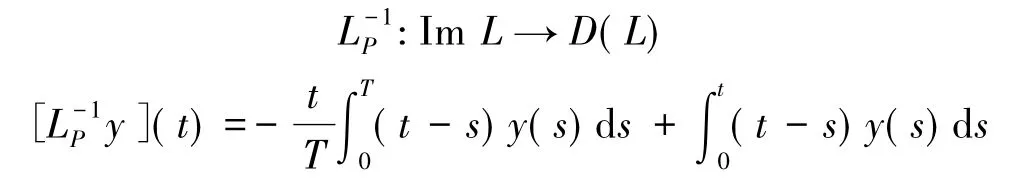
下面给出将会使用到的引理.

引理1［4］(Mawhin延拓定理)设X，Y为Banach空间，L:D(L)⊂X→Y是指标为零的Fredholm算子，Ω⊂X为有界开集上是L－紧的，如果下列条件满足:

则方程Lx=Nx在Ω∩D(L)上至少存在一个解.

2　主要结果

定理1设方程(1)满足条件:

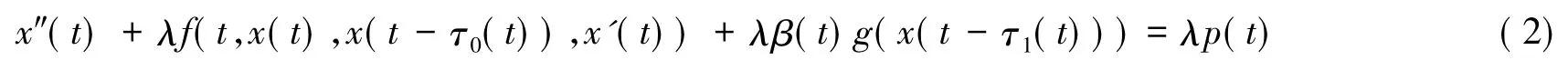
下面证明存在ξ∈R，使得

于是有

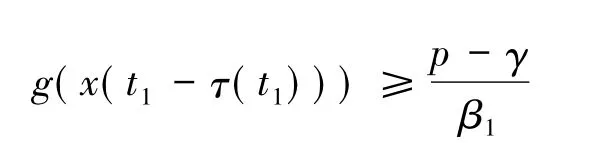
令t2为x(t)在R上取得最小值的点，则x'(t2)=0，x″(t2)≥0，由式(2)得

下面讨论:

(Ⅰ)若t2=t1，则x(t)≡C，且，则存在ξ∈R，使得

(Ⅱ)若t2≠t1，由式(6)知存在常数K2＞0，有x(t2－τ1(t2))＜K2．

(A)若x(t2－τ1(t2))∈(－K1，K2)，则取ξ=t2－τ1(t2)，此时有

(B)若x(t2－τ1(t2))＜－K1，由式(5)及x(t)的连续性及介值定理知一定存在t1－τ1(t1)，t2－τ1(t2)之间的某个ξ，使得

因此

由于x(0)=x(T)，故必有t*0∈［0，T］，使得，同上可得

于是

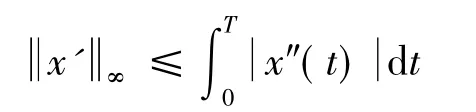
将式(2)两端同乘以x'(t)，并在［0，T］上积分，得

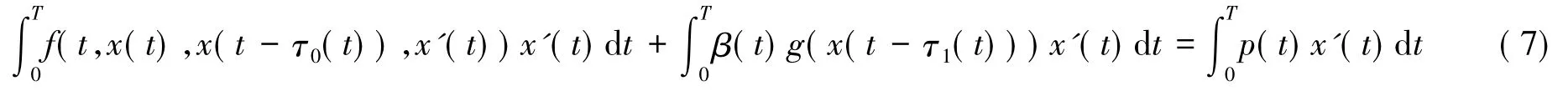
由定理1的条件①可得

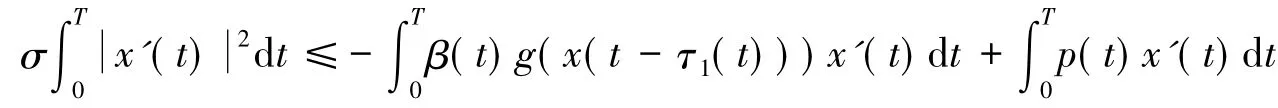
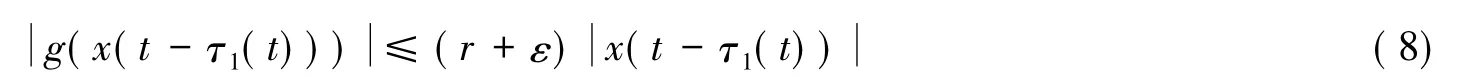
则由式(9)-(11)和柯西不等式可得

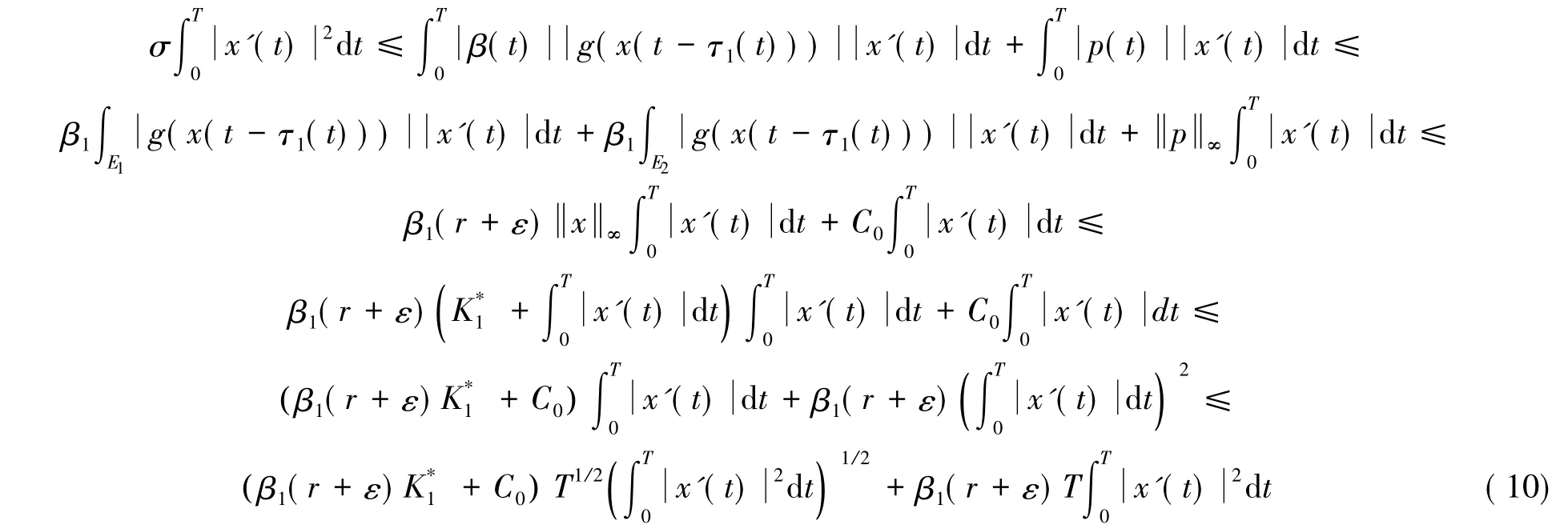
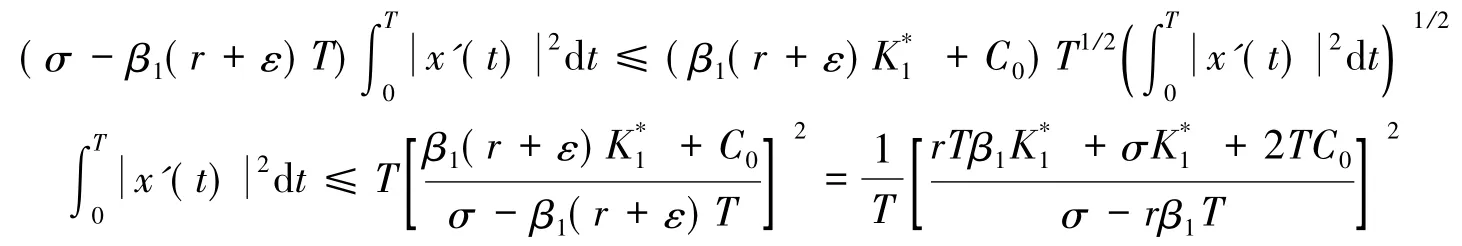
由此可得

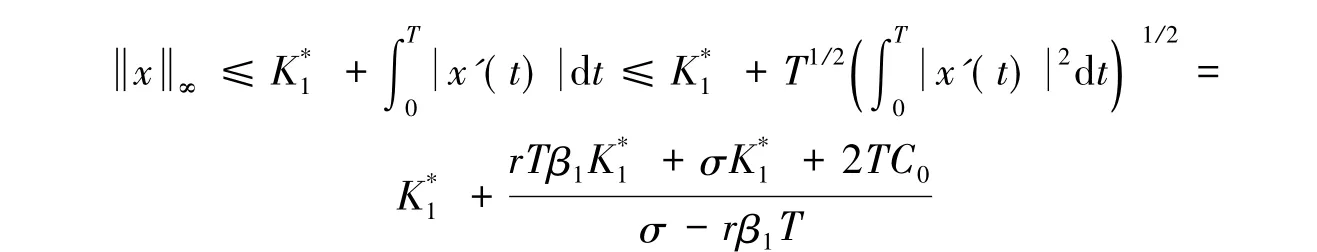
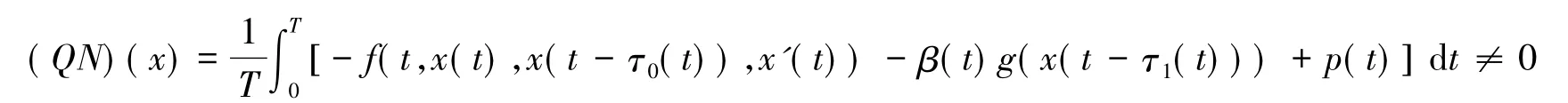
作变换

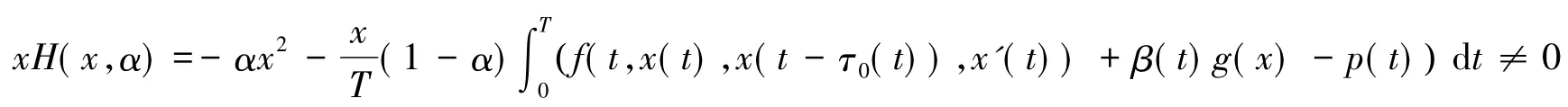
故H(x，α)为同伦映射，取J为恒同映射，有

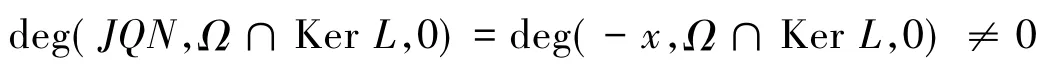
由引理1知，方程(1)至少存在一个T－周期解.

为了下面的证明，假设f(t，x，y，v)=f1(t，x，y，v)+f2(t，x，y，v)，其中f1(t，x，y，v)和f2(t，x，y，v)均在R4上连续，且(t，x，y，v)∈R4，f1(t，x，y，v)和f2(t，x，y，v)都是关于t的T－周期函数.

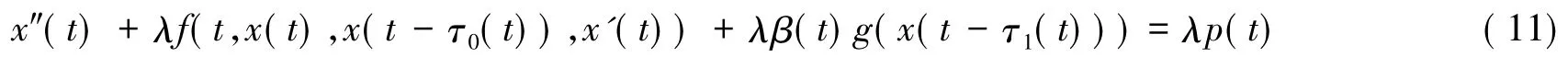
类似于定理1中的证明，可知存在t'0∈［0，T］和，使得，其中是与λ无关的常数.

另有

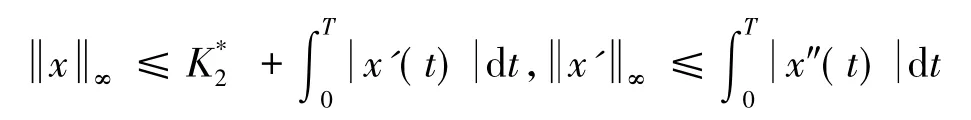
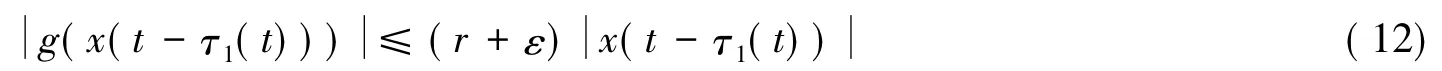
因为x(0)=x(T)，由罗尔定理可知存在t3∈［0，T］，使得x'(t3)=0.在式(11)两边同乘以x'(t)，并从t3到t积分，于是有

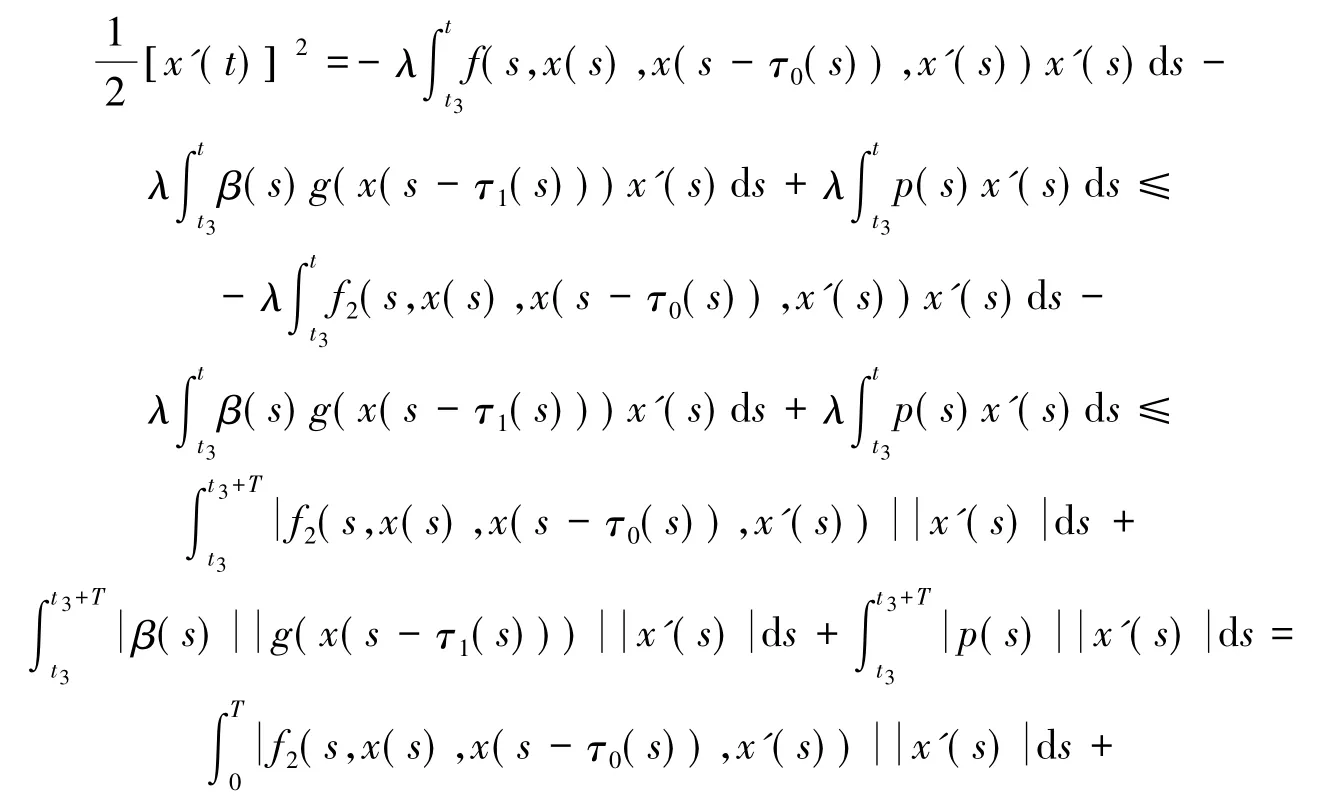
其中C0定义同前，则

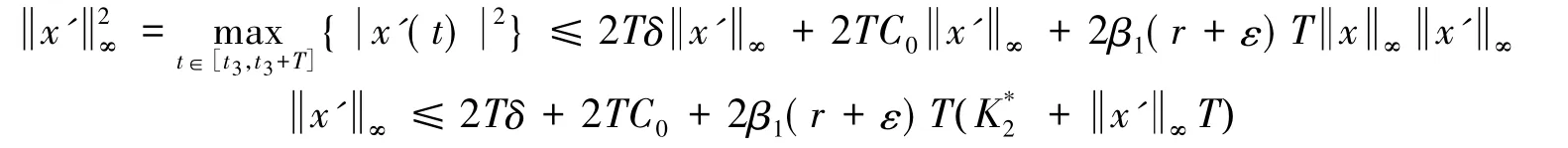
因此

其余证明同定理1，此略.证毕.

［1］DING T R.Nonlinear Oscillations at a Point of Resonance［J］.Science in China(ser A)，1982，25(9):918-931

［2］葛渭高.一类n维!Liénard方程的调和解［J］.数学年刊，1990，11A(3):297-307

［3］黄先开.具有时滞的保守系统的2π周期解［J］.系统科学与数学，1989，9(4):298-308

［4］施吕蓉，周宗福，高伟.一类二阶具多偏差变元微分方程的周期解［J］.山西师范大学学报:自然科学版，2012，26(4):12-17

［5］鲁世平，葛渭高.一类二阶具偏差变元的微分方程周期解［J］.数学学报，2002，45(4):811-818

［6］郭承军，王根强.一类二阶具多偏差变元微分方程周期解的存在性［J］.中山大学学报:自然科学版，2007，46(6):5-9

［7］汪娜，鲁世平.一类三阶具偏差变元微分方程的周期解［J］.安徽师范大学学报:自然科学版，2006，29(1):17-22

［8］施吕蓉，周宗福，高伟.一类三阶具多偏差变元微分方程的周期解［J］.重庆工商大学学报:自然科学版，2013，30(1):6-15

［9］OMARIP，ZANOLIN P.Anote on Nonlinear Oscillation at Resonance［J］.Acta Math Sinica，1987，3(3):351-361

Periodic Solutions of the Second Order Differential Equation with Deviating Arguments

DENG Rui-juan
(Wuhu Institute of Technology，Wuhu 241000，China)

Using the Mawhin continuation theorem，this paper studies a class of periodic solutions of the second order differential equation with deviating arguments x″(t)+f(t，x(t)，x(t－τ0(t))，x'(t))+ β(t)g(x(t－τ1(t)))=p(t)，and two sufficient conditions of the periodic solutions are obtained.

the Mawhin continuation theorem;deviating arguments;periodic solutions

O175.1

A

1672－058X(2015)09－0061－05

10.16055/j.issn.1672－058X.2015.0009.016

2015－01－15;

2015－02－20.

安徽省2013年度省级自然科学研究项目(KJ2013B347);安徽省2013年度省级自然科学研究项目(KJ2013B348).

邓瑞娟(1984-)，女，安徽芜湖人，讲师，硕士，从事微分方程研究.