基于二尖瓣时变电阻模型的左心血液循环系统建模与仿真

温太阳 王芳群 王 颢 贺照明,2*

1(江苏大学电气信息工程学院,江苏 镇江 212013)2(德州理工大学机械工程系，美国，德克萨斯州，拉伯克 79409)

基于二尖瓣时变电阻模型的左心血液循环系统建模与仿真

温太阳1王芳群1王 颢1贺照明1,2*

1(江苏大学电气信息工程学院,江苏 镇江 212013)2(德州理工大学机械工程系，美国，德克萨斯州，拉伯克 79409)

改善传统血液循环系统数值仿真研究中关于二尖瓣流量的模拟仿真，充分考虑二尖瓣反流的客观存在性，并对二尖瓣动力学特性及二尖瓣运动在血液循环中的影响作用进行深入研究。根据血液动力学和电学网络的等效关系，提出基于时变电阻的二尖瓣电路模型，同时考虑血液在左心室的惯性及二尖瓣闭合的滞后性，建立改进型的左心血液循环系统等效电路模型。根据电学分析原理，求得该等效电路的状态微分方程数学模型。应用Matlab对数学模型进行建模仿真，结果得到更加符合生理要求的二尖瓣流量仿真曲线。二尖瓣流量分为3部分：舒张期的正向流量、收缩期关闭反流量和泄漏反流量。并且,二尖瓣流量充满心脏舒张的整个时期。在收缩期，可以明显看到正常反流延迟二尖瓣跨瓣压差，时间为50～80 ms。该研究揭示了二尖瓣在收缩期闭合速度和闭合质量对二尖瓣反流流量的影响。

时变电阻；二尖瓣；左心血液循环；血液动力学

引言

血液循环系统是人和动物生命过程中最重要的系统之一。对血液循环系统的建模方法有很多，其中采用数值仿真可以弥补传统动物实验代价高、周期长等缺点。根据血液动力学与电学系统的等效关系，可将血压等效成电压，血流等效成电流，血流阻力等效成电阻，血流惯性等效成电感，血流顺应性等效成电容，建立血液循环系统的电学网络模型。

对于心脏瓣膜的仿真，传统仿真模型中主要考虑瓣膜对血液的单向流动性作用，均用理想二极管和线性电阻串接来模拟[1-2]。对于瓣膜反流，是当跨瓣压差(瓣膜上游和下游压力差值)为负时，基于瓣膜的反流程度，改变瓣膜数学模型的参数来模拟[3-4]。这些理想化的模型忽略了瓣膜反流的客观存在性，并且未对瓣膜动力学特性及瓣膜运动在血液循环中的影响作用进行深入研究。Leyh在1999年研究发现，瓣膜在一个心动周期内经历快速打开-缓慢关闭-快速关闭3个阶段，并且瓣膜在快速关闭前都有一个回归运动[5]。二尖瓣闭合是一个被动过程，主要是血液流动和跨瓣压差作用的结果。无论健康还是病变的二尖瓣，在左心室收缩期，都存在一定的反流现象[6]。在一个心动周期内，二尖瓣反流量可以分为关闭反流量和泄漏反流量。其中，关闭反流量指二尖瓣在心室收缩初期闭合阶段从左心室流入左心房的血流量，和二尖瓣的闭合速度有关；泄漏反流量是收缩中后期二尖瓣闭合后从左心室漏流到左心房的血流量，反映了二尖瓣的闭合质量。而流经二尖瓣的血流相对于二尖瓣跨瓣压差存在一定的延迟，这种延迟是由二尖瓣闭合运动和血液在左心室的惯性造成的，在心脏收缩期二尖瓣闭合阶段体现得尤为明显[7]。

本研究首先根据血液动力学和电学系统的等效关系，提出基于时变电阻的二尖瓣电路模型，同时考虑瓣膜运动和血液在左心室的惯性，建立改进型的左心血液循环系统模型，并应用Matlab对模型进行仿真。最后，通过和基于二尖瓣传统模型的左心血液循环系统比较，验证仿真结果，得到更加符合生理条件的二尖瓣流量曲线。

1 方法

1.1左心血液循环系统等效电路

根据血液动力学和电学之间的等效关系，建立血液循环系统等效电路，如图1所示。系统由左心房、左心室、二尖瓣、主动脉瓣和动脉系统5部分组成。假设右心部分和肺循环系统完全健康，不影响左心血液循环系统。同时，也不考虑左心房的主动收缩性，因此系统中只用一个电容CR来表征它的被动顺应性[8]。

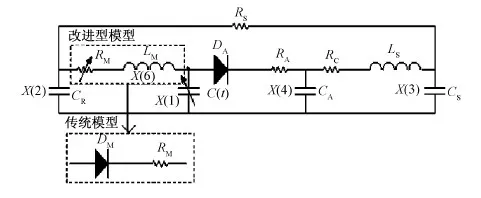
图1 左心血液循环系统等效电路Fig.1 Equivalent circuit of left heart circulatory system

1.2左心室和主动脉系统模型

心室的收缩和舒张功能通常用压力-容积曲线来描述。根据Suga等的研究，左心室的血压与容积关系可用时变弹性函数来表述，其生理意义表征左心室心肌弹性[9]。在本研究中，左心室的仿真建模参考文献[1]，仿真得到左心室的时变弹性函数E(t)波形，如图2所示；动脉系统一般使用集总参数的弹性腔模型，即所谓的Windkessl模型。本文参考文献[3]选用经典的双弹性腔模型(RC，RC，LS，CA和CS)来表述。因左心室模型和主动脉系统模型在参考文献中已有详细描述，所以不再赘述。

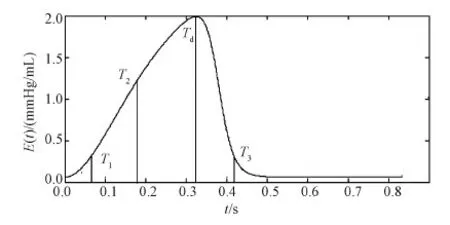
图2 左心室时变弹性函数曲线Fig.2 Curve of the elastance function

1.3瓣膜模型

传统基于线性电阻和理想二极管串接的瓣膜模型，其等效的数学关系为

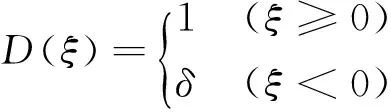
(1)

式中，ξ表示瓣膜跨瓣压差；δ依据瓣膜反流程度在0～1之间取值，δ值越大，表示反流越严重。

假设主动脉瓣完全健康不存在任何病变，所以对于主动脉瓣的仿真仍然理想化为一个二极管和一个线性电阻串联的模型，此时δ=0。

1.3.1二尖瓣传统模型

为了突出改进型二尖瓣模型对左心血液循环系统流体动力学的影响，利用传统的二尖瓣模型来模拟考虑正常反流的健康二尖瓣，此时传统模型的数学表达式(1)中的δ=0.001[3]。

1.3.2二尖瓣改进型模型

本研究提出二尖瓣时变电阻和恒电感串接的模型。其中，时变电阻主要模拟二尖瓣对血液的阻力作用，恒电感主要模拟心室血流的惯性和二尖瓣闭合的滞后性。时变电阻的电阻值根据二尖瓣在一个心动周期内的4个状态下二尖瓣对血液的阻力来确定。这4个状态为：二尖瓣完全张开、二尖瓣闭合过程、二尖瓣完全闭合和二尖瓣开启过程。其中，因为二尖瓣在舒张期的开启过程时间很短，可以看成是阶跃式变化。对于阻力值的计算，依据电学原理，利用二尖瓣跨瓣压差绝对值除以流经二尖瓣的流量即可得到。而二尖瓣的跨瓣压差和二尖瓣流量，则根据文献[6]实验检测所得。电阻阻值数学表达式为

(2)

式中，tc为一个心动周期时间，T1是二尖瓣开始闭合时间点，T2是二尖瓣完全闭合时间点，T3是二尖瓣张开时间点。它们满足如下关系：

(3)

式中，Td为心室弹性函数E(t)达到最大值Emax时的时间点，它们在心室肌弹性曲线上对应的时间如图2所示。

二尖瓣时变电阻如图3所示，其中，RM1值为0.004，表征舒张期二尖瓣完全张开对血液的阻力；RM2表征二尖瓣在收缩初期闭合阶段的阻值变化，文献[6]实验发现二尖瓣闭合阶段的阻值呈幂指数上升；RM3为一恒值15，表征二尖瓣完全闭合时对血液的阻力。

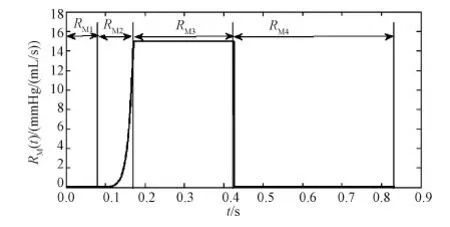
图3 RM值曲线Fig.3 Curves of RM value

1.4状态方程

选取状态变量如表1所示。

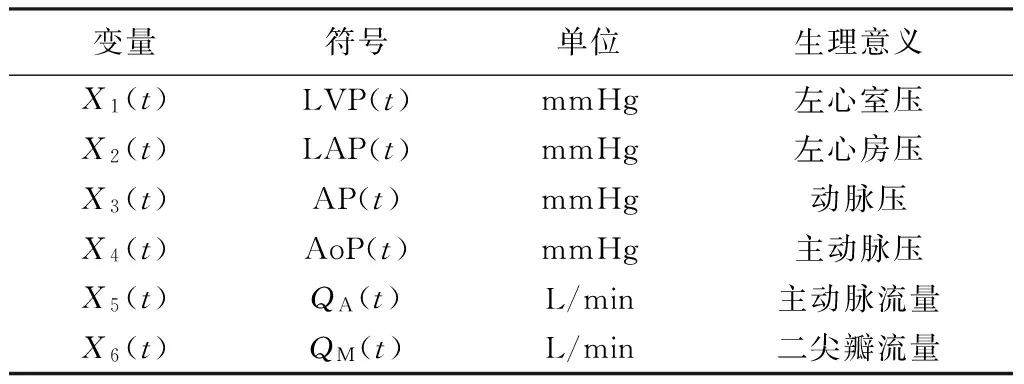
表1 模型状态变量Tab.1 State variables of the system

根据基尔霍夫定律，列出图1所示等效电路图的状态方程为

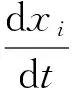
(4)

其中，

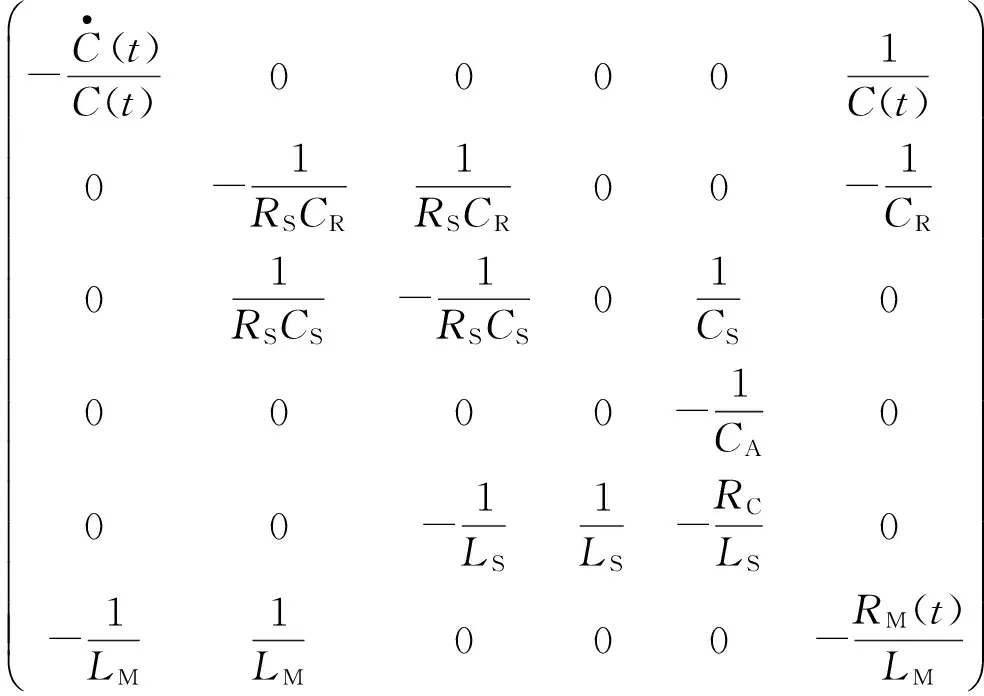
式中，C(t)=1/E(t)，E(t)为左心室的时变弹性函数。

1.5模型仿真

利用Matlab求解状态方程式(4)，得到相应的流体动力学特性曲线。图1的系统参数如表2所示，初始值设置如下：LVP=8.2 mmHg，LAP=7.6 mmHg，AP=67 mmHg，AoP=80 mmHg，QA=52 mL/s，QM=50 mL/s[10]。

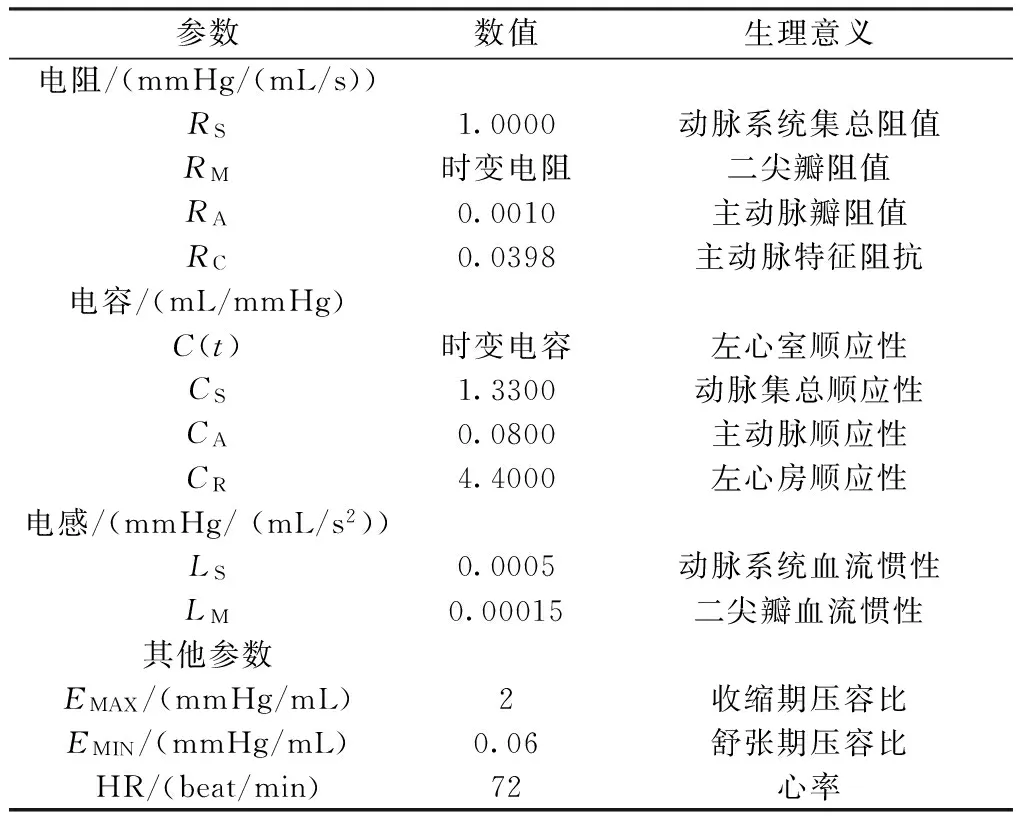
表2 模型参数Tab.2 Model parameters

2 结果

2.1模型验证

根据模型参数设置值，模拟仿真健康人的生理状况，仿真结果如图4、5所示。分别取相邻两个周期内的仿真结果数据，在相同对应时间点上对其进行比较，如果两周期仿真结果数值在对应时间点上的相对误差小于0.1%，则认为系统趋于稳定。从仿真结果可以看出，基于时变电阻二尖瓣模型的左心血液循环系统的各状态参数仿真曲线在第5个周期已经趋于稳定。

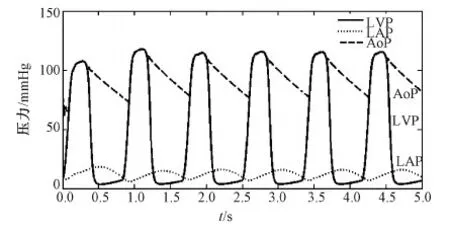
图4 压力曲线Fig.4 Curves of pressure

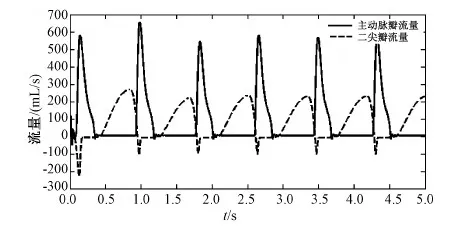
图5 流量曲线Fig.5 Curves of flow

2.2动力学研究

根据式(2)和式(4)及参数设置，得到二尖瓣不同模型下血液循环系统动力学特性，选取稳定后的仿真结果(本研究选取第5～6两个周期)来分析二尖瓣不同仿真模型下的血液循环系统动力学特性，结果如图6～8所示。

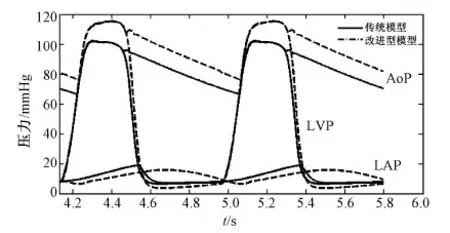
图6 基于二尖瓣两种模型的循环系统压力曲线比较Fig.6 Comparison of pressure simulation curves between the two mitral models

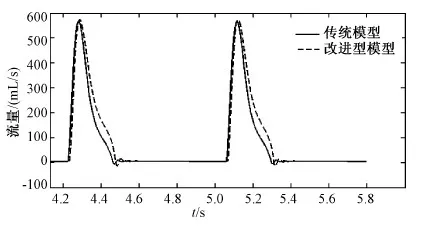
图7 基于二尖瓣两种模型的循环系统主动脉流量比较Fig.7 Comparison of aortic flow simulation curves between the two mitral models

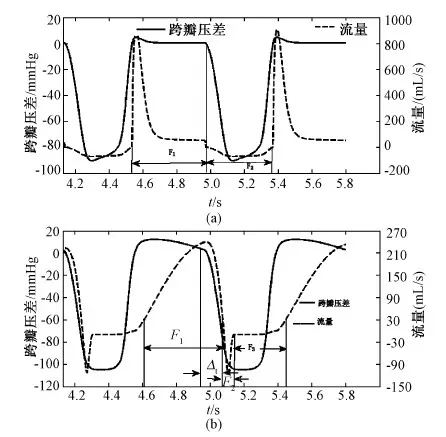
图8 基于两种二尖瓣模型二尖瓣流量与跨瓣压差关系。(a)传统模型；(b)改进型模型Fig.8 Relationship between the mitral flow and transmitral pressure of the two mitral models.(a)Traditional model；(b)Modified model

在正常生理情况下，左心室压力是90～140 mmHg，舒张压0～10 mmHg，压力曲线呈高原型曲线；正常主动脉收缩压90～140 mmHg，舒张压60～90 mmHg；左心房压力在整个周期内压力范围为6～20 mmHg；人体正常心输出量为4.5～6 L/min[11]。表3显示，基于两种仿真模型的左心血液循环系统仿真所得参数值和正常生理值相符。

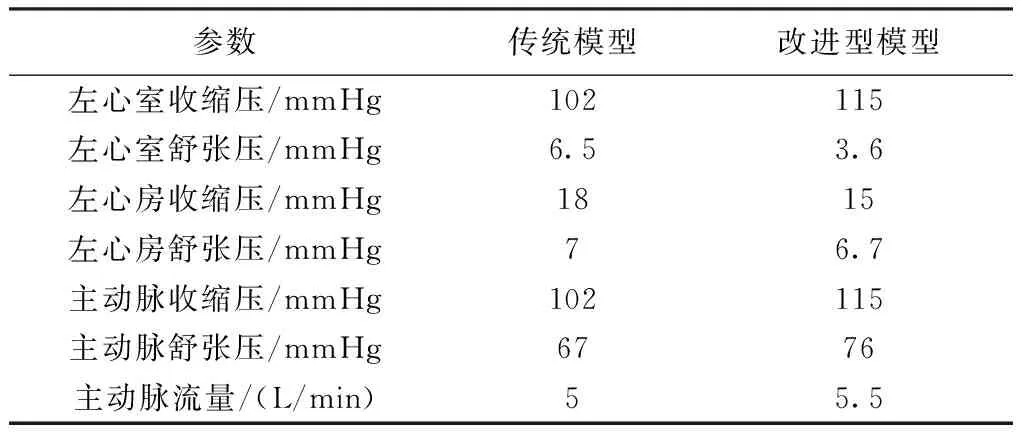
表3 特征参数仿真结果Tab.3 The simulation results of characteristic parameters

图6的压力曲线显示，在心脏收缩期，基于改进型二尖瓣模型仿真得到的左心血液循环系统的左心室压力、主动脉压力高于传统模型的左心室压力、主动脉压力，改进型模型的左心房压力低于传统模型的左心房压力；而在舒张期，改进型模型下的主动脉压力高于传统模型得到的主动脉压力，改进型模型仿真得到的左心房压力随着心室血液充盈缓慢降低。图7表明，基于改进型模型仿真得到的主动脉流量高于传统模型情况下的主动脉流量。

图8中的(a)、(b)两图分别比较了传统模型和改进型模型的二尖瓣流量和跨瓣压差之间的关系。首先，改进型模型的二尖瓣流量可明显地分成3部分：舒张期二尖瓣的正向流量F1、收缩期因二尖瓣闭合过程造成的闭合反流量F2和二尖瓣完全闭合后的正常泄漏量F3。一个心动周期内它们的体积分别是：F1=68 mL，F2=2.1 mL，F3=3.4 mL。其中，闭合反流F1的反流分数为3%，泄漏反流F2的反流分数为5%。而传统模型的二尖瓣流量只分为舒张期的正向流量F1和收缩期的正常反流量F2。一个心动周期内正向流量F1的体积为64 mL，反流量F2的体积为6 mL，反流分数为8%。其次，相比传统模型，改进型模型的二尖瓣流量充满心脏舒张的整个时期。在收缩期，可以明显看到正常反流延迟二尖瓣跨瓣压差一段时间Δt，为50～80 ms，而传统模型中流量和跨瓣压差之间不存在延迟，即Δt=0。

3 讨论

本研究提出了一个二尖瓣仿真改进型模型，并在左心血液循环仿真系统中，通过和传统模型仿真所得血液动力学参数相比较，发现传统模型虽然考虑二尖瓣的正常反流，但仿真结果并未将二尖瓣的反流区分为闭合反流和泄漏反流两部分，并稍微高估了二尖瓣的正常反流，使在收缩期过多的血液从左心室漏流到左心房，从而使仿真得到的左心室压力、主动脉压力和主动脉流量低于改进型模型的相关参数。另外，传统模型仿真的左心房压力却高于改进型模型的仿真结果。

改进型模型不仅将二尖瓣的正常反流明显地区分为两部分，而且同时考虑了心室血液的惯性，从而在心脏收缩期二尖瓣血流延迟于二尖瓣跨瓣压差，使仿真结果更符合文献[6]的实验测量结果。

二尖瓣的关闭反流量和二尖瓣的闭合速度有关，而二尖瓣的泄漏反流量和二尖瓣的闭合质量有关。临床发现，二尖瓣的闭合速度与二尖瓣的瓣环大小有关，而二尖瓣闭合质量反映了二尖瓣的健康状况，和二尖瓣反流程度密切相关。笔者应用时变电阻的二尖瓣模型，将二尖瓣的正常反流量明显地细分成两部分——关闭反流量和泄漏反流量，从而得到更加符合生理条件的二尖瓣流量曲线。这对后续不同瓣环大小和因腱索断裂造成二尖瓣闭合不全等因素下的血液循环系统动力学特性研究具有明显的优势。

然而，笔者主要提出了二尖瓣的时变电阻模型，未考虑主动脉瓣的正常反流，对主动脉瓣的模拟仍然基于血液单向流动性，将其等效为一个电阻和理想二极管的模型，这对整个血液循环系统仿真的准确性将有一定影响；同时，也未对二尖瓣不同反流程度下的血液循环系统进行深入的仿真分析，这都需要后续继续研究。

4 结论

笔者在现有仿真模型的基础上，提出二尖瓣仿真的时变电阻模型，同时考虑心脏收缩期血液在左心室的惯性和二尖瓣闭合的滞后性，引入一个电感，从而更加准确地仿真了血液循环系统中流过二尖瓣的流量，即仿真细致地将二尖瓣在心脏收缩期中的正常反流分为闭合反流和泄漏反流，在心脏收缩期二尖瓣流量延迟二尖瓣两端跨瓣压差。本研究将对二尖瓣反流的细致研究和分析起到辅助作用。

[1] 刘苓苓，李岚，钱坤喜. 改进型五阶集总参数心血管循环系统的建模与仿真 [J]. 中国生物医学工程学报, 2012,31(1):13-19.

[2] 钱坤喜，刘苓苓，李岚，等.体循环系统建模与仿真 [J]. 江苏大学学报, 2012,33(3):278-282.

[3] 冯敏,黄晓阳,苏茂龙.基于双弹性腔的左心血液循环系统的建模与仿真 [J].厦门大学学报, 2012,51(4):676-681.

[4] 冯敏. 二尖瓣关闭不全电路仿真与建模研究 [D]. 厦门: 厦门大学, 2013.

[5] Theodosios K, Shi Yubing. A concentrated parameter model for the human cardiovascular system including heart valve dynamics and atrioventricularinteraction [J]. Medical Engineering & Physics, 2006,28(7): 613-629.

[6] He Zhaommig, Zhang Kailiang, Gao Bo. A novel coaptation plate device for functional mitral regurgitation: an in-vitro study [J]. Annals of Biomedical Engineering, 2014,24(2):2039-2047.

[7] He Zhaoming, Gao Bo, Bhattacharya S,etal. In vitro stretches of the mitral valve anteriorleaflet under edge-to-edge repair condition [J]. Biomech.Eng, 2009,16(4):111-121.

[8] Marwan A, Simaan G, Wang Yu,etal. Left ventricular assist devices:engineering design considerations [J]. New Aspects of Ventricular Assist Devices, 2011,29(8):134-157.

[9] Suga H, Sagawa K,Shoukas. Load independence of the instantaneous pressure -volume ratio of the canine left ventricle and effects of epinephrine and heart rate on Circulation research, 1973,32(3):314-322.

[10] Marwan A, Simaan L, Antonio F,etal. A dynamical state space representation and performance analysis of a feedback-controlled rotary left ventricular assist device [J]. IEEE Trans Biomed Eng, 2009,17(1):15-28.

[11] 岳利民. 生理学 [M]. 北京: 科学出版社, 2002: 35-44.

Modeling and Simulation of Left Ventricular Circulation System Based on the Mitral Valve Model of Time-Varying Resistance

Wen Taiyang1Wang Fangqun1Wang Hao1He Zhaoming1,2*

1(School of Electrical and Information Engineering, Jiangsu University， Zhenjiang 212013, Jiangsu, China)2(Department of Mechanical Engineering,Texas Tech University，Lubbock，TX 79409，USA)

time varying resistance；left ventricular circulation system；mitral model；hemodynamic

10.3969/j.issn.0258-8021. 2015. 03.016

2014-11-10， 录用日期:录用日期：2014-12-25

江苏省高层次创新创业人才引进计划基金; 江苏省江苏特聘教授计划基金

R318

D

0258-8021(2015) 03-0370-06

*通信作者(Corresponding author)， E-mail: hezhaoming@ujs.edu.cn