基于TOPSIS法的多属性危险化学品运输路径优化

佘洋洋，鲁顺清，王艳丽，张义英

(中国地质大学(武汉)工程学院，湖北 武汉 430074)

基于TOPSIS法的多属性危险化学品运输路径优化

佘洋洋，鲁顺清，王艳丽，张义英

(中国地质大学(武汉)工程学院，湖北 武汉 430074)

危险化学品道路运输事故时有发生，由此造成的损失十分巨大，选择合适的运输路径可有效降低运输风险。利用有向网络图来表示交通运输网络，考虑运输路径的多属性，用事故率、运费、应急救援能力和暴露人数4个因素来描述路段属性，建立了多属性危险化学品运输路径优化模型，并通过设计遗传算法来求解该模型，进行路径优化选择。求解过程中采用TOPSIS法来计算路径的综合属性，同时将计算得到的综合属性值作为遗传算法运行过程中对应个体的适应值，并通过设计的遗传算法使算法在运行过程中选择压力由小变大，从而选择出最优路径。实例运行结果表明：当改变某路段的属性值时，会重新搜寻到最优路径，因此基于TOPSIS法建立的危险化学品运输路径优化模型具有较好的求优能力。

危险化学品；道路运输；路径优化；TOPSIS法；有向网络图

危险化学品运输车辆在运输过程中发生事故，将对事故发生路段周边的人、车辆、建筑物、环境等构成很大的风险[1-3]，若选择合理的危险化学品运输路径，将可有效地降低运输风险。但在实际运输过程中，路段具备多个属性值，这便给路径选择带来较大的困难。

目前关于危险化学品运输路径的相关研究较多，如邵辉等[5]采用GA法来进行路径优化，但对于路段的属性只用运输路段的风险来代替；杨信丰等[6]用5个要素来描述路段属性，分别为路段行驶时间、路段事故率、交通损失、暴露人数、应急响应能力，具有一定的实用性，而对于路径多属性的处理则利用信息熵法来确定路段综合属性值；宋洋等[7]用蚂蚁算法对危险化学品运输路线进行优化，并利用经济成本和风险成本进行加权求和的结果作为路径优化目标；吴缝等[8]、高清平[9]针对路段属性具有不确定性，采用模糊方法来进行处理；刘萌斐等[10]建立起一种新的计算危险品道路运输事故概率的方法。

基于上述研究，本文针对危险化学品运输道路多属性较难处理的问题，利用TOPSIS法来计算路径的综合属性值，通过综合属性值大小来比较各路径的优劣，在此基础上建立多属性危险化学品运输路径优化模型，并通过设计遗传算法来进行路径优化选择。

1 多属性危险化学品运输路径优化模型的建立

1.1 指标的选取

考虑运输路径多属性，本文在路段评价指标体系选择上，通过查阅相关文献[6,11-13]，结合危险化学品运输过程中运输成本、发生运输事故的诱因、事故发生后果的严重程度以及事故发生后的可挽救能力，并考虑到指标体系的可操作性原则，选用路段属性指标事故率、运费、暴露人数和应急救援能力4个因素作为评价指标。

1.1.1 事故率

路段事故率用以表征选定路段在一年内平均每一万辆机动车中发生的事故次数，其表达式为

(1)

式中：P为对象路段的事故率[次/(年·万辆)]；X为对象路段在一年内发生的事故次数(次)；Y为对象路段在一年内通过的车辆数(辆)。

1.1.2 运费

路段运费是指危险化学品运输车辆通过对象路段所需费用，包括油费、车辆保养费、维修费以及交付给运输人员的费用等。

1.1.3 暴露人数

路段暴露人数包括对象路段所在区域中路上人数及周边建筑物内的人数。周边建筑物内的人数指一旦危险化学品运输车辆在对象路段上发生泄漏等事故时，受到威胁的建筑物内的人数。

1.1.4 应急救援能力

路段应急救援能力主要体现在对暴露人口的疏散、事故现场伤员的处理以及事故后现场处理等方面的快速反应能力，实施这些救援的部门包括医疗、消防等机构。本文选取对象路段与最近的应急救援部门间的距离来表示对象路段的应急救援能力。

1.2 模型的建立

图1为4节点有向网络图，其中v1、v2、v3、v4分别代表4个路口;ev1v3为v1、v3两路口连接成的路段，R13={rev1v31，rev1v32，rev1v33，rev1v34}为路段1→3的4个属性值的集合;C1→3→4=R13+R34为路径1→3→4的4个属性值的集合。

1.3 路径多属性处理方法

TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)法由Hwang和Yoon于1981年首次提出，是一种多属性决策方法[14-15]。该方法要求每个属性变化趋势一致，因此本文选取的路段属性指标事故率、运费、暴露人数和应急救援能力均越小越好，这样才能符合要求。此外，在进行TOPSIS法处理前，必须对路段的各个属性值进行归一化处理，具体处理方法和步骤如下：

设共有n条路径，归一化后的属性值矩阵为

c11c12c13c14

c21c22c23c24

⋮⋮⋮⋮

cn1cn2cn3cn4

第一步：找到各属性最大值组成的个体cmax=(cmax1，cmax2，cmax3，cmax4)以及各属性最小值组成的个体cmin=(cmin1，cmin2，cmin3，cmin4)，其中cmaxi、cmini分别为当前所有路径中第i个属性的最大值和最小值。

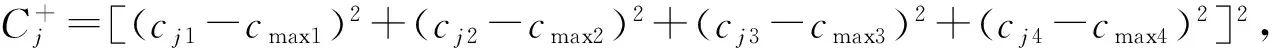
2 设计遗传算法求解模型

在遗传算法求解问题过程中，可通过自行设计适应值函数、选择策略、交叉策略、变异策略等来改变算法的搜索方向和效率。本文通过改进遗传算法的选择策略，使种群在进化过程中的选择压力由小变大。

2.1 编码方式

模型中用有向网络图来表示交通网络，由于选取的路径可能长短不一，因此路径所通过的结点数也是随之变化的。基于此，本文采用文献[16]中提出的优先级染色体编码方式，该编码方式虽然是定长的，但通过优先级编码后得到的解码路径长度是可变的。对图2有向网络图的优先级编码方式及其解码路径见图3。由图2和图3可见，与节点1连接的分别为结点2和结点3，比较两节点的编码大小，节点2小于节点3，所以选择节点3作为解码路径的下一节点，依次类推，直至节点9。

2.2 遗传算子设计

2.2.1 选择算子

选择算子的作用是从父代和子代混合种群中挑选出固定数量的个体作为下一个父代种群，而选择策略的不同会导致不同的选择压力[17-18]。在遗传算法运行初期，为保证算法具有较好的全局搜索能力，初期的选择压力应较低；而在其运行后期求解最优解时，要保证此时算法具有较好的求精能力。本文根据文献[9]对适应值的处理，通过计算每个个体被选的期望数，依据期望数大小来选取个体，具体选择策略如下：

2.2.2 交叉算子

本文采用文献[8]中提出的优先级索引交叉算子，该交叉算子具有较好的继承性和优越性，具体操作步骤如下(以图1为例)：

第一步：随机选择交叉点，得到交叉点右侧互换染色体片段S1、S2，并对S1、S2进行互换，见图4和图5。

第二步：对染色体片段S1、S2进行排序，建立索引映射关系，见图6。

第三步：依据索引关系，得到交叉后的子代个体，见图7。

2.2.3 变异算子

变异算子的具体操作步骤为：随机产生两个不大于染色体长度的自然数，自然数对应染色体相应位置上的基因，互换两个自然数对应位置上的基因，得到变异后的染色体。若产生的两个自然数相同，则不进行交换操作。

3 实例分析

本文利用图8有向网络图来对建立的多属性危险化学品运输路径优化模型和设计的遗传算法进行检验。为测试算法的准确性，分别设定1→2路段的应急救援能力为0.5km和3km，遗传算法运行结果见表1。求解算法均在MATLAB7.8下编程实现，并设置遗传算法种群规模为50，交叉率为0.7，变异率为0.2，进化代数为50。

由表1可见：当1→2路段的应急救援能力设为0.5km时，算法运行后得到的最优路径为1→2→5→9→13→16→19→20，次优路径为1→3→7→11→15→18→20；当1→2路段的应急救援能力设为3km时，即降低了包含1→2路段的路径的应急救援能力，算法运行后得到的最优路径为1→3→7→11→15→18→20，次优路径为1→2→5→9→13→16→19→20。

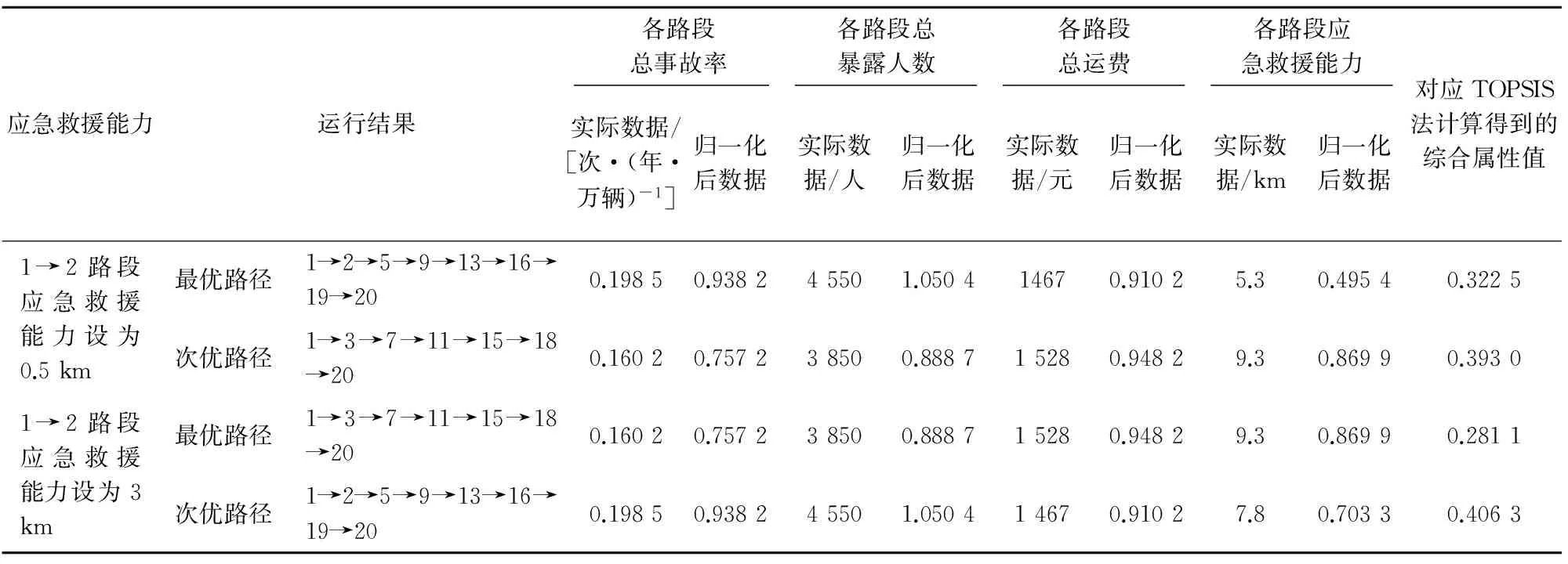
表1 遗传算法运行结果

4 结 论

针对建立的多属性危险化学品运输路径优化模型，当降低1→2路段的应急救援能力时，遗传算法运行后得到的最优路径和次优路径均发生了改变，求得的路径均为当前的最优路径和次优路径。因此，利用TOPSIS法来处理危险化学品运输路段多属性问题，具有较好的效果。

[1] 李建，白晓昀，任正中，等.2011—2013年我国危险化学品事故统计分析及对策研究[J].中国安全生产科学技术，2014，10(6)：142-147.

[2] 辛春林，王金连.危险化学品运输事故历史数据研究综述[J].中国安全科学学报，2012，22(7)：89-93.

[3] 张宏，李杰，吕宜生.突发公共事件应急交通研究综述[J].安全与环境工程,2014，21(5)：164-168.

[4] 麻存瑞，马昌喜.不确定环境中危险品运输路径鲁棒优化[J].中国安全科学学报,2014，24(3)：91-95.

[5] 邵辉，李晶，杨丽丹.基于多目标优化的危险化学品运输模式探讨[J].中国安全生产科学技术,2010，6(2)：51-55.

[6] 杨信丰，李引珍，何瑞春，等.多属性时间依赖网络的城市危险品运输路径优化[J].中国安全科学学报,2012，22(9)：84-88.

[7] 宋洋，徐桢，王燕青.基于蚂蚁算法的危险品运输路径优化研究[J].安全与环境工程，2014，21(1)：148-152.

[8] 吴锋，王晓艳.基于模糊Petri网的危险品运输安全评估模型及应用[J].中国安全科学学报，2011，21(1)：95-98.

[9] 高清平.基于可能-概率测度转换的危险品运输风险分析[J].中国安全科学学报，2011，21(3)：90-93.

[10]刘萌斐，钱瑜，夏秋.基于层次分析和模糊综合评价的区域危险品道路运输事故概率评估[J].安全与环境工程，2014，21(6)：171-176.

[11]殷国强.危险品运输网络优化与路段分类管理研究[D].哈尔滨：哈尔滨工业大学，2011.

[12]王云鹏，孙文财，李世武，等.基于ArcGIS的危险品城市运输路径优化模型[J].吉林大学学报(工学版)，2009，39(1)：45-49.

[13]任常兴，吴宗之.危险品道路运输选线问题分析[J].安全与环境学报，2006，6(2)：84-88.

[14]陈西蕊，张蓉珍.TOPSIS法在区域生态安全动态评价中的应用[J].西北农林科技大学学报，2011，39(7)：177-183.

[15]陈强，杨晓华.基于熵权的TOPSIS法及其在水环境质量综合评价中的应用[J].环境工程，2007，25(4)：75-77.

[16]阎啸天，武穆清.基于GA的网络最短路径多目标优化算法研究[J].控制与决策，2009，24(7)：1104-1109.

[17]冯冬青，王非，马雁.遗传算法中选择交叉策略的改进[J].计算机工程，2008，34(19)：189-191.

[18]刘世清，杨孔雨.求解TSP问题的遗传算法改进研究[J].北京信息科技大学学报，2014，29(2)：46-50.

Route Optimization of Hazardous Chemicals Transportation with Multi-attributes Based on TOPSIS Method

SHE Yangyang，LU Shunqing，WANG Yanli，ZHANG Yiying

(FacultyofEngineering,ChinaUniversityofGeosciences,Wuhan430074,China)

Road transportation takes up a large portion in the transportation industry of hazardous chemicals.However,accidents of hazardous chemicals transportation happen every year,which leads to huge loss.Selection of an appropriate route will reduce the risk of hazardous chemicals transportation.Considering the multi-attributes,this paper uses the directed network graph to stand for the transportation network and applies such four factors to describing the attributes of each road as accident rate,cost,emergency response capacity and exposure population.Then the paper establishes a physical model for route optimization of hazardous chemicals transportation with multi-attributes and designs the Genetic Algorithm to solve the model.The study applies TOPSIS method to computing the synthesized attributes.At the same time,the paper regards the synthesized attribute value as the adaptive value during the process of Genetic algorithm and changes the selection pressure from low value to high value in the design of genetic algorithm to search the optimal path.The results show that the designed genetic algorithm can quickly find the optimal path,and when attributes of a road change,the algorithm will search new optimal path again,which shows that the model has a good optimization ability.Key words:hazardous chemical； road transportation； path optimization；TOPSIS method；directed network graph

1671-1556(2015)04-0114-05

2014-12-22

2015-05-22

佘洋洋(1990—)，男，硕士研究生，主要研究方向为危险化学品运输管理。E-mail：1433637501@qq.com

X913；U491

A

10.13578/j.cnki.issn.1671-1556.2015.04.020

鲁顺清(1963—)，男，副教授，主要从事安全管理、安全评价等方面的研究。E-mail：wuhanlsq@sohu.com