地下水位变化对地震地面运动的影响*

李伟华 赵成刚

（中国北京 100044 北京交通大学土木建筑工程学院）

引言

场地地震反应问题，即局部场地条件对地震波传播的影响问题，作为地震工程学中的两大类波动问题之一，一直备受关注．在过去的几十年里，国内外对局部场地条件动力反应问题进行了大量的研究，目前对地形、地貌、覆盖层的组成、厚度、土的软硬等局部场地条件对地震地面运动的影响都进行了相关研究（Trifunac，1972；刘晶波，1989；李伟华，2004）．但综观已有场地地震反应问题的研究中，均未考虑地下水位变化对地震地面运动的影响．而在实际地层中，地下水位是存在的，并且降水、季节变化以及地下水抽取等还将导致地下水位的变化．以北京地区为例，1999年平原地区地下水埋深为15m左右．1999年以后，因连续遭遇枯水年，全市地下水位埋深直线下降，1999—2009年10年间全市累计降深达9．86m（杨忠山等，2010）．地下水位变化是否会对地震地面运动产生影响？将会产生怎样的影响？目前还没有文献分析此问题．究其原因，主要是由于现有场地反应问题研究中，大多以经典弹性动力学为理论依据，将天然土体简化为理想的各向同性单相介质进行分析，这一简化自然忽略了地下水的影响．众所周知，自然界中的土一般是由土骨架和孔隙流体（水和气体）组成的三相介质．当孔隙中完全被水填充时称为水饱和土；当孔隙中仅被气体充满时为干土，或称为气饱和土．土孔隙中流体的性质不同，会导致土层振动时刚度的变化，从而影响土层的动力反应，所以采用常规的单相介质模型来模拟饱和土层显然不合适，应该利用流体饱和多孔介质理论来研究饱和土层．周新民等（2006）曾研究地震波在水饱和与气饱和土层界面上的反射和透射问题，结果表明地震波在水饱和土中的传播与在气饱和土中的传播差异较大．据此可以初步推断，地下水变化应该会对地震地面运动产生影响，但具体影响程度及相关因素还有待进一步研究．

本文以Biot（1956）提出的流体饱和多孔介质波动理论为基础，建立了成层地基模型，把地下水位以下的饱和土层用水饱和多孔介质模拟，地下水位以上土层用气饱和多孔介质模拟．通过研究入射平面简谐波在成层地基中的传播，分析了地下水位变化对地震地面运动的影响．

1 分析模型

本文所用的分析模型如图1所示．该模型为一基岩层上覆有限厚度的覆盖层，覆盖层厚度为H，地下水埋深于地表下h1处．设地下水位上下土层为饱和度不同的同一种土．地下水位以下为水饱和土层（水饱和度Sr＝100%），厚度为h2＝H－h1；地下水位以上土层为干土层（即气饱和土层，水饱和度Sr＝0），厚度为h1．在地表面、地下水位面及基岩表面处的坐标系分别如图1所示．

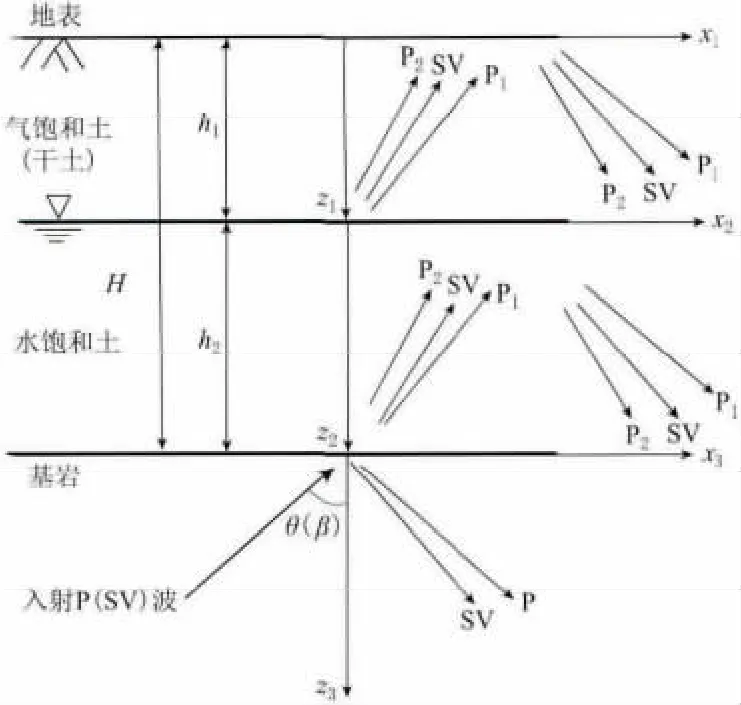
图1 分析模型Fig．1 Analysis model

上覆土层（水饱和或气饱和土层）用流体饱和多孔介质模拟，考虑固体颗粒及孔隙的流体压缩性以及流固两相的惯性耦合和黏性耦合，Biot（1956）给出了流体饱和多孔介质的矢量波动方程：

式中：us和uf分别为固体骨架和流体的位移矢量；e＝▽·us，ε＝▽·uf；ρ11＝（1－n）ρs＋ρ，ρ12＝－ρ，ρ22＝nρf＋ρ，ρs为固相的质量密度，ρf为流体的质量密度，ρ为流固两相耦合的质量密度，n为流体饱和多孔介质的孔隙率；b为与渗流有关的系数，b＝n2η／k（η为流体黏滞系数，k为渗透系数）；A，N，R，Q为材料常数，其中A和N类似于一般弹性理论中的拉梅常数，R和Q反映了流体的弹性及流体与固体骨架间的弹性相互作用，它们可以分别用土骨架和孔隙流体的材料常数来表示（Biot，Willis，1957）：

式中，K＝K［1＋n（－1）］，K和K分别为土颗粒和土骨架的体积模量，λ和μ为土

dssb骨架的拉梅常数，Kf为孔隙流体的体积模量．

因为地下水位上下土层为同一种土，所以地下水位上下土体骨架的拉梅常数相等．土颗粒密度相等．地下水位以下水饱和土的孔隙流体体积模量Kf＝Kw（Kw为水的体积模量），孔隙流体密度ρf＝ρw（ρw为水的密度）；地下水位以上气饱和土的孔隙流体体积模量Kf＝Ka（Ka为空气的体积模量），孔隙流体密度ρf＝ρa（ρa为空气的密度）．本文假定地下水位变化不引起土体孔隙率的变化．

在Biot模型中，土颗粒和孔隙流体均为可压缩的，固体骨架部分与流体部分的应力－应变关系分别为

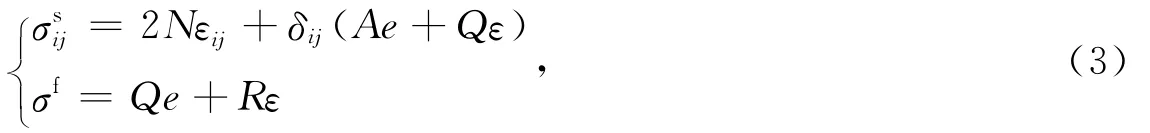
式中，σsij和σf分别为固体骨架部分和流体部分承担的应力，εij＝（ui，j＋uj，i）／2为土骨架应变．基岩用单相弹性介质模拟，其波动方程为（Eringen，Suhubi，1975）

式中：θ＝divub，ub为基岩介质的位移向量；λb和μb为基岩层的拉梅常数；ρb为基岩层的质量密度．

2 波场分析

根据Helmholtz定理，式（1）和式（4）中的位移矢量可写成如下形式：

式中，φ为标量势函数，φ为矢量势函数．将式（5）分别代入式（1）和式（4）中，并假设平面波解形式为简谐波，可分别得到流体饱和多孔介质和单相弹性介质中各形态波的标量势函数φ和矢量势函数φ 的表达式，详见文献（Deresiewicz，Rice，1962；Eringen，Suhubi，1975）．

设P（或SV）波从基岩入射到上覆土层，入射P（或SV）波频率为ω，入射角为θ（或β），则入射波场的势函数可表示为

式中，Aib（或Bib）为入射波幅值，kbP和kbS分别为入射P波和入射SV波的波数．

入射波将在地层内产生反射和透射，各土层中的波场如图1所示，具体分析如下：

1）基岩中．波从基岩层入射到上覆土层中时，在基岩层中产生的反射波为

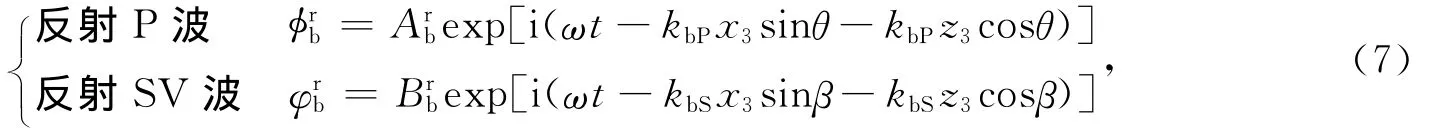
式中，Arb和Brb为待求的基岩中反射波波幅系数．

2）地下水位以下土层（水饱和土层）中．研究表明，流体饱和多孔介质中存在3种类型波：P1波、P2波和SV波．对于此问题，地下水位以下水饱和土层中固体骨架部分各形态波的标量势函数和矢量势函数分别为

则水饱和土中的总波场为

3）地下水位以上土层（气饱和土层）中．同理，地下水位以上气饱和土层中固体骨架部分各形态波的标量势函数和矢量势函数分别为

则气饱和土中的总波场为

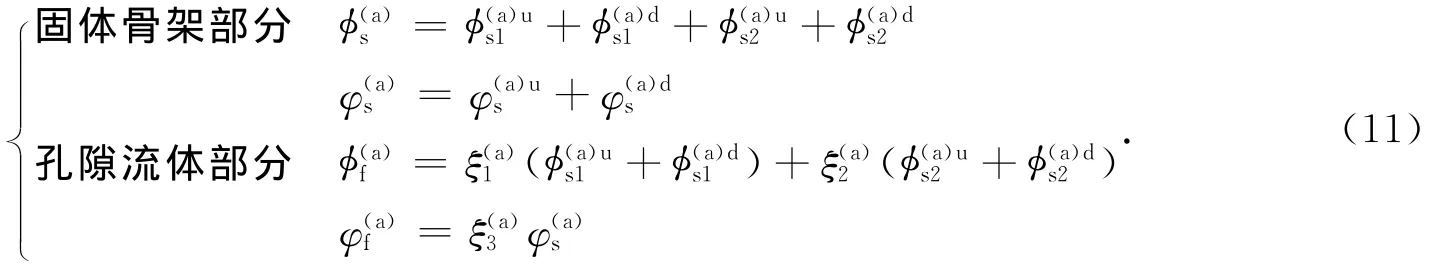
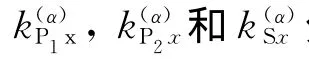
式 中 ，和分别为水或气饱和土中P1波、P2波和SV波的波速．具体计算方法参见Deresiewicz和Rice（1962）文章．

此外，根据Snell定理有

3 边界条件及问题的解

Deresiewicz和Skalak（1963）给出了两种不同饱和多孔介质交界面上的边界条件，后来其他研究人员根据不同需要进行了一系列修改（Lovera，1987；de la Cruz，Spanos，1989）．本文中，假设水气之间不存在质量交换，即不考虑气体在水相的溶解和溢出，则在水饱和土与气饱和土交界面上存在以下连续条件：

法向、切向总应力连续

孔隙流体压力连续

固体骨架法向、切向位移连续

流体法向位移连续

假定基岩与水饱和土层界面不透水，则基岩与水饱和土层交界面的边界条件可以表示为：

法向、切向总应力连续

水饱和土层固体骨架与基岩层法向、切向位移连续

水饱和土层固体骨架法向位移和流体位移连续

气饱和土表面为自由边界，其边界条件为

式中，上标“b”表示基岩，“s”表示饱和土中固相，“f”表示饱和土中流体相．

根据前面给出的各土层中的波场、单相弹性介质应力－应变关系、流体饱和多孔介质的应力－应变关系（式（3））以及上述边界条件（式（14）—（16）），可以得到P波（或SV波）从基岩层入射到含地下水的上覆土层时，在各土层中产生的波场的待定波幅系数为

式中，

4 地下水位变化对地面运动的影响分析

为便于分析，引入无量纲频率ω／ω1．其中ω1为地下水位在地表时的固有频率，地表位移用位移分量的幅值与入射波位移幅值u0的比值，即放大系数来表示．

取上覆土层总厚度H＝100m；基岩层材料参数ρb＝2 650kg／m3，λb＝μb＝5．3×109Pa；上覆土层中土颗粒的密度ρs＝2 700kg／m3，流固两相耦合质量密度ρ＝0；其它材料参数取值见表1．计算中考虑两组软硬程度不同的上覆土层：第一组上覆土层较软，土骨架剪切模量μ与孔隙水体积模量Kw比（土骨架的相对刚度）值为0．03；第二组上覆土层较硬，μ／Kw＝0．5．

把式（10）代入式（5），得到地表面水平位移幅值ux和竖向位移幅值uz为

表1 上覆土层的材料参数Table 1 The material parameters of the overlying soil

首先考虑P波入射的情况．图2给出了上覆土层取表1中第一组参数时，ω／ω1分别等于1．0，2．0和5．0时，不同地下水位（h1分别为0．1H，0．2H，0．3H和0．4H）条件下，地表水平位移和竖向位移放大系数随入射角变化的关系曲线．可以看出，当土骨架的相对刚度μ／Kw较小，即土骨架相对水来说很弱时，地下水位变化对地表位移放大系数影响较大，且这种影响与入射波频率和入射角有关．当相对频率ω／ω1较小（ω／ω1＝1．0）时，地下水位变化对x方向地表位移放大系数影响较大，随着入射角的增加，这种影响先增大后减小，对z方向地表位移放大系数影响较小；当相对频率ω／ω1较大（ω／ω1＝5．0）时，地下水位变化对x和z方向地表位移放大系数影响均较大．当波垂直入射时，随着地下水位的下降，z方向地表位移放大系数增加，h1＝0．4H时，z方向地表位移放大系数为h1＝0．1H时的4倍．

图2 P波入射下取第一组参数时地下水位变化对地表位移的影响Fig．2 Effects of groundwater level variation on ground motions for group 1parameters（P-wave）

为了更好地说明入射波频率的影响，图3给出了入射角为0°和30°时，不同地下水位条件下地表位移放大系数随相对频率ω／ω1变化的关系曲线．可以看出，地下水位的变化对地面运动的共振峰值和频率均有显著的影响．当入射角为0°（波垂直入射）时，随着地下水位的下降（气饱和土层厚度的增加），地面运动共振峰值逐渐增大，峰值频率逐渐减小；当入射角为30°（波斜入射）时，地下水位的变化对水平位移峰值频率影响相对较小，随着地下水位的下降，水平位移峰值基本呈增大趋势，但增大幅度较小．地下水位的变化对竖向位移峰值频率则影响较大，峰值频率随着地下水位降低逐渐减小，竖向位移峰值逐渐增大，但增幅逐渐减小．

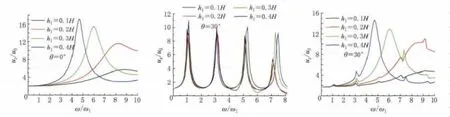
图3 P波入射下取第一组参数时不同地下水位下地表位移随相对频率变化的关系曲线Fig．3 x-and z-component of ground displacement amplitudes versus the relative frequencies under different groundwater levels for group 1parameters（P-wave）

产生这种现象的原因主要是随着地下水位的降低，上覆土层逐渐由水饱和变成气饱和．当取表1中第一组参数时，在水饱和土中，土骨架相对于水来说属于弱骨架；而在气饱和土中，土骨架相对于气体而言则为刚性骨架．这一变化对P1波影响很大，主要表现在P1波波速的差别上．表1给出了频率为10Hz时水饱和土和气饱和土中各波的波速．可以看出，当土层由水饱和变成气饱和时，P1波波速显著减小．

为了对比土骨架参数对结果的影响，图4给出了上覆土层取表1中第二组参数时，ω／ω1分别等于1．0，2．0和5．0时，不同地下水位条件下地表水平位移和竖向位移放大系数随入射角度变化的关系曲线．可以看出，当土骨架的相对刚度μ／Kw较大，即土骨架与水具有同等刚度时，地下水位变化对地表位移放大系数影响不大，且地表位移放大系数比μ／Kw较小时要小．这说明当土骨架刚度增加时，无论在水饱和还是气饱和土中土体骨架逐渐起主导作用，这时水饱和土与气饱和土中P1波波速相当，差别不大，具体如表1所示．

图4 P波入射下取第二组参数时地下水位变化对地表位移的影响Fig．4 Effects of groundwater level variation on ground motions for group 2parameters（P-wave）

对于SV波入射的情况，图5给出了取表1中第一组参数时，ω／ω1分别等于1．0，2．0和5．0时，地下水位变化对地表水平位移和竖向位移放大系数的影响．可以看出，SV波入射时地下水位变化对地表位移放大系数影响也较大，这种影响同样与入射波频率和入射角有关．由于篇幅有限，详细情况不再赘述．

5 讨论与结论

波在气饱和土中的传播与水饱和土中的传播差异较大，由此可以初步推断，地下水变化应该会对地震地面运动产生影响．但目前现有的场地反应问题研究中，大多以经典弹性动力学为理论依据，将天然土体简化为理想的各向同性单相介质进行分析，这一简化使得地下水的影响被忽略．

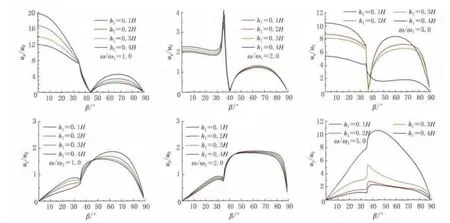
图5 SV波入射下取第一组参数时地下水位变化对地表位移的影响Fig．5 Effects of groundwater level variation on ground motions for group 1parameters（SV-wave）

本文以Biot（1956）提出的流体饱和多孔介质波动理论为基础，建立了成层地基模型，把地下水位以下的饱和土层用水饱和多孔介质模拟，地下水位以上土层用气饱和多孔介质模拟，得到了入射平面简谐波在成层地基中传播的解析解答．通过计算，分析了地下水位变化对地震地面运动的影响．得到如下结论：当土骨架的相对刚度较小，即土骨架相对水来说很弱时，地下水位变化对地表位移放大系数影响较大，随着地下水位的下降（气饱和土层厚度的增加），地面运动峰值逐渐增大，峰值频率逐渐减小；当土骨架的相对刚度较大，即土骨架与水具有同等刚度时，地下水位变化对地表位移放大系数影响不大．该结论说明对于软弱土层，地下水位变化对地震地面运动的影响应该引起重视．

诚然，地下水位的变化会引起土性质多方面的改变，但由于目前关于饱和土波动理论研究的限制，本文仅在弹性范围内假定地下水位下降时土的孔隙比不变的条件下，进行了初步探索，有一定局限性．地下水位变化对地震地面运动的影响尚有待进一步深入研究．

李伟华．2004．含饱和土的复杂局部场地波动散射问题的解析解和显式有限元数值模拟［D］．北京：北京交通大学土木建筑工程学院：230-233．

Li W H．2004．AnalyticalSolutionsandNumericalSimulationoftheScatteringofPlaneWavesbyLocalSiteswith SaturatedSoil［D］．Beijing：School of Civil Engineering and Architecture，Beijing Jiaotong University：230-233（in Chinese）．

刘晶波．1989．波动的有限元模拟及复杂场地对地震动的影响［D］．哈尔滨：国家地震局工程力学研究所：181-266．

Liu J B．1989．FiniteElementSimulationofWaveMotionandEffectofComplexSiteonSeismicWaveMotion［D］．Harbin：Institute of Engineering Mechanics，China Earthquake Administration：181-266（in Chinese）．

杨忠山，窦艳兵，王志强．2010．北京市地下水水位下降严重原因分析及对策研究［J］．中国水利，（19）：52-54．

Yang Z S，Dou Y B，Wang Z Q．2010．Analysis on the reasons of the decline of ground water level in the primary water supply source area of Beijing and the countermeasures［J］．ChinaWaterResources，（19）：52-54（in Chinese）．

周新民，夏唐代，徐平，邹振轩．2006．饱和土介质中地震波在水、气分界面上的反射与透射［J］．地震学报，28（4）：372-379．

Zhou X M，Xia T D，Xu P，Zou Z X．2006．Seismic reflection and transmission coefficients at an air-water interface of saturated porous soil［J］．ActaSeismologicaSinica，28（4）：372-379（in Chinese）．

Biot M A．1956．Theory of propagation of elastic waves in a fluid-saturated porous solid：Ⅰ．Low-frequency range［J］．JAcoustSocAm，28（2）：168-178．

Biot M A，Willis D G．1957．The elastic coefficients of the theory of consolidation［J］．JApplMech，24：594-601．

de la Cruz V，Spanos T J T．1989．Seismic boundary conditions for porous media［J］．JGeophysRes，94（B3）：3025-3029．

Deresiewicz H，Rice J T．1962．The effect of boundaries on wave propagation in a liquid-filled porous solid：Ⅲ．Reflection of plane waves at a free plane boundary（general case）［J］．BullSeismolSocAm，52（3）：595-625．

Deresiewicz H，Skalak R．1963．On uniqueness in dynamic poroelasticity［J］．BullSeismolSocAm，53（4）：783-788．

Eringen A C，Suhubi E S．1975．Elastodynamics，Vol．2：LinearTheory［M］．New York：Academic Press：1-14．

Lovera O C．1987．Boundary conditions for a fluid-saturated porous solid［J］．Geophysics，52（2）：174-178．

Trifunac M D．1972．Scattering of plane SH waves by a semi-cylindrical canyon［J］．IntJEarthqEngStructDyn，1（3）：267-281．