有限元三角网格中波动的频散分析及数值仿真

王圣柱 周建科 张奎华 王艺豪

1） 中国山东青岛266580中国石油大学（华东）地球科学与技术学院2） 中国山东东营257061中石化胜利油田西部新区研究院 3） 中国武汉430079武汉大学测绘学院



有限元三角网格中波动的频散分析及数值仿真

1） 中国山东青岛266580中国石油大学（华东）地球科学与技术学院2） 中国山东东营257061中石化胜利油田西部新区研究院 3） 中国武汉430079武汉大学测绘学院

波动问题有限元离散后会引起数值误差， 数值频散的本质就是数值误差传播引起的非物理解． 数值频散不仅没有实际意义， 而且还会影响对真实波动现象的认识． 为厘清有限元三角网格中波动数值频散的影响因素， 本文推导了集中质量矩阵和一致质量矩阵的频散函数， 同时给出了组合质量矩阵的频散函数， 并对不同质量矩阵的数值频散进行了对比研究． 理论分析和数值计算结果表明： 有限元三角网格中波动的数值频散受网格布局、 波传播方向、 单元网格纵横比以及质量矩阵的影响； 一致质量矩阵的数值频散比集中质量矩阵更易受到波传播方向的影响； 不合理的三角网格单元会对数值相速度（数值频散）产生不良影响； 正三角网格中波动的数值频散几乎不受波传播方向的影响； 一致质量矩阵与集中质量矩阵的线性组合能够有效地压制数值频散．

有限元法 三角网格 波动方程 数值频散 组合质量矩阵 数值仿真

引言

随着高性能计算机的不断发展， 有限元法在分析波的传播问题上得到广泛应用． 利用有限元方法模拟连续介质中的波动问题时， 需要将连续介质模型离散为网格模型， 这必然会引起精度上的误差， 使得具有不同频率的波动表现出不同的相速度（数值相速度）， 导致波场中出现伪波动， 即数值频散（董良国， 李培明， 2004； 吴国忱， 王华忠， 2005）． 因此， 网格离散引起的数值频散是影响波动方程数值计算精度的主要因素． 研究影响数值频散的因素， 对提高波动方程数值模拟的精度具有指导意义．

波动方程有限元数值解的频散分析要比有限差分法数值解的频散分析难得多（Marfurt， 1984； 李胜军等， 2008）， 这主要是因为有限元法具有多种网格剖分方式、 多种插值函数以及不同特性的质量矩阵（廖振鹏， 刘晶波， 1992； 薛东川等， 2007）， 这些因素都会对数值频散产生影响． 波动方程有限元数值解的频散问题一直是众多研究者研究的热点． 例如： Mullen和Belytschko（1982）最早对该问题进行研究， 考虑矩形网格以及不同形状的三角网格， 得出了矩形网格比三角网格具有更高精度的结论； 宗福开（1984）分析波动方程有限元数值解的频散特性， 给出了波动问题有限元离散化的准则， 并以几个典型实例来说明有限元法所能达到的精确程度； Abboud和Pinsky（1992）在三维网格单元下， 对声波方程有限元解的频散进行研究， 讨论了网格剖分及质量矩阵对数值频散的影响； 房营光和莫海鸿（2000）采用含有频率的高阶位移函数对有限元网格中波动的频散与稳定性条件进行了改进； 薛东川和王尚旭（2008）从数值模拟角度研究了一致质量矩阵和集中质量矩阵对数值频散的影响， 并采用二者的线性组合来压制数值频散； 此外， 波动方程谱元法数值解的频散特性（De Basabe， Sen， 2007； Seriani， Oliveira， 2008； Liuetal， 2012）以及间断有限元法数值解的频散特性（Huetal， 1999； Ainsworthetal， 2006； De Basabeetal， 2008； 贺茜君等， 2014）也得到了广泛研究．

本文针对有限元三角网格中波动的数值频散问题， 推导了集中质量矩阵和一致质量矩阵的频散函数， 通过频散曲线对比分析了不同质量矩阵的数值频散特性， 最后通过数值仿真对相关结论进行了验证．

1 有限元三角网格单元的波动方程

使用伽勒金法求解二维标量波动方程得到有限元方程组（杜世通， 1982）为

（1）

式中，Ke和Me分别为单元刚度矩阵和单元质量矩阵，u为单元节点位移列向量． 计算出每个单元的刚度矩阵和质量矩阵后， 集成为结构刚度矩阵K和结构质量矩阵M， 得到结构的有限元方程组为

（2）

式中U为结构节点位移列向量．

图1 三角网格单元示意图

图1给出了三角网格单元的示意图. 三角网格单元的3个顶点按逆时针顺序分别记为1， 2， 3， 其面积坐标可作如下定义（徐世浙， 1994）：

（3）

式中，a1=z3-z2，a2=z1-z3，a3=z2-z1，b1=x2-x3，b2=x3-x1，b3=x1-x2，c1=x3z2-x2z3，c2=x1z3-x3z1，c3=x2z1-x1z2，Δ=（a2b1-a1b2）/2为三角网格单元的面积． 可见，a1，a2，a3,b1,b2，b3,c1,c2，c3和Δ为只与单元节点坐标有关的常数， 因此L1，L2和L3是x和z的线性函数． 形函数矩阵N为

N=[L1L2L3]T,

（4）

则

（5）

三角网格单元的刚度矩阵Ke和一致质量矩阵Me分别为

（6）

（7）

（8）

对于式（2）， 时间因子采用二阶中心差分格式进行求解得到

（9）

式中Δt为时间采样间隔．

2 有限元三角网格中波动的数值频散函数

考虑图2a和图2b所示的网格结构， 假定区域为均匀、 无边界的， 且不考虑震源的加载． 图2a是在矩形单元上添加对角线形成的三角单元； 图2b则是在两条平行线之间以等腰三角单元进行剖分， 底边与x轴方向平行． 为了便于叙述， 将图2a和图2b所示的网格结构分别记为I类和Ⅱ类三角网格结构． 两种网格结构在x轴和z轴方向的采样间隔分别为Δx和Δz， 单元网格纵横比为γ=Δz/Δx． 图中带下标的大写字母为结构节点编号， 小写字母为单元编号， 阿拉伯数字为单元内节点编号．

图2 共点单元网格结构

2.1 Ⅰ类三角网格结构的频散函数

（10）

根据刚度（质量）矩阵的组装原理， 结构刚度矩阵K第J2行需要进行叠加计算的元素为

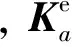
结构集中质量矩阵Ml第J2行的非零元素为

（12）

结构一致质量矩阵M第J2行的非零元素为

（13）

记节点J2的坐标为（mΔx，nΔz）， 根据平面波理论得到该点处的位移值um， n（孙成禹， 2007）为

um, n=Aexp[ik（mΔxcosθ+nΔzsinθ）-iωt],

（14）

式中，A为振幅，k为波数，ω为角频率，θ为波传播方向与x轴的夹角． 网格离散后的相速度cp为

（15）

对式（2）进行第J2行运算， 可以得到节点J2的位移与周围相关节点位移的关系．

2.1.1 集中质量矩阵的频散函数

在集中质量矩阵下， 对式（2）进行第J2行运算可以得到

um, nK（J2,J2）+um+1, nK（J2,K2）+um, n+1K（J2,J3）+um+1, n+1K（J2,K3）=0.

（16）

将式（11）、 （12）代入式（16）得到

（17）

再将式（14）代入式（17）， 整理得到

（18）

其中

（19）

在后续的推导中还会用到如下表达式：

（20）

最后将式（15）代入式（18）， 得到集中质量矩阵的频散函数为

（21）

2.1.2 一致质量矩阵的频散函数

同理对式（2）进行第J2行运算得到

2γ2（um-1, n+um+1, n）]=0.

（22）

仿照式（21）的推导过程， 可以得到一致质量矩阵的频散函数为

（23）

2.2 Ⅱ类三角网格结构的频散函数

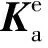
（24）

根据刚度（质量）矩阵的组装原理， 结构刚度矩阵K第J2行需要进行叠加计算的元素为

（25）

结构集中质量矩阵Ml第J2行的非零元素为

（26）

结构一致质量矩阵M第J2行的非零元素为

（27）

2.2.1 集中质量矩阵的频散函数

对式（2）进行第J2行运算可以得到

（28）

仿照式（21）的推导过程， 得到集中质量矩阵的频散函数为

（29）

2.2.2 一致质量矩阵的频散函数

同理对式（2）进行第J2行运算可以得到

（30）

仿照式（21）的推导过程， 得到一致质量矩阵的频散函数为

（31）

3 数值频散特性分析

根据奈奎斯特（Nyquist）频率可知， 当一个波长内空间采样点少于2个时会出现假频现象， 因此进行以下数值频散分析时，kΔx的取值范围为 0—π（孙成禹等， 2009； Liu， Sen， 2009）．

3.1 Ⅰ类三角网格结构中的频散特性分析

当θ取不同值（γ=1）时，cp/c与kΔx的关系如图3所示． 可以看出：

图3 θ取不同值时cp/c随kΔx的变化关系

1） 集中质量矩阵使相速度滞后于真实速度， 一致质量矩阵使相速度超前于真实速度， 二者对相速度起着相反的作用．

2） 随着传播角θ的增加， 一致质量矩阵的相速度比集中质量矩阵的相速度分散得更开， 即一致质量矩阵的数值频散比集中质量矩阵更易受到波传播方向的影响．

3） 无论是集中质量矩阵还是一致质量矩阵， 当kΔx的值接近于0时（空间采样间隔足够小），cp/c值几乎为1， 此时数值频散能够得到较好地压制， 且几乎不受波传播方向的影响．

4） 如果认为当所有传播方向上的频散误差R=|1-cp/c|×100% ≤0.5%时， 可以忽略数值频散的影响， 则集中质量矩阵满足该不等式的条件是kΔx≤0.3481， 即单元网格的最大边长Δxmin应该小于或等于λ/20（λ为波长）； 一致质量矩阵下满足该不等式的条件是kΔx≤0.2291， 即Δxmin≤λ/27． 因此， 对空间采样间隔而言， 集中质量矩阵压制数值频散的效率比一致质量矩阵的高．

下面研究单元网格纵横比γ和波传播方向θ对数值频散的影响． 假定kΔx=π/2， 图4给出了当γ取不同值时cp/c与θ的关系． 可以看出：

1） 在空间采样间隔不是足够小的情况下， 数值频散因波传播方向的不同而发生显著的变化， 且这种变化是周期性的． 在集中质量矩阵下， 当γ=1时， 周期为π/2， 以π/4+kπ/2（k=0， 1， 2， 3, …）为对称轴； 当γ≠1时， 相应的周期为π， 对称轴为π/2+kπ（k=0， 1， 2， 3, …）． 在一致质量矩阵下， 周期均为π， 在周期内不具有对称性．

图4 γ取不同值时cp/c随θ的变化关系

2） 当θ较小时， 集中质量矩阵的数值频散几乎不受单元网格纵横比的影响， 而一致质量矩阵的数值频散则不具有此特性．

3） 在集中质量矩阵下（γ=1）， 当波沿水平方向（θ=0°）和垂直方向（θ=90°）传播时， 其数值频散最严重； 当波沿θ=45°方向传播时， 其数值频散最小（图4a中的γ=1.0曲线）， 且水平方向的数值频散不受单元网格纵横比的影响， 即通过减小单元网格纵横比来压制数值频散不是一种行之有效的方法．

4） 在一致质量矩阵下， 水平方向的数值频散也不受单元网格纵横比的影响．

3.2 Ⅱ类三角网格结构中的频散特性分析

仍然假定kΔx=π/2， 其数值频散cp/c与θ及γ的关系分别如图5和图6所示． 可以看出：

1） 在集中质量矩阵下， 当单元网格纵横比γ<0.5时， 得到了相速度有可能大于介质真实速度的结果， 该结果与集中质量矩阵使相速度滞后于真实速度相反． 进一步分析可以发现， 当γ=0.5时， 三角网格单元为等腰直角三角形； 当γ<0.5时， 三角网格单元为等腰钝角三角形． 因此不难发现在集中质量矩阵下， 出现相速度大于介质真实速度的原因是单元剖分不合理， 出现了钝角三角单元， 影响数值计算的精度． 同理， 当单元剖分不合理时， 一致质量矩阵的相速度突变得非常大， 对数值频散会产生不良影响． 因此， 对这类网格结构而言， 选择合适的网格纵横比至关重要， 一定要避免出现过锐或过钝的三角单元．

图5 γ取不同值时cp/c随θ的变化关系. （a） 集中质量矩阵； （b） 一致质量矩阵

图6 θ取不同值时cp/c随γ的变化关系. （a） 集中质量矩阵； （b） 一致质量矩阵

2） 在该类网格结构下， 两种质量矩阵的数值频散具有相同的周期性及对称性．

3） 当单元网格纵横比为0.866时， 不同传播方向上的数值频散几乎相等（图6中所有曲线的交点）， 此时三角网格单元为正三角形．

图7中的γ=0.866曲线和图8a分别展示了当单元为正三角形时数值频散与波传播方向及空间采样间隔的关系． 可以看出， 图7中的γ=0.866曲线周期为π/3， 即正三角网格下的周期由π变成了π/3， 因为正三角网格下的结构只需旋转π/3就不会发生变化． 图8a中的曲线基本重合， 也进一步证实了正三角单元下的数值频散几乎不受波传播方向的影响. 图8b则为单元网格纵横比为0.4时数值频散与空间采样间隔的关系． 可以看出， 在集中质量矩阵下， 当波沿水平方向及其附近传播时， 随着空间采样间隔的增加， 出现了相速度大于介质真实速度的现象， 且一致质量矩阵的相速度变得非常大．

图7 γ取不同值时cp/c随θ的变化关系. （a） 集中质量矩阵； （b） 一致质量矩阵

图8 θ取不同值时cp/c随kΔx的变化关系

3.3 一致质量矩阵与集中质量矩阵的线性组合对数值频散的影响

（32）

式中α为组合系数， 则Ⅰ类网格结构的组合质量矩阵频散函数可以表示为

（33）

Ⅱ类网格结构的组合质量矩阵频散函数可以表示为

（34）

当组合系数α=1时， 组合质量矩阵的频散函数变为一致质量矩阵的频散函数； 当α=0时， 组合质量矩阵的频散函数变为集中质量矩阵的频散函数． 对于Ⅰ类网格结构， 当组合系数α=0.5、 单元网格纵横比γ=1时， 组合质量矩阵的数值频散与空间采样间隔的关系如图9a所示； Ⅱ类网格结构的组合系数α也取为0.5、 单元网格为正三角形时， 组合质量矩阵的数值频散与空间采样间隔的关系如图9b所示．

图9 θ取不同值时cp/c随kΔx的变化关系

Ⅰ类网格结构采用组合质量矩阵后， 整体上数值频散得到有效地压制， 但某些传播方向上的数值频散也会增加． 例如图9a中π/4方向上的数值频散， 当kΔx=2时， 频散误差为10.1%， 而采用集中质量矩阵时， 相应的频散误差为8.1%． 此外， 还应注意到当采用组合质量矩阵后， 在某些传播方向上相速度小于介质的真实速度， 而在另一些传播方向上， 相速度则大于介质的真实速度， 这意味着相速度失去向真实速度收敛的单调性．

对于Ⅱ类网格结构（γ=0.866）， 采用组合质量矩阵后，cp/c接近于1的范围得到显著地延伸（图9b）． 同样认为当所有传播方向上的频散误差R≤0.5%时， 可以忽略数值频散的影响， 则在组合质量矩阵下kΔx≤1.421， 即一个波长内所包含的空间采样点不应少于5个； 而单独采用集中质量矩阵或一致质量矩阵时， 相应的采样点不应少于15个． 最后取kΔx=π/2， 两种网格结构的部分数值频散如表1所示．

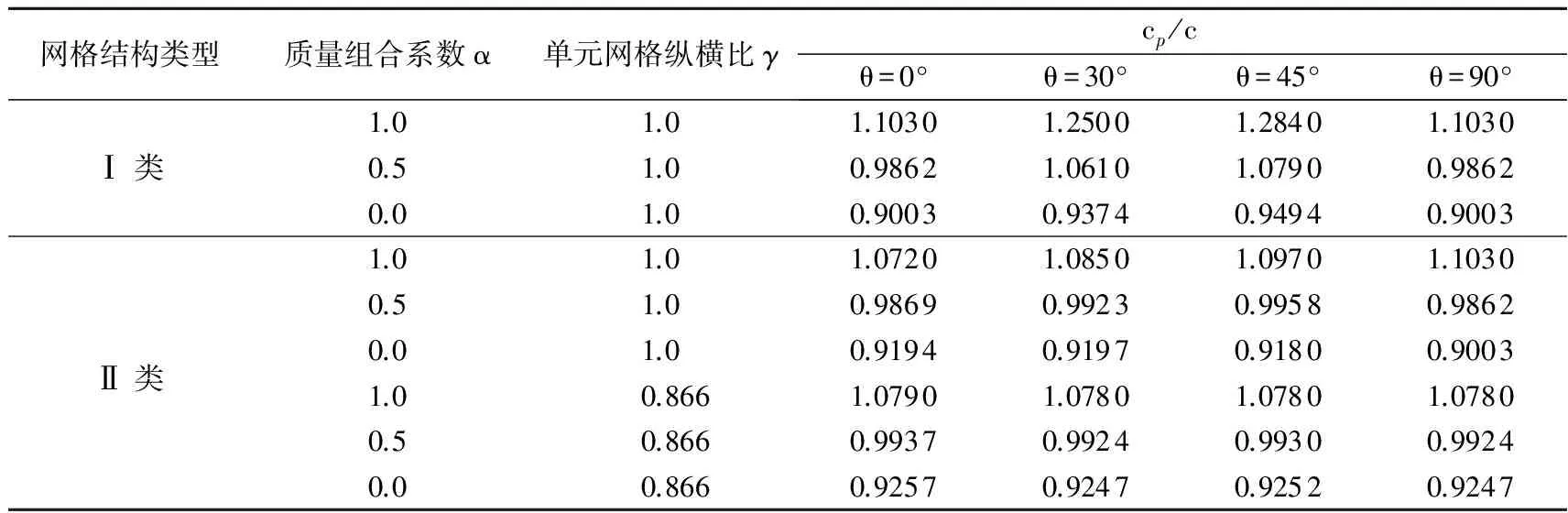
表1 kΔx=π/2时的频散cp/cTable 1 Dispersion cp/c at kΔx=π/2

4 数值仿真

由式（9）可知， 用有限元法解波的传播问题时， 需要在时间递推过程中求解大型稀疏方程组． 结构一致质量矩阵M是大型稀疏矩阵， 对其求逆不仅需要占用大量机时， 而且引入数值计算误差的可能性也增大； 而结构集中质量矩阵Ml是一对角矩阵， 在求解式（9）时， 也就避免了大型稀疏矩阵的求逆运算． 因此， 本文的数值仿真采用集中质量矩阵． 考虑纵波波速c=2.0 km/s的均匀介质模型， 计算区域为1.8 km×1.8 km， 震源采用主频为33 Hz的雷克子波， 位于模型中央． 两种网格结构的空间横向采样间隔Δx均为6 m， 时间采样间隔Δt=0.5 ms， 改变单元网格纵横比γ， 得到0.43 s时刻的波场快照如图10所示． 图10a （γ=1）和图10b （γ=0.3）为在Ⅰ类网格结构下得到的波场快照． 可以看出: 当单元网格纵横比γ=1时， 数值频散在θ=0°时最大， 且随着θ的增大而减小， 在θ=45°时最小， 这与图4a中的γ=1.0曲线一致； 将单元网格纵横比减小到0.3时， 只有当θ≥45°时， 数值频散才得到有效地压制． 在Ⅱ类网格结构下得到的波场快照分别如图10c （γ=1）、 图10d （γ=0.866）、 图10e （γ=0.5）和图10f （γ=0.3）所示． 可以看出： 当单元网格纵横比由1减小到0.866时， 数值频散在一定程度上得到减弱， 且此时各个传播方向上的数值频散基本一致； 当单元网格纵横比减小到0.5时， 频散压制效果尤为明显； 当单元网格纵横比减小到0.3时， 在水平方向附近出现相速度大于介质真实速度的现象． 以上数值仿真结果均与理论分析一致．

图10 不同条件下的数值频散现象（0.43 s）

Fig.10 The numerical dispersion under different conditions （0.43 s）

（a） Ⅰ类网格结构（γ=1）; （b） Ⅰ类网格结构（γ=0.3）; （c） Ⅱ类网格结构（γ=1）;（d） Ⅱ类网格结构（γ=0.866）; （e） Ⅱ类网格结构（γ=0.5）; （f） Ⅱ类网格结构（γ=0.3）

（a） Mesh structure Ⅰ（γ=1）; （b） Mesh structure Ⅰ（γ=0.3）; （c） Mesh structure Ⅱ（γ=1）;（d） Mesh structure Ⅱ（γ=0.866）; （e） Mesh structure Ⅱ（γ=0.5）; （f） Mesh structure Ⅱ（γ=0.3）

5 结论

本文研究了有限元三角网格中不同质量矩阵下波动的数值频散特性， 得到如下结论：

1） 在非钝角三角网格中， 集中质量矩阵使数值相速度滞后于真实速度， 一致质量矩阵使数值相速度超前于真实速度．

2） 一致质量矩阵的数值频散比集中质量矩阵更易受到波传播方向的影响．

3） 在Ⅰ类三角网格结构中， 水平方向（θ=0°）的数值频散不受单元网格纵横比的影响， 集中质量矩阵与一致质量矩阵的线性组合可以减弱大部分传播方向上的数值频散， 但在某些传播方向上， 数值频散反而增加； 此外， 采用组合质量矩阵后， 因传播方向的不同， 相速度有可能小于介质的真实速度， 也有可能大于介质的真实速度．

4） 在Ⅱ类三角网格结构中， 过锐或过钝的三角单元不仅会导致集中质量矩阵的相速度大于介质的真实速度， 而且还会使一致质量矩阵的相速度变得异常的大， 对数值解的精度产生不良影响， 甚至会导致错误的结果， 而正三角单元中的数值频散受波传播方向的影响较小． 因此在网格剖分中， 单元的形状接近等边三角形最好， 不宜过锐或过钝． 在保证三角单元非过锐或过钝的前提下， 减小单元网格纵横比可以显著地压制各个传播方向上的数值频散．

5） 在正三角网格结构中采用组合质量矩阵后， 有效压制数值频散的最大空间采样间隔可以得到显著增加， 且不会出现相速度在某些传播方向上小于介质的真实速度， 而在另一些传播方向上大于介质真实速度的现象．

董良国， 李培明. 2004. 地震波传播数值模拟中的频散问题[J]. 天然气工业， 24（6）: 53--56.

Dong L G， Li P M. 2004. Dispersive problem in seismic wave propagation numerical modeling[J].NaturalGasIndustry， 24（6）: 53--56 （in Chinese）.

杜世通. 1982. 变速不均匀介质中波动方程的有限元法数值解[J]. 华东石油学院学报， 6（2）: 1--20.

Du S T. 1982. Finite element numerical solution of wave propagation in non-homogeneous medium with variable velocities[J].JournalofEastChinaPetroleumInstitute， 6（2）: 1--20 （in Chinese）.

房营光， 莫海鸿. 2000. 有限元网格中波动的频散与稳定性的一种改进方法[J]. 地震工程与工程振动， 20（1）: 21--26.

Fang Y G， Mo H H. 2000. An improved method for dispersion and stability of wave motion in finite element meshes[J].EarthquakeEngineeringandEngineeringVibration， 20（1）: 21--26 （in Chinese）.

贺茜君， 杨顶辉， 吴昊. 2014. 间断有限元方法的数值频散分析及其波场模拟[J]. 地球物理学报， 57（3）: 906--917.

He X J， Yang D H， Wu H. 2014. Numerical dispersion and wave-field simulation of the Runge-Kutta discontinuous Galerkin method[J].ChineseJournalofGeophysics， 57（3）: 906--917 （in Chinese）.

李胜军， 孙成禹， 高建虎， 刘军迎. 2008. 地震波数值模拟中的频散压制方法分析[J]. 石油物探， 47（5）: 444--448.

Li S J， Sun C Y， Gao J H， Liu J Y. 2008. Analysis of dispersion suppression in wave equation numerical simulation[J].GeophysicalProspectingforPetroleum， 47（5）: 444--448 （in Chinese）.

廖振鹏， 刘晶波. 1992. 波动有限元模拟的基本问题[J]. 中国科学： B辑， 22（8）: 874--882.

Liao Z P， Liu J B. 1992. The basic problems of wave motion with finite element simulation[J].ScienceinChina:SeriesB， 22（8）: 874--882 （in Chinese）.

孙成禹. 2007. 地震波理论与方法[M]. 东营: 中国石油大学出版社: 31--37.

Sun C Y. 2007.TheoryandMethodsofSeismicWaves[M]. Dongying: China University of Petroleum Press: 31--37 （in Chinese）.

孙成禹， 宫同举， 张玉亮， 张文颖. 2009. 波动方程有限差分法中的频散与假频分析[J]. 石油地球物理勘探， 44（1）: 43--48.

Sun C Y， Gong T J， Zhang Y L， Zhang W Y. 2009. Analysis on dispersion and alias in finite-difference solution of wave equation[J].OilGeophysicalProspecting， 44（1）: 43--48 （in Chinese）.

吴国忱， 王华忠. 2005. 波场模拟中的数值频散分析与校正策略[J]. 地球物理学进展， 20（1）: 58--65.

Wu G C， Wang H Z. 2005. Analysis of numerical dispersion in wave-field simulation[J].ProgressinGeophysics， 20（1）: 58--65 （in Chinese）.

徐世浙. 1994. 地球物理中的有限单元法[M]. 北京: 科学出版社: 39--42.

Xu S Z. 1994.FiniteElementMethodforGeophysics[M]. Beijing: Science Press: 39--42 （in Chinese）.

薛东川， 王尚旭， 焦淑静. 2007. 起伏地表复杂介质波动方程有限元数值模拟方法[J]. 地球物理学进展， 22（2）: 522--529.

Xue D C， Wang S X， Jiao S J. 2007. Wave equation finite-element modeling including rugged topography and complicated medium[J].ProgressinGeophysics， 22（2）: 522--529 （in Chinese）.

薛东川， 王尚旭. 2008. 利用组合质量矩阵压制数值频散[J]. 石油地球物理勘探， 43（3）: 318--320.

Xue D C， Wang S X. 2008. Using combined mass matrix to suppress numeric dispersion[J].OilGeophysicalProspecting， 43（3）: 318--320 （in Chinese）.

宗福开. 1984. 波传播问题中有限元分析的频散特性及离散化准则[J]. 爆炸与冲击， 4（4）: 16--23.

Zong F K. 1984. Frequency-dispersion characteristics and discretization of the finite element analysis in wave propagation problems[J].ExplosionandShockWaves， 4（4）: 16--23 （in Chinese）.

Abboud N N， Pinsky P M. 1992. Finite element dispersion analysis for the three-dimensional second-order scalar wave equation[J].IntJNumerMethodsEng， 35（6）: 1183--1218.

Ainsworth M， Monk P， Muniz W. 2006. Dispersive and dissipative properties of discontinuous Galerkin finite element methods for the second-order wave equation[J].JSciComput， 27（1/2/3）: 5--40.

De Basabe J D， Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations[J].Geophysics， 72（6）: T81--T95.

De Basabe J D， Sen M K， Wheeler M F. 2008. The interior penalty discontinuous Galerkin method for elastic wave pro-pagation: Grid dispersion[J].GeophysJInt， 175（1）: 83--93.

Hu F Q， Hussaini M Y， Rasetarinera P. 1999. An analysis of the discontinuous Galerkin method for wave propagation problems[J].JComputPhys， 151（2）: 921--946.

Liu T， De Basabe J D， Li L， Hu T Y， Sen M K， Wei X C. 2012. Grid dispersion and stability of the spectral element method with triangular elements[C]∥82thAnnualInternationalMeeting，SEG，TechnicalProgramExpandedAbstracts. Las Vegas： Society of Exploration Geophysicists: 1--5.

Liu Y， Sen M K. 2009. A new time-space domain high-order finite-difference method for the acoustic wave equation[J].JComputPhys， 228（23）: 8779--8806.

Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J].Geophysics， 49（5）: 533--549.

Mullen R， Belytschko T. 1982. Dispersion analysis of finite element semidiscretizations of the two-dimensional wave equation[J].IntJNumerMethodsEng， 18（1）: 11--29.

Seriani G， Oliveira S P. 2008. Dispersion analysis of spectral element methods for elastic wave propagation[J].WaveMotion， 45（6）: 729--744.

Dispersion analysis and numerical simulation of wave motion in finite element algorithm with triangular meshes

1）SchoolofGeosciences，ChinaUniversityofPetroleum，ShandongQingdao266580，China2）WesternNewProspectResearchInstitute，ShengliOilfieldCompany，SINOPEC，ShandongDongying257061，China3）SchoolofGeodesyandGeomatics，WuhanUniversity，Wuhan430079，China

The finite element discretization of wave motion can cause numerical error. The numerical dispersion is in essence the non-physical solution caused by the propagation of numerical error. Not only has the numerical dispersion no practical meaning， but also it can affect the understanding of real fluctuations. In order to clarify the influence factors of numerical dispersion in finite element algorithm with triangular meshes， the dispersion functions of lumped mass matrix and consistent mass matrix are derived respectively， and the dispersion function of combined mass matrix is also given. And then the numerical dispersion of different mass matrices are compared. The results of theoretical analysis and numerical simulation indicate: ① The numerical dispersion in finite element algorithm with triangular meshes depend on the mesh layout， direction of wave propagation， the ratio of vertical length to horizontal length and the mass matrix; ② The numerical dispersion of consistent mass marix is more easily affected by wave propagation direction than that of lumped mass matrix; ③ The irrational triangular meshes have a bad effect on numerical phase velocity （numerical dispersion）; ④ Equilateral triangular meshes can provide superior results regardless of the propagation direction; ⑤ The linear combination of lumped mass matrix and consistent mass matrix can effectively suppress numerical dispersion.

finite element method; triangular mesh; wave equation; numerical dispersion; combined mass matrix; numerical simulation

10.11939/jass.2015.03.012.

国家“十二五”重点科技攻关项目（2011ZX05002-002）与中石化科技重大攻关项目（P13020）联合资助.

2014-05-25收到初稿， 2014-08-08决定采用修改稿.

e-mail: pillar1979@163.com

10.11939/jass.2015.03.012

P315.3+1

A

王圣柱, 周建科, 张奎华, 王艺豪. 2015. 有限元三角网格中波动的频散分析及数值仿真. 地震学报, 37（3）: 493--507.

Wang S Z, Zhou J K, Zhang K H, Wang Y H. 2015. Dispersion analysis and numerical simulation of wave motion in finite element algorithm with triangular meshes.ActaSeismologicaSinica, 37（3）: 493--507. doi:10.11939/jass.2015.03.012.