基于产品差异的研发补贴、技术溢出与研发投入研究

□张 伟 仲伟俊 梅姝娥

[东南大学 南京 211189]

基于产品差异的研发补贴、技术溢出与研发投入研究

□张 伟 仲伟俊 梅姝娥

[东南大学 南京 211189]

考虑到政府对企业技术创新的激励政策、研发过程中的技术溢出以及产品差异化，建立了两个生产有差异化产品竞争企业的技术创新投入模型。首先不考虑时间因素得出了古诺竞争情形下的生产数量、利润以及研发投入的均衡解，社会福利最大化条件下的最优研发补贴以及最优研发补贴存在的条件；并对研发补贴、技术溢出、产品差异化与研发投入之间的关系进行了分析。研究表明企业间产品差异较小且研发补贴不多时，研发投入与技术溢出成负相关关系；企业间产品差异较大且研发补贴较多时，技术溢出与研发投入成正相关关系。然后考虑到企业间研发成功的时间不同，把利息引入模型分析了产品差异化、技术溢出、研发补贴对研发成功时间的影响，并得出了社会福利最大化的最优条件。

技术溢出；研发补贴；产品差异化；研发投资；研发时间

引言

随着经济全球化和科学技术的迅速发展，新技术革命正在发生，竞争方式也在发生巨大变化，顾客对产品要求也越来越高，这就要求企业在管理中不断创新，同时进行技术创新。另外，随着现在市场上产品的多样化和复杂化程度的提高，产品之间的差异化程度也在不断接近，这就要求生产有差异化产品的企业必须进行创新，以获得各自的竞争优势，从而占领市场的一席之地。技术创新过程中，由于研发企业在进行R&D投资时，不能排除其他企业通过各种渠道（如技术交流、产品信息发布以及R&D人员流动等）使用R&D投资产生的技术知识而获得收益，且不必为此支付费用，从而产生了技术溢出效应。技术溢出在促进其他企业研发水平提高的同时，对研发企业自身没有任何回报。企业间的溢出效应不仅影响企业的研发决策还影响到社会福利，政府为了激励创新企业进行研发创新，会采取一些措施（如给予研发补贴、减少税收）鼓励企业积极进行创新，从而使社会福利达到最大。

国内外学者考虑到技术溢出、研发补贴等因素，对企业的研发投资决策做了一些研究。d'Aspremont 和Jacquemin通过建立两阶段双寡头博弈模型，最早研究了技术溢出时两同质企业在古诺竞争市场结构下的研发投资策略以及最优R&D投入水平[1]。基于AJ模型，Hinloopen假设政府在企业研发之前以最大化社会福利为目标选择最优的研发成果补贴率，其中补贴来源于事后的产品征税[2]。他指出，补贴不仅可以刺激企业从事更多的R&D投资，而且还可以提高整个社会的福利水平。这表明了对R&D成果进行补贴确实可以在某种程度上改善R&D活动在市场机制内的失灵。Hinloopen指出上述结论在投资溢出下也是成立的[3]。Hinloopen又将研究扩展到多寡头古诺竞争和伯川德竞争市场[4]。Piga研究了技术溢出、企业的位置选择与产品差异之间的关系，研究表明企业所在位置之间的距离随着产品差异化程度的增大而增加[5]。Tesoriere对生产同一种产品的两个垄断企业技术研发的溢出性进行了研究，他假设同时研发时溢出为零、有顺序研发时溢出不为零的前提下，在同时研发、有顺序研发两种情况分别求出了两个对称企业在古诺竞争环境下研发投入的均衡解 。Hinloopen在投资溢出下比较了古诺均衡和伯川德均衡的动态效率[7]。Petrakis和Sandonís评估了创新的补贴、鼓励研发政策以及其他反垄断措施对提高社会福利的效果[8～9]。Fjell和Heywood讨论了混合多寡头模型中的私有企业的角色变化时，研发补贴与研发产出、社会福利之间的变化关系，以及研发补贴对企业研发决策的影响[10]。José Gil-Moltó和Poyago-Theotoky对有研发补助和无研发补助两种情形下，分别对生产同一种产品的混合双寡头和纯私企双寡头在技术研发时的技术溢出、研发补贴、私有化、社会福利之间关系进行了研究，这是第一篇研究研发补贴对混合双寡头影响的文章，但是文中研究的是生产同一种产品的两个竞争企业[11]。Saha分析了生产产品有差异的对称混合双寡头企业的最佳私有程度，产品差异性对私有企业的影响，并提出了最优税收补贴政策来替代私有化[12]。Milliou[13]与Pal[14]研究了生产有差异化产品的两个企业面临市场上同一种技术，在古诺竞争环境与伯川德竞争环境下，产品差异率对采纳时间选择的影响，但文中没有考虑到技术创新过程中的学习、溢出等因素。国内方面，胡荣利用非线性动力系统的分支理论，研究了分别具有有限理性和简单理性的双寡头R&D竞争模型，进一步通过对模型的解析分析和数值仿真，研究了技术溢出对双寡头R&D竞争演化的影响[15]。生延超在同质双寡头古诺竞争下比较了创新投入补贴和创新产品补贴的效果[16]。方海燕基于产品差异性与伯川德（价格）竞争在多种研发合作方式下研究了政府的最优R&D补贴策略[17]。韦铁在技术溢出情形下对中小企业的自主创新投入问题进行了研究[19]。

尽管已有文献讨论了技术溢出对研发投资和社会福利的影响、产品差异化对技术创新时间影响等问题，但有的文献中忽视了政府的激励政策和研发时间，有的文献中忽视了产品之间的替代性即产品差异化。本文与José Gil-Moltó和Poyago-Theotoky[11]区别是考虑到了产品之间的替代性即产品差异化、研发时间；与Milliou[13]、Pal[14]的区别是考虑到技术创新过程中的学习、溢出等因素；与Saha[1 7]、方海燕[12]不同的是，本文考虑到技术的研发时间。在上述文献的基础上，本文考虑到政府的研发补贴、企业间的技术溢出、产品差异等因素，建立了三阶段博弈模型，对生产有差异化产品的两个竞争企业的创新研发投资和研发成功时间进行了分析，重点分析了产品差异化、技术溢出的存在以及政府给予的补贴对企业研发创新的影响，另外还给出了社会福利最大化时的最优补贴。

一、模型框架

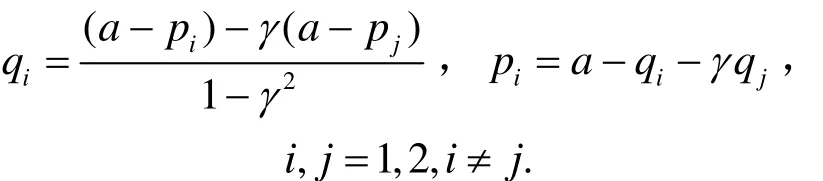
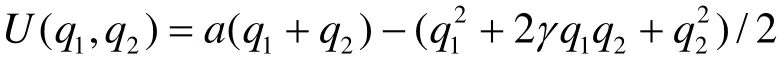
为了社会福利和收益最大，政府鼓励企业进行研发，对研发企业实施研发补贴政策，每一单位的研发产出，政府给予研发补贴s，则企业i的补贴为所以企业的最大利润可表示为：

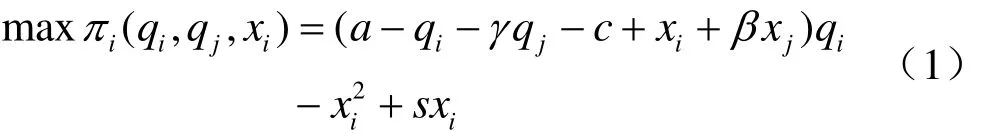
本文中企业间的竞争博弈分为三个阶段：第一阶段政府选择给予研发补贴以使得社会福利最大；第二阶段，企业选择对技术进行研发投入；第三阶段两企业对产量进行的博弈阶段即古诺竞争阶段。在此利用逆序归纳法求解。

二、古诺竞争情形下研发补贴、技术溢出与研发投入关系分析

现在考虑两企业进行技术创新研发和产量竞争的三阶段博弈，第一阶段政府选择给予研发补贴以使得社会福利最大，第二阶段为非合作、降低成本的技术创新投入博弈，第三阶段为产量博弈，即古诺博弈。下面利用逆序归纳法求得各种情形下的解。

首先在第三阶段，根据企业的反需求函数和式（1），可得企业 ,i j各自均衡产量和利润分别为：

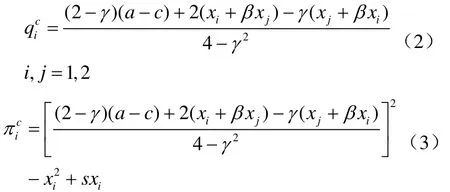
在第二阶段，企业进行研发创新投入竞争的博弈，根据各自企业的研发水平和溢出，可得出各企业研发产出的反应函数为：

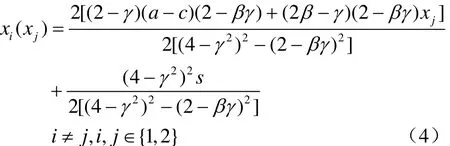
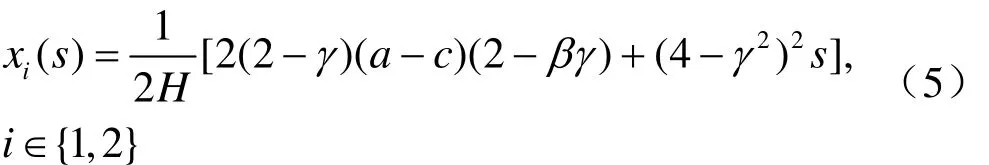
将式（5）代入式（2），可以得到均衡情形下，均衡产出关于研发补贴的函数表达式为：

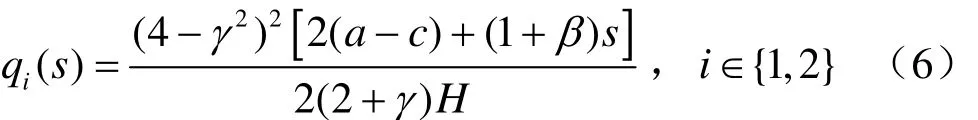
由于企业在市场竞争环境中自发的创新投入水平与社会最优的创新投入水平相比较是偏低的。因此，为了社会福利最大化，政府鼓励企业进行创新研发，并且给予企业研发补贴予以支持。社会福利SW包括消费者剩余、生产者剩余以及净研发补贴，表示为[11]：

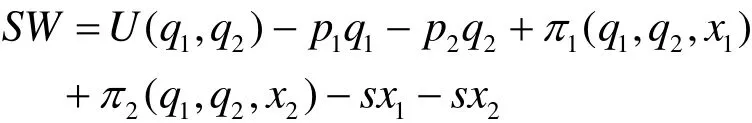
将式（1）～（6）代入上式，可得社会福利SW为：

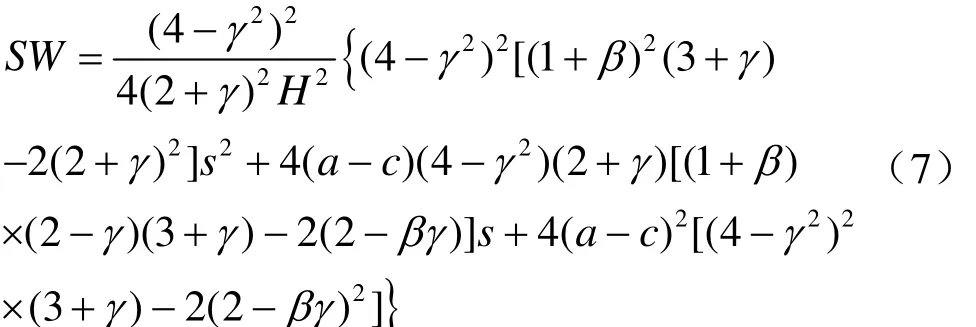
在第一阶段政府选择给予企业研发补贴予以支持以使得社会福利达到最大，此时可求得最优研发补贴为

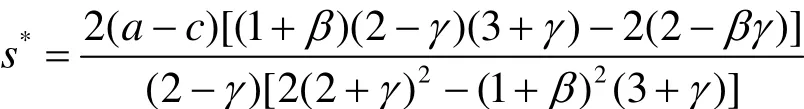
将式（5）视为γ的函数，求偏导得：

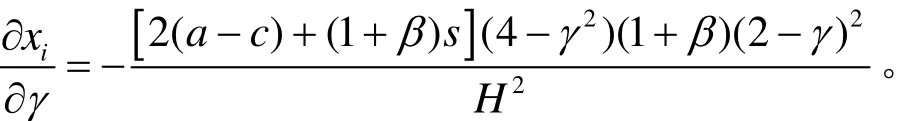
所以，对于两个生产有差异化产品的企业，在存在技术溢出和研发补贴时，企业研发投入随着创新产品差异率的增大而降低，研发投入随着产品差异率的减少而增加。也就是说，企业产品差异越大，γ越小，企业独立创新的空间就越大，它们之间进行合作创新的空间就越小，此时技术溢出对企业的创新有利，可以达到双赢的效果，又由于研发补贴的存在，企业会增加研发投入。反之，γ越大，企业之间的创新产品越接近，企业独立创新的空间就越小，它们之间进行合作创新的空间就越大，此时技术溢出对企业的创新不利，企业会减少研发投入。

结论1 在存在技术溢出和政府研发补贴时，两个生产有差异化产品企业的研发投入随着研发补贴的增加，企业会增大研发投入。

证明：将式（5）视为β的函数，求偏导得：

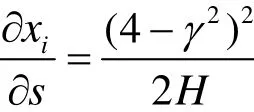
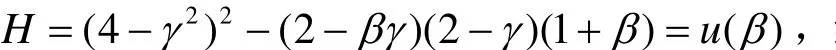
令经过整理可变形为

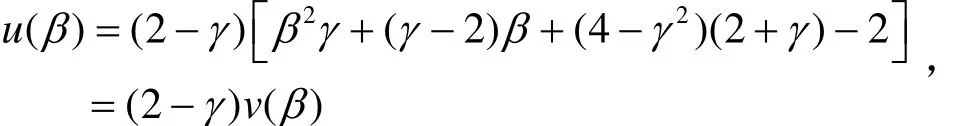
其中

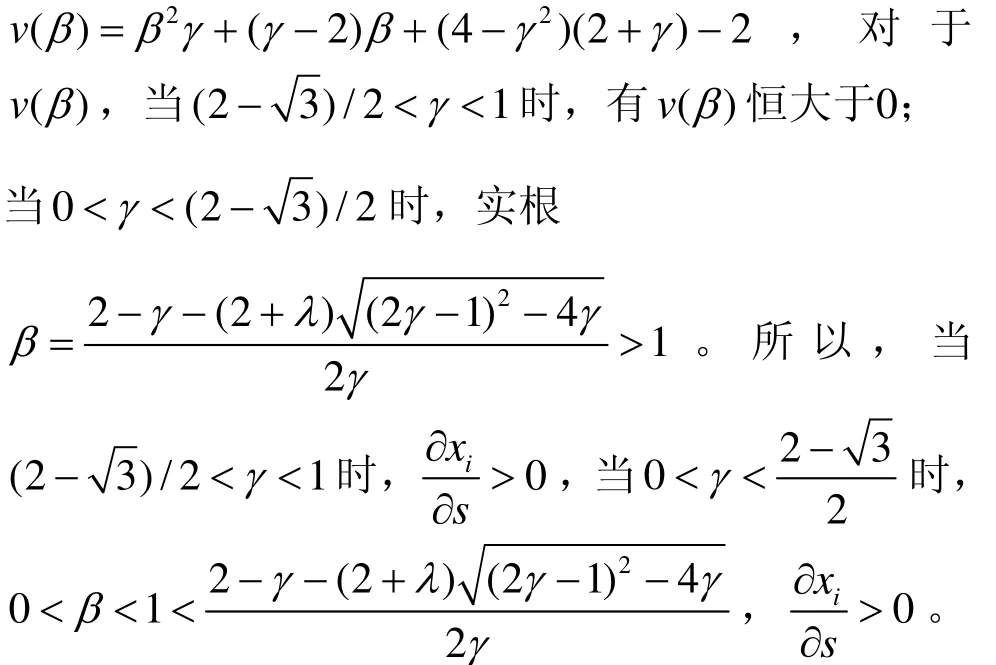
结论1表明：随着产品研发补贴的增加，研发补贴可以抵消因技术溢出而减少的企业研发边际成本，企业对研发投入也会增加。反之，政府研发补贴如果降低，企业在研发时又存在技术溢出，企业对产品创新研发的投入会减少。

结论2 两个生产有差异化产品的企业在投资研发创新时，如果两企业的产品差异不大（0.43141γ＜＜），并且政府给予企业的研发补贴不多时，技术溢出与两竞争企业的研发投入成反方向关系。即技术溢出越大，研发投入越少，技术溢出越小，研发投入越多。如果企业的产品差异较大并且政府给予企业的研发补贴较多时，技术溢出与企业创新投入呈正方向变化，即技术溢出越大，创新投入越大，此时技术溢出对企业创新投入有利。其中

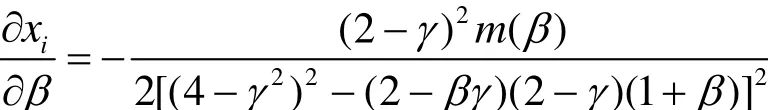
证明：由式（7）可得：

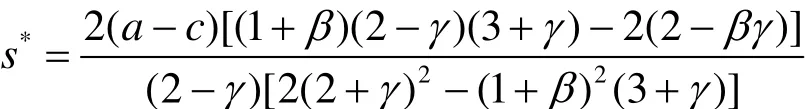
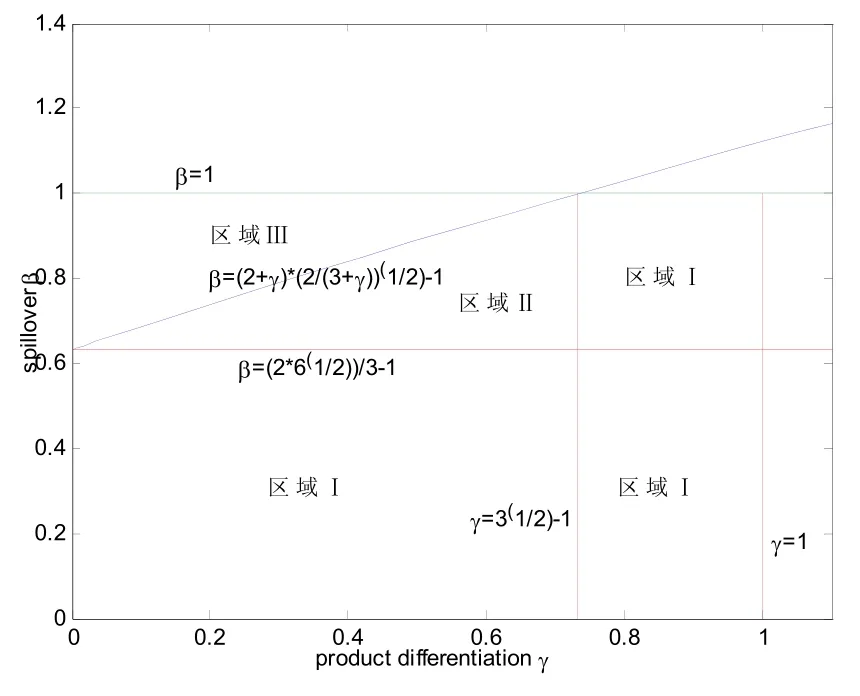
图1 最优研发补贴的存在性区域分析

当企业间产品的差异较小（γ较大）时，企业之间的研发竞争程度增大，为了占据市场竞争优势，企业会自主进行研发。同时由于企业在市场竞争环境中自发的创新投入水平与社会最优的创新投入水平相比较是偏低的，因此，为了社会福利最大化，政府会给予一定研发补贴予以激励，此时研发补贴有最优解，并且最优研发补贴随着产品差异化的减小（γ的增大）而减少

由上可知：古诺竞争情形下，生产有差异化产品的两个企业进行研发创新时的研发投入、生产数量的均衡解、最优研发补贴可总结为表1所示。

表1 研发投入、利润、生产数量的均衡解以及最优研发补贴

三、产品差异性、技术溢出与研发时间关系分析

考虑到企业进行研发创新的时间以及创新成功的时间，本文下面将对生产有差异化产品的两竞争企业的研发创新投入进行分析。假设企业 ,i j开始对技术进行研发投入的时刻记为时间由于企业研发时间不同，下分别用1,2也代表企业 ,i j。企业1,2分别在时刻T12, T技术研发成功并成功投入生产产品，那么可得企业1,2的贴现利润总和为：

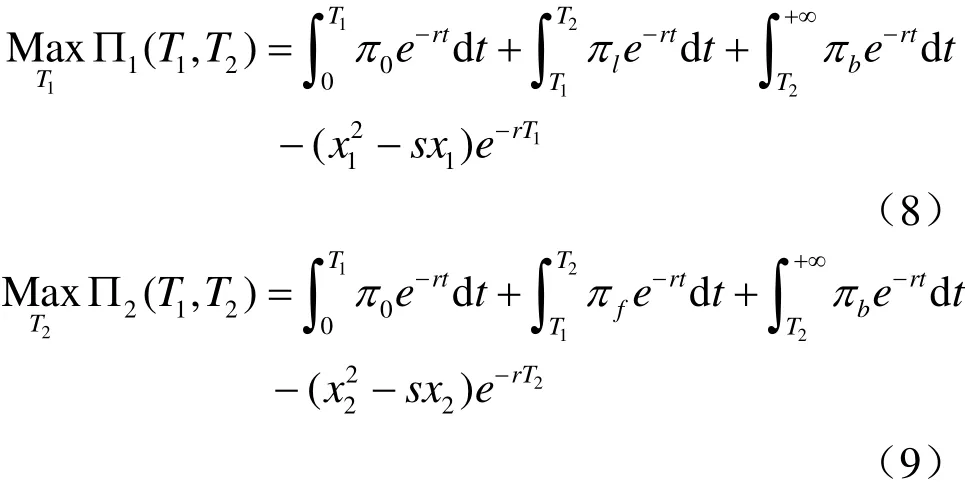
其中 π0表示两企业产品生产成本都为c时古诺均衡下的最大利润，表示企业1成本下降为企业2成本为c时的古诺均衡下企业1的最大利润，表示企业1成本下降为企业2成本下降为时古诺均衡下的最大利润，πf表示企业2成本为c，企业1成本下降为时古诺均衡下企业2的最大利润，对式（8），（9）求导可得：

由于企业在研发投入之后的收益是增加的，否则企业不会进行研发创新，故由此可知也就是说政府对企业每一单位研发产出的补贴s必须小于企业进行研发对产品边际成本下降所做的贡献。

结论4 在古诺竞争情形下，企业获得利益最大化时政府对企业的每一单位的研发补贴s要小于企业进行研发对产品边际成本下降所做的贡献xi，且

也就是说企业对产品研发所做的贡献不能少于政府对企业的研发补贴值，否则社会福利将为负值，政府也不会对企业进行补贴。时，故有这说明首先研发成功的领先企业所获得的利润的增加值要比后研发成功企业所获得的利润增加值要大。也就是说两个互相竞争的企业研发成功的时间很重要，先研发成功的企业具有产品上的优势性，利润增加的要大一些。

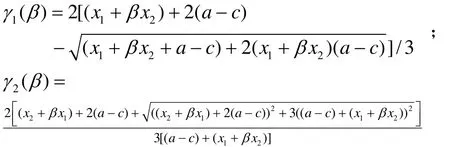
证明：由于企业研发成功的时间和利润的增加值呈反方向变化[13]，所以为了研究企业研发的时间与产品差异之间的关系，可先对企业利润的增加值进行计算分析，经过计算可得：

也就是说，若企业间产品差异较大，也就是γ较小时，企业间的研发竞争就会减弱，不易激发企业1的研发动力，使得企业对研发成功的时间不是很在意，企业的研发时间就要相对推迟一些，而导致T1增大；企业2研发成功时间晚一些，此时产品差异虽然较大，但随γ增大差异化在减弱，为了在竞争中减弱劣势驱使企业2尽快研发，将研发成功时间尽可能早些，从而T2变小。反之，若企业间产品差异较小，也就是γ较大时，企业间产品替代性非常强，竞争意识增强，会刺激企业研发的主动性，想尽快研发成功，越快越好，使得减小；而企业2研发成功时间晚一些，与企业1为竞争企业，不论产品差异大还是小，但随γ增大差异化在减弱，为了在竞争中减弱劣势，驱使企业2尽快研发，将研发成功时间尽可能早些，变小。

也就是说技术溢出越大，企业研发成功的时间就会越早。如果研发时间越大，技术溢出的就会越多，对本身企业就会不利，所以企业会想尽一切方法使得研发成功的时间尽可能早一些，避免技术溢出增大而带来的利益损失。对于企业2来说，如果溢出率较大，随着溢出的增加，与竞争企业相比，时间上不占优势，研发的压力增大，研发成功的时间会相对要提前，才能减少损失。对企业2来说，如果溢出率很小，又由于本身研发时间上处于劣势，已经可以从竞争对手中获得由于对手溢出而得的利益，这样不管溢出如何增大，溢出率都很小，企业2的研发成功时间相对来说要推迟。另外，由于在研发创新成功之后，企业才给予研发补贴，随着研发补贴的增多，竞争企业间为了尽早拿到多的研发补贴，只有让企业本身研发成功的时间减小，从而研发成功时间提前，还可以获得比竞争对手更多的竞争优势，取得更多的利润和研发补贴。

其中

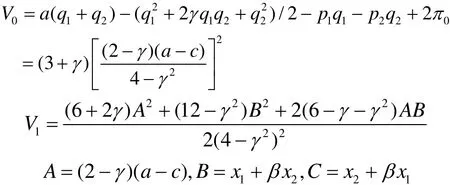
四、结束语

产品替代性的存在，使生产有差异化产品的企业间也存在竞争，尤其是替代性非常强时，企业间的竞争更激烈，促使企业对生产技术进行创新投资，以获得更大收益。同时，为了企业能给社会带来更多的社会福利，政府会采取各种政策激励企业不断进行创新，例如给予企业研发补贴、对有的企业减少征税等措施。本文对生产有差异化产品的两个竞争企业在创新研发过程中存在的技术溢出、研发补贴、产品差异、研发时间等因素进行了分析，并得出了古诺竞争情形下的各种均衡解和最优解，进一步分析了产品差异化、技术溢出、研发补贴对研发投入和研发时间的影响。分析研究表明，在存在技术溢出和政府研发补贴时，两个生产有差异化产品企业的研发投入随着研发补贴的增加，企业会增大研发投入。两个生产有差异化产品的企业在投资研发创新时，如果两企业的产品差异不大，并且政府给予企业的研发补贴不多时，技术溢出与两竞争企业的研发投入成反方向关系；如果企业的产品差异较大，并且政府给予企业的研发补贴较多时，技术溢出与企业创新投入呈正方向关系，此时技术溢出对企业创新投入有利。当企业之间的产品差异较小或者技术溢出不大时，或者当企业之间产品差异较大并且技术溢出较大时，存在最优研发补贴。在考虑研发时间的古诺竞争情形下，企业对产品研发所做的贡献不能少于政府对企业的研发补贴值，否则社会福利将为负值，政府也不会对企业进行补贴。产品差异较大或者较小时，企业研发时间随产品差异率的变化方向也不同。本文模型是考虑的同类型企业，对于不同类型企业如国有企业、部分私有化的国有企业、合资企业等企业的研发投入则需进一步分析。另外，政府的激励措施比较多，如减少税收、公共采购等鼓励企业研发的方式也可以考虑进去，也有待进一步探讨。

本文的结论可以为生产差异化产品的企业在制定研发投资策略时提供一些参考或者建议。企业之间产品差异化促使企业不断进行创新以获得市场优势，在创新研发投资过程中，如果产品差异较小且政府给予的研发补贴较少，技术溢出较大时，企业应该减少研发投入；如果技术溢出较小，企业应该增大研发投入。就研发企业的研发时间来讲，如果产品差异较大，企业间竞争就会减弱，后研发企业的研发时间要尽量提前；如果企业间产品差异较小，竞争会更加激烈，两企业都要采取研发时间提前策略，这样可减少企业在市场竞争中的劣势，以使企业利润达到最大。从政府的研发补贴策略来看，只要政府给予企业每单位的研发补贴小于企业研发之后产品边际成本下降值，社会福利就会比原来大。所以生产差异化产品的企业进行研发时，即使存在技术溢出，政府也应尽量采取给予企业研发补贴的鼓励措施。

[1] D’ASPREMONT C, JACQUEMIN A. Cooperative and noncooperative R&D in duopoly with spillovers[J]. American Economic Review,1988,78:1133-1137.

[2] HINLOOPEN J. Subsidizing cooperative and noncooperative R&D in duopoly with spillovers[J]. J Econ, 1997,66(2): 151-175.

[3] HINLOOPEN J. More on subsidizing cooperative and noncooperative R&D in duopoly with spillovers[J]. J Econ, 2000,72(3): 295-308.

[4] HINLOOPEN J. Subsidizing R&D cooperatives[J]. De Economist, 2001,149(3): 313-345.

[5] PIGA C, POYAGO-THEOTOKY J. Endogenous R&D spillovers and locational choice[J]. Regional Science and Urban Economics, 2005, 35: 127-139.

[6] TESORIERE A. Endogenous R&D symmetry in linear duopoly with one-way spillovers[J]. Journal of Economic Behavior & Organization, 2008, 66: 213-225.

[7] HINLOOPEN J, VANDEKERCKHOVE J. Dynamic efficiency of Cournot and Bertrand competition: input versus output spillovers[J]. J Econ, 2009, 98(2): 119-136.

[8] PETRAKIS E, POYAGO-THEOTOKY J.Subsidies versus R&D cooperation in a duopoly with spillovers and pollution[J]. Australian economic papers, 2002, 41(1): 37-52.

[9] SANDONís J, MARIEL P. Technology policy and antitrust in a polluting industry[J]. Prague Economic Papers, 2004(1): 67-81.

[10] FJELL K, HEYWOOD J S. Mixed oligopoly, subsidization and the order of firm’s moves: the relevance of privatization[J]. Economics Letters, 2004, 83: 411-416.

[11] JOSé GIL-MOLTó M, POYAGO-THEOTOKY J. R&D Subsidies, spillovers, and privatization in mixed markets[J]. Southern Economic Journal,2011,78(1): 233-255.

[12] SAHA B. Mixed ownership in a mixed duopoly with differentiated products[J]. J Econ, 2009, 98: 25-43.

[13] MILLIOU C, PETRAKIS E. Timing of technology adoption and product market competition[J]. International Journal of Industrial Organization,2011, 29: 513-523.

[14] PAL R. Technology adoption in a differentiated duopoly: Cournot versus Bertrand[J]. Research in Economics, 2010, 64: 128-136.

[15] 胡荣, 张骥骧. 技术溢出对双寡头R&D竞争演化的影响[J]. 系统管理学报, 2012, 21(5): 625-633.

[16] 生延超.创新投入补贴还是创新产品补贴: 技术联盟的政府策略选择[J].中国管理科学, 2008, 16(6): 184-192.

[17] 方海燕，达庆利. 基于差异产品的政府最优R&D补贴策略研究[J]. 中国管理科学, 2009, 17(3): 166-172.

[18] 马家喜, 仲伟俊, 梅姝娥. 不确定环境下基于Bertrand竞争的企业创新模式比较研究[J]. 管理工程学报, 2010, 24(1): 152-157.

[19] 韦铁, 鲁若愚. 技术外溢条件下企业自主创新投入问题研究[J]. 管理工程学报, 2011, 25(1): 83-87.

[20] 龙勇, 姜寿成. 基于知识创造和知识溢出的R&D联盟的动态模型[J]. 管理工程学报, 2012, 26(1): 35-41.

编辑 何 婧

Research of R&D Subsidies， Technological Spillovers and R&D Investment with Product Differentiation

ZHANG Wei ZHONG Wei-jun MEI Shu-e
(Southeast University Nanjing 211189 China)

Considering the government’s incentive policies to technological innovation, the technological spillovers of R&D process and product differentiation, this paper constructs a investment model of technological innovation for two competing firms producing differentiated products. First, we obtain equilibrium solution of the number of production, profits and R&D investment under Cournot competition without considering time. The optimal R&D subsidies under the maximization of social welfare and the conditions for the existence of optimal R&D subsidies are derived, and the relationships among R&D subsidies, technological spillovers, product differentiation and R&D investment are analyzed. The result shows that when the product differentiation is small and R&D subsidies are lower, there are negative correlation between the R&D investment and technology spillovers. When the product differentiation is larger and R&D subsidies are higher, there are positive correlations between the R&D investment and technology spillovers. Furthermore, taking account of the successful time of R&D firms are different, the paper also analyzes the impact of product differentiation, technological spillovers and R&D subsidies on R&D successful time considering the interest in the model, and derives the optimal conditions in the case of the maximization of social welfare.

technological spillovers; R&D subsidies; product differentiation; R&D investment; R&D time

F830.59; F11.0

A [DOI]10.14071/j.1008-8105(2015)05-0094-08

2014 - 01 - 11

国家科技部支撑计划项目（2012BAH29F01）；国家科技部创新方法工作专项项目（2013IM030600）；江苏省软科学研究计划项目（BR2014095）.

张伟（1982- ）男，东南大学经济管理学院博士研究生；仲伟俊（1962- ）男，东南大学经济管理学院教授，博士生导师；梅姝娥（1968- ）女，东南大学经济管理学院教授，博士生导师.