基于组合赋权VIKOR模型的电子政务项目评标方法研究
□谭世海 段 磊 黎 亮
[电子科技大学 成都 611731]
引言
在电子政务项目建设流程的采购招标阶段,评标工作是非常重要的环节,它直接影响着电子政务项目建设的最终成果。而能否公平、公正地选择最优的建设单位又取决于评标方法选取和制定的合理与否。
现阶段对电子政务项目建设阶段评标的研究文献较少,张艳辉和李宗伟从建设酬金、技术服务水平和资信状况等方面建立评价指标体系,运用AHP-综合评分法选择最优投标单位[1]等。与其他工程项目一样,电子政务项目建设单位的选择也是一个典型的多属性决策问题。目前用于多属性决策问题的评标方法主要有层次分析法(AHP)[1~2]、灰色关联法[3~4]、模糊综合评价法[5~7]、数据包络分析方法(DEA)[8]、TOPSIS法[9]等。这些方法可以用于电子政务项目建设阶段的评标中,但是通过对相关文献的研究发现,这些方法都有一些缺陷:层次分析法完全根据专家经验进行判断,特征值和特征向量的求解较复杂,而且结果需要进行一致性检验;灰色关联法也需要人为参与且计算复杂;模糊综合评价法运算模型较多,选择不当会丢失信息,也有较多的人为因素,而且在确定指标隶属函数时,易造成已经“白化”的指标模糊化;DEA法无法确定有效决策单元的优劣顺序;TOPSIS法在考虑方案时选择离正理想解最近离负理想解最远的方案,却未考虑这两个理想点之间的相关性;而且有些方法在确定指标权重时,或单纯采用主观赋权(如AHP法)使结果太主观,或仅采用客观赋权(如商权法)而未考虑决策者偏好,致使确定的权重不能真实反映指标属性和决策者偏好,进而影响评标的结果。
针对现有方法存在的缺陷,本文采用VIKOR算法,并提出改进层次分析法[10]和标准离差法[11~12]相集成的主客观组合赋权法来确定指标权重,构建了基于组合赋权VIKOR模型的电子政务项目评标方法,最后通过实例对该模型进行验证分析。本文对电子政务建设项目的评标流程如图1所示。

图1 电子政务项目评标流程图
一、基于组合赋权VIKOR模型的电子政务项目评标方法的构建
VIKOR是Opricovic&Tzeng1998年提出的一种折中的多属性决策方法,它得到离理想解最近的折中可行解,属于一种多属性决策中最佳化妥协解方法[13~15]。VIKOR采用了由Lp-metric发展而来的聚合函数,其中p为聚合函数的距离参数,1 根据电子政务项目的特点和《政府采购货物和服务招标投标管理办法》的规定,本文主要从投标报价、投标单位组织设计、投标单位业绩、技术及服务水平、网站核心支撑产品、资信状况、建设工期及质量保证体系八个方面来构建评价指标体系,如图2所示,根据综合评价结果对投标企业进行优劣排序,然后选择最优投标企业。 图2 电子政务建设项目评价指标体系 不同量纲、不同数量级的数据不能直接进行比较和计算,若直接使用可能会造成决策失误,为了消除这一影响,需要对原始数据进行无量纲化处理。VIKOR算法采用线性规范化的方法处理。 在项目评标过程中,指标权重合理与否将会对决策结果产生很大影响。因此,项目指标赋权既要考虑决策者或专家们的意愿和偏好,又要反映各指标之间的客观差异,这样才能得到合理可靠的目标权重。改进层次分析法通过最优传递矩阵将比较矩阵转化为一致性矩阵,不需要再进行一致性检验,能够充分反映决策者或专家们的主观意愿和偏好。标准离差法能够考虑评价指标中的原有信息,但不能反映决策者的意愿。本文将二者结合构成主客观组合赋权法对指标进行赋权,增加了权重的有效性,从而有助于评标结果的科学性。 1.改进层次分析法求指标主观权重 改进层次分析法通过算法的改进使其结果无需检验就满足一致性要求。文献[10]已经证明了该方法的可行性。设一项目有n个指标,即S1,S2,…..,Sn,其对应的权重分别为W1,W2,…..,Wn,且本文采用3标度法代替传统的9标度法来建立判断矩阵,即当甲、乙两指标做比较时,当甲比乙重要时,用2表示;当甲和乙同等重要时,用1表示;当甲没有乙重要时,用0表示。具体步骤如下[18]: (1)首先对各项目指标进行两两比较,并建立判断矩阵为B=(bij)nxn, (2)求出B的最优传递矩阵为C=(cij)nxn,其中 (3)将矩阵C转化为一致性矩阵为D=(dij)nxn,其中dij=exp(cij); (4)用方根法求D的特征向量W=(w1,w2,…,wn,)T,其中wi作为各指标的权重。 2.标准离差法求指标客观权重 标准离差法确定指标权重就是先计算指标的标准差,然后根据指标的标准差大小确定指标的权重大小。其原理是如果某个指标的标准差越小,就说明该指标的变异程度越小,提供的信息量就越小,在综合评价中所起的作用越小,则该指标的权重就应越小;反之权重则越大。利用标准离差法计算各指标的权重公式为[11] 其中,σi是第i个指标的标准差,wi为第i个指标的权重。 3.权重的组合 设wk为第k个指标的组合权重,w1i为由改进层次分析法确定的权重,为由标准离差法确定的指标权重,则指标的组合权重为 4.运用VIKOR模型确定最优投标单位 第一,根据以下公式确定各指标正、负理想解; 在式(5)和(6)中,i为各评价指标,j为各备选方案(投标单位),fij表示第j个投标单位的第i个评价值;I1为效益型准则集;I2为成本型准则集。 第二,根据以下公式计算各投标单位的群体效益sj、个别遗憾值Rj及其能产生的利益比率Qj; 在式(7)和(8)中,ωi表示第i个指标的权重;sj代表各投标单位的群体效益,其值越小,效益越大;Rj代表个别遗憾,其值越小,个别遗憾越小;在 式(9)中,s+=maxjsj;s-=minjsj;R+=maxjRj;R-=minjRj;v表示决策机制系数,且规定v=0.5。 第三,根据Qj、sj和Rj分别进行投标单位的优劣排序; 第四,当以下两个条件同时满足时,则选择Qj排序中最小的为最优投标单位。 条件一:Q2-Q1≥1/(J-1)。式中Q2表示根据Q排序出的第二个方案的值;Q1表示根据Q排序出的最优方案的值;J为投标单位的数目。当有多个方案时,需要依次比较排序第一、第二、第三、第四等方案之间是否满足条件一。 条件二:可接受的决策可靠度。 在Q排序中,排序第一方案的S值必须比第二的S小。或排序第一方案的R值比排序第二的R值小。当有多个方案时,需要依次比较排序第一、第二、第三、第四等方案之间是否满足条件二。 评判准则:若排序第一和第二的方案之间的关系同时满足条件一和二,则选择排序第一的方案;若第一和第二方案只满足条件二,则二者均为最优方案。 本文以成都市政府门户网站统一平台建设为例对VIKOR模型进行实证分析,该项目涉及相关硬件、网站管理辅助软件的购买和安装以及定制软件的开发工作等。项目建设采用招标的方式选择建设单位,共有四家合格的投标单位,根据调查研究得出各投标单位的评价指标值如表1所示。 表1 投标单位评价指标值 根据主、客观权重的计算步骤,以Matlab为工具求出指标的主、客观权重,并由式(4)求出组合权重;计算结果如表2所示。 表2 评价指标的主、客观及组合权重 1.该项目指标体系中,投标报价和建设工期为成本型指标,其它指标为效益型指标,根据式(5)和(6)确定指标的理想解和负理想解。 2.根据式(7)、(8)、(9)计算四家投标单位的S,R,Q值,如表3所示。 表3 四家投标单位的S、R、Q值 3.由表3得出四家投标单位的VIKOR排序,如表4所示。 表4 四家投标单位的VIKOR排序 4.根据判断法则,结合表3和表4,我们得出最终的优劣排序为B>A>C> D,最优投标单位为B。 本文将多属性决策中的VIKOR模型应用于电子政务项目建设的投标单位的选择过程,并根据对电子政务项目的特点和建设要求的分析,从投标报价、投标单位组织设计、投标单位业绩、技术及服务水平、网站核心支撑产品、资信状况、建设工期及质量保证体系八个方面建立评价指标体系,提出了改进层次分析法和标准离差法相集成的主客观组合赋权法,构建了基于组合赋权VIKOR模型的电子政务建设项目评标方法。该方法通过最大化群体效益和最小化个体损失,得到决策者接受的满意解,它综合考虑了定性指标和定量指标,实现了主观和客观的集成,减小了现有方法在权重确定和评标过程中的主观性,提高了评标决策的科学性,而且操作简单易于实现,具有一定的实用性。 [1]张艳辉,李宗伟.AHP-综合评分法在电子政务项目招标中的应用[J].工业技术经济,2007,26(3):89-92. [2]侯立中,吴俊霞.层次分析法在石油工程评标中的应用[J].技术经济,2006,25(5):113-115. [3]刘晴,王建平,王丛莹.基于灰色关联理论的建设工程评标方法研究[J].工程管理学报,2010,24(2):152 -155. [4]石振武,柳鹏.基于模糊数学和灰色关联的工程项目评标方法研究[J].森林工程,2006,22(1):55-57. [5]李志勇,王顺洪.基于模糊综合评判的工程评标方法[J].重庆建筑大学学报,2003,25(4):108-113. [6]吴耀兴,陈政辉.模糊综合评价法在工程项目评标中的运用[J].建筑经济,2009(10):64-67. [7]杨开云,冯卫,王亮,等.模糊层次分析法在建设工程评标中的应用[J].建筑经济,2006(12):143-146. [8]段永瑞,田澎,张卫平.基于DEA的供应商选择方法研究[J].工业工程与管理,2004(2):71-74. [9]苏春,董劲,张先起.基于信息熵的TOPSIS模型在水利工程评标中的应用[J].东北水利水电,2006(1):67-69. [10]马农乐,赵中极.基于层次分析法及其改进对确定权重系数的分析[J].水利科技与经济,2006,12(11):732-736. [11]王昆,宋海洲.三种客观权重赋权法的比较分析[J].技术经济与管理研,2003(6):48-49. [12]迟国泰,李刚,程砚秋.基于AHP-标准离差的人的全面发展评价模型及其实证研究[J].管理学报,2010,7(2):303-310. [13]OPRICOVIC S.Multicriteria optimization of civil engineering systems [J].Faculty of Civil Engineering,Belgrade,1998,2(1):5-21. [14]刘鸿雁,阎涛,王光远.基于AHP和VIKOR算法的评标方法研究[J].技术经济,2009,28(5):22-34. [15]OPRICOVIC S,TZENG G H.Multicriteria planning of post-earthquake sustainable reconstruction[J].Computer- Aided Civil and Infrastructure Engineering,2002,17(3):211-220. [16]OPRICOVIC S,TZENG G H.Compromise solution by MCDM methods:A comparative analysis of VIKOR and TOPSIS [J].European Journal of Operational Research,2004,156(2):445-455. [17]赵颖涛.基于VIKOR算法对供应链合作伙伴的优选[J].电力科学与工程,2010,26(4):45-48. [18]张丽霞,施国庆,丰景春.基于物元模型的索赔决策研究[J].河海大学学报,2006,34(1):108-111.(一)建立电子政务项目评价指标体系

(二)指标数据无量纲化处理
(三)评价指标的组合赋权


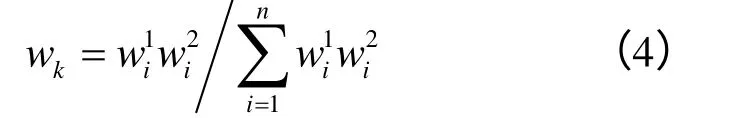


二、实证分析

(一)根据式(1)、(2)得无量纲化矩阵

(二)计算各指标主、客观和组合权重

(三)最优投标单位的确定



三、结论

