某扭杆式平衡机设计和疲劳仿真
刘威(中国船舶重工集团公司第七一〇研究所,湖北宜昌443003)
某扭杆式平衡机设计和疲劳仿真
刘威
(中国船舶重工集团公司第七一〇研究所,湖北宜昌443003)
依据某型火箭发射装置俯仰运动特性,设计了扭杆式平衡机,确定扭杆的材料和工艺要求。基于线性累积损伤Miner理论,通过ANSYS软件的疲劳分析工具计算,获得该扭杆累积寿命耗用系数,验证了扭杆设计正确性,解决了扭杆疲劳定量分析不足问题。
火箭发射装置;扭杆;ANSYS
0 引言
火箭发射装置总体设计时,为实现发射装置大仰角发射,同时为了降低火箭发射装置高度,需要将耳轴布置在俯仰部分质心的后方,这样俯仰部分的质量对耳轴产生了重力矩。为了克服重力矩,降低电机的功率,总体设计中需要配置平衡机[1]。平衡机的作用就是对俯仰部分提供一个推力或拉力,用于产生一个抵消绕耳轴的重力矩的平衡力矩。平衡机按储能元件分为弹簧式、扭杆式和气动式三种,扭杆式平衡机是利用扭力杆变形时产生的扭矩来平衡俯仰部分的重力力矩[2]。
本文以某型发射装置扭杆式平衡机为实例,设计了四连杆机构和扭杆,确定扭杆的材料和工艺要求。利用ANSYS软件的疲劳分析工具,计算得到了扭杆累积寿命耗用系数,解决了扭杆疲劳定量分析不足问题。
1 平衡机结构设计
1.1设计计算依据
某型发射装置采用扭杆式平衡机,发射角α的角度变化范围为0°~75°。发射装置俯仰角度在0°~40°范围运行时,俯仰体重心位于耳轴前部,俯仰角度在40°~75°范围运行时,俯仰体重心位于耳轴后部,对扭杆产生双向扭转力矩。由于发射装置在使用中存在空载、满载和非满载等多种状态,扭杆产生的扭力矩应综合考虑空载和满载两种极限状态的不平衡力矩。
(1)空载不平衡力矩
空载时的不平衡力矩主要是由俯仰体的自身重量直接产生的,按公式(1)计算数值:

式(1)中,M空载——空载时的不平衡力矩,N·m;
m俯仰体——俯仰体质量,m俯仰体=1 500 kg;
g——重力加速度,g=9.8m/s2;
R空载——俯仰体质心到耳轴的距离,R空载=0.563 9m;
α空载——俯仰体质心与耳轴的连线与机座平面的夹角,α满载=52.276 5°。
当发射角分别取α=0°,5°……,75°时,通过直接计算得到的。依据做图法,按比例绘制的空载时不平衡力矩曲线,见图1。
(2)满载不平衡力矩
满载时的不平衡力矩为:

式(2)中,M满载——满载时的不平衡力矩,N·m;
m弹药——俯仰体质量,m俯仰体=1 800 kg;
R满载——总质心到耳轴的距离,R满载=0.652 5m;
α满载——总质心与耳轴的连线与机座平面的夹角,α满载=50.160 7°。
当发射角分别取α=0°,5°……,75°时,通过直接计算得到的。依据做图法,按比例绘制的满载时不平衡力矩曲线,见图1。
由图1可知,当发射角α=0°,满载不平衡力矩最大M满载=13 518.6N·m,其空载力矩也达到最大M空载=5 071.8N·m。满载、空载的平均力矩为:

由图1可知,当发射角α=75°,满载不平衡力矩最大M满载=12 152N·m,其空载力矩也达到最大M空载=5 020.5N·m。满载、空载的平均力矩为:
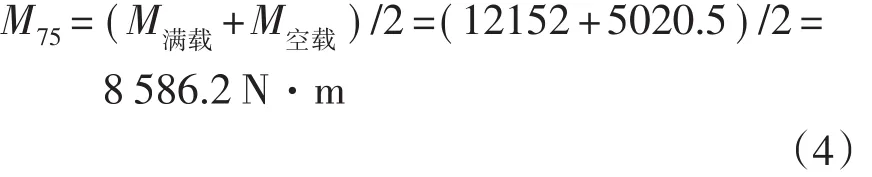
设计时以发射角α=0°时的平均最大不平衡力矩M最大平均作为设计计算的依据。

1.2四连杆机构设计
(1)结构设计
该发射装置采用两套单侧双扭杆式平衡机,前后布置,其中摇架体、BC杆、CD杆和固定基座形成了平衡机一的四连杆机构,摇架体、EF杆、FH杆和固定基座形成了平衡机二的四连杆机构。由于两平衡机均采用平行四边机构,满足了CD杆、FH杆跟随发射装置射角变化而引起扭杆受扭要求,并且CD杆、FH杆与摇架1∶1同步运动,将发射装置射角变化转化扭杆扭转角度变化,见图2。

图2 扭杆平衡机布置图
两扭杆采用实心圆柱扭杆结构形式,可选用45CrNiMoVA铬镍钼优质合金钢或60Si2MnA硅锰优质合金弹簧钢。45CrNiMoVA弹簧钢通过870℃油淬火,200℃低温回火,再喷丸、强扭,则具有很高力学性能。扭杆弹簧的脉动许用切应力约为:
(2)各杆长度参数
平衡机一,初选四杆机构各杆长度为:
a1=LAB=300mm,b1=LBC=400mm,
c1=LCD=300mm,d1=LDA=400mm。
平衡机二,初选四杆机构各杆长度为:
a2=LAB=400mm,b2=LBC=533.3mm,
c2=LCD=400mm,d2=LDA=533.3mm。
(3)最大预扭角和最大预扭力矩
平衡机一、平衡机二均采用四连杆机构采用平行四边形结构形式,发射装置俯仰范围为0°~ 75°,发射角为0°时,扭杆的最大预扭角。

由于平衡机一、平衡机二采用相同结构形式,最大预扭角相同,单杠平均不平衡力矩。
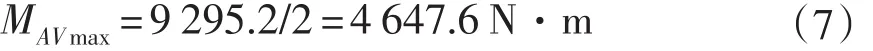
通过四杆传递给扭杆的最大预扭力矩。

1.3扭杆计算
(1)扭杆结构设计和计算
根据发射装置俯仰运动范围为0°~75°,扭杆至少提供±37.5°输出范围。由于发射装置总体尺寸限制,初选平衡机一和平衡机二的扭杠有效长度L1=L2=1 500mm,两端加工花键,见图3。

图3 扭杆三维图
(2)扭杆直径计算

取扭杆直径d=35mm
(3)扭杆切应力校核

式(10)中,τ——扭杆扭切应力,MPa;
[τ]——扭杆许用应力,MPa;
[τ-1]——脉动切应力作用下的许用扭切应力,MPa;
ks——对称扭切应力作用下的许用应力折算系数,一般取0.7;
[s]——扭杆的扭切应力许用安全悉数,取1.25。
故合格。
(4)花键校核
扭杆两端采用渐开线花键,初选模数为2,齿轮数:20。由静连接强度公式,可得

式(11)中,σp——花键挤压压力;
ψ——各齿间载荷不均匀系数,本文取0.75;
Z——花键得齿数,20;
l——齿的工作长度,取28mm;
h——健齿工作高度,h=m=2;
Dm——花键分度圆直径,Dm=D= m×Z=20×2=40。
1.4加工要求[3]
普通工艺强扭,仅适合用于扭杆单向扭转。由于本装置采用双向扭杆,强扭工艺会使扭杆表面及一定深度的工作应力超过屈服极限,但低于强度极限,从而产生稳定的塑性变形区,故不能采用单向强扭工艺。因本项目扭杆为高强度(>500 MPa)杆弹簧,故其主要加工工序与普通扭杆弹簧区分。
主要工艺流程:下料→外圆磨→钝头→平端面→车外圆→铣花键→抛光→淬火→回火→校直→预扭→探伤→抛丸→喷塑。
2 扭杆疲劳仿真
2.1疲劳分析[4]
强度、刚度和疲劳寿命是对工程结构和机械使用的三个基本要求。疲劳破坏是工程结构和机械失效的主要原因之一,引起疲劳失效的循环载荷的峰值往往远小于根据静态断裂分析估算出来的“安全”载荷。大多数工程结构或机械的失效是由一系列的变幅循环载荷所产生的疲劳损伤的累积而造成的。按照疲劳累积损伤规律,目前可以分为线性疲劳累积损伤理论、修正的线性疲劳累积损伤理论和非线性疲劳累积损伤理论。线性累积损伤理论中典型的是Palmgren-Miner理论,简称为Miner理论。
(1)一个循环造成的损伤:

式(12)中,D——疲劳损伤;
N——当前载荷水平的疲劳寿命。
等幅载荷下,n个循环造成的损伤:

变幅载荷下,n个循环造成的损伤:

临界疲劳损伤DCR:若是常幅循环载荷,显然当循环载荷的次数n等于其疲劳寿命N时,疲劳发生了,即n=N,由式(14)得到

该发射装置扭杆所受载荷具有循环载荷特征,符合Miner理论。
2.2仿真计算
ANSYS软件结构静力分析用来求解外载荷引起的位移、应力和力,ANSYS程序中的静力分析不仅可以进行线性刚强度分析,而且进行疲劳后处理分析。ANSYS疲劳计算依据美国机械工程师学会(ASME)给出了计算范围准则、简化的弹塑效应和Miner规则的积累疲劳求和法。该发射装置扭杆疲劳分析首先进行扭杆在静力条件下应力分析,然后采在后处理器POST1中进行疲劳计算[5]。
(1)在静力条件下应力分析
为了减少计算量,将模型进行简化:去掉两端花键特征,将模型转化为光杆。在Ansys中,对导入模型进行前处理工作。材料设置为Young’s Modlus弹性模量E=2.1×105 MPa,Poisson’s Ratio泊松比0.3。采用自动划分法(Automatic)方法自动设置扫掠网格划分,网格信息统计共有968个节点和315个单元,见图4。将扭杆一端固定,另一端施加扭力矩M1max=M2max=4 647.6N·m。应力结果见图5,可得最大应力为1 118MPa,最大应力点发生在节点351,小于该扭杠材料屈服极限1 550MPa,满足强度要求。

图4 扭杆网格划分图

图5 扭杆应力图
(2)材料S-N曲线
根据扭杆材料是45CrNiMoVA弹簧钢通过870℃油淬火等工艺获得,可以得到该种材料S-N曲线,列表见表1。
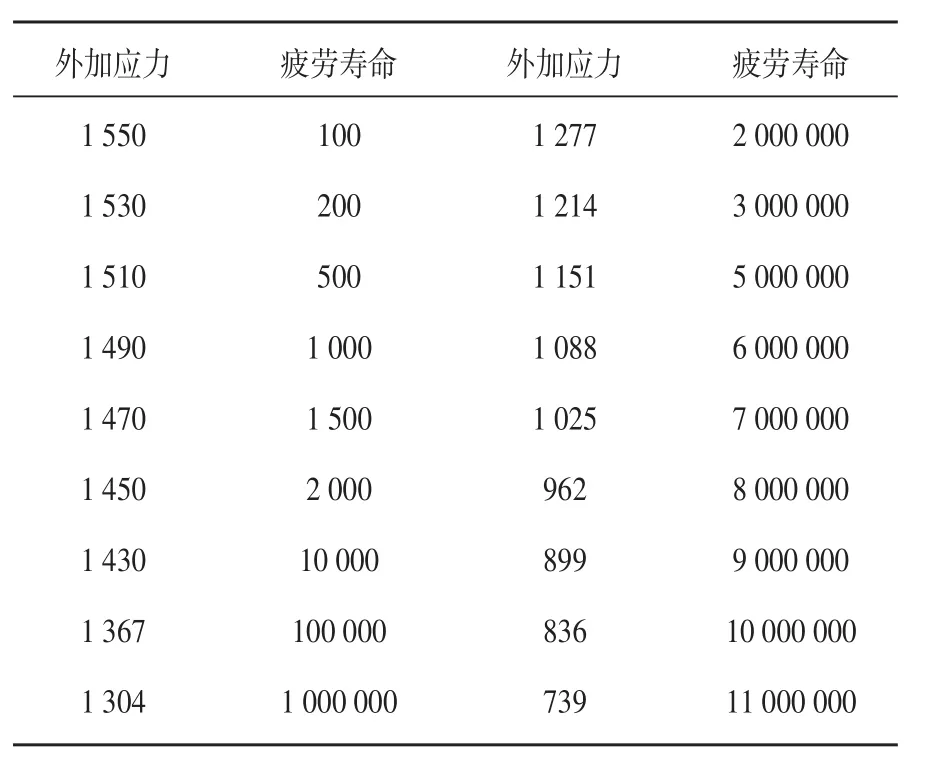
表1 S-N曲线表格
(3)疲劳计算
建立位置(Location)、事件(Event)和载荷(Loading)的数目,存储节点351的应力数值。指定事件重复次数N(15年更换周期)。

式(16)中,n天——表示1天循环次数,n天=100次。
激活疲劳计算,可得到节点351处的累积寿命耗用系数为0.232 87,满足了15年全日制工作时间内使用使用条件。
3 结论
(1)通过对扭杆的结构设计和校核,证明了采用扭杆式平衡机具有尺寸小,结构简单,同步性好的特点;
(2)基于线性累积损伤Miner理论,采用AN⁃SYS的疲劳计算工具,得到了在使用期限内扭杆累积寿命耗用系数,验证该扭杆设计满足使用条件,为定量计算扭杆疲劳寿命提供有效方法。
[1]李军,马大为,曹听荣,等.火箭发射系统设计[M].北京:国防工业出版社,2008.
[2]杨磊,方子帆.两级扭杆式平衡机设计及优化[J].机械研究与应用,2009,22(6):73-75.
[3]郭连忠,石明全.某发射装置串联式扭杆平衡机的设计[J].机械,2011,38(2):54-59.
[4]姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2003.
[5]陈晓霞.ANSYS 7.0高级分析[M].北京:机械工业出版社,2004.
(编辑:向飞)
Design and Fatigue Simulation of the Torsion Bar Balancer
LIUWei
(No.710R&DInstitute,CSIC,Yichang443003,China)
On the basis of the pitchingmotion characteristics of the rocket launcher,design the torsion bar balancer,determinematerial science and the process requirements of the torsion bar.Based on the linear cumulative damage Miner theory,through the calculation of fatigue analysis tool of ANSYS,get the cumulative lifetime consumption coefficientand verify that the design of the torsion bar is correct,solve the problem that thequantitativeanalysisof fatigue is lack.
rocket launcher;torsion bar;ANSYS
TH13
A
1009-9492(2015)04-0047-05
10.3969/j.issn.1009-9492.2015.04.013
2014-11-20
刘威,男,1979年生,辽宁盘锦人,硕士,高级工程师。研究领域:发射装置设计和控制工程。已发表论文9篇。

