工业机器人的鲁棒有限时间稳定性跟踪控制*

田雪虹（广东海洋大学寸金学院，广东湛江524094）

工业机器人的鲁棒有限时间稳定性跟踪控制*

田雪虹
（广东海洋大学寸金学院，广东湛江524094）

考虑工业机器人系统存在的参数未知、负载突变及外界干扰等各种不确定性，提出了一种有限时间稳定性的轨迹跟踪控制方法。该方法利用时延实时在线估计系统的各种不确定性和实际动力学特性，其估计误差由变结构项进行补偿，因而具有较强的鲁棒性和抗干扰性能，并且不需要机器人系统复杂的动力学模型知识。理论分析证明了机器人的闭环系统是有限时间稳定的，收敛速度快，跟踪精度高。通过对2自由度工业机器人的数值仿真说明了该算法的有效性。

工业机器人；时延估计；有限时间稳定；跟踪控制

0　引言

随着我国对产业结构调整和升级的迫切要求，工业机器人作为一种高度自动化的智能装备，在汽车制造业、机械加工业、电子制造业、食品加工业等各行各业获得广泛的应用，工业机器人必将逐步取代人工作业，这一趋势使得人们对工业机器人的性能要求越来越高，如智能化、模块化、高速、高精度等。由于工业机器人是一个高度复杂的、强非线性的多输入多输出系统，使得传统的独立伺服PID控制方法很难满足对高速高精度的性能要求，因此，研究先进的非线性控制技术如自适应控制、有限时间控制等方法具有重要的理论和现实意义。

有限时间稳定[1-2]是指系统的状态在有限的时间内到达平衡点，与渐近收敛的传统方法相比，瞬时特性更好，跟踪精度更高。因而，有限时间稳定性控制方法得到许多学者的广泛关注，并取得了一系统的研究成果，如文献[3-6]等。目前实现有限时间控制的常见方法有终端滑模控制方法，齐次理论方法，有限时间Lyapunov函数法等，其中终端滑模控制方法容易产生奇异[7]并且其不连续项会造成“抖振”，为此，文献[6]为避免奇异问题，提出了一种全局的非奇异终端滑模控制方法。为减少非奇异终端滑模控制的“抖振”问题，文献[8]提出了一种连续的终端滑模控制器，并成功应用于机器人系统的跟踪控制。文献[9]利用有限时间稳定性定理论，提出了一种基于PD和重力补偿策略的有限时间控制方法，保证了机器人系统跟踪误差的有限时间收敛。为获得更好的跟踪性能，文献[10]提出了基于非线性PD的全局有限时间稳定的控制器。接着文献[11]提出了基于修正机器人逆动力学的有限时间控制方法，从而保证了闭环系统的全局有限时间稳定。但以上这些方法都需要已知机器人的动力学模型，难以实际应用，而文献[12]将时延估计机器人的动力学模型，却无需机器人的动力学模型知识，但饱和函数的应用牺牲了跟踪精度。实际上，采用模糊小波神经网络也可以逼近机器人的未知动力学部分[13]，但大量的模糊规则使得算法的复杂性增加。而时延估计方法[14]通过在线实时估计各种不确定性，并加以补偿，从而对参数变化和外界干扰均能表现出较强的鲁棒性，并且算法比较简单，不需要被控对象的动力学知识。因而时延估计方法在许多机电系统领域获得广泛应用，如工业机器人[12，15-18]、DC伺服电机[19]等。

本文考虑工业机器人系统的各种不确定性，利用时延估计的鲁棒性特点，设计了一种鲁棒有限时间稳定的控制策略以提高机器人的跟踪精度。

1　有限时间稳定

首先介绍判别有限时间稳定性的有限时间Ly⁃apunov稳定性理论及相关概念。

定义1：有限时间控制：考虑非线性系统

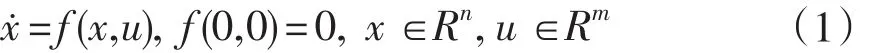
其中f:Rn×m→Rn是连续的。如果存在一个连续反馈控制律u=ϕ(x)，其中ϕ(0)=0，使得闭环系统的原点x=0是（局部）有限时间稳定的平衡点，则闭环系统=f(x,ϕ(x))是有限时间稳定的，此反馈控制律u=ϕ(x)被称为有限时间稳定性控制器。

引理1[1]：针对非线性系统（1），如果存在一个定义在原点邻域U⊂Rn上的函数V（x），并且V（x）是C1光滑的，且存在实数0<μ<1和c>0，使得下列条件成立：

（1）V（x）在U上是正定的；

则系统（1）是局部有时间稳定的。与初始状态x（0）=x0有关的停息时间为：

式（2）中x0为原点某一开邻域内的任意一点。如果U=Rn并且V（x）是正则的，则系统（1）是全局有限时间稳定的。

引理2[8]：对于任意给定的实数ai，i=1，…，n，若0<μ1<1，0<μ2<2，则以下不等式成立：

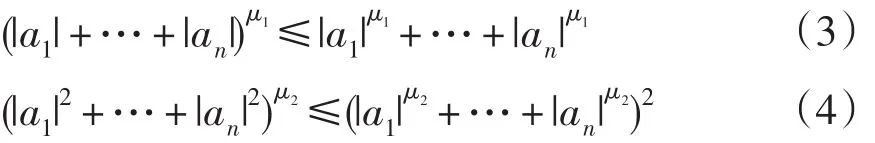
2　机器人的动力学模型

对于一个多输入多输出的n自由度关节机器人，其动力学方程可表示为

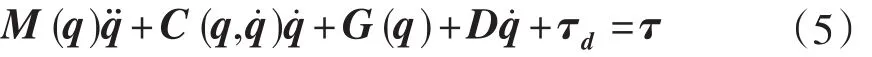
实际上，六自由度工业机器人的动力学方程是相当复杂的，由于各不确定性的存在，是很难甚至不可能获得机器人精确的动力学模型的。基于此，本文引入一个正定的常数矩阵，并令：

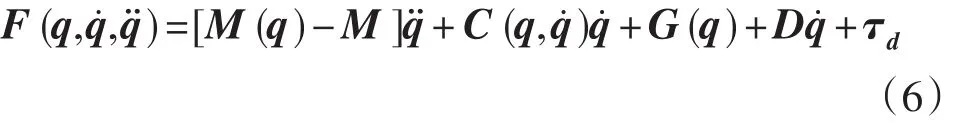
则机器人的动力学方程（5）可简化为

3　有限时间控制器设计及分析

工业机器人轨迹跟踪有限时间控制的目的就是使机器人的关节变量q能有效地跟踪期望的关节量qd，并且使跟踪误差e在有限时间内收敛至零，其中e(t),(t)∈Rn分别定义为e=q-qd,=-。

3.1有限时间控制

首先定义如下的Sig(·)α向量：

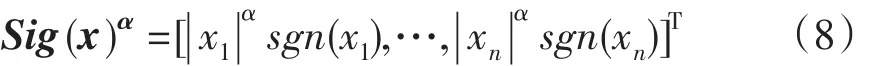
其中x=[x1,…,xn]T∈Rn，0<α<1，sgn(·)是标准的符号函数.

若令x1=e(t),x2==(t)，则具有不确定性的工业机器人系统（7）可表达为：

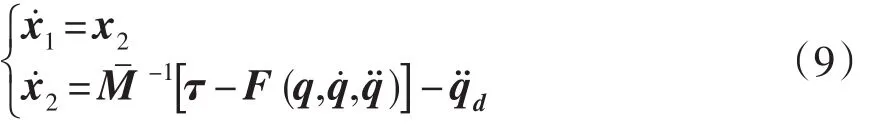
本文采用Backstepping技术，结合有限时间Lyapunov函数构造法来设计控制器，以实现机器人闭环系统的有限时间稳定。

第一步：引入辅助控制量φ(x1)∈Rn，且φ(0)=0，并定义如下误差变量：

则式（9）可表示为：

第二步：定义Lyapunov函数：

沿系统（9）的轨迹对V2求导并将式（11）代入得：

则沿系统（9）的轨迹有：

为实现系统跟踪误差的有限时间收敛，特设计如下辅助控制量以使式（13）满足引理1的条件（2）：

其中L1=diag(l11，l12，…，l1n)，l1i>0，i= 1，…，n。Sig(·)α的定义见式（8），并代入上式（13）可得：

如果z=0，则有：

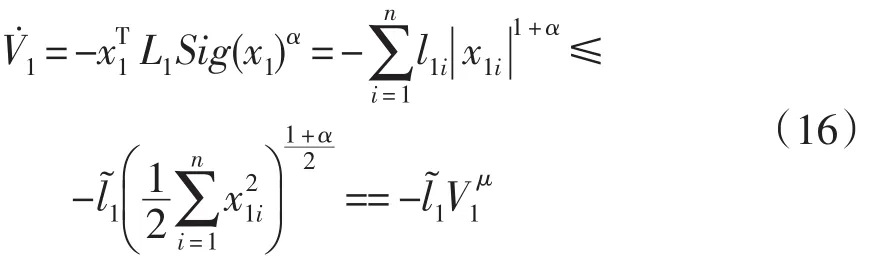
即系统是原点有限时间稳定的，其中l1min=min{l1i}，=2μl1min，μ=(1+α)/2，则1/2<μ<1。为此，需要进行下一步设计。

第三步：定义Lyapunov函数：

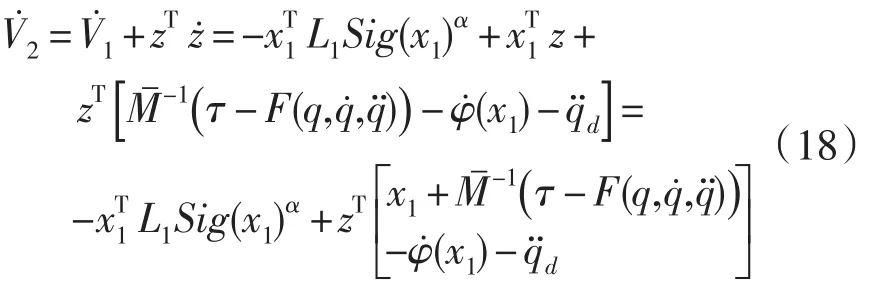
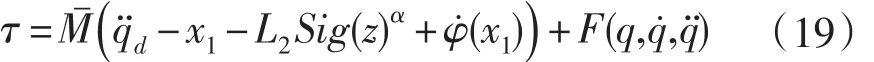
其中L2=diag（l21，l22，…，l2n），l2i>0，i= 1，…，n。将上式（19）代入式（18），由引理2可得：

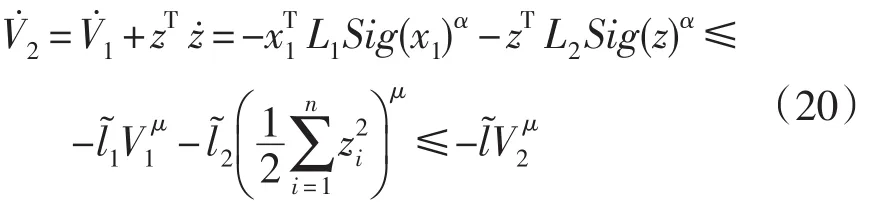
其中l2min=min{l2i}，=2μl2min，因此，根据引理1可知，机器人闭环系统是有限时间稳定的。但是控制器（19）是无法实际应用的，因为函数是未知的，为此，下面通过时延来估计并通过引入变结构项提高对时延估计误差的鲁棒性。

3.2时延估计

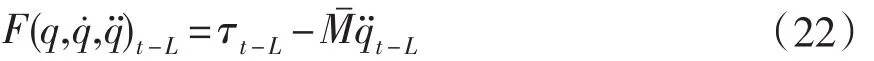
并通过变结构项来提高系统对估计误差的鲁棒性。

定理1：针对存在各种不确定性的机器人非线性系统（7），若设计如下控制器：

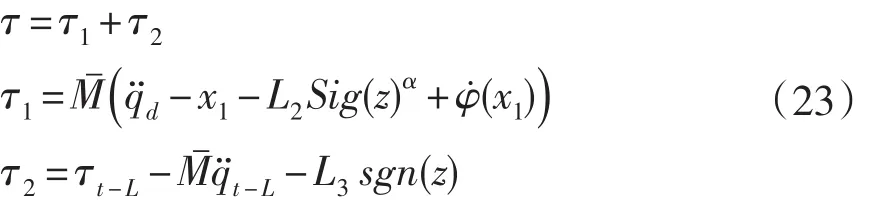
则该控制器作用下的机器人闭环系统是全局有限时间稳定的，其中L3=diag(l31，l32，…，l3n)，l3i>0，i=1，...，n。

显然，该控制器根据式（19）可实时估计出含有各种不确定性和实际动力学特性的实际应用时，t-L时刻的关节加速度可利用差分法计算得出，即：

下面证明闭环系统的全局有限时间稳定性。

证明：将控制律（23）代入（18）可得：

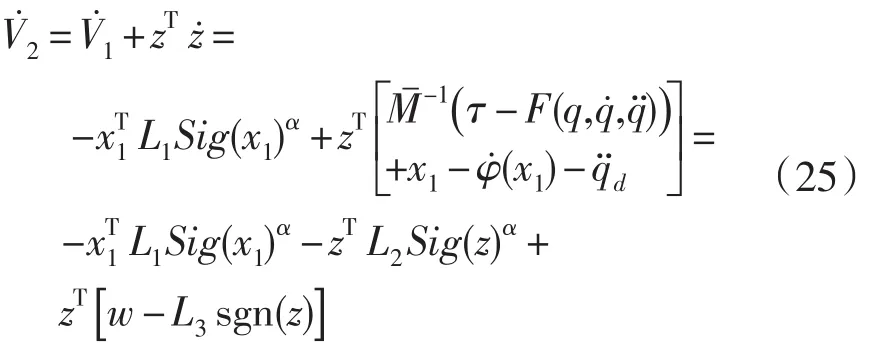
式中w为时延估计误差，即：

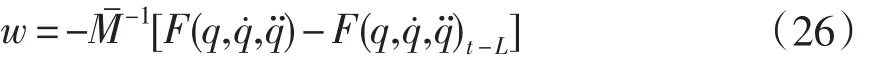
如果选择k3i≥ε，则有

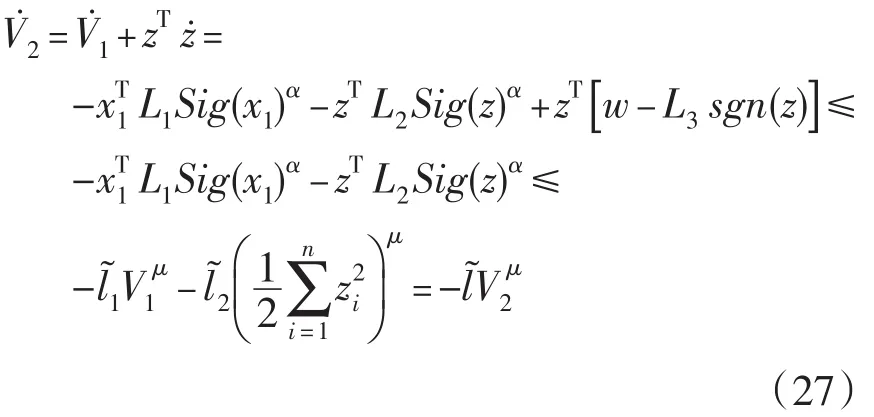
证明完毕，并且系统的调整时间为

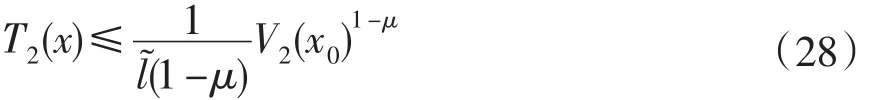
说明1：为避免变结构项K3sgn(z)产生的高频“抖振”影响控制性能，本文采用饱和函数法加以消除，但这不会影响系统的有限时间收敛特性。

其中δ为较小的正常数。

说明2：由于φ(x1)=-L1Sig(x1)α，当x1i=0且≠0时，(x1)无穷大，从而产生奇异，为此本文引入阈值λ>0来避免奇异，即：

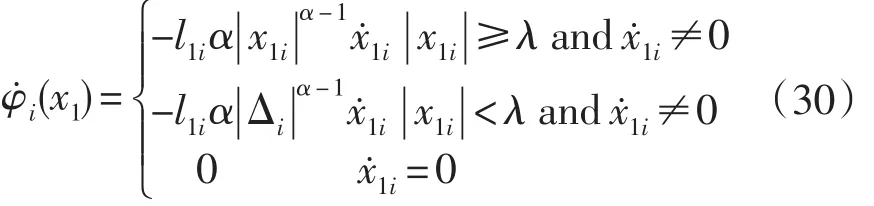
说明3：由于较小的α，可获得较快的误差收敛速度，但会增加系统的控制输入量，为避免输入饱和，建议选择0.7<α<0.9。

4　仿真

该部分通过对2自由度的工业机器人的数值仿真实验以说明本文方法的有效性和可行性，其动力学模型如下：

其中

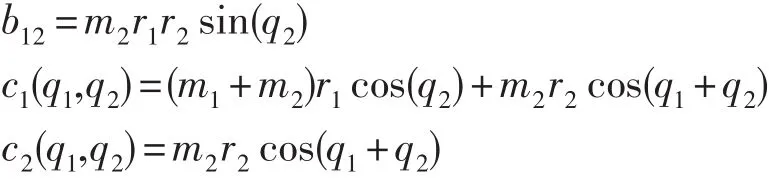
机器人动力学模型的参数r1=1m，r2=0.8m，J1=5 kg·m，J2=5 kg·m，m1=0.5 kg，m2=1.5 kg。机器人期望的跟踪轨迹为qd=[sin(2πt)，sin(2πt)]T，系统的初始条件为q(0)=[0.5，0.5]T，(0)=[0,0]T。控制器的相关参数设置如下:=diag(1,1)，K1=diag(10，10)，K2=diag(10，10)，K3=diag(10，10)，α=0.7，时延时间L=0.001 s，外界干扰设为τd=0.1+0.2q+0.5，在t=2~4 s时，出现突变干扰，设为τd2=2。

为说明本文算法的优点，与文献[11]提出的全局有限时间逆动力学方法(简记为FIDC)进行比较，其控制律为：

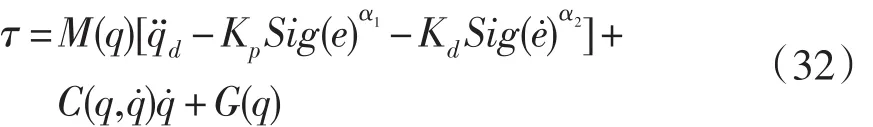
其中控制参数设置为：Kp=diag(50，50)，Kd= diag(50，50)，α1=0.5，α2=2α1/(α1+1)=2/3，并且该控制律（33)中均假设机器人的动力学模型完全已知。数值仿真结果见图1和图2，由图1可以看出，FIDC的收敛速度明显慢于本文方法，RFTC的跟踪误差小于FIDC方法。由于FIDC方法的动力学模型是完全已知的，因此说明本文方法具有较强的鲁棒性。控制输入量如图2所示，RFTC方法的控制量略有“抖振”，是由变结构项引起的，实际应用时用饱和函数代替。

图1　跟踪误差

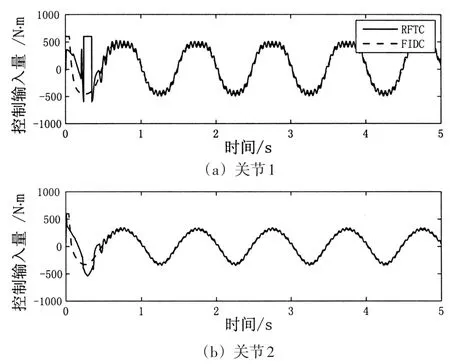
图2　控制输入量

总之，本文采用时延估计机器人的各类不确定性和动力学特性，使得算法结构更简单，更容易实现；并且有限时间稳定提高了系统的跟踪精度，改善了动态响应特性，非常适用于工业机器人高速高精度的轨迹跟踪控制。

5　结论

采用Backstepping方法设计了工业机器人有限时间稳定的控制器，一方面提高了响应速度，另一面确保了跟踪精度，变结构项的引入确保了系统具有较强的鲁棒性和抗干扰性能。采用时延在线估计机器人的各种不确定性和实际动力学特性，因而不需要机器人精确的复杂动力学知识。理论分析及仿真结果表明了本文方法的有效性和可行性。

［1］Bhat SP，Bernstein DS.Finite-time stability ofhomoge⁃neous systems［C］.Proceedings of the American Con⁃trolConference，1997：2513-2514.

［2］Haimo V T.Finite Time Controllers［J］.SIAM Journal on Controland Optimization，1986，24（4）：760-770.

［3］Bhat SP，Bernstein DS.Finite-time stability of continu⁃ous autonomous systems［J］.SIAM Journal on Control and Optimization，2000，38（3）：751-766.

［4］Hong Y，Wang J，Cheng D.Adaptive finite-time con⁃trol of nonlinear systems with parametric uncertainty［J］.Automatic Control，IEEE Transactions on，2006，51（5）：858-862.

［5］Tang Y.Terminal sliding mode control for rigid robots［J］.Automatica，1998，34（1）：51-56.

［6］Feng Y，Yu X，Man Z.Non-singular terminal sliding mode control of rigid manipulators［J］.Automatica，2002，38（12）：2159-2167.

［7］Wu Y，Yu X，Man Z.Terminal slidingmode control de⁃ sign for uncertain dynamic systems［J］.Systems&Con⁃trol Letters，1998，34（5）：281-287.

［8］Yu S，Yu X，Shirinzadeh B，et al.Continuous fi⁃nite-time control for robotic manipulators with terminal sliding mode［J］.Automatica，2005，41（11）：1957-1964.

［9］Hong Y，Xu Y，Huang J.Finite-time control for robot manipulators［J］.Systems&Control Letters，2002，46（4）：243-253.

［10］Su Y.Global continuous finite-time tracking of robotma⁃nipulators［J］.International Journal of Robust and NonlinearControl，2009，19（17）：1871-1885.

［11］Su Y，Zheng C.Global finite-time inverse tracking con⁃trol of robotmanipulators［J］.Robotics and Comput⁃er-Integrated Manufacturing，2011，27（3）：550-557.

［12］Maolin J，Jinoh L，Pyung Hun C，etal.Practical Non⁃singular Terminal Sliding-Mode Controlof RobotManip⁃ulators for High-Accuracy Tracking Control［J］. IEEE Transactions on Industrial Electronics，2009，56（9）：3593-3601.

［13］Chuan-Kai L.Nonsingular Terminal Sliding Mode Con⁃trol of Robot Manipulators Using Fuzzy Wavelet Net⁃works［J］.Fuzzy Systems，IEEE Transactions on，2006，14（6）：849-859.

［14］Youcef-Toumi K，Wu S T.Input/Output Linearization Using Time Delay Control［J］.JournalofDynamic Sys⁃tems，Measurement，and Control，1992，114（1）：10-19.

［15］Hsia TC，Gao L S.Robotmanipulator control using de⁃centralized linear time-invariant time-delayed joint con⁃trollers［C］.Proceedings of the Roboticsand Automa⁃tion，IEEE International Conference on，1990：2070-2075 vol.2073.

［16］Han D，Chang P-h.Robust tracking of robotmanipula⁃tor with nonlinear friction using time delay control with gradient estimator［J］.Journal of Mechanical Science and Technology，2010，24（8）：1743-1752.

［17］刘海涛，张铁.基于时延估计和鲁棒h_∞控制的工业机器人跟踪控制［J］.华南理工大学学报：自然科学版，2012，40（01）：77-81.

［18］刘海涛，张铁.基于时延估计的机器人有限时间跟踪控制［J］.机床与液压，2012，40（23）：12-16.

［19］Park JH，Kim Y M.Time-Delay Sliding Mode Control for a Servo［J］.Journal of Dynamic Systems，Mea⁃surement，and Control，1999，121（1）：143-148.

(编辑：阮毅)

Robust Finite-Time Stability Tracking Control for IndustrialRobots

TIAN Xue-hong
（Cunjin College，GuangdongOcean University，Zhanjiang524088，China）

Consider various uncertainties of complex industrial robots，such as parameters uncertainties，load mutation and external disturbances，this paper presents a trajectory tracking controlmethod based on finite-time stability theorem.In thismethod，the various uncertainties and actual dynamics are online obtained by the time-delay estimation，the estimation error is compensated by variable structure terms，which has strong robustness.Thus，the proposed method doesn’t require knowledge of the complex dynamicmode of the robot system.The finite-time stability of robot loop system is proved by finite-time stability theorem，fast convergence and high-accuracy are provided.Simulationson a2-DOF industrial robotdemonstrate theeffectivenessof thisalgorithm.

industrial robot；time-delayed estimation；finite-time stability；tracking control

TP24

A

1009－9492(2015)04－0001－05

10.3969/j.issn.1009-9492.2015.04.001

*湛江市科技计划项目（编号：2012C3106006）

2014－10－11

田雪虹，女，1980年生，山东菏泽人，大学本科。研究领域：机器人技术及其工程应用。