冷却气膜与热障涂层交界处流场分析
李佳莉, 王玉璋, 王 星
(上海交通大学燃气轮机研究院,上海 200240)
随着航空发动机及地面燃机的迅速发展,涡轮高温叶片入口温度不断提高。目前国外新型军用燃气涡轮发动机的燃气温度已达1538~1871℃,而现役发动机的高温部件材料许用温度均在1100℃以下[1,2]。在目前先进燃气涡轮发动机中,高温热防护涂层以及高效冷却是涡轮叶片防护两大关键技术。先进的热障涂层能够在工作环境下降低热端部件温度170℃左右[3]。
热障涂层目前主要的制备工艺是电子束物理气相沉淀法(EB-PVD)和等离子喷涂(APS),这两种方法制备的热障涂层都是各向异性的非致密多孔状介质,其孔隙率在5% ~20%之间[4,5]。热喷涂涂层呈层状结构,表面比较粗糙;而物理气相沉淀涂层呈柱状结构,表面较为光滑,但其孔隙率较高且垂直于涂层基体表面;不同的制备工艺以及长时间服役导致的涂层微孔和微裂纹的变化,会对叶片表面高温燃气与冷却气膜流场产生不同的影响。
目前对叶片表面流固耦合流场的研究主要是采用传统的数值模拟从宏观上求解控制方程,探索冷气射流和高温衡流相互掺混的漩涡结构和流场分布形成及发展的影响因素如气膜孔孔型、孔几何参数和气动参数等[6~8]。高温燃气及冷却射流会直接冲击在涂层表面,而涂层微孔结构尺度大约为10 μm[9],目前从微观角度揭示热障涂层微结构对叶片表面流动特性影响的文献相对较少。
格子Boltzmann方法(LBM)是20世纪80年代基于分子动理论发展起来的一种新型的数值模拟,LBM从介观层面上考虑粒子团的迁移和碰撞,通过粒子分布函数演化来得到宏观问题的解,在研究具有复杂表面结构如多孔介质内流体流动与换热及渗流现象中得到了广泛的应用[10~13]。本工作基于不同热障涂层的微结构,研究冷却气膜和热障涂层交界处微观流动,分析不同涂层微结构对冷却气膜稳定性的影响。
1 数学模型
1.1 D2Q9格子Boltzmann方法
本工作采用Boltzmann-BGK碰撞松弛模型中的格子波尔兹曼模型的二维九速度(D2Q9)不可压格子Boltzmann模型[14],该模型可用来计算微观尺度下多孔材料、具有复杂表面结构的流固耦合流场分布;该模型的离散速度模型(图1)和速度配置(式(1))如下:

图1 D2Q9模型Fig.1 D2Q9 model
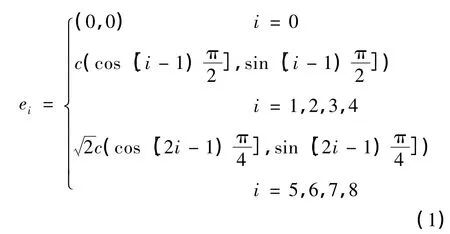
在无相变多孔结构内部及表面流场中,密度分布函数的演化方程为:

式中:r是坐标矢量,t是时间,τf是流体无量纲松弛时间;fi(r,t)和feqi(r,t)分别为与i方向相对应的粒子密度分布函数和平衡态密度分布函数。平衡态分布函数feqi(r,t)和无量纲松弛时间分别为:

其中ωf为密度分布函数的权系数,u为流体宏观流动速度,δt和δx分别为格子单位下对应的时间步长和网格步长,cs为格子声速,ν为流体黏性系数。
流体宏观密度和速率可由下式确定:
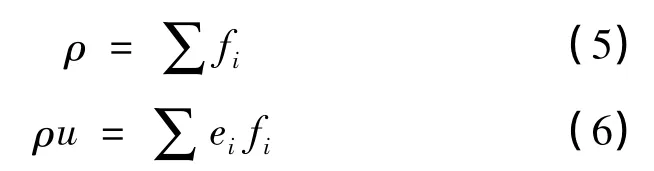
式中,u为流体宏观流动速度,ei为上文中图1所示二维九速度模型中不同方向的速度。
1.2 边界条件
真实结构热障涂层是多孔状介质,四参数随机生长方法在获取涂层几何结构模型上取得了较好的结果[15~17],本工作模拟热障涂层表面结构与冷却气膜耦合作用下的流场,以电镜扫描获得的柱状以及层状热障涂层真实结构为基础,如图2,3所示,其中黑色部分代表涂层固体材料骨架,灰白色区域为涂层孔隙及流体流动区域,经过灰度处理及Matlab像素识别功能,获得了0,1数值结构网格,局部网格结构如图2,3所示,经像素识别,图2中像素点为711×357,网格数为 NX×NY=711×357,其中涂层厚度约为78μm,每一格厚度为0.42μm;图3中像素点为716×281,网格数为NX×NY=716×281,其中涂层厚度约为 277μm,每一格厚度为 1.964μm,边界条件设置如图中所示:

图2 柱状结构涂层边界设置及网格结构Fig.2 Boundary condition and grid of columnar TBC

图3 APS喷涂结构涂层边界设置及网格结构Fig.3 Boundary condition and grid of TBC made by APS
1.2.1 左右边界条件
本工作模拟的流动区域为局部小范围区域,在稳态流动过程中,流体的流速和密度等宏观参数在左右边界变化很小,故在模拟中将流动区域的左右边界条件设置为周期性边界条件,同时忽略重力对流场的影响,如图4所示,以进口边界为例,进口边界节点未知分布函数f1,f5,f8,可由出口处相应节点粒子分布函数迁移得到,处理格式如下:

1.2.2 上边界条件
上边界为流体流动边界,模拟中给定上边界水平方向流动速度为U,竖直方向速度无脉动;密度采用与其相邻的内推节点的密度值,即:


图4 周期性边界条件示意图Fig.4 Periodic boundary condition

上边界的分布函数采用Guo等[18]提出的非平衡外推格式:

1.2.3 下边界条件
下边界为固体边界条件,该固体边界为无滑移边界,由真实结构知,在固体边界上无流体分布,对于固体边界有:

1.2.4 不规则固体骨架边界
反弹格式[19]常用于静止固体边界以及内部与流体接触的不规则固体骨架边界上,常用的处理方法就是对边界上的粒子作弹回处理,如图5所示边界节点(i,1),采用标准反弹格式来处理,即:

图5 标准反弹格式Fig.5 Bounce-back scheme

2 结果分析与讨论
基于上述模型,在Microsoft Visual Studio 2010平台上开发了微观尺度下流场分析软件,实现了对多孔涂层表面及内部气膜流动的数值模拟,其收敛条件设置为:


此处取ε为小量即ε=10-6,当两个相邻时层速度相对误差小于设定值ε即error≤ε时,计算收敛。
基于两种工艺制备的涂层微结构形成的计算网格,模拟流动参数如下:涂层表面掺冷气体温度Tf=1212℃,涂层底面温度Tc=844℃,上边界流体水平方向速度设为U=0.02(换算为实际流动速度约为23m/s),竖直方向速度无脉动;模拟中时间步长δt=1,格子步长δx=δy=1,图2所示模型流动无量纲松弛时间取为τf=0.602,图3所示模型流动无量纲松弛时间取为τf=0.523,流动计算中均选取格子单位下的无量纲量。
图6为不同涂层结构水平方向速度分布。由图可见,柱状结构涂层表面水平方向速度变化平稳,这是由于柱状结构表面较为平整;而层状结构涂层表面水平方向速度出现局部波动,这是由于层状结构表面比较粗糙。图7为不同涂层结构竖直方向速度分布,由图可见,柱状结构涂层孔隙中存在微弱的气体流动,降低了涂层的隔热性能,这是由于柱状结构涂层内部孔隙垂直于涂层表面,且孔隙往往与外部流场相通,孔隙率较高;层状结构涂层竖直方向速度波动幅度较大,气膜稳定性较差,对表面流场的黏性底层会产生较强影响。

图6 不同涂层结构水平方向速度分布(a)柱状结构;(b)APS喷涂层结构Fig.6 Horizontal velocity distribution of different coatings(a)columnar structure;(b)layered structure by APS

图7 不同结构竖直方向速度分布图Fig.7 Vertical velocity distribution of different coatings
图8中a和b分别为柱状结构涂层和APS喷涂层状结构涂层表面的气膜系统流线图及局部放大图。从放大图中可以清晰地看到流体在涂层表面的微孔间隙中产生了漩涡,紧贴涂层表面处流线明显波动,对流动产生了扰动。
图9中a和b分别为柱状和层状结构不同横截面竖直方向速度波动图,选取的三个截面分别从涂层表面至远流场边界,图中纵坐标取为流体竖直方向速度V与来流速度U的无量纲比。由图可见两种结构涂层在靠近表面处速度波动强烈,远流场区域速度波动趋于平缓,说明涂层表面微结构改变了流场流动状况。对于涂层表面处竖直方向上的速度波动,层状结构的波动幅度明显强于柱状结构,最大可达2.5%。涂层表面流体温度场与流场相互耦合,进而会影响流体温度场的分布。

图8 系统流线图及局部流线图 (a)柱状结构;(b)APS喷涂层状结构Fig.8 System flow diagram and local streamlines (a)columnar structure;(b)layered structure by APS

图9 不同横截面竖直方向速度波动图 (a)柱状结构;(b)APS喷涂层状结构Fig.9 Distribution of vertical velocity at different vertical sections (a)columnar structure;(b)layered structure by APS
3 结论
(1)采用LBM方法研究涂层微结构对气膜流动的影响,能够较好的反映真实的微观流场分布;
(2)热障涂层微结构对冷却气膜流动产生较大影响,涂层表面凹陷处产生漩涡,柱状结构涂层内部竖直孔隙中存在微弱的气体流动,降低了涂层的隔热性能;
(3)由于制备工艺不同,层状结构涂层表面比较粗糙,相比柱状结构对表面气膜流动的影响更加剧烈,竖直方向速度波动幅度可达2.5%(与来流速度无量纲比),气膜稳定性差;但在远流场区域两种结构涂层速度波动趋于平缓。
[1]文生琼,何爱杰,王皓.热障涂层在航空发动机涡轮叶片上的应用[J].燃气涡轮试验与研究,2009,22(1):59-62.(WEN S Q,HE A J,WANG H.Development of TBCs on turbine blade of aero-engine[J].Gas Turbine Experiment and Research,2009,22(1):59 -62.)
[2]李振军,张红松,魏媛.(La0.75Sm0.25)2Zr2O7陶瓷的热导率[J].人工晶体学报,2009,38(1):117-121.(LI Z J,ZHANG H S,WEI Y.Thermal conductivity of(La0.75Sm0.25)2Zr2O7ceramic[J].Journal of Synthetic Crystals,2009,38(1):117 -121.)
[3]GUO H B,VAEN R,STVER D.Atmospheric plasma sprayed thick thermal barrier coatings with high segmentation crack density[J].Surface and Coatings Technology,2004,186(3):353-363.
[4]魏绍斌,陆峰,何利民,等.热障涂层制备技术及陶瓷层材料的研究进展[J].热喷涂技术,2013,5(1):31-37.(WEI S B,LU F,HE L M,et al.Progress in processing techniques and ceramic materials of thermal barrier coatings[J].Thermal Spray Technology,2013,5(1):31 -37.)
[5]SCHULZ U,LEYENS C,FRITSCHER K,et al.Some recent trends in research and technology of advanced thermal barrier coatings[J].Aerospace Science and Technology,2003,7(1):73-80.
[6]郭婷婷,金建国,李少华,等.不同出射角度对气膜冷却流场的影响[J].中国电机工程学报,2006,26(16):117-121.(GUO T T,JIN J G,LI S H,et al.A numerical simulation in film cooling flows with different injection angles[J].Proceedings of the CSEE,2006,26(16):117-121.)
[7]WALTERS D K,LEYLEK J H.A detailed analysis of filmcooling physics:Part I—streamwise injection with cylindrical holes[C]//ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition.USA:American Society of Mechanical Engineers,1997:V003T09A052-V003T09A052.
[8]BOHN D,REN J,KUSTERER K.Conjugate heat transfer analysis for film cooling configurations with different hole geometries[C]//ASME Turbo Expo 2003,collocated with the 2003 InternationalJointPowerGeneration Conference.USA:American Society of Mechanical Engineers,2003:247-256.
[9]张红松,刘振启,关绍康.等离子喷涂纳米与微米 YSZ热障涂层的孔隙结构比较[J].表面技术,2010,39(5):4-7.(ZHANG H S,LIU Z Q,GUAN S K.Comparison of pore structure between plasma-sprayed nano-YSZ and micron-YSZ thermal barrier coatings[J].Surface Technology,2010,39(5):4 -7.)
[10]申林方,王志良,李邵军.基于格子 Boltzmann方法的饱和土体细观渗流场[J].排灌机械工程学报,2014,32(10):883-887.(SHEN L F,WANG Z L,LI S J.Mesoscopic seepage field of saturated soil with Lattice Boltzmann method[J].Journal of Drainage and Irrigation Machinery Engineering,2014,32(10):883 -887.)
[11]郭照立,郑楚光.格子Boltzmann方法的原理及应用[M],北京:科学出版社,2008:8.
[12]MADADI M,SAHIMI M.Lattice Boltzmann simulation of fluid flow in fracture networks with rough,self-affine surfaces[J].Physical Review(E),2003,67(2):026309.
[13]WANG J,WANG M,LI Z.A lattice Boltzmann algorithm for fluid-solid conjugate heat transfer[J].International Journal of Thermal Sciences,2007,46(3):228-234.
[14]何雅玲,王勇,李庆.格子Boltzmann方法的理论及应用[M],北京:科学出版社,2008:31-56.
[15]凌锡祥,王玉璋,王星,等.层状热障涂层孔隙微结构对其隔热性能影响的数值研究[J].中国有色金属学报,2015,25(2):408-414.(LING X X,WANG Y Z,WANG X,et al.Numerical study of effect of pore microstructure of layered thermal barrier coatings on thermal insulation performance[J].The Chinese Journal of Nonferrous Metals,2015,25(2):408-414.)
[16]凌锡祥,王玉璋,王星.基于柱状结构的热障涂层隔热性能数值研究[J].航空材料学报,2014,34(5):69-74.(LING X X,WANG Y Z,WANG X.Numerical study of thermal insulation properties of thermal barrier coating based on columnar structure[J].Journal of Aeronautical Materials,2014,34(5):69 -74.)
[17]WANG Y Z,WANG X,WENG Y W.Analysis of effective thermal conductivity of thermal barrier coatings based on microstructure[C]//ASME Turbo Expo 2014:Turbine Technical Conference and Exposition.USA:American Society of Mechanical Engineers,2014: V006T22A015-V006T22A015.
[18]GUO Z L,ZHENG C G,SHI B C.Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method[J].Chinese Phys-ics,2002,11(4):0366 -0374.
[19]ZIEGLER D P.Boundary conditions for lattice Boltzmann simulations[J].Journal of Statistical Physics,1993,71(5/6):1171-1177.

