空地微型导弹制导精度仿真分析
李志坚,刘晓利,刘名玥,陈志华
(1.南京理工大学瞬态物理国家重点实验室,南京 210094;2.中国人民解放军75756部队,广东 汕尾 516600)
近年来,随着无人机军事应用范围的不断拓展,为小型无人机执行侦察/打击一体化军事任务而研制装备的微型制导弹药已成为国内外高度关注的热点,例如美国的长钉(Spike)导弹、Archer无人机载微型导弹和Griffin多平台微型导弹等。这些微型导弹的特点是口径和体积小、质量轻,毁伤半径小、制导精度高,结构简单、成本低;可对敌近距离重要目标或低速机动目标实施精确打击。
导弹的制导精度受很多因素影响,有外界环境引起的,也有武器系统内在误差因素产生的。因此,制导精度分析是导弹研制过程中必须考虑的关键因素之一。国内外学者和工程技术人员在导弹制导精度分析和计算机模拟打靶方面已进行了很多研究,取得了丰硕的成果[1-4]。前人所采用的分析方法有蒙特卡洛(Monte-Carlo)法、协方差分析描述函数技术(CADET)和统计线性化伴随法(SLAM)等;研究的对象包含微型导弹、空空导弹、空地导弹和地地导弹等。但是,他们的研究和分析均没有考虑武器平台本身误差所造成的影响。
本文以某非旋转空地微型导弹为对象,采用蒙特卡洛方法进行了制导精度误差分析研究。通过大量仿真试验,归纳出包括武器平台误差在内的各误差因素的最大范围和模型处理方法。攻击固定目标时,采用如《GJB6289-2008地地弹道式导弹命中精度评定方法》中包含系统误差的CEP定义来描述导弹的制导精度;攻击运动目标时,则用脱靶量来描述导弹的制导精度。
1 仿真系统构建
用蒙特卡洛方法进行导弹制导精度分析,首先要建立导弹制导系统的数学模型,然后通过在计算机中编制计算程序,建立相应的程序模块构成制导系统的仿真软件。图1给出了导弹制导回路数字仿真的原理框图。
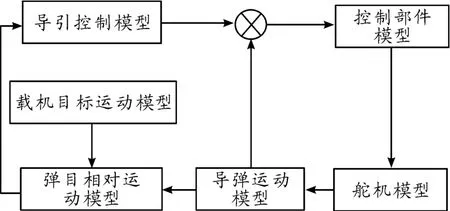
图1 导弹制导回路数字仿真原理框图
1)载机运动模型:本文建立的是载机平飞运动模型。
2)目标机动模型:描述目标的各种机动方式;一般分为固定目标和地面机动目标2类。
3)导弹运动模型:描述六自由度刚体的弹道模型,由动力学方程、运动学方程、质量变化方程、几何关系方程和控制方程等组成,见文献[5-6],不再赘述。
4)相对运动模型:描述导弹与目标之间的相对运动关系,见文献[5]。
5)导引控制模型:导弹采用比例导引法,导引律方程为
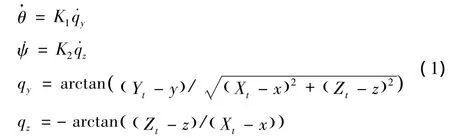
式中:θ为弹道倾角;ψ为偏航角;qy为视线高低角;qz为视线方位角;K1,K2为比例系数。
6)控制部件和舵机模型:其Simulink仿真框图如图2所示。
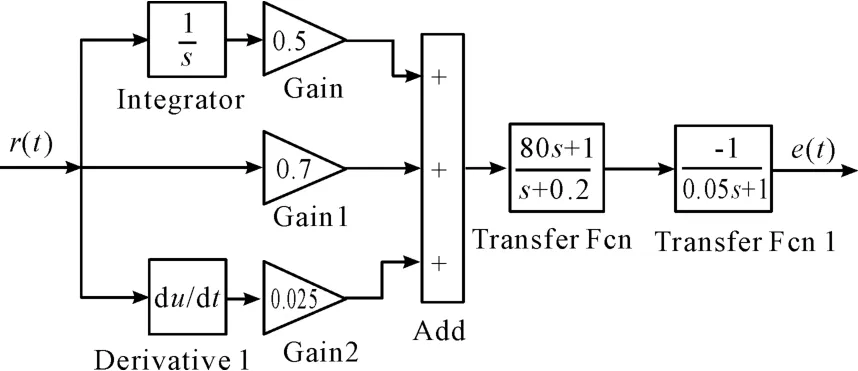
图2 控制部件和舵机模型的Simulink仿真框图
2 随机误差建模与处理
2.1 随机误差因素分析
在导弹实际飞行过程中,受到的各种干扰因素都是随机的,如武器平台误差、发动机推力偏心、初始扰动、弹体质量分布不对称、导引系统和控制系统各元部件参数误差等。本文所考虑的随机误差因素及其最大变化范围是在参考文献[6-8]的基础上,通过大量仿真试验归纳得到的,具体如表1所示。若随机误差超出其最大变化范围,则会导致导弹的导控性能骤减,甚至不能命中目标。
2.2 随机误差因素建模
一般情况下,随机误差变量服从正态分布,而误差相位服从均匀分布,即随机变量X~N( μ,δ2)。服从正态分布随机误差变量的数学表达式为
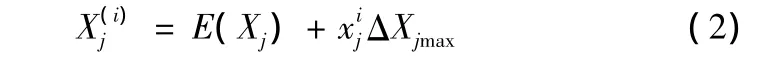
式中:j为随机误差分量序号;i为第i次抽样计算;E(Xj)为第j个随机误差分量的数学期望;ΔXjmax为第j个随机误差分量分布区间的一半(3δ);xj为正态分布的随机数,X~N(0,1/3)。
2.3 随机误差因素处理
对于表1中1~24的误差因素,通过调整导弹模型中各对应参数的仿真初始值来实现,即用randn函数在原仿真初始值上分别加上相应不同的随机误差值,得到蒙特卡洛打靶仿真的初始值。对于表1中25~31的误差因素,则用Simulink中Random Number模块所产生的随机信号,分别加到导弹模型的俯仰和偏航2个控制信号上来实现,加入随机信号的均值为0,标准差为0.001。
3 蒙特卡洛打靶的实现
计算机仿真打靶是研究导弹命中精度的一种重要手段[9]。本文采用Simulink实时仿真(RTW)的快速仿真目标功能(RSIM)来实现蒙特卡洛仿真打靶[10]。设置完成后,只需运行以下程序即可对导弹模型进行500次打靶仿真。
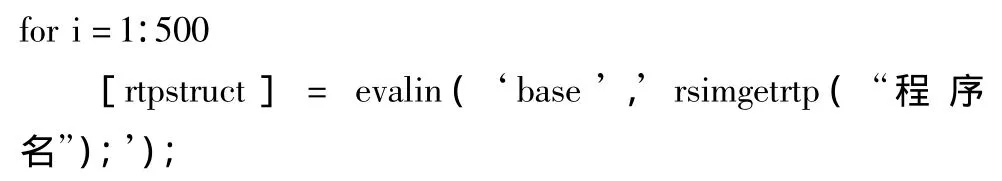
%在基本工作空间执行rsimgetrtp函数,获取Simulink模型的参数结构体。


对蒙特卡洛打靶结果进行统计,弹着点的数学期望和标准差计算公式为
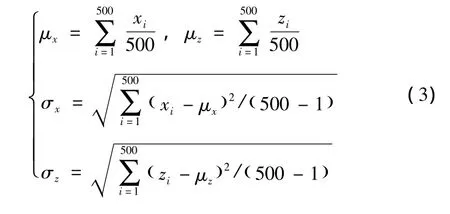
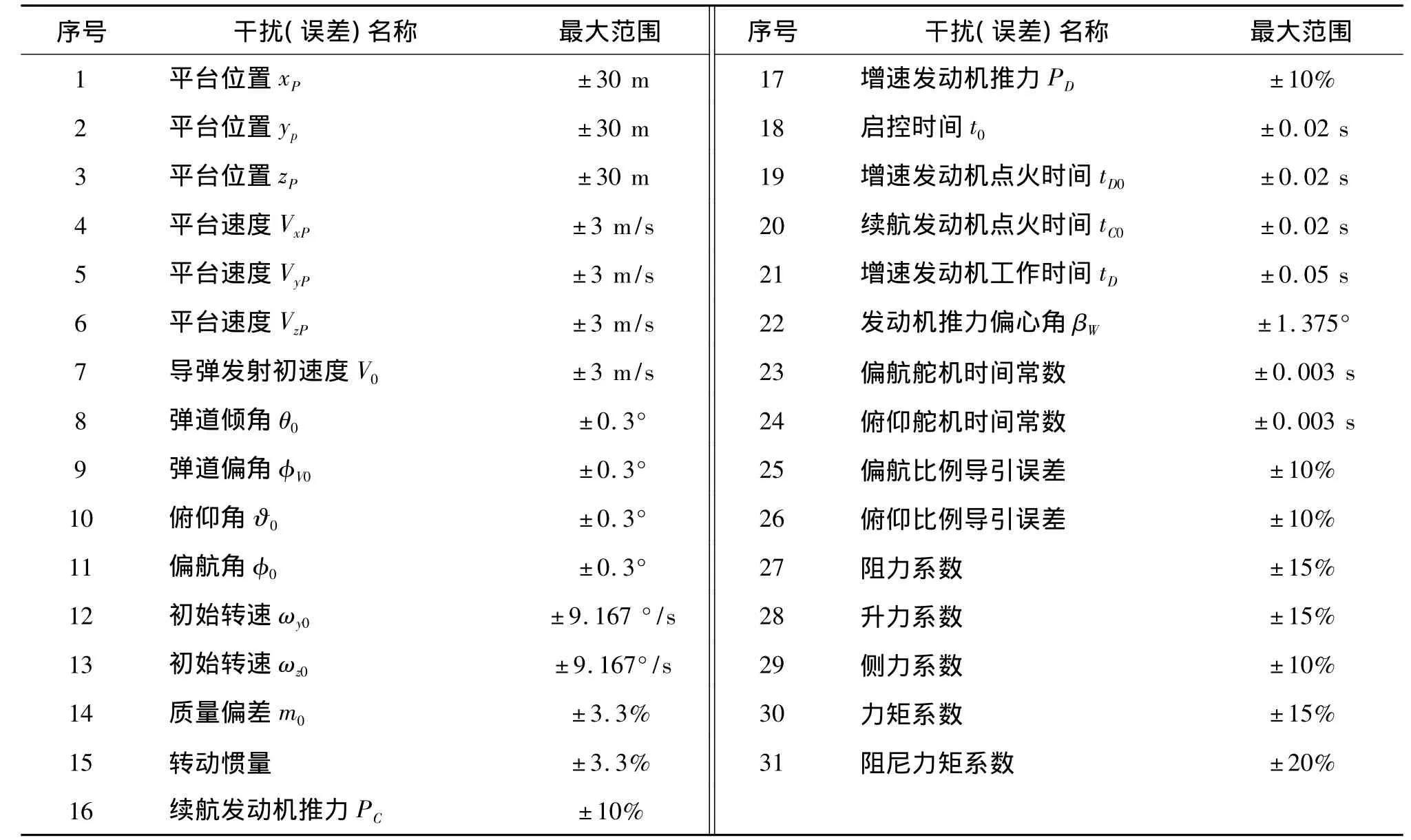
表1 随机误差变化范围
4 CEP定义及计算方法
前苏联、西方国家和我国早期都是以散布中心(平均弹着点)为圆心来定义CEP的,如《GJB102A—98弹药系统术语》中对CEP的定义为:表示射击密集度性能的指示,出现概率为50%的圆形误差范围的半径。这只能用来表示弹着点或定位精度的随机误差,即密集度。然而,要完整描述导弹射击或定位的精确度,还必须考虑弹着点或定位精度的系统误差,即准确度。《GJB6289—2008地地弹道式导弹命中精度评定方法》将CEP定义为:以目标点为圆心,弹着概率为50%的圆域半径,记为CEP。这个定义包含了精度试验的系统误差,是弹着点或定位精度系统误差和散布误差的总和。为准确描述导弹落点或制导精度,本文采用包含系统误差的CEP定义方法[11],其计算式为式(4)。
特别指出,CEP的不同定义相对应有不同的计算方法和适用条件。在实际应用中,应先根据被考核导弹的指标,明确所用CEP的定义;然后确定试验方法和数据处理方法。一定要考虑样本数据情况和应用场合,不能直接套用简化公式进行计算。

其中:ρ为样本相关系数,当存在系统误差且σx≠σz时,ρ≠0;μx,μz为样本均值;σx,σz为样本标准差;n 为样本容量。
5 算例及仿真结果分析
某微型导弹在无人机上发射,发射坐标为x=0 m,y=300 m,z=0 m,仿真初始条件如表2所示。
5.1 打击固定目标
目标位置坐标为Xt=3000 m,Yt=0 m,Zt=300 m,进行500次模拟打靶试验,弹着点在Oxz平面内的分布情况如图3所示。

表2 仿真初始参数
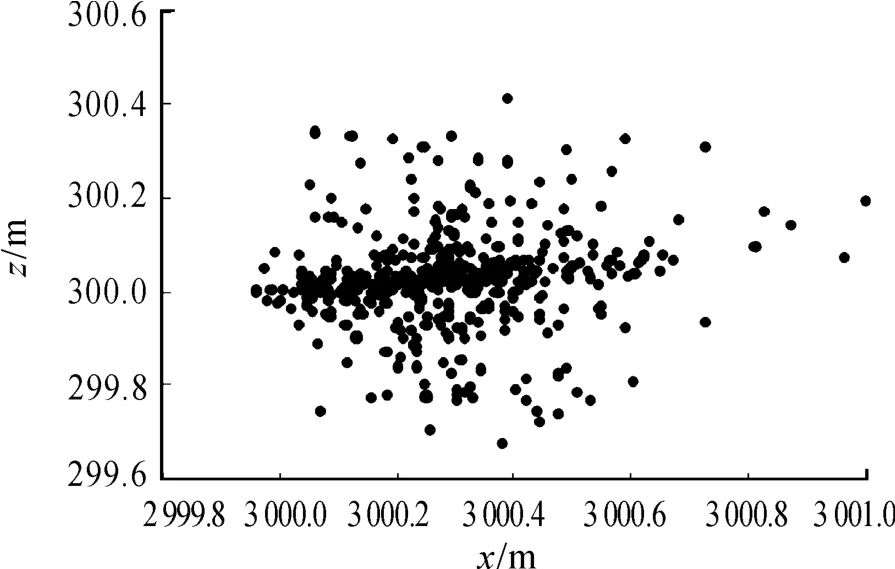
图3 弹着点在Oxz平面内的分布情况
打击固定目标弹着点显著水平α=0.05的数学统计如表3所示,导弹的CEP=0.2985 m。
5.2 打击运动目标
假设装甲车初始位置坐标为Xt=3000 m,Yt=2 m,Zt=0 m,速度为 Vx=22.22 m/s,Vy=0 m/s,Vz=-15sin(0.3t)m/s,进行500次模拟打靶试验,导弹落地时弹目在Oxz平面内的分布情况如图4所示,脱靶量分布图如图5所示。
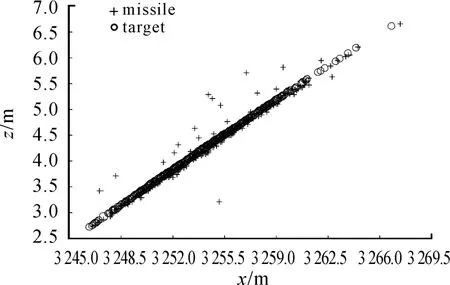
图4 导弹落地时弹目在Oxz平面内的分布情况
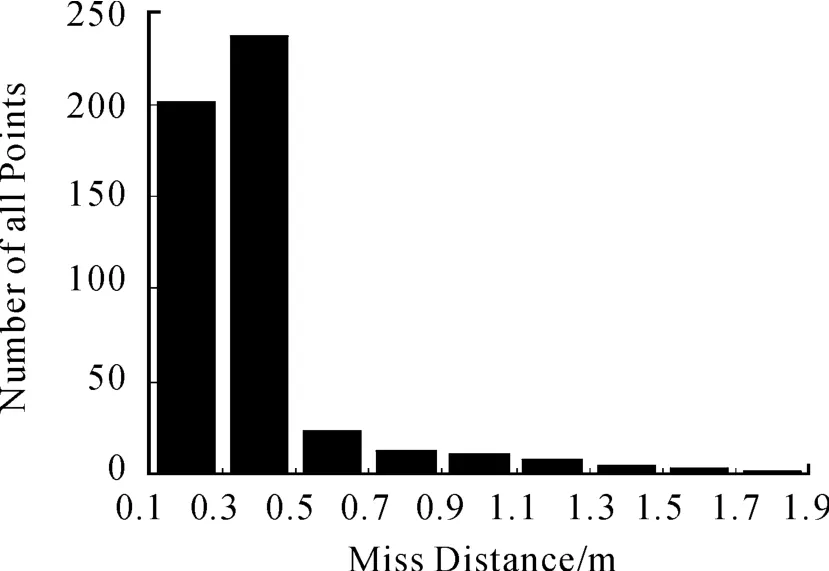
图5 脱靶量分布
打击运动目标弹着点显著水平α=0.05的数学统计如表4所示。

表3 固定目标弹着点数学统计表

表4 运动目标弹着点数学统计表
6 结束语
本文从实际应用出发,建立了受多种随机误差因素影响的某非旋转空地微型导弹六自由度精度分析仿真模型。仿真结果表明,该导弹打击固定目标的制导精度较高,CEP=0.2985 m;打击运动目标的脱靶量最大为1.9 m,最小为0.1 m,精度也较高;若以1.1 m为有效杀伤半径,则导弹的命中概率为96.6%。这不仅验证了导弹仿真模型的准确性,还可为该弹的研发或作战训练提供理论指导,具有一定的参考价值。
[1]罗俏,张伟,李伟.微型导弹蒙特卡洛打靶仿真研究[J].飞行力学,2013,31(3):265-268.
[2]王少峰,章惠军,阎杰.空空导弹精度分析的数字仿真方法研究[J].弹箭与制导学报,2006,26(1):695-697.
[3]符文星,朱苏朋,陈士橹.空地导弹制导精度分析及仿真[J].弹箭与制导学报,2005,25(4):833-835.
[4]姚志敏,冯振声,马立元.地地弹道导弹射击精度评估与分析[J].火力与指挥控制,2000,25(4):60-61.
[5]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2012.
[6]袁子怀,钱杏芳.有控飞行力学与计算机仿真[M].北京:国防工业出版社,2001.
[7]徐敬青,齐杏林,王军波,等.推力偏心对精确制导火箭弹的弹道影响仿真[J].弹箭与制导学报,2012,32(2):127-130.
[8]王华,徐军,张芸香.基于Matlab的弹道蒙特卡洛仿真研究[J].弹箭与制导学报,2005,25(1):181-183.
[9]Hanson J M,Beard B B.Applying Monte Carlo simulation to launch vehicle design and requirements verification[J].Journal of Spacecraft and Rockets,2012,49(1):136-144.
[10]耿斌斌,杨涤.快速仿真方法在蒙特卡洛打靶中的应用[J].飞行力学,2005,23(4):74-77.
[11]张乐,李武周,巨养锋,等.基于圆概率误差的定位精度评定办法[J].指挥控制与仿真,2013,35(1):111-114.

