悬臂式簧片哨发声特征的研究
许昊,吴胜举,邸惠芳,施秋华
悬臂式簧片哨发声特征的研究
许昊1,2,吴胜举2,3,邸惠芳2,施秋华1
(1. 湖北省计量测试技术研究院,湖北武汉430223;2. 陕西师范大学物理学与信息技术学院,陕西西安710119; 3. 陕西省超声重点实验室,陕西西安710119)
采用计算流体动力学软件Fluent和前处理软件Gambit,分析射流速度在簧片附近压力、湍流强度等参数的影响。在实验室用水听器、信号分析系统等测量设备对不同规格的簧片在工作过程中的声信号进行采集、分析。结果表明,实验中所用的簧片在一定工作条件下都会产生相应的谐频信号,且射流具有一定的脉动性。由于射流中包含了较为丰富的频率成分,其中包括了簧片的固有频率和谐频相一致的频率,从而使簧片共振发声并产生谐频。
簧片哨;射流;谐频;数值计算;频谱
0 引言
流体动力式声波发生器,以高速流体(气体和液体)冲击楔形板、簧片或共振腔而产生声音,在已有的文献中,将此界定为边棱音(edge-tone)。目前,关于边棱音的研究大多集中在空气中,由于气体相对液体来说密度小、黏滞力低,簧片发声所需的条件很容易达到,而且在低雷诺数下既不要求压缩性,也不需要湍流模型,所以在实验的观测和模拟中相对较为简单。
与气体边棱音发声不同,簧片哨是以液体作为动力源形成的射流液片冲击一定厚度的簧片,发声是工作在高雷诺数的湍流状态下。由于射流的流体动力学是一个非常复杂的问题,且射流与簧片耦合发声的物理模型尚不清楚,对其数学处理也非常困难,已有的研究工作大都以实验为基础,且实验难度较以往研究更加复杂。即使实验中施加定常的边界条件,速度和其他流动量也是以随机和混沌的方式变化[1],致使发声特征和机理的研究一直没有取得显著的进展。
簧片哨的主要结构由喷嘴和正对于喷嘴放置的楔形物组成,传统上称边棱(见图1)。此结构是簧片哨发声的中心部件。喷口加以一定速度的射流,在某些情况下会发出可闻声。
本文利用计算流体动力学软件(Computational Fluid Dynamics, CFD)进行模拟,施加定常的边界条件,所以在模拟过程中将射流看为定常湍流[2]。采用标准模型,通过改变喷嘴的出口速度,研究喷嘴的速度对簧片的作用,并对其流场进行数值计算,结合实验中的数据采集设备对发声频率进行测量,并对时域信号进行分析,研究其发声的特征,继而为进一步研究发声机理奠定基础。
1 理论模型
,(1)
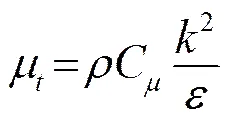
(3)
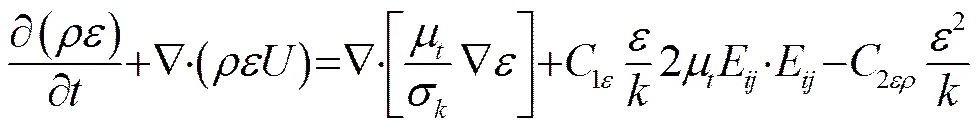
式中,G是由于平均速度梯度引起的湍动能的产生项,1、2为无量纲常数,和分别是与湍动能和耗散率对应的Prandtl数。、的输运方程是(或)的变化率加上对流输运的(或)等于扩散输运的(或)加上(或)生成率再加上(或)的减少率。
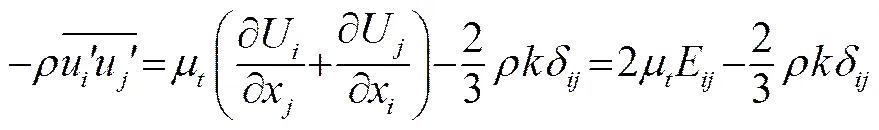
,,(6)
式中,为流速,为壁粗糙参数。
2 数值计算
通过改变射流速度,观察其喷嘴和簧片之间的速度变化、湍流强度分布来研究射流速度对簧片发声的影响。建立几何模型如图2所示[4]。
入口处的边界定义为压力入口,喷嘴边界定义为壁面,出口处各个边界定义为压力出口,压力设为静压。
3 模拟结果及分析
以喷嘴长度为10mm、厚度为2mm、喷嘴到簧片尖端的距离为10 mm的簧片哨为例,并设入口压力为0.2 MPa。在喷口和簧片之间10 mm的直线距离以及簧片边棱的两侧设置监测线,得到监测线上的湍流动能、压力等的分布,图3中a是喷口到簧片间的线,b、c分别是簧片边棱两侧的监测线。图4、图5分别是某瞬时的湍流动能及压力的分布图[7]。
图6是在四个不同时刻监测线段a,b和c上切向速度的分布。从图6可以明显地看到射流以及作用到簧片上的速度发生了明显的抖动[8]。尤其是在簧片尖端和射流的交点处,即作用在簧片尖端上的流速发生的变化最为明显。监测线段a的速度变化呈现出明显的脉动特性,由线段b、c可以看到簧片两侧的速度也时大时小,所以作用在簧片两侧的压力的不同使簧片产生振动。从时间的演变中可以看出射流速度方向具有一定的交变性,簧片哨在工作时喷射的射流具有一定规律的脉动性。
4 实验结果及分析
为了验证数值计算具有一定的可靠性,在现有的实验室条件下进行实验验证。实验装置主要由涡旋泵、流量计、压力表、水槽组成,信号检测装置由测量放大器、音频分析系统、数字示波器等组成,水听器型号为B&K8103型,工作频率范围为0.1 Hz~180 kHz,测量位置在簧片正上方10 cm处,测量传声器型号为B&K4191型,工作频率范围为3 Hz~40 kHz,测量位置为水听器正上方100 cm处。装置系统框图见图7。
簧片角度为30°,喷嘴尺寸为10 mm×2 mm ×12 mm,喷嘴到簧片的距离为10 mm,液体的工作压力为0.5 MPa,测量不同长度的矩形簧片发声频率的规律及变化。图8为未加簧片时的噪声频谱图。
(a)
(b)
(c)
(d)
图6 监测线段不同时刻的相对切向速度
Fig.6 The velocity distribution at different times on monitoring line
在未加簧片时由于高速的射流产生了宽频噪声信号,该信号可近似为本底噪声。但是频谱特性始终在一定的范围内变化,这也能说明射流具有一定的脉动信号特征,包含了丰富的频率成分。
安装47 mm×34 mm×2 mm的簧片,固定簧片和喷嘴的距离,保持射流速度不变,通过软件分析得到如图9所示的频域图。
分析对比发现簧片的主要发声信号在526.50、1056.57和1586.30 Hz。通过比较还可以发现,其三个共振频率之间满足下列关系:若以第一个共振频率526.50 Hz为基频[9],三个共振频率与基频之间满足倍1: 2: 3的倍数关系。再将56 mm×34 mm×2 mm的簧片安装后测得频谱,如图10所示。
通过对图10的观察可以发现尺寸为56 mm×34 mm×2 mm的矩形簧片与尺寸和47 mm×34 mm×2 mm的矩形簧片有相似的规律,前三个共振频率分别为350.00、703.00和1056.00 Hz;共振频率之间亦满足1: 2: 3的倍数关系[10]。
同样在图11中对于尺寸为65mm×34mm×2mm的矩形簧片与前两种簧片的发声规律一致,前三个共振频率分别为:254.80、496.70和753.00 Hz,共振频率仍满足上述关系。
对于1 mm厚度的簧片,通过实验仍可得到相似规律。在不改变外界工作环境的条件下,尺寸为47mm×34mm×1mm的簧片,前三个共振频率分别为215.00、430.00、635.00 Hz;尺寸为56mm×34mm×1mm的矩形簧片,前三个共振频率分别为156.0、315.0和465.0 Hz;尺寸为65mm×34mm×1mm的矩形簧,前三个共振频率分别为:106.00、220.00和315.00 Hz,同样1.5 mm厚度的簧片也有类似规律。
改变工作压力后,簧片依然有此规律。当工作压力固定为数值计算设定的0.2 MPa时,尺寸为47 mm×34 mm×1.5 mm的簧片,前三个共振频率分别为390.00、785.00、1105.00 Hz,尺寸为56 mm×34 mm×1.5 mm的簧片,前三个共振频率分别为265.0、525.0和790.0 Hz,尺寸为65 mm×34 mm×1.5 mm的簧片,前三个共振频率分别为:179.00、370.00和510.00 Hz。
在固定工作条件的情况下,同种类型的簧片厚度和宽度一定时,随着簧片长度的增大,其固有频率逐渐降低。并且不同类型簧片的振动过程中皆产生了泛音即谐频,这种现象也是普遍的。出现谐频的原因是簧片受到外界包含有簧片固有频率的激发力而导致簧片共振,同时产生了振动节点。此时由于外界的激发频率是宽带信号,激发了以此节点为定点的振动状态,从而产生谐频。如果节点在簧片的1/2处,那么谐频就是簧片基频的2倍,如果节点在簧片的1/3处,那么谐频就是基频的3倍。这也同时说明了此时簧片的振动模态并不是单一的,具有一定的复杂性。
用频谱分析设备分析射流作用在簧片的信号时,发现频谱中包含了随机且丰富的宽频信号。相同工作条件下,不同规格的簧片发声且产生谐频,证明了射流包含了较丰富的频率成分,具有一定的脉动特性,从而激发簧片振动产生不同频率的声信号,在模拟中也观察到了射流的脉动特性,这也能进一步说明模拟结果是可靠的。
5 结语
实验结果表明在不改变工作条件下喷嘴的射流速度呈现了脉动性的典型特征,射流作用到簧片上的信号也是丰富的宽频信号。喷嘴以一定压力喷出射流,射流冲击到簧片上使得簧片共振发声。在工作条件相同的情况下,不同长度及厚度的簧片在一定的频率发声,且都会有谐频出现,谐频的产生也是由射流的脉动性和簧片的固有频率共同导致的。分析发现射流中包含丰富的频率,其中包括了簧片的固有频率和二次、三次谐频相一致的频率成分,从而证明簧片发生了共振并同时产生二次、三次谐波。
[1] 李万平. 计算流体力学[M]. 武汉: 华中科技大学出版社, 2004, 1-9.
LI Wanping. Computational fluid mechanics[M]. Wuhan: Hua Zhong University of Science and Technology Press, 2004, 1-9.
[2] 张兆顺. 流体力学[M]. 北京: 清华大学出版社, 2006, 9.
ZHANG Zhaoshun. Fluid dynamics[M]. Beijing: Tsinghua University Press, 2006, 9.
[3] 王福军. 计算流体动力学分析——CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004, 9.
WANG Fujun. Computational fluid dynamics-CFD software principle and application[M]. Beijing: Tsinghua University Press, 2004, 9.
[4] Hokeun kang. On Implementation of the Finite Difference Lattice Boltzmann Method with Internal Degree of Freedom to Edge tone [J]. Journal of Mechanical Science and Technology, 2005, 19(11): 2032-2039.
[5] Devillers J F, Coutier-D O. Influence of the nature of the gas in the edge-tone phenomenon[J]. Journal of Fluids and Structures, 2005, 21(2): 133-149.
[6] 张捷迁. 真实流体力学[M].北京: 清华大学出版社, 1986, 11.
ZHANG Jieqian. Real fluid mechanics[M]. Beijing: Tsinghua University Press, 1986, 11.
[7] 江帆, 黄鹏. Fluent高级应用与实例分析[M]. 北京: 清华大学出版社, 2008, 1.
JIANG Fan, HUANG Peng. Fluent advanced application and example analysis[M]. Beijing: Tsinghua University Press, 2008, 1.
[8] 许昊, 吴胜举, 孙军涛. 射流对簧片哨发声的影响[J]. 陕西师范大学学报: 自然科学版, 2012(5): 39-42.
XU Hao, WU Shengju, SUN Juntao. The jet’sinfluence on the edge tone in reed whistle[J]. Journal of Shaanxi Normal University: Natural Science Edition, 2012(5): 39-42.
[9] 许昊, 吴胜举, 孙军涛. 簧片振动模态的有限元分析[J]. 声学技术, 2011, 30(5): 48-52.
XU Hao, WU Shengju, SUN Juntao. Finite element analysis of vibration modes of Reed-Whistle[J].Technical Acoustics. 2011,30(5): 48-52.
[10] 中国科学技术情报研究所编辑. 超声译丛第一集[M]. 北京: 中国科学技术情报研究所, 1960: 184-199.
Science and technology information institute of China edit. The first set of ultrasonic translations[M]. Beijing: Science and Technology Information Institute of China, 1960: 184-199.
Research on sound characteristics of cantilever reed whistle
XU Hao1,2, WU Sheng-ju2,3, DI Hui-fang2, SHI QIU-hua1
(1.Hubei Institute of measurement and testing technology,Wuhan 430223, Hubei, China;2.Applied Acoustic Institute, Shannxi Normal University,Xi´an 710119, Shannxi, China;3.Key Laboratory of Ultraphonics, Shannxi Province,Xi´an710119, Shannxi, China)
In this paper the computational fluid dynamics software Fluent and the former processing software Gambit are used to analyze the effects of jet velocity on the pressure, turbulence intensity and other parameters near the reed. In laboratory the hydrophone and measuring equipment are applied to collecting and analysing the acoustic signal of the reed with different specifications in the working process. Results show that the reed under certain working conditions produce corresponding harmonic signals, and the jet with definite pulsation. Because the jet contains relatively abundant frequency components, including the natural and harmonious frequencies which are in agreement with the reeds’ frequencies, making the reed vibrated and generated harmonic signals.
reed whistle; the jet; Harmonic frequency; numerical calculation;frequency spectrum
TB533
A
1000-3630(2015)-02-0147-05
10.16300/j.cnki.1000-3630.2015.02.009
2014-01-22;
2014-04-20
国家自然科学基金资助项目(11074158)。
许昊(1986-), 男, 安徽金寨人, 硕士, 研究方向为声学测量、噪声控制处理。
吴胜举, E-mail: wushju@snnu.edu.cn

