运用传递函数模型预测儿童医院日门诊量

钱丽萍，马亚娜，孙宏鹏（1.苏州大学附属儿童医院，江苏省苏州市15003；.苏州大学医学部公共卫生学院，江苏省苏州市15006）

◁门急诊管理▷

运用传递函数模型预测儿童医院日门诊量

钱丽萍1，2，马亚娜2*，孙宏鹏2
（1.苏州大学附属儿童医院，江苏省苏州市215003；2.苏州大学医学部公共卫生学院，江苏省苏州市215006）

目的建立传递函数模型，预测儿童医院日门诊量，并找出天气相关指标和儿童医院门诊量的相关性，为门诊管理决策提供依据。方法应用SPSS17.1软件，利用2014年前41周日门诊量的数据和天气相关指标建立函数传递模型，预测下一周的日门诊量，计算误差率。结果日门诊总量预测模型的表达式为ARIMA（0，1，2）（0，1，1）7，与最高温度、最低温度显著相关，平均误差率为4.32%。结论传递函数模型能准确预测儿童医院日门诊量，其能为医院门诊管理提供准确的预测数据。

传递函数模型；预测；日门诊量；儿童医院；天气指标

【DOI编码】 10.3969/j.issn.1672-4232.2015.06.024

对医院主要业务数据进行科学的趋势分析与预测是实行医院科学管理的主要手段之一［1-3］。门诊是医疗工作的一个重要组成部分，是医院对外服务的窗口，准确预测医院的门诊量是做好医院门诊管理工作的重要前提。因儿童的生理特点导致儿童对外界环境的调节不如成人，在传染病较易传播的春季、高温的暑期、秋冬季交界的时节，各省市儿童医院经常被曝人满为患，因此，科学、准确预测儿童医院门诊量，有利于医院更好地统筹安排门诊资源，提高门诊管理水平，保障儿童的医疗安全。另外，儿童常见病的发病是否和天气因素有关联，也是值得探讨的话题。

自回归移动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）是最重要的时间序列分析，适用于短期预测。乘积季节求和自回归移动平均模型（ARIMA product seasonal model，ARIMAS）是针对季节时间序列提出的一种预测模型，是随机季节模型与自回归移动平均模型的结合，可视为ARIMA模型的一种特殊形式，其表达式为ARIMA（p，d，q）（P，D，Q）s。传递函数—噪声模型（transfer functionnoise model），简称传递函数模型，是多元时间序列分析中的一种，属多变量时间序列模型。该模型可以看作是ARIMA模型和多元回归模型的结合。ARIMA方法预测医院的总门诊量或者专科门诊量，并与实际门诊量相比较，取得了较好的预测效果［4-6］。有学者研究过，5岁以下儿童死亡率预测、传染病发病率预测等，加入常见的外部影响因素作为变量，能更准确地预测研究对象［7-8］。

本研究通过传递函数模型预测苏州大学附属儿童医院的日门诊量，通过短期预测得到连续数日的值，结合医院实际管理工作的需要，将预测的数据选择为下一周7天的门诊量。

1　资料

该研究中门诊量数据来源于苏州大学附属儿童医院的医院信息系统，包括每日内科普通门诊量、内科专〗家门诊量、外科普通门诊量、外科专家门诊量、内科急诊量、外科急诊量，不包含儿童保健科、眼科、五官科、口腔科和皮肤科。天气数据均来自于天气后报网站，包括每日空气质量指数、最高温度、最低温度。空气质量指数为每日空气质量指数预报的平均值，最高温度和最低温度均使用苏州地区天气预报数据，并使用摄氏度为单位。

2　方法

由图1，分析2013年12月1日（第1周）到2014 年11月22日（第51周）的数据发现，日门诊量具有一定的波动性，从12月1日开始数据有规律地波动，并有一定的上升趋势，在1月底突然下降，随后进入低谷又逐渐反弹。因为苏州外来人口和户籍人口持平，春节期间返乡人口影响了就诊目标人群，所以建模使用数据的时间段为2014年2月2日（第10周第1天）到11月22日（第51周第7天），用年初前41周共287天的数据预测下一周7天的每日门诊量。在预测过程中，ARIMAS模型中加入天气相关指标，即空气质量指标、每日最高温度和每日最低温度，判断预测的准确性以及天气相关指标与门诊量的相关性。

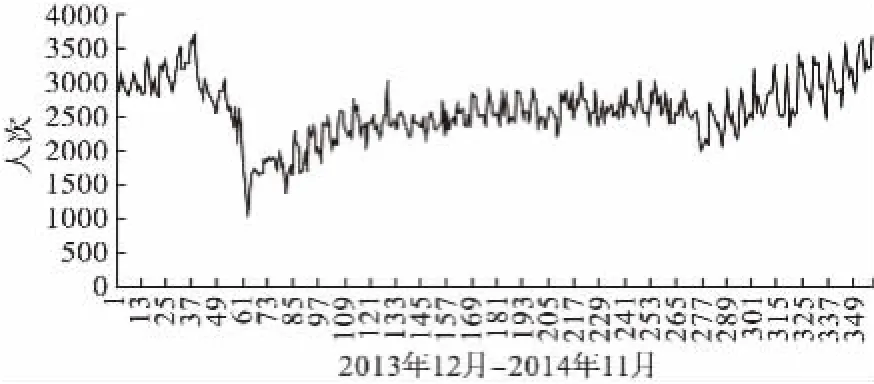
图1　2013年12月至2014年11月日门诊量分析

传递函数模型预测日门诊量的过程如下：

（1）模型的识别。通过分析2014年2月2日到11 月15日每日门诊总量的数据，结果显示符合时间序列。根据SPSS17.1软件相关功能的运行，门诊总量的自相关函数图和偏自相关函数图（见图2），时间序列的自相关函数有衰减的特征，而偏自相关函数迅速衰减趋向于0，由此可以判断数据属于非平稳系列，因此要进行差分。

（2）模型参数估计。在SPSS软件中，利用预测功能，对模型的参数经过不断地估计、尝试和调整，在d= 1，D=1，q=2，Q=1，p=0，P=0时，找到合适的拟合模型。

（3）模型的检验。此时Stationary R2=0.65（Stationary R2＞0.20），Ljung-Box Q（18）检验P=0.583，从残差自相关函数图和偏自相关函数图上可以看出，残差趋向于0但不等于0，落在一个有效的区间内（见图3），说明该模型残差为白噪声平衡，模型统计意义较好。因此确定该模型为ARIMA（0，1，2）（0，1，1）7。同时加入空气质量指数、最高温度和最低温度三个指标作为输入变量，最高温度和最低温度在模型中具有统计学意义（P＜0.05），说明最高温度和最低温度作为有效输入变量参与了模型的拟合。

（4）检验误差率。利用预测的每日门诊量和实际值作比较，计算误差率，检验模型的准确性。

3　结果

日门诊总量预测模型的表达式为ARIMA（0，1，2）（0，1，1）7，与最高温度、最低温度显著相关。该预测模型较好地拟合了前41周的数据，并预测下一周7天的日门诊量，拟合值落在置信区间内，预测的拟合图详见图4。

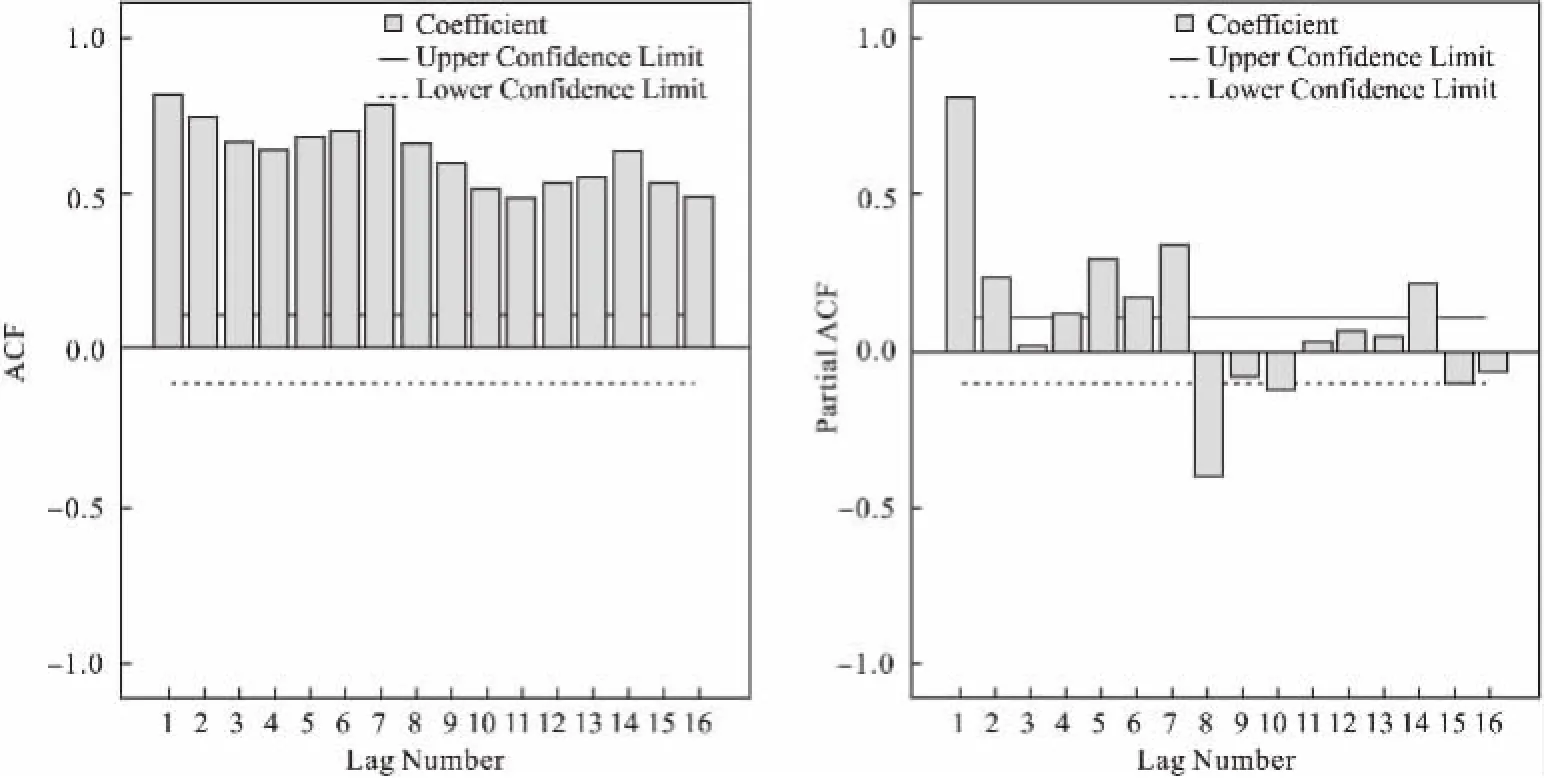
图2　差分前自相关函数图和偏自相关函数图

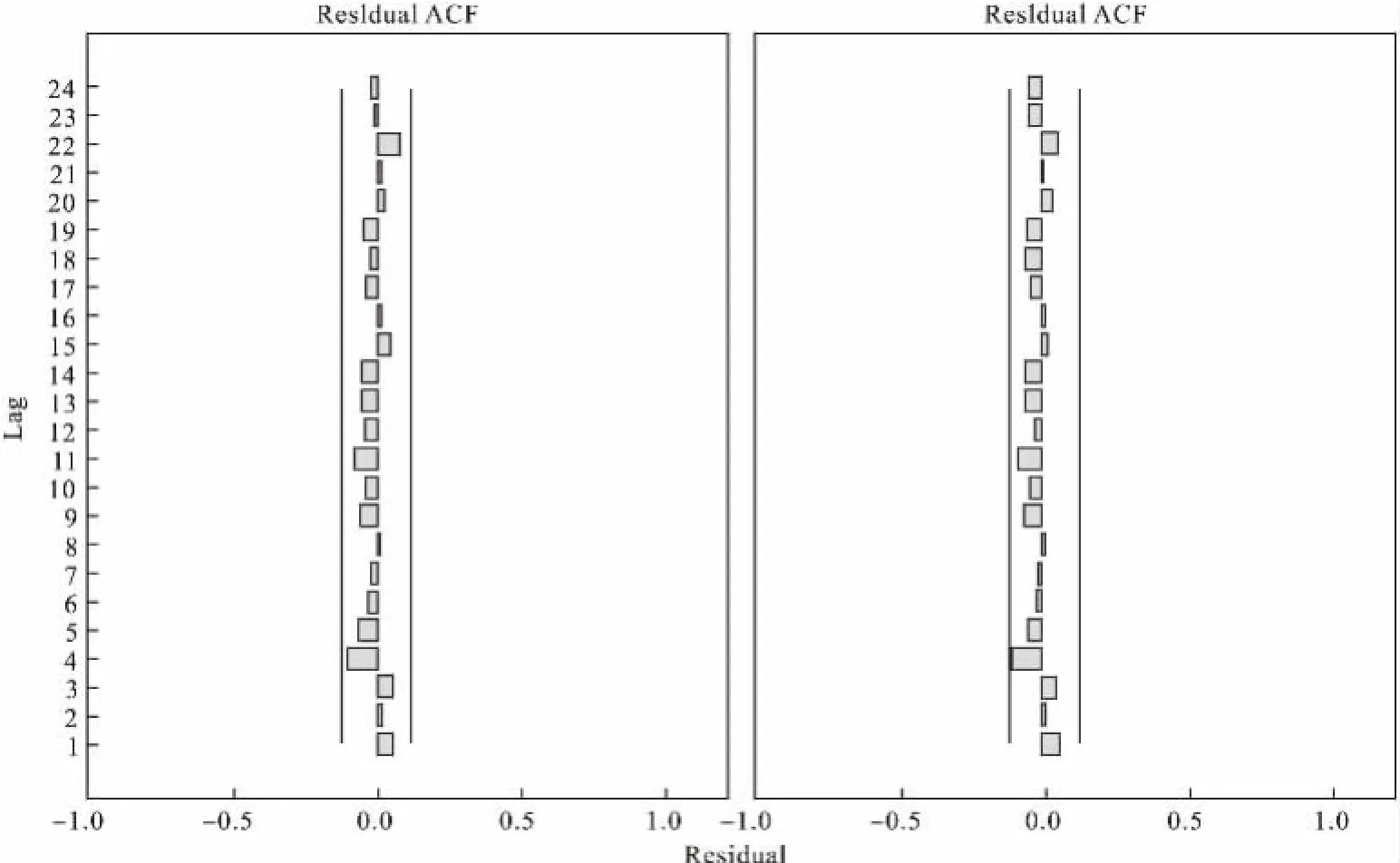
图3　残差自相关函数和偏自相关函数图

图4　日门诊量预测拟合

ARIMAS预测结果准确性用相对误差率来判断，计算公式如下：。11月16日至11月22日门诊量预测的误差率计算结果见表1。

表1　2014年11月16—22日门诊量预测误差

4　讨论

4.1模型预测的准确性

该预测中，利用儿童医院2014年门诊数据，传递函数模型能够准确地拟合各门诊人次的季节波动及趋势特征，找出历史数据随时间发展的变化规律，建立合适的模型。预测的相对误差率最大为7.29%，最小为1.36%，平均误差率为4.32%，预测效果较好。天气相关指标作为多元变量，每日最高温度和每日最低温度与日门诊量显著相关，说明两变量参与了模型构建，使模型拟合得更加准确。因此，通过传递函数模型，加入天气相关指标作为多元输入变量，预测儿童医院门诊量是可行的，并能得到较准确的预测值。

4.2影响门诊量预测的因素

从某种意义上说，影响门诊量的因素也可能是影响门诊量预测的因素。影响门诊量的因素是多方面的：（1）医院的因素，如医院的技术力量、服务质量等；（2）病人的因素，如医保类型、疾病轻重等；（3）医保政策、自然环境因素等。这些因素错综复杂，难以量化。天气相关指标在日常生活中较容易获取，而且属于量化指标，能参与模型的构建。该研究证实温度和儿童医院门诊量有显著相关，这为其他专科门诊或某疾病门诊量预测提供参考依据。有学者研究过2003年因“非典”原因导致门诊量预测失灵［9］，所以在建立模型的时候尽量选择受外部影响小的数据。此研究预测时使用了2014年2月2日后的数据，以便找到拟合、预测更准确的模型。

4.3预测日门诊量对医院日常管理的指导意义

运用传递函数的短期预测功能可得到下一日门诊量或下一周的门诊量，对实际管理工作具有重要价值。门急诊的管理是反映医院管理水平高低的重要指标之一，门诊量的预测能为门诊医护人员的配置提供可靠依据，对医院合理安排人、财、物等资源以提高经济效益和社会效益有重要意义。儿童疾病以急性病居多，在日常工作中，常因患儿的门诊等候时间过长而出现各种意外情况甚至是医疗纠纷，病人对医院的满意度也会降低，准确地预测门诊量是医院短期内调配人力资源的重要依据。只有在准确预测门诊量后，才能确保医务人员承担合理的工作量，如果医护人员配置相对较少，导致医护人员工作量负荷太大，给医护人员身心造成不利影响；反之则造成人力资源浪费。

5　不足和局限

由于使用数学模型预测，得到的只是理论值，难免存在局限性和不完备性。由于儿童疾病本身的复杂性、多样性及研究的广泛性，致使该研究工作尚有一些不成熟的地方，有待进一步的深入研究。对门诊量的预测只是科学的估计，较难量化各影响因素的影响程度，因此对已建立的模型，必须引入新的观察数据修正或重新拟合。如果我国或者局部地区实行严格的分级诊疗制度和预约制度，该模型则不再适用。

［1］张珊珊.中医医院门诊工作量的季节性分析及预测研究［J］.数理医药学杂志，2013，26（6）：675-678.

［2］徐永强，周静.ARIMA（p，d，q）模型在不同地区来源门诊量预测中的应用［J］.中国医院统计，2009，16（3）：202-206.

［3］孔超.基于灰色预测模型的门诊量预测：以上海市浦东新区门诊总量为例［J］.中国卫生资源，2008，11（6）：267-268.

［4］李运明，吴凡，郑驰，等.某三甲综合医院门诊量ARIMA预测分析［J］.中国病案，2014，（8）：53-55.

［5］曾允萱，蔡旭娜.基于时间序列分析法的医院月门诊量预测模型［J］.中国医院统计，2009，（4）：312-315.

［6］耿娟.ARIMA模型在医院门诊量预测中的应用［J］.中国卫生统计，2014，31（4）：643-645.

［7］刘元元，朱军.传递函数模型在我国5岁以下儿童死亡率预测中的应用［J］.中华妇幼临床医学杂志：电子版，2008，4（2）：25 -27.

［8］姜立坤，赵晶，李岩，等.利用传递函数模型对麻疹发病趋势的预测研究［J］.中国初级卫生保健，2012，（8）：69-71.

［9］武权，王海威，魏星.两种模型在医院门诊量预测中的应用［J］.西南国防医药，2010，20（5）：553-554.

修回日期：2015-10-08（编辑曹晓芸）

Prediction of Daily Outpatient Visits to Children's Hospital with Transfer Function Model

QIAN Li-ping1，2，MA Ya-na2*，SUN Hong-peng2
（1.Children's Hospital Affiliated to Soochow University，Suzhou，Jiangsu 215003，China；2.School of Public Health，Medical College of Soochow University，Suzhou，Jiangsu 215006，China）

Objective：The construction of transfer function model can be helpful in predicting daily outpatient visits to children's hospitals，discovering the correlation between weather indexes and the daily outpatient visits to children's hospitals，and providing the base for making strategies of outpatient management.Method：Error rate of predicting outpatient visits the next week can be calculated with SPSS17.1 software，data of daily outpatient visits in 41 weeks before 2014 and the construction of transfer function model with indexes correlated with weather.Result：The formula for predicting daily outpatient visits is ARIMA（0，1，2）（0，1，1），which relates closely with the highest temperature and the lowest temperature.And the average error rate is 4.32%.Conclusion：Transfer function model can correctly predict daily outpatient visits，which can provide correct prediction data for outpatient management of hospitals.

transfer function model；prediction；daily outpatient visit；children's hospital；weather index

R197

A

1672-4232（2015）06-0070-04

马亚娜（1969-），女，博士，副教授；研究方向：医院管理、卫生事业管理。

2015-08-07